Journal of Research and Development
Open Access

Mini-Review on an Entropy-based Measure of Dependence between Two Groups of Random Variables

Nan L. Kong^{* *}Correspondence: Nan L. Kong, Independent Researcher, New Jersey, United States of America, Email:

Author info »

Introduction

In this mini-review, first we introduce the entropy and Information graphical representation to help us understand K-dependence coefficient. Next, we introduce the concept of measure followed by a briefly discussion on K-dependence coefficient additive structure together with several other measures, such as coefficient of determination, entropy and probability. Finally, we introduce some ideas to extend K-dependence coefficient.

Understanding K-Dependence Coefficient

K-dependence coefficient is defined from entropy and mutual information

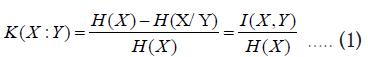
Where,

H(X) is the entropy of X,

H(X/Y) is the conditional entropy of X given Y, and

I(X,Y) is the mutual information across X and Y.

By the equation 1, K-dependence coefficient K(X;Y) is defined with the ratio of mutual information across X and Y over the entropy of X. Roughly, the mutual information and entropy can be graphically represented below:

K(X:Y) defined by the ratio of H(X) over I(X,Y) as shown in shaded area in Figure 1 measures the degree of X dependence on Y. Also, in Figure 1, it is obvious that

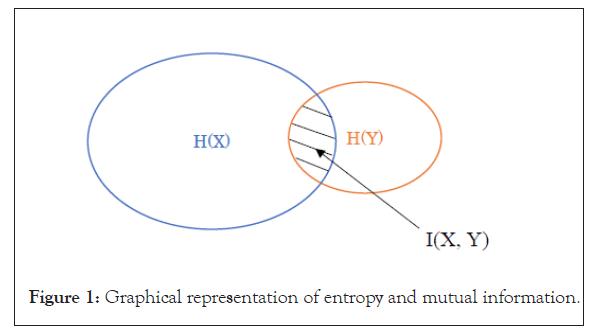
Figure 1: Graphical representation of entropy and mutual information.

0 ≤ K(X :Y) ≤1 …. (2)

The equations 1 and 2 show that K(X :Y) is standardized and therefore, it is comparable with other standardized measures such as multiple correlation coefficient (R²) and linear correlation ρ (X ,Y) etc. Please be noted that it is the squared root of K(X :Y) , not K(X :Y) itself, to compare with linear correlation [1]. Also, K-dependence coefficient is asymmetric, i.e. K(X :Y) may or may not be equal to K(Y :X) while linear correlation is symmetric, i.e. ρ (X ,Y) = ρ (Y, X ) . For example, parents’ dependence on children usually is different from the children’s dependence on parents, while the correlation between parents and children is always the same as the correlation between children and parents [2]. Mathematically, it can be proved that (i) the sufficient and necessary condition for K(X :Y)=0 is that X and Y are independent; (ii) the sufficient and necessary condition for K(X :Y)=1 is that X is a function of Y, i.e. 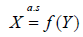. Here 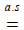means “almost equal to” (except for a zero-probability events). Below are the graphical representations of (i) and (ii):

In the case (i), Figure 2, shows no shared information across X and Y, therefore, X and Y are independent, i.e. K(X :Y)=0. On the other hand, in the case (ii), Figure 2, shows that X is part of Y in terms of their information, therefore, X is totally dependent on Y, i.e. X is a function of Y. In the general case as shown in Figure 1, K(X :Y) is between 0 and 1.

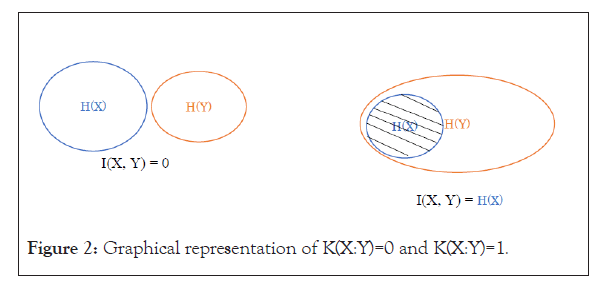
Figure 2: Graphical representation of K(X:Y)=0 and K(X:Y)=1.

K-Dependence is a Measure with Additive Structure

The concept of measure is defined in measure theory. The key concept to define a measure is called additivity [3]. In this section, we first look into several well-defined measures with the additive structure and then, we also look into the additive structure in K-dependence coefficient. We will show that K-dependence is a measure to measure the degree of dependence of one group of categorical random variables upon another group of categorical random variables [4].

In statistics, the coefficient of determination, denoted by R² or r², is the proportion of the variation in the dependent variable Y that is predictable from the predictive variables X₁,X₂,...,X_m. In case that the predictive variables X₁,X₂,...,X_m are pairwise orthogonal, then

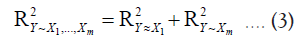
The equation 3 is called additivity showing that coefficient of determination is a measure.

In the information theory, entropy H( X₁,X₂,...,X_m ) is a measure of uncertainty for a random system or a group of random variables. In case that variables X₁,X₂,...,X_m are jointly independent, then

H( X₁,X₂,...,X_m ) = H( X₁) + H( X₂)+...+H( X_m) .... (4)

The equation 4 is called additivity showing that entropy is a measure.

Probability is a measure of randomness. In case that the events E₁,E₂,...,E_m are pairwise exclusive, then

Prob(E₁∪ E₂ ∪... ∪ E_m) = Prob(E₁) + Prob(E₂) + ... + Prob(E_m) .... (5)

The equation 5 is called additivity showing that probability is a measure.

Mathematically, it can be proved that, if all interactions among the combinations of three or more random variables out of { X,Y₁,...,Y_m } are equal to zero, then K-dependence coefficient has its additive expression:

K( X :Y₁,...,Y_m ) = K( X :Y₁ ) + ... + K( X :Y_m ) ... (6)

The equation 6 shows that K-dependence coefficient is a measure. Because coefficient of determination, entropy, probability and K-dependence coefficient are all the measures with the additive structures, they do have the similar or paralleled theoretical structures. For example, the equations 3, 4, 5 and 6 are actually the special cases of their mathematical decomposition expressions. With the additivity, a measure can correctly or precisely measure its object. Otherwise, a “measure” without additivity may cause wrong conclusion or misleading. For example, it is well known that the area of a rectangle is measured by the product of its length and width [5]. Can we measure the same rectangle by the summation of its length and width? Answer is no because product of the length and width is additive in terms of the area of a rectangle while the summation of length and width is not (but summation of length and width is additive in terms of rectangle perimeter). Any “measure” without additivity is similar or equivalent to measuring an area of a rectangle by the summation of its length and width [6].

Extension of K-Dependence Coefficient

K-dependence coefficient in the equation 1, which is defined with Entropy and Mutual Information, can be extended to include Multivariate Information. Here, Multivariate Information I (X₁,X₂) is an extension of mutual information I (X₁,X₂):

I (X₁) = H(X₁) …. (7)

I (X₁,X₂) = I (X₁) − I (X₁ / X₂ )

I (X₁,X₂,X₃) = I (X₁,X₂) − I (X₁,X₂/ X₃ )

I (X₁,X₂,...,X_n) = I (X₁,,...,X_n-1) − I (X₁,,...,X_n-1/ X_n)

Similar to the equation 1, K-dependence coefficient can be extended to measure a variable dependence on the interaction across three (or more) variables [5]:

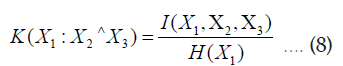
The interpretation of K (X₁ : X₂ ^ X₃) in the equation 8 is the measure of degree of X₁ dependence on the interaction associated with the combination of {X₁, X₂, X₃} i.e. I (X₁, X₂, X₃). Mathematically, the equation below can be proved:

K (X₁ : X₂ , X₃) = K (X₁ : X₂) + K (X₁ : X₃) − K (X₁ : X₂ ^ X₃) .... (9)

Obviously, K (X₁ : X₂^ X₃) = 0 is equivalent to I (X₁, X₂, X₃) = 0, i.e. no interaction associated with {X₁, X₂, X₃}. Therefore, by the equation 9, in case of no interaction associated with {X₁, X₂, X₃}, we have

K (X₁ : X₂ , X₃) = K (X₁ : X₂) + K (X₁ : X₃) .... (10)

The additivity in the equation 10 is a special case of the equation 6.

Unlike K (X₁ : X₂ , X₃) with the range between 0 and 1, K (X₁ : X₂^ X₃) can be negative:

−1 ≤ K (X₁ : X₂^ X₃) ≤1 …. (11)

Also, the following conclusions can be proved mathematically:

K (X₁ : X₂^ X₃) = 1 If and only if K (X₁ : X₂) = 1 and K (X₁ : X₃) = 1 .... (12)

K (X₁ : X₂^ X₃) = −1 If and only if K (X₁ : X₂) = 0, K (X₁ : X₃) = 0 and K (X₁ : X₂ , X₃) = 1 ... (13)

The interesting statistical structure in the equation 13 shows that, in case of K (X₁ : X₂^ X₃) = −1, the X₁ is independent from each separated individual X₂ or X₃ respectively, while X₁ is totally dependent on the interaction associated with the combination of X₁, X₂ and X₃ . In pharmaceutical industry, the equation 13 could be used to identify the interaction across different medicines. For example, we have two medicines denoted by X₂ , X_3, each individual medicine has no any impact on a target disease denoted by X₁ , i.e. K (X₁ : X₂) = 0, K (X₁ : X₃) = 0, but with the combination of these two medicines, the target disease is fully cured, i.e. K (X₁ : X₂ , X₃) = 1.

Similarly, we may look into the interactions across four or more random variables. The properties and interpretation associated with these multiple variables’ interactions would be much more complicated and meaningful. In statistics, unlike mutual relation, people pay less attention on the interactions across multiple variables. The equation 13 shows that, in some cases, the interactions can fully replace the mutual relation. Generally speaking, in a multiple variables system, the observed mutual relations could be due to the combination of mutual relation and multivariate interactions. In real world application, how to decompose or identify these mutual relations and multivariate interactions from the observed mutual relations is a challenging topic.

So far, K-dependence coefficient in the equation 1 has been extended to include multivariate information or interaction. Also, K-dependence coefficient can be extended by so-called semi-partial K-dependence coefficient:

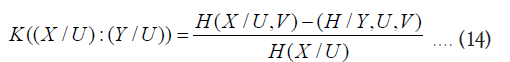
K((X | U) : (Y | V)) in the equation 14, which is called semi-partial K-dependence coefficient, is to measure the degree of (X | U) dependence on (Y | V). Here, (X | U) and (Y | V) are the random variables with the probabilities Pr(x|u) and Pr(y|v) respectively. Roughly speaking, (X | U) and (Y | V) are the random variables associated with the information of the random variables X and Y , but exclusive of the information of the random variables U and V respectively. In the real world business, how to apply and interpret K((X | U) : (Y | V)) is an interesting topic.

Conclusion

In the equation 1, K-dependence coefficient is fully defined with the entropy and conditional entropy. Because entropy and conditional entropy are fully defined with their joint distribution, the K-dependence coefficient is essentially defined by the same joint distribution. Also, K-dependence coefficient is able to measure the random variables’ situations of full dependence which is K( X :Y ) = 1, and full independence which is K( X :Y ) = 0. Those facts indicate that K-dependence coefficient fully utilizes the mutual information (or mutual relations) and multivariate interactions associated with the multiple random variables. Therefore, in terms of information associated with multiple variables (i.e. the multivariate joint distribution), K-dependence coefficient can be thought as “the best” player to measure a group of random variables’ dependence upon another group of random variables.

Same as the entropy, K-dependence coefficient only works for categorical random variables. I.e. K-dependence coefficient only works with categorical information, but not for interval or ordinal information. Although entropy can be defined for continuous numerical variables, unlike categorical variables’ entropy with a bottom line which is zero, the continuous numerical variables’ entropy has no bottom line, i.e. categorical variables entropy is an absolute measure while continuous numerical variables’ entropy is a relative measure. Currently, K-dependence coefficient is an absolute measure. For the example of relative measure, please see Kullback-Leibler divergence which measures continuous numerical variables’ distributions divergence.

Also, the readers are encouraged to explore K-dependence coefficient with the multivariate information, i.e. interactions associated with multiple variables. The probabilistic structure associated with multiple variables is much richer or more meaningful than mutual relations. The K-dependence coefficient with multivariate information offers a useful way to look into the probabilistic structure associated with multiple variables in more detail.

Acknowledgments

Author would like to express his sincere thanks to Professor Charles Lewis for his valuable suggestions and comments. His encouragement and support enabled the author to finish this paper.

References

1. Agresti A. Categorical data analysis.2002.

   [Crossref] [Google Scholar]

2. van Den Burg W, Lewis C. Some properties of two measures of multivariate association. Psychometrika. 1988;53:109-122.

   [Crossref] [Google Scholar]

3. Goodman LA, Kruskal WH. Measures of association for cross classifications. J Am Stat Assoc.1954;49(268): 732-764

   [Crossref]

4. Haberman SJ. Analysis of dispersion of multinomial responses. J Am Stat Assoc. 1982;77(379):568-580.

   [Crossref] [Google Scholar]

5. Kong LN, Lewis C. Multivariate information and interaction. J Stat Meet. 2009.
6. Theil H. On the estimation of relationships involving qualitative variables. Am J Soc. 1970;76(1):103-154.

   [Crossref] [Google Scholar]