Journal of Fertilization: In Vitro - IVF-Worldwide, Reproductive Medicine, Genetics & Stem Cell Biol
Open Access
ISSN: 2375-4508
ISSN: 2375-4508
Research Article - (2014) Volume 2, Issue 2
Background: IVF is divided into four stages: superovulation, egg-retrieval, fertilization and embryo transfer. The superovulation stage has specific protocols which include daily injections of hormones, decided by regular monitoring and testing involving cost intensive methods like ultrasound, to enable multiple ovulations per menstrual cycle. However, there is a lack of systematic planning and hormonal dosage prediction for successful superovulation using apriori information.
Methods: This work aims at developing a systematic outcome projection method for superovulation based on initial observations in an IVF cycle. The information about the size range and number of follicles was transformed to moment based information using the mathematical approach from crystallization literature. The follicle growth was modeled as a function of injected hormones and the properties of the follicles were represented in terms of moments. The model parameters were estimated using the data obtained from initial two days of observation. This information was used to project the follicle size distribution for the remaining cycle days.
Results and Conclusion: The model assumptions and its correlation to batch crystallization prove promising on comparison of the simulated follicle size and number to the observed data for the patients. The model prediction accuracy is determined by the statistical analysis of clinical data available for 50 superovulation cycles. Thus, it can act as an indicator for the success or failure of the ongoing superovulation stage in the IVF cycle and the decision whether to continue with the procedure or abandon it and start from donor eggs can be made, thus saving treatment cost and time on unsuccessful attempts.
Keywords: Predictive model, Infertility, Moment, Follicle
Infertility is the inability of a couple to achieve conception or to bring a pregnancy to term after a year or more of regular, unprotected intercourse. The World Health Organization (WHO) has estimated that about 8-10% couples experience some form of infertility problems. The occurrence of infertility in male and female population is almost identical. In most countries cost is a major hurdle in the access of infertility services. Most centers offering treatment for infertility operate outside the government financed health facilities. The treatment is only accessible to elites who can afford to pay for such high tech therapies. Even in a country like United States, the cost for an IVF cycle amounts to almost 20% the total annual income of a median American family. In developing nations, this cost is about 50% of the total annual income [1,2].
In-vitro fertilization is a process by which oocytes or egg cells are fertilized by a sperm outside the body in a laboratory simulating the similar conditions in the body and then the fertilized eggs or embryos are implanted back in the uterus for full term pregnancy. Superovulation [3] is the first stage of IVF in which multiple eggs are retrieved using drug induced stimulation of the ovaries. Major risks involved in IVF treatment are failure to conceive, multiple pregnancies, ectopic pregnancy, ovarian hyper stimulation syndrome. IVF is an expensive treatment. There are a lot of complications associated with each stage and hence the success rate is highly unpredictable. Also, the treatment strategies used are not modified according to the patient history. The success of IVF is primarily dependent on the quality and quantity of eggs or oocytes retrieved from the superovulation stage. Thus, superovulation is an important stage in the overall success of IVF.
It is important to understand the actual functioning of the ovaries in order to better understand the process of superovulation. The ovaries release periodic gametes (eggs/oocytes), produce steroid hormones; estrogen and progesterone. The process of follicle maturation, ovulation, corpus luteum formation and regression occurs repeatedly and its cyclic nature is measured in weeks. Usually only one egg ovulates per menstrual cycle. This selection of the follicle which enters into the ovulatory stage is affected by several factors, discussed by Baird [4]. The rise in Follicle Stimulating Hormone (FSH) level beyond a certain limit activates a single small follicle (2-4 mm diameter); this follicle dominates over all the other follicles for growth and ultimately enters the ovulatory phase. Multiple ovulations can be achieved by extending the period during which the level of FSH remains above the threshold. This is known as widening the gate for multiple ovulations. Thus, regulation of FSH secretion plays the most important role in determining ovulation and growth of the follicles. In our work, the model uses FSH dose in determining the kinetics for follicle growth. The other hormones like Gonadotropin Releasing Hormone (GnRH), Luteinizing Hormone (LH), estrogen, progesterone and human chorionic gonadotropin (hCG) also affect the phenomena, but their effect is negligible in comparison to FSH levels [5].
Superovulation has specific protocols [5] to be followed and includes daily injections of multiple agents from time durations varying in weeks to months. The protocols were developed to prevent premature ovulation and control the hormonal levels. The ‘long protocol’ is the most widely used and it involves injection of GnRH agonist that suppresses the endogenous functions of the ovary and the release of FSH and LH [5-7]. GnRH agonists are injected daily from the mid-luteal phase (usually the 21st day in a 28 day cycle) of the previous menstrual cycle, until follicle maturation is triggered. The exogenous FSH is injected from the 1st day of the next cycle and is continued for about 9 to 12 days depending upon the follicle growth until the maturation is triggered on the final day using the hCG.
The expense of IVF increases due to high cost of medication and frequent monitoring. The idea is to project the treatment response of the patient for the complete superovulation cycle by using initial two day response which shall act as an indicator for the success or failure of the cycle. In superovulation the multiple follicles with different sizes result into a Follicle Size Distribution (FSD). Since distributions are more common in processes where the system properties can be estimated by analyzing the representative distribution, we try to correlate mathematical modeling of the superovulation process to one of the most extensively studied particulate process of crystallization [8]. Preliminary results of this model appeared recently in Yenkie et al. [9].
Batch crystallization
Batch crystallization [8,10,11] is an industrial separation and purification process. The process objective is to enhance the product quality defined in terms of its shape and size by maintaining certain operating conditions. Maintenance of supersaturation condition is an essential aspect in crystallization. Supersaturation is a condition in which the solute concentration in the solution is higher than the solubility at a particular temperature. Thus, controlling the process temperature can maintain the desired supersaturation levels and hence enable the crystallization.
The crystalline particles are observed as a size distribution and the product purity is decided in terms of the size range of the crystals. Thus, the particle size is modelled as population balance. The general form of the population balance [10] can be written as Eq. (1).
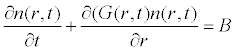 (1)
(1)
where, n is the number density distribution, t is time, r represents characteristic dimension for size measurements, G is the crystal growth rate, B is the nucleation rate.
Both growth and nucleation processes describe crystallization kinetics and their expression may vary depending upon the system under consideration. This complex equation involving partial derivatives can be simplified into a set of ordinary differential equations by using the method of moments [12]. The nth moment of the particle size distribution is defined as in Eq. (2).
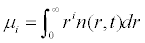 (2)
(2)
The crystals can be separated into two classes based on the kinetics [10,11] which cause their changes; (i) seed crystals - initially some crystals of the desired product are added to the solution. These crystals are known as ‘seed’ and they follow the growth kinetics, (ii) due to excessive supersaturation, new crystals are formed from the solution which is due to the nucleation kinetics. Thus, moments can be separated into seeded moments and nucleated moments. The generalized moment equations for the nucleated and seeded crystals as defined in literature by Hu et al., [10] are;
Moment equations for the nucleated crystals:
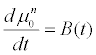
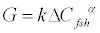 (3)
(3)
Moment equations for seeded crystals:
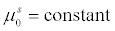
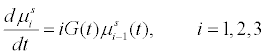 (4)
(4)
Thus, using the moment Eqs. (3) and (4), the complex Eq. (1) can be simplified and the mathematics of process modelling and control become easier.
Model development
In batch crystallization, the aim is to get maximum number and uniformity in crystal size and shape for all particles [11]. This correlates well with the objective of superovulation [6,7], ‘to obtain multiple eggs of similar size and quality’. To emphasize the point an analogy is presented in Table 1.
| Batch Crystallization | Superovulation (IVF stage I) |
|---|---|
| Production of multiple crystals | Production of multiple oocytes or eggs |
| Crystal quality is determined in terms of size distribution and purity | Oocyte quality is determined in terms of no abnormalities, similar size. |
| The rate of crystallization or crystal growth varies with time and process conditions | The rate of ovulation or oocyte growth varies with time and drug interactions |
| Process is affected by external variables like agitation, and process operating variables like temperature, pressure, etc. | Process is affected by externally administered drugs and body conditions of the patient undergoing the process |
Table 1: Analogy between batch crystallization and IVF superovulation stage.
The superovulation follicle growth model in general resembles greatly to the growth of seeded batch crystals. The aim of seeded batch crystallization is to allow the seeds added to the solution to grow to desired shape and size and truncate the process of nucleation by maintaining certain process conditions. The number of seeds added to the solution are constant and hence the zeroth moment of seeded batch crystals which corresponds to its number is constant [10]. Similarly, when we look at superovulation, the number of follicles activated during an IVF cycle is constant. Thus, the moment models for both the processes remain the same. The growth term which is a function of process variables like temperature and supersaturation in seeded batch crystallization will become a function of medicinal dosage in case of superovulation process.
The first four moments have a special significance [12] in terms of the properties related to shape and size of the particles. The zeroth moment is a representative of the number of particles, first moment of the shape, etc. The information provided by these moments will help in formulating a predictive model for superovulation. The desired outcomes for this stage can be specified mathematically in terms of the moment values.
Let us assume the activated number of follicles to be constant and hence the zeroth moment corresponding to it shall also have a constant value. The data from a successful superovulation cycle in Table 2 shows that during FSH dosage regime, as time progresses the size of the follicles increase.
| Size Bins(mm) /Time |
Number of Follicles | |||
|---|---|---|---|---|
| Day 1 | Day 5 | Day 7 | Day 9 | |
| 0 - 4 | 4 | 0 | 0 | 0 |
| 4 - 8 | 12 | 0 | 0 | 0 |
| 8 - 12 | 8 | 17 | 1 | 0 |
| 12 - 16 | 2 | 6 | 15 | 3 |
| 16 - 20 | 0 | 3 | 10 | 15 |
| 20 - 24 | 0 | 0 | 0 | 8 |
| FSH dose (IU/ml) | 150 | 75 | 75 | 75 |
IU – International units used for hormonal dosage measurement
Table 2: Variation of follicle size (diameter) with time and FSH dose in Patient A.
Moment evaluation
Conversion of the data available on follicle number and size to moments [12] using the Eq. (5).
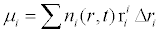 (5)
(5)
where μi - ith moment, ni(r,t) - number of follicles in bin of mean radius ‘r’ at time ‘t’, ri - mean radius of ith bin, Δr - range of radii variation in each bin. The moments evaluated are shown in Table 3.
| Sr. No | Time (day) | μ0 | μ1 | μ2 | μ3 | μ4 | μ5 | μ6 | FSH (IU/ml) |
| 1. | 1 | 52 | 188 | 820 | 4028 | 21556 | 123068 | 738100 | 150 |
| 2. | 5 | 52 | 308 | 1924 | 12740 | 89428 | 662228 | 5131684 | 75 |
| 3. | 7 | 52 | 400 | 3140 | 25120 | 204500 | 1691440 | 14189540 | 75 |
| 4. | 9 | 52 | 488 | 4660 | 45224 | 445492 | 4449128 | 44994100 | 75 |
Table 3: Experimental moments evaluated using Eq. (1).
Model equations
The rate expression for follicle growth is dependent on FSH administered. Thus, we can write the growth term as in Eq. (6)
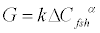 (6)
(6)
where G - growth term, ΔCfsh - amount of FSH injected, k, α - kinetic constants.
Assuming moment model, we consider only the first seven moments; zeroth moment corresponding to follicle number, the first moment corresponding to follicle size and the other 5 moments. The 1st to 6th order moments are being used since they help in recovering the size distributions more precisely as against lower number of moments [13]. It is essential to use 6 moments for recovering FSD since we have divided the data into six size bins depending upon the size of the follicles.
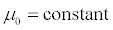 (7)
(7)
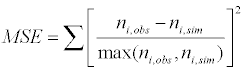 (8)
(8)
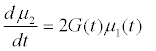 (9)
(9)
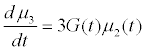 (10)
(10)
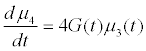 (11)
(11)
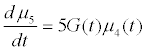 (12)
(12)
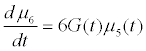 (13)
(13)
Solution method
We integrate the Eqs. (8) to (13) for predicting the kinetic constants in the follicle growth expression. Integrated equations for the moments are shown in Eqs. (14) to (19):
μ1 = Gμ0t + c1 (14)
μ2= G2μ0t2 + 2Gc1t + c2 (15)
μ3= G3μ0t3 + 3G2c1t2 +3Gc2t + c3 (16)
μ4= G4μ0t4 + 4G3c1t3+ 6G2c2t2 +4Gc3t + c4 (17)
μ5= G5μ0t5 + 5G4c1t4+ 10G3c2t3 + 10G2c3t2 +5Gc4t + c5 (18)
μ6 = G6μ0t6 + 6G5c1t5 + 15G4c2t4 + 20G3c3t3 +15G2c4t2 + 6 Gc5t + c6 (19)
Model validation
The current moment model will predict the moment values, however our desired output is in the form of follicle size distribution, thus in model validation the approach to obtain FSD from moment values is shown. The method is adapted from the literature by Flood [13], where he demonstrated a method to recover particle size distribution from moments in crystallization. In this method the particle size distribution is approximated using the inversion matrix, A shown in Table 4 along with a non-linear constrained optimization technique. Moment (μ)=A.n, thus we can write
| 2 | 6 | 10 | 14 | 18 | 22 | |
| 2 | 18 | 50 | 98 | 162 | 242 | |
| A= | 2 | 54 | 250 | 686 | 1458 | 2662 |
| 2 | 162 | 1250 | 4802 | 13122 | 29282 | |
| 2 | 486 | 6250 | 33614 | 118098 | 322102 | |
| 2 | 1458 | 31250 | 235298 | 1062882 | 3543122 |
Table 4: The inversion matrix A (6x6) to recover size distribution from moments.
n=A-1μ (20)
Using the model predicted moment values we evaluate n(r,t) using the ‘follicle number prediction algorithm’ and compare with the actual data to check the model accuracy. The number of follicles in a particular size bin on a cycle day of FSH dosage regime can be evaluated by using an algorithm based on constrained optimization [9,14]. The decision variables are the number of follicles in each bin per day in the cycle. Thus, by using this follicle number prediction algorithm, the moment model for follicle growth can be validated for a given patient.
Predictive value of the model
If the changes in the follicle size associated with the administration of hormones are monitored for two days, we can evaluate all the unknown parameters of the model. After evaluating them, the model can then be used to project the outcome according to the hormonal dosage on the successive days. The flowchart in Figure 1 shows the methodology for decision making regarding the continuation of the cycle or discontinuing it.
The follicle size measurements along with the FSH dosage for first two days will provide us with the 1st to 6th moment values for initial two days of observation. For projection of the FSD in the later days, we need the enlisted parameter values to be evaluated from the available data; k, α, μ0, c1, c2, c3, c4, c5, c6. Thus, we shall have 9 unknowns and 12 equations (two sets since we are using two day data). The 9 unknowns are evaluated using the Eqs. (14) to (19) for the first two days. From the parameter values and the moment model for the FSD the results are projected for the remaining cycle days. The projected results provide us with the idea about the success of the current cycle. If we observe desired number of follicles within a particular size range so as to retrieve them on the final day; the cycle can be continued with the projected FSH dosage, otherwise it is advisable to discontinue the ongoing cycle and start again. The patient and doctor can also decide to start directly with donor eggs.
Since we used the data for the initial two days observed, in this case the data for day 1 and day 5 has been used for patient A (see columns for day 1 and 5 in Table 2). Using this data the moments were evaluated from Eq. 5 (see row (1) and (2) of Table 3). Substituting the moment values along with the FSH doses in Eqs., (14) to (19), we had 12 equations to be solved for estimating 9 model parameters. These equations were solved in Matlab, and the parameter values obtained are listed in Table 5. It can be seen that the value of the evaluated zeroth moment from parameter estimation methods is quite close to the actual observations. Thus, the assumption of the zeroth moment being the representative of the number of follicles entering the growth stage proves reasonable as suggested by Baird [4].
| Parameter | Values |
|---|---|
| μ0 | 53.2 |
| k | 10 |
| α | -0.66 |
| c1 | 158.45 |
| c2 | 590.39 |
| c3 | 2186.86 |
| c4 | 21151.86 |
| c5 | 11104.30 |
| c6 | 100201.10 |
Table 5: Parameter values from the initial two day observation data:
Using the parameter values in Table 5, the results for the next days of the cycle were projected using the moment model. The moment values for the successive cycle days were evaluated by using Eqs. (14) to (19) and the parameter values estimated from the initial two day data. The FSD was back predicted using the correlation given by Flood [13] and the algorithm on follicle number prediction [9]. The results for FSDs predicted from the parameters estimated using the initial two day data as well as the complete data available for the patient A are also shown in Figure 2. The smooth curve shows the predicted values, while the discrete markers denote the actual follicle count. It is intuitive that the fit will be better for the all-day data (complete data) fit for a particular patient. It provides a check on the model accuracy as well as a good comparative estimate against the two day data projections. In this paper, all day data fitting and FSD predictions have always been used as an additional standard along with the clinical observations available from our collaborators for testing the claim, “two days of observation are sufficient to project the outcome of the superovulation cycle”.
Along with the results reported for Patient - A, 49 more such superovulation cycles was studied and their data for initial two days and on all days was used to project the superovulation outcome based on the same methodology. Table 6 summarizes the follicle number and size predictions from the clinical data available for 50 patients. The results from model projections for four more patients are reported in Figure 3-6. It can be observed that the predicted results are in well agreement with the actual observations.
| No. of Follicles observed (2 day) | No. of Follicles predicted (final day) | Mean size predicted (final day) | |||
|---|---|---|---|---|---|
| Number Range | No. of Patients | Number Range | No. of Patients | Size Range | No. of Patients |
| 4-10 | 36 | 4-10 | 34 | 6-7 | 7 |
| 11-15 | 5 | 11-15 | 6 | 7-8 | 5 |
| 16-20 | 3 | 16-20 | 4 | 8-9 | 17 |
| 21-25 | 4 | 21-25 | 4 | 9-10 | 17 |
| 26-30 | 2 | 26-30 | 2 | 10-11 | 4 |
Table 6: Follicle number and size predictions based on the available clinical data.
Statistical analysis
Statistical analysis was performed on the model predictions obtained for the fifty patients clinical data used in this study. The predictions of the ‘mean follicle size’ and the ‘Follicle Size Distribution (FSD)’ on the final day of FSH administration were compared with the actual observations. The percentage error was used as the measure of the accuracy of prediction for the mean follicle size on the final day of FSH administration and the sum of squares of error for the accuracy in FSD projection, which is referred as the ‘Mean Square Error (MSE) in model prediction’ in this paper. The error evaluations were performed by two methods (i) using the available data on all days and (ii) using the data for initial two days of observations. In MSE evaluation the follicles in the size bins corresponding to the desired size range of 9-12 mm were used.
In Figure 7, it can be observed that the mean follicle size prediction is better when all day data is used, which is a more likely result from the model predictions. In case of mean follicle size predictions using initial two day data, we observed more than 85% patients lie within the error range of 0% to 30%. Thus, even the two day data predicts the mean size for most of the patients with reasonable accuracy and hence regular monitoring and testing can be eliminated in most of the patients.
In Figure 8, the formula used for Mean Square Error (MSE) in model prediction is shown in Eq. (21).
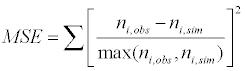 (21)
(21)
where ni,obs – number of follicles observed in the patient and ni,sim – number of follicles predicted by the model in the ith bin on last day of FSH administration.
Insight into parameter range
In addition to the measures of model accuracy we also checked the most probable parameter values and their range of variation to get more insight into the predictive value. We found out that for most patients the follicle growth term ‘G’ had values in the range of 0.3-0.6 and these cases the initial two day data was sufficient for FSD projection on successive days of the cycle. Also, for most patients the number of follicles entering the growth phase varied from 7–12 follicles, which means they had ‘μ0’ ranging from 14-24. These observations prove that if we have a patient whose parameter values for ‘G’ and ‘μ0’ from two day data model fitting are in the above mentioned ranges in those cases the model projections will provide better results and hence reduce the requirement for further testing.
Model prediction using additional data
As stated earlier, patients whose ‘G’ values are not in the range 0.3-0.6 show poor prediction with two day data. For these patients, we included three day data to see if the predictions improve. The Figure 9 shows the results using three day observation data for two patients F and G which had a MSE value greater than two. In Table 7 a summary of the results for patients F and G in terms of the comparison of mean follicle size and mean square error value for all day, two day and three day data predictions is shown. It can be seen that if we include an additional day data for these patients, the predictability of the model is enhanced.
| Patient | Measure of Accuracy | Data used | ||
|---|---|---|---|---|
| All day | 2 day | 3 day | ||
| F | Mean follicle size | 9.25 | 5.878 | 8.14 |
| Mean square error | 0.07652 | 2.644 | 0.417 | |
| G | Mean follicle size | 8.051 | 6.459 | 7.822 |
| Mean square error | 0.00899 | 2.432057 | 0.06473 | |
Table 7: Improvement in model predictions using three day data.
Previous work
Earlier work on follicular growth was mostly theoretical and involved the study of ovarian dynamics as a function of gonadotropins. Peters et al. [15] mentioned the emerging of a single follicle from a pool of small follicles. This selection phenomena was later mentioned by Baird [4] as the specific gonadotropin environment which facilitates the growth of dominant follicle while suppressing the others causing follicular atresia. The concept of ‘gate widening’ denoting the time for which the gonadotropin environment is favorable for follicle selection for maturation, enabled the selection of multiple follicles for ovulation. Chang et al. [16] also mentioned about the antral follicle count affecting the early follicle growth. Gougeon et al. [17] studied age-related changes to growing and non-growing follicles. Selgrade et al. [18] and Reinecke and Deuflhard [19], report about the hormonal control of the normal menstrual cycle in terms of mathematical equations. The model by Reinecke and Deuflhard [19] was highly complex involving the dynamic studies in the pituitary and ovaries. The single follicle dynamics was studied and the hormones LH and FSH were the ones affecting significantly. However, the model did not refer to external stimulation and multiple ovulations which is a novel aspect of the simplified moment model.
Study findings
The model tries to capture the actual number of follicles observed on the later days in the superovulation cycle by utilizing the initial observations as projection guideline. The results are not exact, but they provide a general idea about the successful growth of the follicles. It can help in deciding whether to continue with the cycle or discontinue it. It can save costs on futile superovulation cycles and help in deciding whether to start the IVF cycle from donor eggs. The method provides information about the number of follicles entering into the growth stage which provides an idea about the probable number of oocytes (matured follicles) to be retrieved. This will help in better decision making for the next stages in the IVF cycle.
From the statistical analysis of 50 patient cycles, we can conclude that in the cases where model error exceeds two, the initial two day observations are insufficient and hence in some cases more monitoring and testing will be required. The analysis of desirable parameter range and predictions using additional data provide the necessary distinction between cases where two the proposed method can work and when the patient may need additional observation and care.
Novelty of the work
In existing protocols the dosage prediction is done by trial and error and involves daily monitoring using cost intensive techniques like ultrasound. The work performed in this research is the first attempt to model follicular growth in the form of differential equations, which are able to predict the follicle size and number changes with time. It is also the first study where the customized model has been developed from the initial response of the patient in the same cycle to project the outcome on the successive days.
Overall benefit in terms of some key factors
Financial benefit: The customized model for each patient cycle and the outcome projections will ensure a better success rate thus saving the costs on unsuccessful attempts. It will reduce the requirement of pathological tests and expensive monitoring methods.
Time saving: If the initial two day observations can project the success or failure of the superovulation cycle, time can be saved on futile attempts. The decision to start the IVF cycle from donor eggs can be made within a few days of the start of the cycle.
Emotional factor: The emotional state of the patient is affected significantly since the treatment involves interference in the hormonal balance of the body. The model prediction can alleviate this problem.
Health risks: The superovulation failures can be very hazardous. Higher dose of medicines may result in ovarian hyperstimulation syndrome [3,20], which at times can be life-threatening. Also the external intake of hormones may increase the chances of ovarian cancer.
Limitations
Biological systems are inherently uncertain; in this work we have not considered the associated uncertainties [11,14]. In the current study, the decision of continuing or discontinuing the cycle can be made only after the cycle has been started. Therefore, when the model predicts an unsuccessful outcome the patients still have to undergo some initial days of treatment which are cost intensive and puts an emotional burden since they start the treatment with a lot of hope.
Summary
On the whole, the current work provides a novel methodology for predicting the probable outcome of the superovulation cycle and saving overall IVF treatment costs. The moment model developed for IVF superovulation on the lines of the well-known process of batch crystallization provides a new approach in modeling biomedical processes. The FSD predictions by the model are in good agreement with the actual size distributions. The advantage lies in the treatment variation depending upon each patient’s initial response. Thus, drug dosage can be customized and optimized. The proposed approach will help the medical practitioners to modify the treatment protocols and ensure a higher success rate with lesser chances of health risks.
The current model can be used to formulate a mathematical function relating to the follicle size, their growth and number. The aim of superovulation is to maximize the number of follicles retrieved in the desired size range. The mathematical model would prove beneficial in predicting the optimal dosage regime for desired outcome by application of optimal control (Diwekar [14]) theory to the system. The current model does not consider variability depending upon the patient’s medical history, age and treatment response. This model can be extended to involve such variability and solve the problem for optimal dose. Thus, the current model has several advantages in terms of predictive value and will aid the medical community and society in an area which was previously based on trial and error and required continuous medical supervision. Most importantly, it will aid in enhancing the IVF success rate.
We thank the Jijamata Hospital in Nanded, India for help with the data for superovulation. We also thank the Institutional Review Board at UIC for approving the current research to meet with the requirements of Protection of Human Subjects research under the Protocol # 2012-0317 titled ‘Understanding the Superovulation Stage of IVF Process for Optimal Drug Delivery’.