Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2015) Volume 5, Issue 6
Molecular dynamics simulations have been performed on the aqueous solutions of Poly(vinyl methyl ether) (PVME) at various concentrations. Both radial and spatial distribution functions are used to investigate the detailed hydration structures. The structures of water are found to get increasingly concentrated when polymers are introduced and the water motions are severely hindered by the polymer matrix. At low concentrations, larger populations of tt conformers in meso dyads than those at higher concentrations are found and this phenomenon is believed to be due to the increase of water molecule bonding to two ether oxygens in meso dyad. At higher concentrations the sizes and conformations of polymers are quite similar with those in bulk. A transition of hydrogen bond fractions between PVME and water at around the concentration of 0.3 is observed and this value coincides perfectly well with the results of conformational analysis and Raman spectra. Second neighbor hydrogen bond statistics showed that complicated hydrogen bond networks take the lead at low concentrations, but single hydrogen bonds as well as isolated clusters composed of 2-4 water molecules are found common around each polymer repeat unit.
<Keywords: Molecular dynamics; PVME; Hydration structure; Solvation
Aqueous solutions of poly(vinyl methyl ether) (PVME) exhibit lower critical solution temperature (LCST) miscibility behavior with moderate critical solution temperatures around 35 ~ 37? [1-3]. The polymer dissolves below this temperature but phase separates when heated. In common cases, the LCST behaviors of aqueous polymer solutions can experimentally be sorted into three types [2,4]: type I represents the classical Flory-Huggins (FH) phase behavior, whose liquid-liquid phase separation critical composition shifts towards lower polymer concentrations for longer polymers; while the critical composition of type II hardly changes even for polymers with infinite molar masses; the LCST curves of type III are bimodal and have two stable critical compositions, one at lower polymer concentration (type I) and the other at higher polymer concentration (type II). The phase behavior of the PVME/H2O system belongs to type III at physiological temperatures [2].
This bimodal feature of the atypical phase behavior should, from the atomistic point of view, originates from the special hydrophilic and hydrophobic interactions between water and PVME [3,5]. The hydrophilic sites (ether oxygens) stabilize the aqueous solution by forming hydrogen bonds (HB) with neighboring water molecules while the hydrophobic groups (particularly the methyl groups due to the polarization of ether oxygens) destabilize the solution by altering the normal hydrogen bond network structure of water close to the polymer chains. The resulting structures of water around the hydrophobic groups were referred to as the “icebergs” by Nemethy and Scheraga [6], and also by Frank and Evans [7]. These two interactions compete with each other with increasing temperature until phase transition occurs [3]. Wu et al. also utilized FTIR spectroscopy to investigate the microdynamics mechanism of the PVME aqueous solution, and they found the hydrogen bonds between hydrophilic groups and water and the hydration interactions between hydrophobic groups and water are completely reversible [5].
There has been extensive investigation [1,3-5,8-16] on the nonclassical phase behavior and the above mentioned two sorts of interactions in the PVME/H2O system. From changes in the nearinfrared and calorimetric parameters with the variation of concentration, Maeda [3,10] proposed that an average of 2.7 water molecules per chain repeat unit in PVME solutions formed stable molecular complex through hydrogen bonding to the ether oxygens and additional 2.3 water molecules formed “icebergs” around the methyl groups, over 5 water molecules were “free”, namely they had nearly no interaction with the polymer. Nies et al. [1,4,14] concluded that experimental data from small angle neutron scattering did not support the existence of a stable molecular complex as the mixtures were characterized by Ornstein- Zernike-like composition fluctuations even at the temperature as low as 10?. The bimodal LCST phase behavior of the PVME/H2O system was also predicted, by way of the Wertheim Lattice Thermodynamics Perturbation Theory (Wertheim-LTPT), together with two adjacent narrow upper critical solution temperatures (UCST) miscibility gaps at low temperature, and these results were in agreement with experimental observations. The predicted solid-liquid equilibrium of the solvent showed a pronounced drop in melting temperature at intermediate weight compositions of 40 ~ 70 wt %. This peculiar concentration dependence of the melting line of water provided a new explanation for the double melting endotherm observed in (MT)DSC rather than being linked to the melting of bound and free water, namely the formation of a stable intermolecular complex.
The phenomenological results from experiments and theoretical predictions could not provide detailed molecular insights into the observed anomalous phase behavior. Previous work in our group [12] utilized quantum mechanics (QM) calculations to investigate the interactions between the PVME model compound and clusters of 2 ~ 5 water molecules, and the detailed molecular packing structures with relatively lower energies were obtained. The most stable configurations obtained were those with single HBs for clusters with no more than 3 water molecules and those with double HBs for clusters with more than 3 water molecules. The HBs between water and the ether oxygens were proved to be stronger than those between waters, namely these HBs are shorter in length and lower in energy. The hydrophobic interactions, called “QHBs” (quasi-hydrogen bonds), were found to coexist and associate with the HBs in many of those configurations. Different hydration features and mechanisms were analyzed and an uneven distribution of water adsorption on the polymer was found to be preferred. An average of 1.5 water molecules per repeat unit was suggested if all units of the polymer were bound with water.
Despite that the detailed configurations of possible packing structures can be successfully derived, QM calculations are still unable to describe the influence of polymer chain connectivity and conformation on the hydration structures. With the fast development of computational capabilities, atomistic molecular dynamics (MD) simulations have been extensively used to investigate the aqueous solutions of organic compounds, such as alcohols [17], Urea [18], amides [19] and dimethylsulfoxide [20]. Tamai et al. [8] utilized the AMBER/OPLS force field [21] and SPC/E water model [22] to simulate the hydrogel model structures of PVA (poly vinyl alcohol), PVME and PNiPAM (poly N-isopropylacrylamide). It was found in the hydrophilic regions the average number of hydrogen bonds between water molecules was smaller by 1.0 ~ 1.9 than those in pure water, and the defects of water-water hydrogen bonds were completely compensated by the water-polymer HBs for PVA but not for PVME and PNiPAM; In the hydrophobic regions, the average number of HB between water molecules was only slightly smaller than those in pure water, the water-water HBs were stabilized in the hydrophobic regions especially for PVME and PNiPAM, and this was deemed to be owing to the hydrophobic hydration effects. It was also found that in the regions out of the first hydration shell, the HB numbers were not at all influenced by the polymer matrix. In their simulations, the stability of HBs was much more enhanced in the systems with lower water contents than those with more water, and this phenomenon was attributed to the constraints on the mutual orientation of water and polar groups imposed by the hydrophobic side group at large polymer concentrations. While in their simulations, the concentration dependence of the hydration structures of PVME was not fully described.
In the present work, MD simulations have been performed on the aqueous solutions of PVME at concentrations varying from 0 to 100 wt %. The OPLS-AA force field [23,24] and the TIP4P water model [25] are used, for TIP4P is the only one with a realistic dimmer structure and its quadrupole is the most realistic among the most frequently used water models [26-28]. In addition, the most recent OPLS-AA force field parameters have been optimized with the TIP4P water model for better description of the interactions between water and organic substances [27].
Molecular models and force field
Classical molecular dynamics simulations of aqueous solutions of PVME were carried out using the GROMACS simulation package [29] with the OPLS-AA force field and the TIP4P water model. The potential functions adopt the form in which the former two terms represent the harmonic vibrations of bond lengths and bond angles, respectively; The third term stands for the dihedral potentials, whose OPLS parameters are translated into the Ryckaert-Bellemans [30] type in GROMACS; The latter two are non-bonded interactions including the Lennard-Jones (L-J 12-6) and the electrostatic interactions. Table 1 lists the diagonal non-bonded parameters for PVME and the TIP4P water, in which ε and σ are the well depth and collision diameter for the L-J 12-6 interaction, q is the polar charge, and m is the atomic mass. The standard combination rules [24] are used for the off diagonal non-bonded atomic pairs
| Atom | ε (kJ/mol) | σ (nm) | q |
|---|---|---|---|
| PVMEa | |||
| C1 | 0.276 | 0.350 | -0.12 (-0.18b) |
| C2 | 0.276 | 0.350 | 0.17 (0.14b) |
| C3 | 0.276 | 0.350 | 0.11 |
| Op | 0.586 | 0.290 | -0.4 |
| H | 0.126 | 0.250 | 0.06 (0.03c) |
| TIP4P | |||
| Ow | 0.649 | 0.315 | 0.00 |
| Hw | 0.000 | 0.000 | 0.52 |
| Mwd | 0.000 | 0.000 | -1.04 |
aC1 and C2 are backbone carbons and C2 connects with the side group; bChargesfor carbons at chain ends; cCharge for hydrogens bonded to the carbon next to Op;dThe dummy atom in the TIP4P water model.
Table 1: Non-bonded Potential Parameters for PVME and the TIP4P water model.
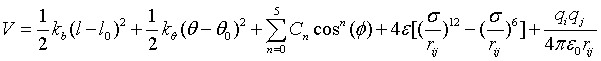 (1)
(1)
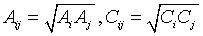 (2)
(2)
where 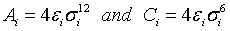 . Intra-molecular interactions between all pairs of atoms separated by more than three bonds are regarded as ordinary non-bonded interactions, while the 1-4 interactions are monitored by both the dihedral potentials and the ordinary non-bonded interactions scaled by 0.5 [24].
. Intra-molecular interactions between all pairs of atoms separated by more than three bonds are regarded as ordinary non-bonded interactions, while the 1-4 interactions are monitored by both the dihedral potentials and the ordinary non-bonded interactions scaled by 0.5 [24].
Simulation details
All PVME chains used in the current study contain 44 backbone carbons and all repeat units are connected head to tail. The chains are atactic and were generated according to the Monte Carlo method described in the appendix with steric ratio meso:racemic (m:r)=1:1. Table 2 lists the number of PVME chains np, number of water molecules nw, the number of water molecules each polymer repeat unit can ideally be assigned nw/nmon and the weight concentration cp of each system. The initial amorphous structures were built using the Amorphous Builder in Accelrys Materials Studio 3.1, 20 structures were built for each system and the ones with the lowest potential energies were chosen for subsequent procedures. These chosen structures were then “solvated” in water using the “genbox” command in GROMACS and each system underwent hundreds of steps of energy minimization with the conjugate gradient (CG) method.
| np | nw | nw/nmon | cp (wt ) |
|---|---|---|---|
| 0 | 2218 | / | 0 |
| 1 | 2060 | 93.6 | 0.03 |
| 4 | 1939 | 22.0 | 0.13 |
| 8 | 1585 | 9.0 | 0.26 |
| 12 | 1385 | 5.2 | 0.38 |
| 16 | 987 | 2.8 | 0.54 |
| 24 | 588 | 1.1 | 0.74 |
| 30 | 341 | 0.5 | 0.86 |
| 40 | 0 | 0 | 1.00 |
Table 2: Simulated samples.
The constant particle, constant pressure and constant temperature (NPT) MD runs were then carried out for 4-10 ns depending on the concentrations of the solution systems, and the equilibrium was monitored by the potential energies, densities, hydrogen bond numbers and polymer conformations. The canonical ensemble (NVT) sampling MD simulations followed and extended for another 20 ns. The temperatures of all solution systems were maintained at 300 K with the Nose-Hoover [31,32] temperature coupling method, and the pressures were isotropically coupled to 1 bar with the Parrinello- Rahman [33] pressure coupling method. The bulk PVME system was firstly equilibrated at 600 K then annealed to 300 K and another 10 ns further equilibration was performed before NVT runs. A cutoff of 1.2 nm was used for the Van der Waals interactions. The Particle Mesh Ewald (PME) method [34,35] was used for long range electrostatic corrections and the long range dispersion corrections were also implemented for both energy and pressure. All bonds in polymers were constraint with the Lincs method [36] and the rigid structure of water molecules were maintained with the Settle method [37] during all MD simulations. A time step of 1 fs was used and the trajectories were recorded every 1 ps.
Radial and spatial distribution functions
The structure of liquid can often be well characterized by the radial distribution function (RDF) of atomic density,
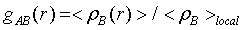 (3)
(3)
which represents the probability of finding particle B within the range r+dr around particle A. The spatial distribution function (SDF) takes into account both radial and angular correlations between particles, and allows three dimensional (3D) visualization of the local atomic densities, thus it provides much more detailed information on the local structural environment than RDF does. The visualization of SDF is often described by iso-surfaces, which show the distribution of particles with densities several times that of average around a reference atomic group. To calculate SDF, a local coordinate system has to be defined with a reference structure. For water, the local coordinate is defined so that oxygen stays at the origin and the whole molecule lies in the XY plane. For PVME repeat unit, the ether oxygen is set as the origin and the plane formed by the oxygen and the two connected carbons is regarded as the reference, so that the backbone configurations and conformations do not influence this local coordinate system.
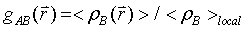 (4)
(4)
Definitions for HB and QHB
The formation of a hydrogen bond needs an electronegative proton donor (D) and an acceptor (A) with at least one lone pairs of electrons. The atomic pairs in our simulations are considered to be hydrogen bonded if the distance between D and A is within 0.35 nm, and simultaneously the angle between the DA axis and one of the DH bonds is smaller than 30°. This geometrical criteria is the same as that used by Luzar and Chandler [38,39]. For QHBs, there exist various definitions in literatures and our definition refers to that of Li et al. [19]. Based on the Van der Waals diameter [40] and quantum mechanics calculations [12], the QHBs are defined with the distance r(C-O)<0.372 nm and the angle C-H…O>150°.
Diffusion coefficient of water
The diffusion of water can be estimated from the Mean Square Displacement (MSD) within a time period of t
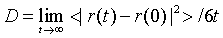 (5)
(5)
The experimental [41] diffusion coefficient of pure water is (2.11- 2.66) × 10-5 cm2/s at 298 K. The calculated value at 300 K is 3.78 × 10-5 cm2/s, which is slightly larger than the experimental result but still corresponds well with the simulation values (3.73 × 10-5 cm2/s at 298 K) using the same water model.
Measurements of the PVME Raman spectra
Poly (vinyl methyl ether) with Mw=60.5 kg/mol and Mw/Mn=3 was synthesized in the group of Prof. Nies in Universiteit of Leuven. Aqueous solutions with concentrations cp=0.1, 0.3, 0.6 and 0.8 as well as the bulk were prepared for use. The Raman spectra were recorded at room temperature using a JY-HR800 (Jobin Yvon) Raman micro spectrometer. A Nd:YAG laser (532 nm and 6 mW) was used as the excitation source. The Isotropic Raman scattering intensities were calculated from the parallel and perpendicular components of the experimentally measured Raman scattered light: 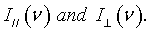
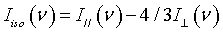 (5)
(5)
The 314 cm-1 band of carbon tetrachloride was used to verify the accuracy of the scattering geometry and light collection optics used, and gave the expected value of 0.75 within 2%.
Densities and excess volumes of mixing
From NPT runs, the obtained equilibrium density of pure water (0.993 ± 0.006 g/cm3) corresponds well with experiments (~ 0.997 g/ cm3). While the density of bulk PVME at 300 K is 1.019 ± 0.004 g/cm3, slightly smaller than the experimental value of 1.061 g/cm3 [42]. This is probably caused by the relatively shorter chains simulated than used in experiments [43].
The binary mixtures exhibit strong non-ideal behavior as reflected by the excess specific volumes in Figure 1. The values are calculated from the equilibrium densities of each solution system and those of pure water and bulk PVME. All excess specific volumes are negative and their standard deviations are smaller than the symbols shown in the Figure. The largest excess specific volume is anticipated to be reached at cp=0.5 ~ 0.7, which corresponds well with the experimental values inferred by the Redlich-Kister [44] polynomial [13].
Comparing with the experimental data in Figure 1, all calculated excess specific volumes are smaller due to the conformations of the relatively short chains simulated. In aqueous polymer solutions, not only hard core volume packing and free volume effects are operational but also volume effects related to the directionality of the hydrogen bonds between water molecules and those between water molecules and PVME repeat units must be considered [13]. The conformations of the shorter chains simulated should in principle have led to the smaller excess volumes of mixing. Despite these differences, the simulated systems have in general well captured the essential features of PVME aqueous solutions.
Structure and diffusion of water in solutions
Local water structure variation with concentration: The results of RDF for atomic pairs Ow-Ow at all concentrations investigated are shown in Figure 2. All RDFs have prominent first peaks at around 0.276 nm, and nearly no position changes are observed. The RDF of Ow-Ow for pure water (not plotted for clarity) is nearly identical with that for cp=0.03. All curves show clear peaks of HB, second neighbor HB and even third peaks of longer correlations, longer correlations are diminished because of the diffusion of water molecules. The near neighbor correlations show almost similar behavior for systems below cp=0.6, while in the water-poor mixtures namely cp=0.74 and 0.86 the g(r) curves show sliding down beyond the second minimum. Together with the enhanced first and second peaks, these phenomena are deemed as the results from the association of water molecules as dimers or clusters [45,46], and such effects get stronger with the increase of concentration in these systems.
The SDFs in Figure 3 have provided more detailed and clearer pictures of the local water HB structures. The first neighbor HBs are characterized by the three density caps: two caps over the H atoms are due to proton accepting neighbors, and the single large density cap over the O atoms is due to proton donating neighbors. The density caps are plotted with the same iso-surface thresholds and the enhanced waterwater correlations with concentration are clearly observed when more polymer chains are introduced. It is obviously shown in the figure that the low concentration one has relatively thinner density caps and the high concentration one has thicker density caps. This indicates that in the high concentration, with small amount of water molecules, most are confined within the first neighbor shell of polymers, taking nearly all interaction configurations even with higher energies. And in the low concentration, large amount of water molecules has huge interaction configurations to be selected according to lower energies, avoiding the small population configurations in the first neighbor shell.
Water diffusion in solutions: The mean square displacement of water molecules are plotted in Figure 4 for all systems including pure water. At low concentrations, these water molecules show diffusion behavior, for their MSDs show linear relation with time. The diffusion coefficient characterized by the slope of these curves show monotonic decrease as the polymer concentration is increased. At high concentrations, the MSD curves even approach plateau values at longer time period, which shows that the presence of polymer matrix significantly decreases the mobility of water molecules. The cages and HBs in polymers, discussed in the previous section, might have trapped the motion of these water molecules.
The solvation structures of the Op and CH3 groups: For the investigation on the solvation structures of PVME repeat unit, the RDFs of atomic pairs Op-Ow and C3-Ow at various concentrations are plotted in Figure 5. With the increase of concentration, HBs between PVME and water also get concentrated after a concentration of 0.38. Only slight migration of the first peak is observed to increase from 0.269 nm to 0.273 nm (given in Figure 6), which are smaller than those of Ow-Ow (see Figure 2) which corresponds well with our previous quantum calculations [12]. At high concentrations, the HB having a relatively longer bond length is manifested by SDF for concentration 0.86 (Figure 3) under confinement, taking the high energy configurations. While at low concentrations with abundant water molecules, the association between hydrophilic and hydrophobic interactions was found to shorten the HBs [12]. But a small part of the ether oxygens have chances to form double hydrogen bonds, which makes the HBs longer, later statistical results of HB will demonstrate that such double HBs are scarcely seen at all concentrations.
In addition, the first minima shift toward longer distances and the first peaks get broader at high concentrations, suggesting that there are changes of HB structures. The second peaks are much broader than the first ones and at low concentrations, the heights of second peaks of Op-Ow RDFs are even larger than those of the first peaks, which might indicate that water molecules from the second hydration shell form hydrogen bonds to the water molecules already donating their protons to the ether oxygens. But this is not necessarily the case, specific structures around adjacent atoms may also cause such welldefined peaks. Compared with the slight increase of peak positions of the Op-Ow RDFs, The peaks of the C3-Ow RDFs decrease more significantly from 0.367 nm to 0.355 nm. These QHBs are much weaker than HBs, and the hydration effects will have much influence on their structures.
For a clearer view of how water molecules are arranged around the PVME repeat units, SDF corresponding to the atomic pairs referred to above are plotted in Figure 7. Only the SDF at the concentration of 0.54 is shown, for clear distinctions are not found at different concentrations since the peak height differences of g(r) at other concentrations are much smaller than those of water as seen from comparisons between Figures 2 and 5. With the polymer repeat unit as reference (C1 is plotted just for reference), the density map of water around the repeat unit is shown. The iso-surface covering the reference ether oxygen represents the strong HBs between water molecules and the ether oxygens, such iso-surface corresponds to the first peak in Figure 5a. As for the second peaks in the Op-Ow RDFs, there exit two sorts of interactions: the second neighbor HBs and the QHBs around the methyl group. It is also evident from Figure 7 that the second neighbor HB iso-surface mixes with the QHBs, suggesting the cooperative association between HB and QHB, which results in complex water clusters around PVME. This result corresponds well with our previous quantum caculations [12].
Polymer backbone conformations: The polymers in aqueous solutions often have significant conformational changes due to the specific hydrophilic and hydrophobic hydrations. As an overall estimate of the polymer conformations, the radii of gyrations of PVME in solutions are shown in Figure 8. At low concentrations, the polymers adopt relatively extended conformations due to the specific hydrophilic and hydrophobic hydrations. With the increase of concentration, polymers aggregate and interpenetrate each other, and their sizes approach those in bulk.
We now have a look at the experimental Raman spectra at various concentrations in Figure 9. The peaks with most significant variations are denoted as a, b, c, d. Similar shapes of the peaks are observed for concentrations above 30 wt %, but for the spectra at low concentrations drastic differences are observed, the peaks of c and d level off and form plateaus. According to our previous experience [12,47,48], the peaks of a and b are related to the stretching modes of C-C and C-O; while c and d are mainly caused by the bending modes. The bending modes of C-C-C are directly related to the backbone conformations and the spectra around 400~500 cm-1 have been regarded as the disordered longitudinal acoustic mode (D-LAM) regions which well represent the variations of the long sequence of PVME conformations [47,48]. As far as the radius of gyration is concerned, the Raman spectra are in good correspondence with our MD simulations.
In order to discover the detailed conformations of PVME in solutions, Figure 10 shows the fractions of the major isomeric dihedral pairs found for both meso and racemic dyads along the chains obtained in the simulation, and the ones with very small populations are not shown for clarity. For the meso dyads, the gt conformers are preferred and the drastic drop of tt conformers around the concentration of 0.3 are the most apparent. In the bulk state, the tt conformers in meso dyads are not at all preferred, which takes only ~5% in the conformer pairs in meso dyad. But in the hydration, the significant change of the tt conformer around 0.3 demonstrates that the hydration of PVME helps formation of the tt conformer through HB interaction of at least a water molecule bonding to two ether oxygens in meso dyad as shown in Figure 11. Compared with the meso dyads, the tt conformers are preferred in the racemic dyads, and the tt conformer pair show some increase when the concentration increase above 0.3. In general, the polymer conformations are similar with that in bulk for solutions of high concentrations; but the conformations of dihedral pairs at low concentrations have more significant variations than those at high concentrations, and the conformations change at a critical concentration of 0.3. The variation of this conformer change around the polymer concentration of 0.3 shows similar behavior of the Raman spectra, in which the emergence of peaks also occurs around this concentration.
During the hydration of PVME, it has changes 1) in the radius of gyration, 2) in the conformational distribution for the tt conformers, and 3) in the Raman spectral profiles of D-LAM. Obviously, the three changes are correlated. The global size increase is due to the local conformational variation, which is predominated by the tt conformation. Geometrically, it is reasonable, because among the end-to-end distances (within four backbone bonds) of various conformation dyads, the tt conformation dyad has the longest end-to-end distance. It leads to local structure expansion and the global size increase eventually. D-LAM shows the conformational structure transition occurs accordingly.
HB and QHB statistics: For aqueous solutions of small compounds, water should be meanly distributed around the solute and the structure of the solute should not have much difference, but for polymers, the local chain conformation changes upon solvation. For PVME, each repeat unit is only possible to form at most two hydrogen bonds with water, and the hydrogen bonding in polymers should not be uniform along the chains. In order to get more quantitative picture of the solvation structures of PVME solutions, We have counted the factions of units forming i (i=0,1,2) HBs or QHBs according to the geometrical definitions defined in section 2.4.
Figure 12a gives the fractions of Op with i (i=0,1,2) HBs with water. At low concentrations, most of the ether oxygens (over 90%) are able to form HB with water, but even at the lowest concentration investigated, there still exist ~10% ether oxygens which are not able to form efficient HBs with water due to the close contacts between local chain segments caused by the flexibility of the polymer chains. With the increase of concentration, the fraction of such HBs decrease drastically, which is, in our opinion, due greatly to the conformational change as mentioned in the previous section. The conformational changes will cause significant variations of the solvation structures as HBs or the association between HBs and QHBs. The transition at around 0.3 matches perfectly well with the results of conformational analysis and Raman spectra as previously discussed. The further decrease of HB fractions at higher concentration is conceptually attributed to the deficient number of water surrounding the polymer chains. Due to the existence of negative cooperativity effect [49] for HBs, the fractions of repeat units with double HBs are very small, but still possess a transition around the concentration of 0.3. And moreover, recent work of Nies [4] measured the demixing enthalpy of the aqueous solutions of a mono-dispersed low molecular weight (about 140 backbone carbones) PVME utilizing modulated temperature differential scanning calorimetry (MTDSC), and found there also exist a transition around the concentration of 0.3. But their results level off at low concentrations and decrease linearly over 0.3.
Figure 12b and c depicts the fractions of Ow with i (i=0,1,2) HBs with PVME and water respectively. With the increase of concentration, the fractions of HBs with PVME increase and at high concentrations significant amount of water have been observed to be hydrogen bonded to two polymer repeat units, which might be adjacent or from two different chains. Here, the numbers of double HBs have higher fractions at high concentrations. Water can serve both as acceptors and donors, but in Figure 12c we just count those serve as donors or acceptors and thus the water molecules can also just form at most two HBs with water, so that they can be directly compared with those HBs between polymer and water. With the increase of concentration, the fractions of water molecules that form only one HB with other water molecules increase while the fractions of those forming two HBs decrease, which indicates the severe interruption of normal water HB networks and the tendency to form isolated water clusters.
Figure 12d describes the fractions of the CH3 group with i (i=0,1,2) QHBs with water, the fractions of QHBs are quite minor compared with those of HBs. The increased fraction of QHBs at low concentrations is strong evidence that the associations between HBs and QHBs have lead to the increase of tt conformers in the meso dyads.
Cluster analysis: The possible cluster structures with 1-5 water molecules around PVME repeat units have been surveyed with QM in our previous investigations [12]. In this study we have taken into account the polymer chain connectivity and the dynamic features of real systems, the hydration structures might not well be completely the same with the cluster structures obtained in vacuum. Based on the statistical results in Figure 12, we could make assumptions that all water molecules are within the clusters around the polymer, then at the concentration of 0.86 each repeat unit that has HB bonding with water can be assigned 1.56 water molecules, namely the clusters have on average 1.56 water molecules, this number is consistent with predictions (1.5) in our previous study [12]. With the same assumption, the clusters will have 2.77 and 5.18 water molecules at concentrations of 0.74 and 0.54 respectively. But it is apparent that not all water molecules in these solutions are in the clusters.
Through the RDFs and SDFs in previous sections, we have observed that around the polymer repeat units water molecules form at most two hydration shells. A representative snapshot of the HB bonded PVME-water cluster is shown in Figure 13a. Most ether oxygen form first shell HB with just one water molecule, namely very few form hydrogen bond with two water molecules as is the case for the negative cooperativity effect [49]. As far as the second neighbor HB is concerned, some PVME repeat units form clusters with 2, 3 and 4 water molecules as noted by the circles, the oval-shaped circle designates the chain effect in HB between water molecules. The clusters inter-correlate with each other, forming relatively stable configurations.
Figure 13: a) a representative snapshot of the HB bonded PVME-water cluster, the dotted lines represent the HBs; b) Concentration dependence of the fractions of PVME repeat units with i (i=0-5) water molecules in their surrounding clusters. The data for the squares are the same with those in Figure 12 a). The lines serve to guide the eye.
We have also counted the fractions of repeat units with i (i=0-5) water molecules which are hydrogen bonded to the first shell water molecules already donating their protons to the ether oxygen. These results are added to those shown in Figure 12a, and the resulting cluster size estimations are plotted against concentration in Figure 13b. Here, only clusters with no more than 5 water molecules are shown, because the fractions of clusters with more water molecules are negligibly small. At low concentrations, clusters with 4 water molecules take the lead, in such structures all hydrogens and lone pairs of the first shell water molecules are hydrogen bonded and the entire structures form complicated 3D HB networks. The number of such structures decreases as the concentration increase due to the change of polymer conformations as demonstrated in section 3.4, and they do not take overwhelming proportions at high concentrations. The fractions of clusters with 5 water molecules are barely perceivable at low concentrations and look very much similar with those of double HBs in Figure 12 a, since only double HBs can form more than 3 second neighbor HBs. With increase of concentration, fractions of 3 water clusters show slight decrease while those of 2 water clusters obtained slight increase, at high concentrations the regional clusters composed of 2-4 water molecules are commonly seen, but in these systems most of the repeat units are wrapped in polymers due to interchain packing. What is worth mentioning that isolated HBs between water and ether oxygen are seen to take ~ 3% at the concentration of 0.86.
Through atomistic molecular dynamics simulations of the PVME solutions with various concentrations at 300K, structure variations of water, polymer and their correlations were analyzed. The water structures get increasingly concentrated when polymers are introduced, and the water motions were severely hindered by the polymer matrix. The Op-Ow RDFs show two well defined peaks, the first peaks represent the HBs between the polymer and water and they have shorter lengths than those between water molecules; the second peaks are much broader and are found to be contributed from both the second neighbor HBs and the QHBs around the CH3 groups.
At low concentrations, the polymers adopt relatively extended conformations and the tt conformers in meso dyads undergo drastic decrease at the concentration of around 0.3, which is believed to be due to the increase of water molecule bonding to two ether oxygens in meso dyad at low concentrations; while other conformers have less apparent variations. At higher concentrations the sizes and conformations are quite similar with those in bulk. And the structural variations of polymers are in qualitative agreement with the observations from the Raman spectra.
Solvation mechanisms different from small molecules were proposed for PVME solutions through the counting of HBs and QHBs. The transition of fractions of Op with HBs with water at around 0.3 coincides perfectly well with the results of conformational analysis and Raman spectra, which indicates the hydration structures are greatly influenced by the conformational changes in polymer. Fractions of water molecules hydrogen bonded to PVME increase with concentration and at high concentrations significant amount of water have been observed to be hydrogen bonded to two polymer repeat units which might be within the same chain or from two different chains.
The fractions of clusters around PVME repeat units with i (i=0-5) water molecules are well designated and it is found that the 3D HB networks take the majority in solutions at low concentrations, and regional clusters composed of 2-4 water molecules are common and single isolated HBs between water and ether oxygen are also seen at high concentrations.
The detailed method for the generation of atactic polymers with the most probable steric sequences is as follows. First, 1000 configurations of chains, each with 10000 repeat units, are generated as prototypes (we think so many polymer chains with such length are sufficient for the generation of the most probable steric sequences) with the specified steric ratio using the Monte Carlo method. The fractions of the continuous sequences of stereo dyads (such as mr, mmrr, …) are counted, for efficiency only sequences with utmost 4 dyads are counted. The same method is used for the generation of 1000 chains with 44 repeat units, their fractions of the continuous sequences of stereo dyads are compared with those of the prototypes by the root mean squared differences (RMSD), and the chain with the smallest RMSD will be regarded as the most probable configuration with the limited chain length.
This work was supported by the National Science Foundation of China (No. 21304017), the Fundamental Research Funds for the Central Universities and Innovation Program of Shanghai Municipal Education Commission. The calculations in this work were performed in the supercomputing center of Chinese Academy of Sciences. We are fully grateful to the provision of the PVME sample from Prof. Nies in KULeuven.