Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2017) Volume 7, Issue 2
The Mg50Ni45Ti5 alloy for the hydrogen storage is prepared by mechanical alloying. The structure and the morphology of the alloy are characterized by X-ray diffraction (XRD) and scanning electron microscopy (SEM). These techniques esteemed that this alloy is a good candidate for hydrogen storage, since it is both nanocristallin and dsuctile. This is confirmed by the modeling of the hydrogen equilibrium pressure-composition-temperature (PCT) relationships for this alloy. These isotherms were experimentally generated for three temperatures 313 K, 327 K and 340 K and modeled through the statistical physics using the monolayer model with two energies levels. Energetic, steric and thermodynamic studies were released thanks to this model which proved the efficiency and the security of this alloy to the storage of hydrogen.
<Keywords: Absorption energy; Grand canonical ensemble; Hydrogen storage; Mechanical alloying; Thermodynamics
Hydrogen is regarded as the optimist energy vector as it is clean and inexhaustible. The challenge for hydrogen uses is the lack of safety. Its large-scale utilization is mainly hampered by unsatisfactory properties of known hydrogen storage materials. In the past few decades, different kinds of hydrogen storage materials have been developed, such as metal hydrides, complex hydrides, carbon nanotubes and metal organic frameworks (MOF) [1].
Therefore, many intermetallic alloying were used successfully to elaborate some hydrides alloys were developed to solve this problem. Magnesium and magnesium-based alloy are the most promising candidates for hydrogen storage owing to the abundances, non-toxic nature and low cost. Also Magnesium hydride MgH2 is one of the attractive hydrogen storage materials because it is directly formed from the reaction of bulk Mg with gaseous hydrogen and reaches a high hydrogen capacity (7.6 wt. %). However, both the kinetics of absorption and the desorption of pure magnesium are extremely low. Besides, these reactions operate greatly only when applying rather high temperatures, at least above 250-280°C [2]. Numerous attempts have been made to overcome these challenges. Alloying with rare earth metal (La, Nd, Pr) and transitional metal (Ni, Cu) is one of the most commonly employed methods to improve the kinetic properties of Mg based hydrogen storage material [3]. Other reported method to solve this problem by subjecting the powders to long term of ball milling [4]. In fact, long-term of ball milling usually leads to the increase of the influence of grain boundaries and enhance the diffusion of hydrogen [5]. Furthermore, among the benefits of using ball -milling to prepare improved Mg-based materials, we find the ease of formation of several alloys [6-10] and hydride phases [7], the generation of fresh and highly reactive surfaces during the milling operation which intensify the hydrogen absorption rate [9] and the obtainment of Mg-based materials in the nanocrystalline or amorphous state, with various amounts of dislocations and special defects with high binding energy for hydrogen [8,11]. All the investigations suggest that the milled Mgalloys differ greatly in nature from the crystalline ones and the addition of Ni facilitates the absorption and the desorption of hydrogen [12] and decreases the hydrogen sorption temperature. Added to that, some Mg- Ni alloys prepared by mechanical alloying (MA) can absorb or desorb electrochemically a large amount of hydrogen at room temperature [13]. In the present study, the hydrogen absorption performance of nanocrystalline Mg50Ni45Ti5 has been investigated in using the XRD and SEM technique for a morphologic study and in referring to the statistical physics modeling, thanks to model monolayer with two levels of energies, for microscopic and thermodynamic study.
The Mg50Ni45Ti5 alloy was prepared by a mixture of pure magnesium powder (99%), pure nickel powders (99%) and pure Titanium (99%). Then a mechanical alloying was performed at atmosphere with a Fritsch planetary ball milling P6. The vial and the balls used were made from stainless steel and hardened steel respectively. Samples were milled and mixed, under an air atmosphere and at room temperature, for 7 h 25 min. Four balls (diameter=10 mm; mass=4.06 g) have been used with a balls to powder weight ratio equal to 4:1. MA was performed at 400 round/min as a speed. After continuous milling, small amount of the MA powder were extracted from the container for structural characterization by X-ray diffraction. XRD patterns were obtained using a (θ-2θ) Bruker D8 diffractometer with Cu Kα radiation (λ=0.15406 nm). The morphological characterization of the as-milled powders was carried out using (SEM) a Philips XL20 microscope.
The hydrogen storage properties of the mechanically milled powder were evaluated by tracing the isotherm in absorption process. Hydrogen absorption isotherms have been released using the installation presented in Figure 1. It’s composed by a simple cylindrical reactor containing 1 g of Mg50Ni45Ti5. To provide the hot and cold liquids, a thermostat at constant temperature has been used. The delivered water characterized by temperature varies between 20°C and 80°C. The hydrogen used is of the UP type (99.99%). The tank and the reactor are made by stainless steel. The reactor and the tank contain a vacuum ensured by a vacuum pump. The different elements of Figure 1 are bound by stainless tubes via tight stainless valves. The experimental device is instrumented by a pressure pick-up and a chart of acquisition (Agilent) connected to a computer. Before the starting of absorption process, we are kept closed the valves between the hydride reactor on the one hand and the hydrogen tank and receiver on the other hand. During the absorption, hydrogen is supplied from the hydrogen tank.
Structure and morphology of the as-milled powder
The morphology: The morphology of alloy powders mechanically milling for 7 h 25 min is shown in images SEM in Figure 2. We marked obviously a disorder in the microstructure and the alloy is not uniform. Since we have a variety of grain size, the Figure 2a indicates the presence of agglomerates. Their sizes vary between 1500 μm, 667 μm and 500 μm. If we augment the scale, is found in Figure 2b that agglomerates are actually formed by small particles welded together. These particles are of different sizes, as illustrated in the Figure 2d. They vary between 32.5 μm, 26 μm, 6.25 μm and 2.5 μm. Indeed, during the mechanical grinding ball, ductile characteristic of a powder promotes its cold welding as a result of the formation of agglomerates in case of brittle materials fracture is favored [14]. Agglomerates are formed because of the existence of serious inter-granular forces during milling [15]. Also the substitution of Mg based alloys with titanium generally increases their ductility and resistance to corrosion [1,16,17]. So we concluded that Mg50Ni45Ti5 alloy is ductile under the impact of the balls grindings give small particles. Those are accumulated by cold welding. Because of the alloy ductility, repeated deformations induce according to a fatigue mechanism during grinding and the propagation of cracks in the material. Consequently, the Mg50Ni45Ti5 alloy stores a large amount of strain energy. This leads to non stabilization of the lattice, yielding a chemical disordering and a reduction in the grain size. Hence, the final product which is nanocrystalline Mg50Ni45Ti5 retains some of the original chemical order of the crystalline initial intermetallic compound. For the sake of a thorough investigation of the structure and the composition of the experimental substrate, a XRD patterns are released and exploited.
The structure: The overlaid XRD patterns of MgNi45Ti5 alloy (milled 7 h 25 min) are provided in Figure 3. We note the presence of a diversity of sharp reflexion peaks. We have four peaks of Mg2Ni phases, eight of MgNi2 phases and one of Mg phase. This means that 7 h 25 min milling is not enough to dissolve all the elements and to obtain a main phase. Moreover, in Figure 3, we remark the presence of five sharp peaks of TiO2 and one of NiO2. The presence of oxygen implies that the milled material is sensitive to the ambient atmosphere. The large presence of TiO2 is because of the high affinity of titanium for oxygen, hence it dissolves over 30% of oxygen. Actually, titanium is widely used as an oxygen getter [18]. The presence of the NiO2 presents a good agent to hydrogen storage. Since it inhibits the corrosion and protects the Mg from more oxidation [19]. Also the existence of Ni would decrease significantly the discharge capacity of the alloy as the Ni is not a hydrogen storage element [19]. In accordance to the forgoing, the mechanical milling alloy Mg50Ni45Ti5 has a high oxygen sensibility so it shares a good affinity to hydrogen [20]. We can say from the results of XRD and SEM that the powder of Mg50Ni45Ti5 is a good candidate to the storage of hydrogen. The nanocrystalline nature improves the hydrogen absorption properties, in cooperation with the hydrogen diffusion along with the grain boundaries [20]. Not only that but also there is a critical factor for hydrogen absorption which is basically the composition of the metal. This appears capable to disconnect H2 molecules to hydrogen atoms and permit the fast diffusion of hydrogen into the bulk. Since it contains Ni, which is considered as a good agent [19,21] facilities the dissociation of the dihydrogen. Else the presence of the Ti which prevents the alloy corrosion and pulverization [22] is viewed as a good factor for the alloy cycle life during hydrogenation [23-28]. Moreover, the disorder of the structure, as a result of the mechanical milling, is also an agent for the effectiveness of hydriding as it absorbs great amounts of hydrogen at room temperature than its polycrystalline analog does. Furthermore, the standpoint grains size, we have nanosized metal particles. This leads to an extra hydrogen storage and improves the sorption kinetics [29]. In the following part we will try to justify these expectations and to specify the experimental alloy through a statistical scrutiny of the hydride Mg-Ni-Ti-H by the intervention of the grand canonical ensemble of the statistical physics.
Characterization through statistical physics
Figure 4 shows the pressure-composition isotherms measured for three temperatures 313 K, 327 K and 340 K. these isotherms give the quantities of hydrogen absorbed per unit formula. During sorption, the system is considered like an interaction between the absorbate (hydrogen atoms and the absorbent (receptors sites of Mg50Ni45Ti5). The study of particles exchange between the bulk phase and the absorbed phase requires the use of grand canonical ensemble in statistical physics [30] in order to take account of the variation of particle number during the absorption phenomenon. This analysis follows four distinguished parts. Firstly, the supposition of a number of hypotheses is needed for the analysis. Next, the theoretical development of the used adequate model by statistical physics gives the expression of the absorbed quantity per unit formula as a function of the equilibrium pressure of hydrogen. Subsequently, we use the analytical expressions of models to adjust the experimental isotherms so as to choose the suitable model following to a number of criteria. At the end, the parameters given by the adjustment are interpreted and used to characterize the experimental powder.
The assumptions for statistical physics treatment: For steric, energetic and thermodynamic studies, we declare some hypotheses. Initially, the hydrogen is considered as a perfect gas [30-32] supposing that the mutual interaction between the gaseous hydrogen molecules will be ignored. Usually, below the critical pressure (P=13 bar) and higher than critical temperature (T=33 K), hydrogen is an ideal gas [31,33]. This is the case of the experiment for hydrogen (Pexp ≤ 10 bar and Texp ≥ 33 K). Afterward, every hydrogen molecule is characterized by degrees of freedom. These are, specifically, rotational, translational, vibrational and electronic degrees. Each degree of freedom has an energy, which has a characteristic temperature. We ignore all degrees of freedom, we preserve only the translation and the rotation degrees. The characteristic temperature of vibration θv=6215 K [34] is much higher than experimental ambient temperatures so we avoid the degree of vibration of hydrogen molecules. The degree of electronic freedom and nuclear of molecules are frozen [35]. The characteristic temperature of translation is θtr=10-15 K and of rotation is r=85.3 K [34]. Therefore, the translational and the rotational degrees of molecules could be excited at the experimental temperatures 313 K, 327 K and 340 K.
The translational partition function is given as following [33]:
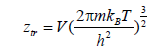 (1)
(1)
V is the volume of the gas, h is Plank’s constant and m is the absorbed molecule mass.
The function of partition of rotation is written the following way:
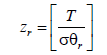 (2)
(2)
Where T is the experimental temperature and σ=2 for hydrogen which is the symmetry number. We assume that a Na number of atoms are absorbed on the Nm sites receptors placed on a unit volume of the absorbent. In fact, the absorption reaction of hydrogen atoms (H) is distinguished by a stoichiometric coefficient n. This reaction is given by the following equation:
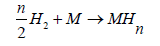 (3)
(3)
H is the hydrogen atom, M represents the receptor site of the alloy (Mg50Ni45Ti5), n is the number of absorbed atoms per site and MHn is the formed hydride.
Theoretical development: For the theoretical development by the statistical physics formalism, we begin by the partition function of grand canonical ensemble. It depends on the temperature T and the chemical potential μ. Therefore, its expression contains the characteristics of the receptor site and the absorbed. That are interpreting after fitting of the isotherms.
This equation is written for a single receptor site as follows [30]:
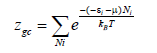 (4)
(4)
Where T is the experimental temperature of the isotherm, μ is its chemical potential, (εi) is the absorption energy of the receptor site, Ni is the number of occupation in the state (εi) and kB is Boltzmann’s constant.
For the Nm receptor sites supposed independent the partition function is calculated by the following equation:
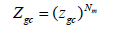 (5)
(5)
The average number of occupation is expressed by [36]:
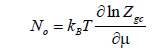 (6)
(6)
Using equation (3), the absorbed quantity is calculated by the following expression [32,37]:
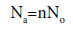 (7)
(7)
Hence the absorbed per unit formula is given in the following equation:
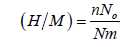 (8)
(8)
Selection of the adequate model of adjustment: In fact, the hydrogen absorption in hydride is monolayer [38], and the released absorption isotherms of Mg50Ni45Ti5 (Figure 4) present a level of saturation. Also the hydrogen absorption in hydride metal is identified by two types of receptors sites [39] and two phases. The experimental isotherms (Figure 4) indicate the presence of two phases the first, at low pressures, contains weak amount of hydrogen and the second, at big pressures, contains large amount of hydrogen. For these reasons, the choice will be a priori outbalance to monolayer with two levels of energies. To more validate this choice, and to make sure that they are no longer useful and then to eliminate any doubt, more general models like a three levels model and monolayer homogeneous model, will be used as a test model.
Heterogeneous monolayer model with two energy levels: We assume that Mg50Ni45Ti5 is characterized by two types of receptor sites. The sites type 1 are characterized by a density Nm1 per unit of volume and by absorption energy (-ε1). The second sites type are characterized by a density Nm2 and absorption energy (-ε2).
The grand canonical partition function for receptor site of type 1 is given by the following equation:
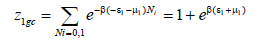 (9)
(9)
The grand canonical partition function for receptor site type 2 is written as follows:
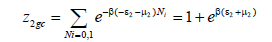 (10)
(10)
The total partition function, supposing that the sites are independent, is given as follows:
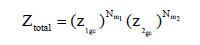 (11)
(11)
The average occupancies are given as follows:
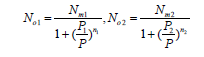 (12)
(12)
We get 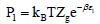 and
and 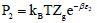 which are the pressures at half-saturations respectively of type 1 sites and of type 2 sites.
which are the pressures at half-saturations respectively of type 1 sites and of type 2 sites.
Accordingly the total absorbed amount is written as follows:
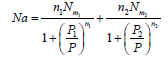 (13)
(13)
Thus, per unit formula the absorbed amount is obtained as follows:
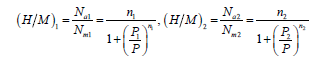 (14)
(14)
Therefore the total absorbed amount per unit formula is:
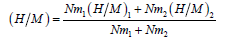 (15)
(15)
Starting from this expression of absorbed amount per unit formula, for a monolayer model with two energy levels, we can fit the experimental isotherms with different temperatures.
Selection of best fitting model: Subsequent to adjustment of the isotherms with the different models proposed previously, the selected model must be in a high correspondence with the experimental isotherms. The choice is based on several criteria in addition to those cited previously (monolayer, proved the presence of two phases and two sites) which justifies priorities and even a posteriori of two levels of absorption energies. Initially, this selection is based on the values of R2 or the values of RMSE. These are calculated by numerical simulation of the experimental isotherms using the microcal software origin version 8. The more the R2 value is close to 1 or the RMSE is close to zero [40], the more suitable the model is. Secondly, the obtained physicochemical parameters must be physically reasonable. The values of R2 and RMSE are indicated in Tables 1 and 2. The monolayer model with tow energy levels has the highest values of R2. Also, its parameters have physically satisfactory values. Hence, we select the two energy monolayer models for the description of absorption isotherms on the alloy of Mg50Ni45Ti5 at T=313 K, T=327 K and T=340 K (Figures 5a-5c).
| T (K) | Hill | Monolayer with two energy levels | Monolayer with three energy levels |
|---|---|---|---|
| 313K | 0.98245 | 0.99476 | 0.99310 |
| 327K | 0.98349 | 0.99204 | 0.99005 |
| 340K | 0.98457 | 0.99419 | 0.99101 |
Table 1: R2 values for the adjustment of hydrogen absorption isotherms in Mg50Ni45Ti5.
| T(K) | Hill | Monolayer with two energy levels | Monolayer with three energy levels |
|---|---|---|---|
| 313 | 0.087 | 0.028 | 0.041 |
| 327 | 0.082 | 0.038 | 0.060 |
| 340 | 0.080 | 0.046 | 0.050 |
Table 2: RMSE values for the adjustment of hydrogen absorption isotherms in Mg50Ni45Ti5.
The obtained physicochemical parameters are presented in Table 3, will be used in the following part to more specify the experimental substrate.
| T (K) | P1 (bar) | P2 (bar) | (H/M)1 | (H/M)2 | n1 | n2 | Nm1 | Nm2 |
|---|---|---|---|---|---|---|---|---|
| 313 | 0.01 | 5.22 | 0.90 | 1.11 | 0.93 | 36.03 | 5.33 | 0.17 |
| 327 | 0.006 | 6.25 | 0.84 | 1.05 | 0.87 | 37.15 | 2.37 | 0.078 |
| 340 | 0.009 | 7.13 | 0.86 | 1.15 | 0.89 | 52.96 | 2.03 | 0.045 |
Table 3: The values of the adjusted parameters of hydrogen absorption in Mg50Ni45Ti5.
Hydrogenation: Hydrogen absorption properties of the nanocristalline alloy Mg50Ni45Ti5 resulting from the mechanical milling are investigated thanks to the six physicochemical parameters given by the adequate model. Firstly, by a microscopic point of view as the number of atoms absorbed per site (n1 and n2) and the density of receptor sites (Nm1, Nm2) per unit of volume. Secondly, by an energetic side as the absorption energy. Finally, by a macroscopic viewpoint as the internal energy, the entropy of absorption, the free enthalpy, the chemical potential, and the free energy.
Microscopic study
Evolution of anchored atoms per site (n1 and n2) with temperature: n1 and n1 are steric parameters. These stoichiometric coefficients appoint the number of hydrogen atoms anchored in site type 1 (M1) in case of n1 and site type 2 (M2) in case of n2. These are expressed in the reaction of absorption the following way:
Absorption in site type 1: 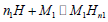 (16)
(16)
Absorption in site type 2: 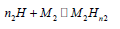 (17)
(17)
Depending on n1 and n2 values we can calculate the anchoring number n’=1/n [41]. We distinguish two possible manners of anchoring atoms. Firstly, for n1, we perceive that it is inferior to the unit the number is between 0.87 and 0.93 atom per site. Thus, one atom can occupy more than one site type 1. Statistically it occupies about 1.07 sites types 1 at T=313 K, 1.14 sites type 1 at T=327 K and 1.12 sites type 1 at T=340 K. Secondly, for n2, we note that it varies between 36.25 and 52.96 atoms per site. In this case the site type 2 is occupied by an agglomerate of hydrogen atoms.
The temperature has a determinant effect on the absorption process and on the arrangement of the atoms in the absorbent. The variation of n1 and n2 with respect to temperature are plot depicted respectively in Figures 6 and 7. Foremost, by increasing temperature, n1 (Figure 7) admits two behaviors. This number decreases from 0.93 atoms per site type 1 at 313 K to 0.87 at 327 K and then it increases until 0.89 atoms per site type 1 at 340 K. For n2, the greater the value of temperature is, the bigger n2 is. The increase of n1 and n2 is appropriate to the thermal agitation. All this accelerate and might promotes the anchoring of hydrogen atoms in sites type 1 and 2. Moreover in increasing the temperature, the rate and the kinetic of oxidation augment [42]. It is the same behaviors for the TiO2 [43]. Hence, the rise of n1 and n2 with temperature can be explained by the blockage and the colonization of the sites with impurity (oxidation). The antagonistic behavior (the decreases of n1), it can be explained by the increase of the inter-atomic distance in the alloy. Where the increase of temperature by 14 K (from 313 K to 327 K) causes the increase of the average distance between the atoms of substrates. Hence, new sites types 1 are created and collaborate in the absorption process. Also the decrease of this parameter can be explained by the activation of deep trapping sites for the hydrogen [42]. Moreover, the presence of a large number of grain boundaries and surface defects due to mechanical grinding would facilitate the diffusion of hydrogen in the matrix. This can be more effective with the increase of temperature. Consequently, n1 decreases.
The behaviors of these parameters (n1 and n2) versus temperature are mostly explained by the behavior of Nm versus temperature, since these two parameters are inversely proportional.
Variation of receptor sites densities Nm1 and Nm2 according to temperature: The nanocrystalline nature improves the hydrogen sorption properties, thanks to enhanced hydrogen absorption and diffusion along grain boundaries [44]. During the mechanical grinding, the alloy had undergone many repeated mechanical deformations. Hence, the powder particles create a variety defects in the initial structure of the crystallites as dislocations, vacant sites, stacking faults and increased grain boundary. Thus, the hydriding properties are improved. The improvement was due to a cooperative effect of all these structural defects. They allow the appearance of several sites that promote the absorption of hydrogen in the solid matrix of Mg50Ni45Ti5. These sites are divided into two categories referring to the adequate model. These two categories are sites type 1 and sites type 2 characterized by their density per unit volume Nm1 and Nm2 respectively. The variations of the density of these two types of sites according to temperature are plotted in Figures 8 and 9.
These steric parameters are directly linked to the absorbed amount per unit formula and the number of hydrogen atoms absorbed at the saturation as expressed by the following equations:
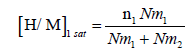 (18)
(18)
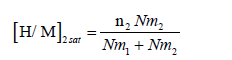 (19)
(19)
For the two types of sites when temperature rises, as it is presented in Figures 8 and 9, this these parameters decrease. For Nm1 (Figure 8), it diminishes from 5.33 (sites/unit of volume) for T=313 K to 2.038 (sites/ unit of volume) for T=340 K. For Nm2 (Figure 9), it decreases from 0.16 (sites/unit of volume) for T=313 K to 0.04 (sites/unit of volume) for T=340 K. This behavior is the result of the thermal agitation, since the later causes the destruction and/or the blockage of some sites. Also by increasing temperature the oxidation rate raises [42,43] hence receptors sites can be occupied and blocked by these impurities. This behavior can be explained by the buildup of n2 hydrogen atoms agglomerate (Figure 7) with the increase of temperature. This agglomerate may be preventing the anchorage of hydrogen atoms to these receptor sites, so their receptor sites appear inactive. Likewise, this accumulation of n2 aggregate generates a volume expansion which creates the pulverization of the Mg50Ni45Ti5 matrix. The more intense the pulverization is, the biggest the destruction of the sites type 2 is. Therefore, Nm2 decreases.
Variation of (H/M)1 and (H/M)2 according to temperature: The saturation absorption quantity per formula unit depends on the number of molecules per site and the density of receptor sites. Hence it is expressed by the previously equation (18) and (19). It tells us about the capacity of Mg50Ni45Ti5 at storing hydrogen atoms per unit formula at saturation state. The influence of the temperature on the two absorbed amounts at saturation for both site types (type 1 and 2) are illustrated in Figure 10. We notice that as the temperature increases [H/M]1 sat and [H/M]2 sat vary slightly. These are almost unchanged. This capital that globally at such a limited range of temperature, thermal agitation resulting from the effect of temperature hasn’t almost any effect. This is a strong point of the model since the absorption capacity at saturation expressed by the analytical expression (eqs 18 and 19) does not already depend on temperature. However, this is owing to the truth that absorption is a chemical absorption which means that energy leads to electronic interactions upon, which temperature has no effect since the electronic features of temperature are very higher than the ambient one. Indeed, the total saturation absorption quantity per unit formula doesn’t depend on the temperature but to diverse other factors. It’s rather related to structural transformations. This parameter is enhanced by the creation of fresh and highly reactive surfaces upon the mechanical milling, the presence of a large number of grain boundaries and surface defects [45]. In addition, the nanosized metal particles leading to extra hydrogen absorption [29]. However, this parameter is inhibited by impurities in the milling atmosphere, particularly the oxidation, like for example, the TiO2 and NiO2 (Figure 3) [19,20]. This latter may explain the slightly decrease in the total saturation absorption quantity per unit formula.
Variation absorption energies according to temperature: The study of the energetic aspect of the hydrogen storage process is very important. It clarifies the hydrogen retention mechanism at the absorption phenomenon. In this part, we interest in the study of the adsorption energy variation depending on the temperature (Figure 11). Absorption energy is defined when hydrogen atom is anchored on the receptor site. This energy is especially at equilibrium, which is a characteristic of an isotherm. There are two absorption energies, one for the site type 1 and the other for the site type 2. these are calculated in the following expressions [36]:
For the site type 1: 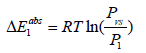 (20)
(20)
For the site type 2: 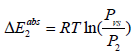 (21)
(21)
P1 and P2 are the pressures at half saturations for the sites type 1 and type 2, respectively. And Pvs is the saturated vapor pressure. Generally speaking, it has been speculated that the hydrogen movement could be characterized by two separate processes, quick and slow way, corresponding to two types of interstitial sites [40]. Both procedures imply the presence of two energy levels. This is another argument accentuating the choice of the heterogeneous model monolayer as adequate model. The absorption energy values (Figure 11) showed that the phenomenon is a chemical absorption, since the different values were more than 40 kJ/mol [46]. It is an irreversible phenomenon [46] this criterion makes the storage of hydrogen in the powder of Mg50Ni45Ti5 a secure method. The change in energy as a function of temperature is plotted in Figure 11. We observed that the absorption phenomenon starts with filling the sites type 1 since their energies are higher than those of the sites type 2. Hence, the hydrogen motion is characterized by two separated process, the first is a fast one marked by the highest absorption energy which is ΔE1abs and the second is a slow one characterized by the lowest absorption energy ΔE1abs .
Also we can obviously notice that the absorption energies ΔE1abs and ΔE1abs rise with temperature. This behavior can be attributed to the thermal agitation. In effect, absorption energy is an energy level of vibration in the well potential of lennard-Jones. If temperature increases the equilibrium energy is also increased.
Also we can conclude that the sites types 2 are trapping sites, as they have the lowest absorption energy [42]. However, those types 1 are very active sites generated during the mechanical milling by the creation of active surfaces. In spite of the highest absorption energy ΔE1abs , sites types 1 absorb only a fraction of hydrogen atoms. Thus, we can confirm that the site type 1 is smaller than the hydrogen atom size. While the site type 2 has a very large pore size, since it absorbs a lot of hydrogen atoms (agglomerate) despite its lowest absorption energy ΔE1abs Hence, owing to those weak densities per unit volume Nm2, we can confirm that the Mg50Ni45Ti5 has a lower porosity, which is a criterion of alloys based of Mg [17].
Thermodynamic study: With reference to the statistical physics, we can translate from the microscopic to macroscopic behaviors of physical systems. Thanks to statistical tools, we can relate the properties of a macroscopic system to the behaviors of its individual elements, and in that way we obtain a better understanding of both. This study of interrelationships among macroscopic properties is called thermodynamics. The thermodynamic study of the absorption phenomenon allows us to characterize macroscopically the Mg50Ni45Ti5 alloy and its hydrogen atoms absorption. This macroscopic study is realized by means of different thermodynamic potential as the internal energy, the absorption entropy, the free enthalpy, the chemical potential and the free energy.
Internal energy: Internal energy represents all forms of energy in the system. It encompasses the relative motion and interaction among only the system’s own particles [47]. We will focus, especially, on the existing interactions between absorbate and absorbent [32].
Generally speaking, the internal energy is given according to the following expression [48]:
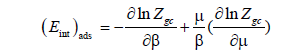 (22)
(22)
In the case of the heterogeneous monolayer model with two energy levels, the internal energy has the following formula:
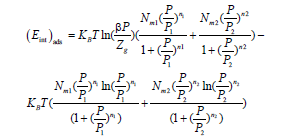 (23)
(23)
Figures 12 and 13 plotted the variation of internal energy with pressure. It is a negative energy int ΔE , hence at absorption the system releases energy. This release of energy denotes that the system evolves spontaneously and emphasizes the idea that absorption is an exothermic phenomenon. Also we can say that this result supports the fact that the interaction between the absorbent and the absorbat is an attractive interaction. If the interactions, in a system, are predominantly attractive then ΔEint is negative [47].
hence at absorption the system releases energy. This release of energy denotes that the system evolves spontaneously and emphasizes the idea that absorption is an exothermic phenomenon. Also we can say that this result supports the fact that the interaction between the absorbent and the absorbat is an attractive interaction. If the interactions, in a system, are predominantly attractive then ΔEint is negative [47].
Adsorption entropy: This thermodynamic potential provides an overpass between the macroscopic and the microscopic level, as it appoints an atomic disorder or chaos prevailing in the system. Since, the entropy for macro-state of a given system is a measure of the number off all possible microstate accessible to the system. Then the larger the possibility of microstates is, the bigger the disorder is. We obtain a state of vanishing entropy [49] if the system has only choice, to be in a unique state. Hence, the order predominates. Using the adequate model we establish this function’s expression. Firstly, we start from the grand potential J and the total grand canonical partition function Zgc. Secondly, according to the total energy of absorption and to the chemical potential μ, we obtain [50]:
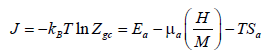 (24)
(24)
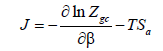 (25)
(25)
kB is the Boltzmann’s constant equals to 1.38 × 10-23 J.K-1.
Then the entropy is deduced, and it is written as follows [33]:
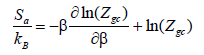 (26)
(26)
Finally, the configuration entropy of the heterogeneous monolayer model is determined in the following expression:
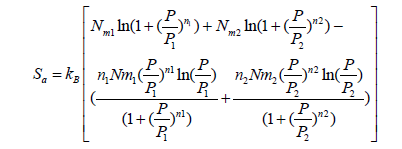 (27)
(27)
Figure 14 shows the variation of the configuration entropy in relation to pressure at T=313 K, T=327 K and T=340 K. We notice that the entropy has two different behaviors characterized by the presence of two peaks. The first peak is greater than the second. The first one, the greatest, is located at P=0.01 bar for T=313 K, at P=0.006 bar for T=327 K and P=0.00916 bar for T=340 K. The second, the weakest, is positioned at P=5.22 bar for T=313 K, at P=6.25 bar for T=327 K and at P=7.13 bar for T=340 K. Comparing these values to those given by the fitting, we conclude that peaks are close to pressures at half saturation for the sites types 1 and those types 2, P1 and P2 respectively. We can declare that before the half saturation of the sites types 1, the entropy increases rapidly. This implies that disorder rises rapidly because the hydrogen atoms have a many configurations since the majority of sites are empty. After half saturation of these Nm1 sites, for pressures superior to P1, the entropy diminished to a weak values. This implies that order predominates in theses Nm1 sites. We can affirm that the number of configurations diminished as we get closer to saturation of these sites. As long as the hydrogen is anchored the disorder diminishes. Until the disorder‘s decrease of sites type 1, absorption entropy of the Nm2 sites types 2 will slightly increase up to P2, then it decreases. Hence we conclude that the absorption in sites 2 has started after a delay of pressure in comparison to sites type 1. This is also demonstrated previously by the energetic study. As it is mentioned above for site type 1, below the half saturation, hydrogen atoms have many configurations to anchor in sites type 2. Hence they are jostled to occupy these sites so the disorder increases. Above half saturation, most of hydrogen atoms are absorbed so the order dominates.
Free enthalpy: Absorption is marked by the liberation of heat, evolving to a lower energy state. So it evolves to a more thermodynamically stable state. Therefore, absorption is a spontaneous process [51,52]. In this context, we intend to improve this truth by our adequate model, with checking the free enthalpy behavior versus temperature. The free enthalpy is a thermodynamic potential which allows defining the orientation of reaction and its positioning at equilibrium. If ΔG<0, the system develops spontaneously. But if G<0, the system is at equilibrium. It is given in the following relation:
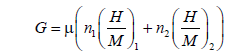 (28)
(28)
μ is the chemical potential given by the following equation:
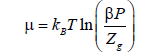 (29)
(29)
Zg is the partition function of hydrogen at gaseous state. It is expressed by:
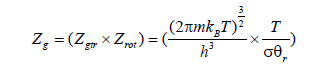 (30)
(30)
Using our model and the eq.28 we can introduce the free enthalpy as follows
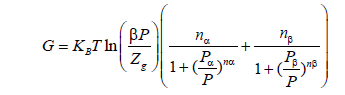 (31)
(31)
We notice from the Figure 15, that the free enthalpy decreases with pressures at the three temperatures. It varies with pressure according to four regimes. Firstly, The free enthalpy decreases for low pressures around the pressure of half-saturation of site type 1. In this interval, hydrogen atoms are spirited to be absorbed in sites type 1 and the absorbed amount increases. In this case it is possible to say that absorption in sites type 1 evolutes spontaneously. Secondly, for pressures more superior to the pressures at half-saturation of sites type 1, ΔG ≈ 0 this means that these sites are saturated and reach equilibrium in this interval of pressure. Thirdly, by more increasing the pressures and getting more closer to the half-saturation pressures of sites type 2,
The free enthalpy decreases for low pressures around the pressure of half-saturation of site type 1. In this interval, hydrogen atoms are spirited to be absorbed in sites type 1 and the absorbed amount increases. In this case it is possible to say that absorption in sites type 1 evolutes spontaneously. Secondly, for pressures more superior to the pressures at half-saturation of sites type 1, ΔG ≈ 0 this means that these sites are saturated and reach equilibrium in this interval of pressure. Thirdly, by more increasing the pressures and getting more closer to the half-saturation pressures of sites type 2, Thus, the absorption in sites type 2 has started and it’s a spontaneous process. Finally, for the pressures higher than the half-saturation pressures of sites type 2, the ΔG=0. This means that equilibrium is reached when saturation is reached. Therefore, we can say that hydrogen absorption in Mg50Ni45Ti5 is a spontaneous process, where a decrease of the free enthalpy is observed. More exactness, at the level of sites, the free enthalpy, in absolute value, of the sites type 1 is less than this of type 2 one. So we can confirm the fact that site type 1 is more stable than type 2 one. Since, as it is pointed out previously the sites type 1 start firstly absorbing the hydrogen atoms given that thermodynamically atoms or molecules tend to adopt the structure with the lowest free enthalpy [51-53].
Thus, the absorption in sites type 2 has started and it’s a spontaneous process. Finally, for the pressures higher than the half-saturation pressures of sites type 2, the ΔG=0. This means that equilibrium is reached when saturation is reached. Therefore, we can say that hydrogen absorption in Mg50Ni45Ti5 is a spontaneous process, where a decrease of the free enthalpy is observed. More exactness, at the level of sites, the free enthalpy, in absolute value, of the sites type 1 is less than this of type 2 one. So we can confirm the fact that site type 1 is more stable than type 2 one. Since, as it is pointed out previously the sites type 1 start firstly absorbing the hydrogen atoms given that thermodynamically atoms or molecules tend to adopt the structure with the lowest free enthalpy [51-53].
The free energy: This thermodynamic potential describes the attitude of the system to execute work isothermally. It is expressed by the following equation [54].
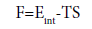 (32)
(32)
It is thus the free energy while TS is called the bound energy or the isothermally unavailable energy [55]. When absorption is achieved, in Figure 16, the free energy F takes negative values. It decreases, at the three experimental temperatures, with increasing the pressure. This asserted that absorption proceeds spontaneously. This decrease is also equals to the amount of works delivered by the hydrogen atoms, at constant temperature, to be absorbed in sites types 1 and 2. This behavior explains that as the free energy is lowering as the energy barrier is minimized then simply the absorption of hydrogen atoms is thermodynamically fasters. It is quite impressive to the absorbed quantities (H/M)1 and (H/M)2 since they can be huge rapidly and the saturation is obtained [56]. We remark also, that the free energy of the site type 1 is higher than that of the type 2 one (Figure 17). Then, we admit that the site type 1 is an inconvenient one. It absorbs just small quantities [56], as it is already stated thanks to this adequate model (Table 3).
We conclude that the mechanical alloy Mg50Ni45Ti5 is a nanocristallin alloy able to chemisorbed hydrogen spontaneously and exothermally. For this reason MA alloy the increase in temperature has a slightly effect at the total stored hydrogen amount. This MA is characterized by two receptor sites. The site type 1, with a high density Nm1 per unit of volume which absorbs n1 fraction of hydrogen atoms, although it has the highest absorption energy. The second type is site type 2, distinguished by its low density Nm1. In spite of its absorption energy which is less than such of the type 1 one, it storages n1 agglomerate of hydrogen atoms. Due to the entropy of absorption, we find that the site type 1 is faster and absorbed firstly hydrogen atoms than the type 2. According to the free enthalpy, we can confirm that the site type 1 is more stable than type 2. Not only that but also, the free energy tells us that the site type 1 is an unfavorable site for the hydrogen storage function since its free energy is higher than that of the type 2. it is logical to admit that this search leads us to agree that the MA Mg50Ni45Ti5 can be a helpful material for hydrogen storage in large scale thanks to its rapidity, security, easy (at ambient temperature) absorption process and the diversity of its sites.