Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
+44 1478 350008
ISSN: 2161-0398
+44 1478 350008
Review Article - (2014) Volume 4, Issue 5
We discuss the implementation of a multiscale biophysico-chemical model able to cope with the main mechanisms underlying cumulative exocytosis in cells. The model is based on a diffusion equation in the presence of external forces that links calcium signaling and the biochemistry associated to the activity of cytoskeletal-based protein motors. This multiscale model offers an excellent quantitative spatio-temporal description of the cumulative exocytosis measured by means of fluorescence experiments. We also review pre-existing models reported in the literature on calcium waves, protein motor activation and dynamics, and intracellular directed transport of vesicles. As an example of the proposed model, we analyze the formation of the shield against polyspermy in the early events of fertilization in sea urchin eggs.
<Keywords: Calcium wave; Protein motors; Biochemical energy landscape; Diffusion
Biological processes frequently involve several mechanisms and sub-processes that link different temporal and length scales such as, for example, intracellular molecular interactions to the scale of cells and beyond to the behavior of collectives of cells and even organisms [1]. From an applied point of view, biomedical research often performs experiments in which these scales are also imbricated [2]. The quantitative modeling of these systems and the processes they perform often requires the extensiveuse of computational simulations that have to incorporate several simulation techniques, each one according to the time and space scale associated to the biological process in question [3].
However, simple theoretical models able to cope with these problems are less developed in the literature, although they may be of great importance because they can simplify the quantitative description without loss of accuracy and, more important, by allowing to give clear interpretations of the different mechanisms in terms of simple and well understood physicochemical laws.
In this short review, we aim to describe, link and use three theoretical models reported in the literature that allow to formulate a theoretical multiscale model able to cope, with high precision, with intracellular processes involving exocytosis, that is, with the process by which a cell directs the contents of secretory vesicles out of the cell membrane and into the extracellular space. We look at this particular biological process due to its ubiquity and biomedical importance ranging from transcelular transport, insulin, neurotransmitter and enzyme secretions in the energetic, nervous and early developmental metabolic processes and pathways [4]. In particular, we will study the case of the early events of fertilization, that is, the formation of the shield against polyspermy in oocytes (Figure 1).
Figure 1: Scheme showing the three main mechanisms associated to the initial events of oocyte fertilization. Sperm entry through the acrosomic reaction liberates the genetic material into the oocyte and triggers the local entrance of external calcium and the subsequent propagation of a calcium wave through the ooplasm. This process activates protein motors, that actively transport clusters of cortical vesicles towards the plasmatic membrane. Once fused, hyaline is released and initiates the gradual activation of the vitaline envelope until the shield against polyspermy is completed.
Exocytosis is a very broad and complex process that involves different sub-processes such as the formation and storage of vesicles in different pools inside the cell, the calcium signaling process, the active transport, and other related processes such as vesicle docking, priming and the final fusion of the vesicle in the porosomes of the plasmatic membrane [5,6]. Many of these processes have been studied experimentally and, as a consequence, several proteins and enzymes have been discovered. However, beyond the knowledge of their existence and participation, there is still a fundamental lack of understanding concerning the specific role they play in the secretion process [7].
Depending on the particular physiological function of the exocytosis in each cell type, there are variations in the rate of exocytosis, the lag time before it begins, its time course, the proportion of vesicles that undergo fusion in response to stimulation, the presence of single or multiple granule types, and the nature of the regulation of exocytosis by second messenger pathways [8]. Forexample, in the particular case of fertilization of urchin sea eggs, the exocytotic process involves sperm fusion with cell membrane, the influx of external calcium and the subsequent elevation of calcium concentration due to the internal pools. Subsequently, other fundamental processes take place like the formation and storage of cortical granules, the docking, priming and fusion of the secretory vesicles with the plasma membrane, presumably through SNARE proteins. Finally, the formation of the vitaline envelope and the final endocytosis and recycling of empty vesicles are processes that may play an important role in regulating the exocytosis [9].
The presence of micotubules and actin filaments may play opposite roles depending on the cell type. In some cases, the excytosis becomes favored by the presence of the cytoskeleton, as in the case of serotonin and hyaline secretion [10], whereas in other cases it may be inhibited by the presence of the cytoskeleton that acts as a mechanical barrier [11,12]. Presumably, cytoskeleton based secretiondepends on the action of protein motors whereas the opposite case suggest a diffusion controlled exocytosis [13]. The distances travelled by the secretory vesicles in both cases are very different. In this review, we focus on the first case, that is, in which secretion is mediated by cytoskeleton associated protein motors. Therefore, for the particular case of the urchin sea fertilization, we have considered calcium signaling, vesicle diffusion and protein motor activation and its processivity as the rate controlling steps in the secretion process.
An appropriate measure of the cumulative exocytosisby release site can be performed with the help of fluorescenceexperiments [10,14,15]. In these experiments, a fluorescent dye is dissolved in the culture medium in such a way that it is activated when becomes adsorbed in the plasma membrane and is illuminated with the appropriate light. During secretion, intracellular vesicles fuse withthe plasmatic membrane to release its contents. Exposed to the culture medium, the membrane of the vesicles adsorbs the dye and increases the local fluorescence.
In view of this, the theoretical description of cumulativeexocytosis is based on an apparently simple model.The main question is to know the number of vesicles that arrive to a given release site of area A in the membrane and fuse with it as a function of time. Therefore, if J(t) counts the number of cortical granules per unit area thatreach the release site at the membrane per unit time, then the number n(t)of fused cortical granules as a functionof time is given by the relation
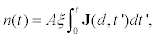 (1)
(1)
where A is the measure area and d the initial positionof the vesicle cluster with respect to the plasmatic membrane [15]. The fusion efficiency parameter ξ is the fraction of vesicles that release its content with respect to the total number of vesicles arriving at the plasma membrane. Here, for simplicity, we will assume that thisparameter is the unity. In principle, this simple model quantifies the cumulative exocytosis observed in experiments [14,15].
However, it is clear that the current J(t) must be determined explicitly in order to make a quantitative progress. Determining J(t)is not a trivial task. The mechanism ofthe secretion of the vesicular contents out of the cell isa complex process that involves calcium signaling, activation and action of several cytoskeletal motors through distances typically involving few microns. This is an energy consumption process due mainly to the activity ofthe protein motors and pumps. Therefore, this makes very important to consider the detailed description ofthe dynamics and energetics of these entities.
In fact, in order to obtain J(t) and perform the program outlined, one needs to formulate a multiscale model that accounts for the initial events of fertilization. In particular,we have to reproduce the reaction-diffusion wave propagation of internal and external calcium and coupleit with a directed diffusion model describing the transport of granule clusters containing hyaline to the plasmamembrane. This second step considers in parallel the biochemical kinetics of protein motors, kinesins, myosins and dyneins [16]. As a consequence, our work gives quantitative evidence that the long time enzyme secretion of cortical vesicles or granules is driven by protein motors, mostly by kinesins.
The paper is organized as follows. In Section 2 we review previous theoretical works on reaction-diffusion calcium signaling; protein motor biochemistry, energetics and dynamics; and finally on diffusion in the presence of external forces, that allow to propose an unifying view of the exocytotic processes from the a physical chemistry point of view. In Introduction we apply the multiscale model to describe the slow formation of the shield against polyspermy, which occurred when exocyted vesicles lift the viteline envelope away. In particular, we join the results of the pre-existing models on calcium waves, protein motors activation and intracellular directed transport of vesicles in a cell for a successful quantification of cumulative exocytosis previously reported in experimental data. Finally, Review of Theoretical Background is devoted to present our main conclusions.
As we have already mentioned, the exocytosis of substances by cells comprise several mechanisms whose interplay is essential. This interplay links several time and length scales that should be modeled in a nested way. Looking at the events, the entrance of external calcium into the cell through the corresponding ion channels and its interaction with the intracellular calcium is the triggering one of subsequent processes, like activation of cytoskeletal-based protein motors and their active transport of vesicles and granules towards the plasmatic membrane along microtubules. Here, we review previous theoretical work reported on these three main processes. In order to fix ideas, we will discuss the general aspects of the three models by considering the phenomenology associated to the fertilization of sea urchins eggs. This may help the reader to create a clearer image of the secretion process and the mechanisms involved.
Locally-constrained and directed diffusion
The mechanisms participating in exocytotic processes that we already discussed, calcium wave signaling and protein motor action converting chemical energy into mechanical one, can be linked by means of a diffusion model in the presence of external forces. Because this diffusion equation is very general, we will first discuss it in order to show where the other mechanisms enter.
Mass transport inside cells is always affected by thermal agitation that induces a diffusive motion. This diffusion is more or less important depending on the external forces acting over the transported bioparticles. In addition, the intracellular medium consists of a wide variety of polymers and organelles whose presence causes a viscoelastic behavior of the cytosol which, in principle, should be taken into account [17]. As a consequence of this, when bio-particles undergo different forms of passive diffusion in the intracellular medium they often show anomalous diffusion (subdiffusion) [18,19].
Subdiffusion has been observed in the passive transport of particles in the cellular medium whereas an enhanced diffusion has been reported for particles driven by protein motors [20]. This enhanced diffusion was analyzed in terms of a generalized diffusion equation containing forces due to the cytoskeleton network and to the protein motors [10,13,21]. However, when protein motors carry bio-particles of different sizes, this anomalous diffusion is sometimes weak and normal diffusion can be used to describe the motion with an effective diffusion coefficient.
Local confinement and protein motor action are therefore the key ingredients to explain vesicle transport in cumulative exocytosis [10,21].
Let us consider ρ(x, t) as the number of transported vesicles per unit volume and Dν is the diffusion coefficient of vesicles in the cytoplasm. Then, the time evolution of ρ(x, t) is described by the general equation
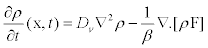 (2)
(2)
whereF is a vector which represents the total force overthe transported vesicles and β is the friction coefficient of the transported vesicles. Here, it has been proposed that force F could be a combination of harmonic radial forces [10,13,21]: 1) a locally constraining force that keeps the vesicles fixed to microtubule an 2) a pulling force due to the activity of molecular motors. Thus, the first force can be modeled as resulting from a local harmonic force F=– w2x which is applied simultaneously with the force of the motors that move with velocity v [10,21,22]. The total force applied on the vesicles is an harmonic force displacing in the same direction as the molecular motors with velocity v(t).As a consequence of this, it may be modeled by means of the relation
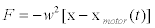 (3)
(3)
Where xmotor (t) represents the position of the motor as a function of time [10,22]. Hence, if the protein motor velocity is, in general, time dependent, then the force takes the form
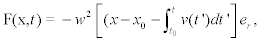 (4)
(4)
Where xo is the initial position of the transported vesicles with respect to the release site. In writing Equation 4, we have supposed that: 1) mobilization of motor does not occurred until some critical time t0 when local Ca2+ has reached some critical value; 2) before its activation, kinesin exerts a trapping force–w2(x–x0) over the vesicles,and 3) once activated, the movement and influence of the kinesin is only radially outward, being er the outward unity vector. Calcium waves and the biochemistry of molecular motors, that will be discussed in the following subsections, allow to determine an explicit expression for the average motor velocity v(t) and its activation time. In general, we may assume that the process starts instantaneously when there exist saturation levels of ATP and local Ca2+ concentration increases over a threshold value. This situation can be taken into account through a Heaviside function in the form 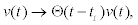 where ti depends on time and position through Ca2+ concentration.
where ti depends on time and position through Ca2+ concentration.
Inserting Equation (4) in (2), one can find ρusing the appropriate initial and boundary conditions. The experiments suggest that one may use three distinct pools of vesicles as initial condition [14]: one very near membrane, other in the center of the cell and one in intermediate position. As a boundary condition, one may suppose that vesicles reaching the membrane fuse to the plasmatic membrane at the same rate at which they arrive.
From the previous equations, we can know the number of cortical granules that reach cell membrane during exocytosis. To obtain this quantity, one must calculate the current of vesicles J(x,t) implicitly defined by the conservation equation ρt= ∇ .J.Direct comparison with equation (2) reveals that the current is given by
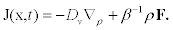 (5)
(5)
Since we are interested in cumulative exocytosis, we need to sum each vesicle arriving to the membrane as a function of time. If J(d,t) counts the density of cortical granules reaching the membrane from the initial position d of the cluster, then the number n(t) of fused vesicles is given by the relation (1).
As we have mentioned above, we need now to determine the time at which the motors are activated and the time dependence of the molecular motors. In order to see how this can be done, in the following subsections we will discuss the role and phenomenology of calcium waves and signaling, and of the biochemistry and dynamics of the molecular motors.
Calcium waves
Two main models are widely used to explain intracellular oscillations and waves: 1) the calcium induced calcium release model (CIRC) and 2) the two-pool model (TPM). Both models are based on reaction-diffusion equations for the Ca2+ concentration and one for the calcium stored in the internal reservoirs  . The election of the model should be based in accordance with cell type and the kind of stimulation. By solving these models with the appropriate boundary condition, one obtains the spatio-temporal behavior of the
. The election of the model should be based in accordance with cell type and the kind of stimulation. By solving these models with the appropriate boundary condition, one obtains the spatio-temporal behavior of the  concentration.
concentration.
Inside the cells, after the external stimulation, oscillationsof the calcium concentration produce spatial non homogeneities along the cell. These non-homogeneitiesseem to induce a spatio-temporal organization of cell’s activity, that is, calcium waves act as a signal starting different processes at different times and positions, and is a function of the initial stimulation.
In vertebrates, the Ca2+ is mainly stored in bones, from where it may be released to the blood after the adequate hormonal stimulation. Inside many types of cells, Ca2+ it is stored mainly in the endoplasmatic reticulum.
This allows to use it when necessary. Intracellular Ca2+ concentration is lower than the extracellular one, 0:1 μM and 1μM, respectively. This implies that the entrance of Ca2+ through the corresponding ionchannels after membrane depolarization is an spontaneous irreversible process. This means that no energy is necessary to add in order to perform this entrance. After the response of the cell to the stimulation is completed, molecular pumps regulate again the Ca2+ concentration inside the cell.This one is an energy consuming process which is necessary because Ca2+ may be toxic for high concentrations in blood and cells.
Specifically, the Ca2+ is removed from the cytoplasm in two ways: 1) pumping it out of the cell and 2) pumping it inside several organelles like the mitochondria, the endoplasmic reticulum (ER) or the sarcoplasmic reticulum (SR). Thus, during the initiation and the propagation of a calcium wave, the influx of Ca2+occurs in two ways: 1) the entrance of extracellular calcium and 2) the release of calcium from the internal reservoirs.
The two internal calcium reservoirs are activated by two types of receptors: ryanodine and IP3. With the attachment of these receptors on the membrane, the ion channels open allowing the release of calcium to the cytosol. Ryanodine is more common in neurons and pituitary cells whereas IP3 is mainly found in non-muscular cells.
Calcium-induced calcium-release model: The calcium-induced calcium release-model (CIRC) was originally proposed by Friel [23] and it is more frequently use in ryanodine dependent processes. The CIRC model is based on a balance of Ca2+ fluxes in the cell as it is shown in figure 2. A single internal reservoir (ER) exchanges Ca2+ with the cytosol through the fluxes JL2 and JP2. The cytosol, in turn exchanges calcium with the extracellular environment with the fluxes JL1 y JP1. Denoting the calcium Ca2+ concentration in the cytoplasm by c and cs the calcium concentration in the internal reservoir 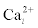 , the model postulates the following dynamics (Figure 3)
, the model postulates the following dynamics (Figure 3)
Figure 2: Sample traces of exocytosis in eggs for different external calcium concentrations. For each series, the number of newly emerged exocytosis disks in each image frame was counted. This number plus the numbers from all previous frames gave the cumulative number for this time point. Each line correspond to different values of external calcium: 0.4, 2 and 10mM for blue, orange and green points respectively. For fitting we use β = 1x10-6s-1, ω = 223.6s-1 in equation (2). Other parameters appear in the box inside the text.
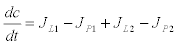 (6)
(6)
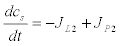 (7)
(7)
where the fluxes depend on the concentrations in the following way:
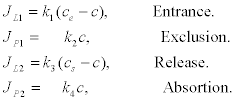 (8)
(8)
Here, ce is the external Ca2+ concentration that may be assumed as constant due to the large concentration difference. However, because a linear model do not leads to the concentration instabilities responsible for the appearance of waves and oscillations, it is assumed that the reaction rate k3 depends in a non-linear way on the cytosolic calcium c in the form
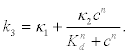 (9)
(9)
This simple model provides an excellent quantitative descriptionof experimental cytosolic Ca2+oscillations andtheir periods, and predicts the observed flows in each cycle [23].
The two-pool model: The two-pool model, originally proposed by Goldbeter [24], suggested the existence of two calcium reservoirs that are activated in series by different agonists. Specifically, the first reservoir is sensitiveto IP3 whereas the second one is sensitive to Ca2+. The second pool performs a CICR-exchange process with the extracellular medium, see Figure 4. Several peculiarities of calcium dynamics for different cellular types can be successfully reproduced using this model [24].
As in the CICR model, a calcium flow balance between pools and the exterior is performed. However, in this case, the fluxes are given by non-linear relations that are determined independently in the experiment. The important assumption of the model is that the calcium concentration in the first pool (sensitive to IP3) is constant during the whole process. Thus, as in the CICR model, only the cytosolic calcium concentration and the concentration inside the second pool cs change with time.
Hence, assuming also that the IP3 gives rise to a constant Ca2+fluxr, and that the calcium is pumped to the extracellular medium with rate–kc, then the whole dynamics is given by
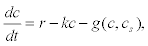 (10)
(10)
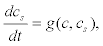 (11)
(11)
Where g(c,cs) represents the rate of change of Ca2+ in the second pool that depends on the uptake and release flows.
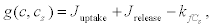 (12)
(12)
Where
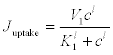 (13)
(13)
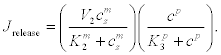 (14)
(14)
Here, Juptake is the rate at which the Ca2+ is pumped towards the second pool, that is, by means of an active mechanism, and Jrelease is the rate at which calcium is released from this second pool. This is an active feedback mechanism for the Ca2+ that is essential for the appearance of calcium oscillations in the cytosol. Finally,  is the rate at which the calcium is released to the extracellular medium. The exponents l, m and p and the other parameters should be chosen appropriately for each case.
is the rate at which the calcium is released to the extracellular medium. The exponents l, m and p and the other parameters should be chosen appropriately for each case.
Calcium waves and the two-pool model: Frequently, Ca2+ oscillations do not occur in an homogeneous way inside the whole cell. On the contrary, these oscillations are organized spatially in the form of waves. The velocity of these waves is notably similar in many different types of cells (5-20 μm/s). In general, these waves are independent of the extracellular calcium and they are often concentric, plane or even have a spiral shape. The utility of these waves can be attributed to the intracellular-extracellularcommunication.
In order to model these waves, it is assumed that the cytosolic calcium c diffuses, and therefore it is added a diffusion term to the equation (10). Therefore, the resulting two-pool model for calcium waves takes the form
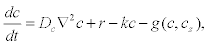 (15)
(15)
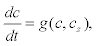 (16)
(16)
Where Dc is the Ca2+ diffusion coefficient in the cytoplasm [25].
Biochemistry and dynamics of protein motors
Kinesins, myosins and dyneis are large families of cytoskeletonbased protein motors that participate in the exocytosis-endocytosis cycles of cells, among many other processes, by transporting organelles and vesicles from the inner regions of the cell towards the periphery [26]. An important case in which these motors play a key role is in the plasmatic membrane resealing of oocytes. Here, as we mentioned in the Introduction section, we will consider the model case of membrane resealing of sea urchin eggs [27,28]. In this case, it has been suggested that protein motors are involved in the docking and delivery of vesicles during exocytosis. Using a confocal microscope, [14] it was observed inhibition of exocytosis in sea urchin eggs injected with kinesin and myosin inhibitors. This observations support the hypothesis that kinesin and myosin motors mediate two sequential transport steps that recruit vesicles to the release sites of Ca2+-regulated exocytosis. From this experiment, it was concluded that kinesin leads the slow phase of exocytosis delivering vesicles along the microtubules from inner regions of the cell, while myosin leads the fast phase, dragging outer vesicles trough filaments of F-actin [14]. It also exists evidence that slow and prolonged release of insulin in β-cells is also a process mediated by protein motors like kinesins and myosins. Finally, it is opportune to mention that theoretical modeling offered clear support to the hypothesis that protein motors are responsible for the translocation of vesicles containing neurotransmitters in the soma of serotonergic neurons [10].
As proteins, enzymes and molecular complexes, the processes developed by protein motors use chemical energy stored into molecules such as ATP or GTP, produced by the mitochondrial system of the cell [1]. This is an interesting issue: protein and molecular motors are strongly coupled to their environments, from which they obtain the “fuel” necessary to perform work during the same process they carry out. That is, molecular machines have not their inner fuel reservoirs. As a consequence of this, their energetics should be described jointly with that of the surrounding medium. In vitro experimental studies determined the dependence of protein motor activity on ATP concentrations with well controlled conditions. This approach has advantages. For instance, it allows for a better analysis of the detailed dynamics of the motors irrespective of the medium, but may hide some aspects of its performance in in vivo conditions, such as the transport of proteins, RNA, vesicles and even organelles [29] that may be related, for instance, to several exocytosis-endocytosis processes [10,27,28,30-32].
Protein motor biochemistry: There are essentially two models that represent the motion of protein motors.
Here, we will focus our attention on the so called handover- hand model, that was first developed to describe the particular problem of intracellular transport via kinesin motion due to ATP hydrolysis [33-36].
The biochemical reaction mechanism modeling the activity of kinesin motors was originally proposed [34] and consists on a sequence of six reactions [37,38]. The first reaction describes the formation of the enzyme-substrate complex MKTαdue to the capture of an ATP molecule (T) by the microtubule (M) kinesin (K) complex MK with the head α of the kinesin attached at position to the microtubule (the head β is free in a retrograde position):
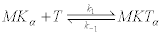 (17)
(17)
In this scheme, the complex MK plays the role of an enzyme that acts over substrate T through a catalyticreaction [34].
The second reaction is controlled by thermal fluctuations that induce conformational changes of the dimer constituting the motor stalk. This produces a secondary enzyme-substrate complex MKT ' α that favors a step forward because corresponds to an advanced position of the β head:
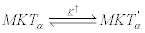 (18)
(18)
In general, this step is influenced by the load f (cargo weight) attached to the kinesin [34].
The next reaction describes the attachment of the free head domain β to the microtubule using an ADP molecule (D) and forming the complex MKTαDβ. This step is considered the slow step of the reaction mechanism and therefore the one determining the overall velocity of the reaction [33]. It is described by
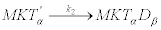 (19)
(19)
This reaction occurs over a high free-energy barrier that cannot be surmounted by thermal fluctuations. After this attachment, two reactions occur that prevent the detachment of the kinesin from the microtubule
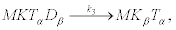 (20)
(20)
And
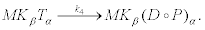 (21)
(21)
The final reaction of the first step corresponds to the hydrolysis of ATP at the active site α of kinesin. This reaction produces an ADP molecule and an inorganic phosphate Pi [35]. Hydrolysis produces a large amount of energy that allows the enzyme to liberate the head α and, in this way, surmount the high freeenergy barrier associated to step (19)
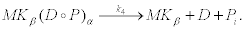 (22)
(22)
After this reaction, the cycle is completed and one recovers an initial state MKβ one step forward from the initial position and with lower free-energy see Equation 17. The number of repetitions of this cycle that the molecular motor is capable to perform determines its processivity. ATP dependence of motor velocities. For our purposes, it is now convenient to consider the dependence of protein motors velocity on the ATP concentration in the surrounding medium. We first recall that motors are activated when cytosolic calcium in its surroundings reaches some critical value  . At this time t0, the motor or the collectivity of motors start their walk along the microtubule carrying a cluster of vesicles towards the cell membrane. The time of activation depends upon motor position in the cell with respect to the origin of the calcium wave.
. At this time t0, the motor or the collectivity of motors start their walk along the microtubule carrying a cluster of vesicles towards the cell membrane. The time of activation depends upon motor position in the cell with respect to the origin of the calcium wave.
Once the motors have been activated, their average velocity determines the rate at which cortical vesicles, both docked to the membrane as far from it, reach an fuse with the cell membrane and are exocyted. In [33] it was suggested that this dependence of the velocity on ATP follows a Michaelis-Menten (MM) kinetics, and therefore the following ATP concentration ([T]) dependence
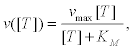 (23)
(23)
Where vmax represents the maximum speed of the motors and KM is the MM constant of the process. We determine both constants from experiments reported in [39] for kinesins in sea urchin eggs. In these experiments, kinesins adhered to a solid substrate move a filament of microtubule for someμm in presence of several ATP concentrations (Figure 5). The velocity of the microtubule is found to be [T]- dependent according to Equation 23. In the following section we will use this dependence to obtain vmax by fitting experimental data with good results.
ADP inhibition and finite time walks. Several experimental studies showed that ADP may inhibit the processivity of protein motors, since kinesin, myosin and dynein heads act as multi-substrate enzymes [31,35,40,41]. More recently, it was probed theoretically in References [37,38], that taking into account the inhibition by ADP in the reaction scheme already discussed, yields a finite number of steps of a single walk of a protein motor. In the case of kinesins, the average number of processive steps predicted was around 60 to 120, in excellent accordance with experimental observations.
Time dependence of protein motors velocity. A consequence of this fact is that the velocity of the protein motors is a function of time. This is clear since each step uses an ATP molecule that, after hydrolysis produces at least one ADP and one Pi molecules. This means: 1) The ATP concentration [T] evolves in time following, in first approximation, a linear relation [37].
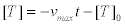 (24)
(24)
where [T]0 is the initial ATP concentration. 2) Considering that the autocatalytic production of [ADP] inhibits the whole reaction scheme, in particular the formation of the MKT enzyme-substrate complex, after many cycles of hydrolysis the ADP concentration can be modeled by a first order kinetics of the form [37,38].
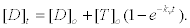 (25)
(25)
After solving the corresponding evolution equations of the chemical kinetics, it was shown that the velocity of a kinesin activated at time t0 can be written in the form [37] (Figure 6).
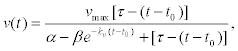 (26)
(26)
Figure 6: Translational velocity of a kinesin motor as a function of time given by Equation 26 with the following values for the constants: values: [T]o = 1mM, [D]o = 0, νmax = 900nms-1, kcat = 113 s-1, kν = 5.600 s-1 and KM† = 2.24μm. Except KM†, all values were taken from reference [35]. Significant values that do not appear explicitly in Eq. (26) like νmax = 11.25μM s-1, [MK]o = 100nM and KM† = 28μM were taken also from reference [35]. Figure taken from Reference [38].
where kv and α are parameters that can be measured in the experiments and the stopping time is given by τ = [T]0/vmax. For the cases when ATP concentration is low, ADP inhibition controls the dynamics of the kinesin, making its velocity strongly dependent on time, as it is shown in figure 6. However, for usual ATP concentrations in living cells, kinesin velocity is practically constant until it stops at a given time that depends on the initial ATP concentrations and the catalytic constants. In rough terms, the stopping time is around τ ~ 70sec, a time that can be correlated to that for the duration of near pools exocytosis [14]. Long time exocytosis may lasts around few hundreds of seconds. Here, it should be stressed that the initial time t0 is determined by the initial position of the molecular motor with respect to position at which the calcium wave initiated, and also by the calcium wave velocity.
Fertilization in sea urchin eggs has been widely studied by biologists of the last century. There is a great amount of experimental evidence describing multiple processes during activation since the contact of the sperm with the jelly: acrosome reaction, calcium wave spreading over the cell, exocytosis of cortical granules and formation of the fertilization envelope. It is known that a cascade of ionic and metabolic changes occur in the sea urchin egg after contact with the sperm [42]. The egg response to the fertilization stimulus is a rapid depolarization of plasma membrane potential establishing the fast block topolyspermy at the time that the eggs demonstrate a brief global contraction within the first 30 sec after fertilization [43].
Simultaneously, another signaling process induces the production of inositol triphosphate (IP3) and diacylglicerol. An increase in (IP3) initiates the release of Ca2+ from intracellular stores and produces a calcium wave, some seconds after fertilization, that travels across the egg form the site of sperm entry to the opposite pole [44,45]. This wave of elevated calcium propagates trough the entire egg. The maximum of concentration occurs in cortical cytoplasm. This wave is preceded by a distinct, short transient spike of calcium in the cortex which correlates with the time of sperm-egg binding [46].
The increase of the intracellular calcium concentration, [Ca2+]i, stimulates in turn a wave of cortical granule exocytosis, resulting in the elevation of the fertilization envelope and formation of the hyaline layer [43]. It has been suggested that this transport of vesicles is carried out by protein motors like kinesins and myosins [14]. Measurements of secreted hyaline, that is, of fused vesicules in the plasma membrane have been reported in [14].
As we have mentioned earlier, kinesin walk is activated and regulated by the presence of ATP and intracellular calcium [14]. In fact, after the local increase of [Ca2+]i, kinesins and myosins, powered by the hydrolysis of ATP, load the cargo and move along microtubules transporting it from the interior of the cell towards the periphery. Using our multiscale model, we show that the calcium wave elevates the [Ca2+]i, allowing activation of kinesins near the cortex of the cell and mobilizing cortical granules to the cell membrane where they fuse and spread their content to the viteline envelope during the process of exocytosis till fertilization envelope is completed.
Calcium waves
During fertilization, after a period of latency which lasts about ~ 7-40 sec, the eggs of seaurchins generate a single ~ 5-min calcium transient that spreads as a wave across the ooplasm [47]. In Lytechinus, induced calcium wave is directly preceded by an influx of calcium leading to a cortical flash and is followed by a few post-fertilization calcium transients [46]. This wave spreads throughout the entire egg with a spherical wave front and velocity between 5-10 μm/s [48]. It is known that external calcium is needed at the onset of sea urchin natural fertilization [1]. This calcium is available from the sea water in the moment of sperm entry during the acrosome reaction [49]. Unfertilized sea urchin eggs can release internal calcium stores via IP3 or non- IP3-mediated mechanisms [45] (Figure 7). Following insemination, a calcium wave occurs in the presence of inhibitors against inositol triphosphate receptors (IP3R s) or ryanodine receptors (RyR’s) but not when both inhibitor types are used, suggesting that the two receptors may redundantly participate during fertilization [50]. Therefore, we will assume that the calcium dynamics within the fertilized egg can be modeled with the two pool extended model. We will suppose that the endoplasmic reticulum (ER) represent the only internal store of calcium with the release modulated by both IP3 and Ca2+. In addition, we will suppose that the network of the ER spreads approximately inside the entire cell [51]. If c and cs represent concentrations of cytosolic and stored Ca2+, respectively, and we assume that only the first one is free to diffuse at rate Dc, then the dynamics of calcium is dictated by Equations 15 and 16.
We solved Equations 15 and 16 using a Finite Element Method. As a domain, we used a circle of radius ~ 50 microns [48] with a closed border except at the point marked by the arrow in figure 7, where an initial concentration slightly higher than the equilibrium concentrations simulates the entrance of external calcium due to the acrosomic reaction. For the equations 15, 16, we fix typical values of the chemical parameters and adjust the coefficients Dc and rin such a way that: 1) cytosolic calcium spreads as a single wave over the cell, as observed in experiments; 2) the wave spreads with a circular wave front; and 3) the velocity were in accordance with the experiments reported in References [50,51], see also References [43,44,52]. We obtained that the two-pool model reproduces remarkably well the spatio-temporal evolution of the calcium wave in the oopplasm. Our results are represented in the left panel of figure 8 where the time evolution of the calcium wave is compared with the results observed in Reference [50], right panel. In this figure 8, at time t = 0, the small red semicircle indicates the point at which takes place the initial local elevation of calcium concentration, that is, where the acrosomic reaction takes places. Theblue color indicates the low basal calcium concentration inside the oocyte before stimulation. Front velocity and shape are very similar to the experimental ones. This allows to reproduce the formation of the vitaline envelope because the activation of the motors occurs at times very similar to the experimental ones. The model does not represents well the time scale for the reduction of calcium concentration which in the experiments may last few minutes.
Figure 8: The left panel shows the results from our simulation of a calcium wave using the Finite Element method. Parameters in equations (15) and (16) are given by r = 0.0075μM, V1 = 0.45μ M s-1, k1 = 0.9μM, V2 = 2275μMs-1, k2 = 2μM, k3 = 0.9μM, k = 0.04s-1, kf = 0.005s-1, Dc = 50μms-2, l = 2, m = 2 and p = 4. Cytosolic and stored calcium are set up at their equilibrium values c = 0.1666 M and cr = 2.92M in almost all the domain, except by a perturbation in the first one of value 1.3μM in the upper left part of the cell. We have used zero flux boundary conditions. Images are taken every 4 sec. Red and blue correspond to maximum and minimum of cytosolic calcium concentration respectively. The right panel correspond was taken from Reference [51] and shows an experimentally observed calcium wave within a sea urchin egg.
Protein motors activation and dynamics
Once having the calcium dynamics, then we proceeded to study the dynamics of protein motors based on the model discussed in SECTION IIC SIGNIFIES. One hypothesis of this model is that the speed has a Michaelis-Menten dynamics type. In the case of kinesin present in the sea urchin egg, this assumption can be corroborated through the experiments reported in References [39]. In the cited work, a partially purified kinesin is adsorbed to a glass coverslip and mixed with microtubules and ATP. The translocating activity of kinesin to microtubules is observed by contrast microscopy atdifferent concentrations of ATP. Experimental data have been fitted with Equation 23 by least squares, corroborating that velocity follows a Michaelis-Menten dynamics. This result gives the maximum velocity entering Equation 26 for the speed of kinesin as a function of time. In figure 9, we show several possible velocity profiles varying two different parameters (k, and vmax). While vmax clearly controls the maximum speed reached by a kinesin, kv indicates how smoothly the kinesin started his walk. In these fittings, we have used that average kinesin walk takes about 70 seconds, in accordance with experimental results. The molecular motor is rapidly activated after calcium increase and starts carrying the transported vesicles to the plasmatic membrane of the oocyte.
It is convenient to stress that the time at which a motor starts its walk depends on its distance from the point of fertilization and to the cell cortex. Vesicles near the entry point of the sperm come quickly to the plasmatic membrane. Those initially located far away from the stimulation point have a larger latency for the initialization time ti that depends on the calcium wave velocity and shape. The important result represented in figure 9 is that, given the ATP ooplasm conditions, the velocity of the protein motors is almost constant within the duration of the exocytosis. Note from figure 6, that for large ADP concentrations present, the velocity profile as a complicated time dependence, see for instance, thedashed-dotted line.
Figure 9: Possible velocity profiles of molecular motor as a function of time. We fix the values of α = 4.8s and β= 4.7s in equation 26. The values of kv are 5.6x103s-1 for orange and red lines, and 8.9x10-1 s-1 for green and blue. Note that a smaller value of this parameter softens engine acceleration at the beginning of its walk. The values of vmax are 5.25, 3.25, 1.5 and 0.44 micrometers per second from top to bottom.
Directed diffusion and cumulative exocytosis. Finally, we quantify the results of cumulative exocytosis reported in [14] by linking the previous theoretical results through the diffusion model. In these experiments, the number of vesicles that are secreted is counted as a function of time over the plasmatic membrane of the egg using confocal microscopy. Experiments show that decreasing the externalcalcium causes a slower rate of exocytosis. These results can be understood, at least qualitatively, usingthe diffusion model discussed in what did section II A SIGNIFIES. In view of the results already discussed for the time dependence of motor velocity, we may simplify the numerical resolution of the diffusion equation by assuming, in first approximation, that kinesin moves with a constant velocity. Then we solve numerically equation 2 and reproduced the experimental data on cumulative exocytosis by adjusting the parameters (diffusion coefficient, friction coefficient, frequency, initial position of the vesicles and motor velocity). As it is shown by the lines in figure 1, the fits of the cumulative exocytosis with this model is excellent, and gives many important information on vesicle distribution, motor speeds and the viscoelastic properties of the cell that otherwise remain hidden. This information is contained in table 1, where the values of the diffusion coefficient, the average protein motor velocities, the initial distance between the clusters of vesicles with respect to the plasmatic membrane and the number of vesicles per cluster are reported. These values correlate well with those obtained in other works [10], although in the present case the average velocity is much higher, fact possibly related with the biological nature ofthe response. The number of vesicles per cluster is only indicative and approximate, since no direct comparisonwith the ultrastructure of the cell allows to compare these values. In addition, fluorescence measurements should be normalized to a given region and the efficiency of vesicle fusion with the membrane was assumed equal to one.
| color | Dν(μm2s-1) | ν(μms-1) | d(μm) | n |
|---|---|---|---|---|
| Green | 0.6 | 10. | 5 | 47 |
| orange | 0.7 | 0.2 | 8 | 76 |
| blue | 0.6 | 0.05 | 8 | 27 |
Table 1: Parameters of the model for the three profiles of Figure I. See text for details.
The fits of the calcium wave using the two-pool model (with the inclusion of the diffusive term) correctly reproduce the profile and speed of the calcium wave in itsinitial propagation through oocyte. Not with standing, forthe recovery period in which calcium concentration decreases to its basal value we have found (of about 60 seconds) is well below that found in fluorescence experiments of about 7 minutes [44]. This can be improved in our model considering the continuous exchange of calcium with the outside and not only at the time of the initial application. Furthermore, in our present work, the stores of calcium inside the cell are distributed homogeneously within the cell, and therefore could no replicate the rapid increase of calcium near the cell membrane at the moment of fertilization [46]. We thought this can bedue to the greater presence of calcium stored in outer regions of the egg. However, for qualitative purposes, the occurrence of calcium waves founded with the two pool model helps to understand the exchange mechanism which produces calcium waves inside the egg.
We have satisfactory found that engine speed obeys a Michaelis- Menten dynamic, corroborating that a kinesin can reach a speed of up 5.25μms-1in in vitro experiments with high concentrations of ATP. However, the models presented in this work allow us to think that this velocity may be much lower in the fertilized sea urchin eggs, where the engine speed when carrying vesicles is severely limited not only by the availability of intracellularATP [38], but also by the conditions of friction or drag of the intracellular environment where it moves [10,13]. It is therefore not surprising that in our fittings of cumulative exocytosis, the effective velocity we found on our adjustments (between 1 and 0.05 μms-1) is substantially lower than that of in vitro experiments. For the purposes of this model, we assumed a constant motor speed, however, more accurate results may be obtained following the time dependence reported in [38]. This may allowone to understand that this is only an approximation for intracellular processes with a time scale considered comparably high to the acceleration and deceleration of kinesin. However, these speed changes can be crucial in terms of energy to understand the processivity and stop of these motor proteins.
The diffusion model and drag of the transported vesicles within a cell proposed by Santamaría-Hólekin [10] proves to be extremely successful in quantifying cumulative exocytosis in eggs of sea urchins. However, when coupled with the calcium wave patterns, processivity of molecular motors, applicability of this model to this biological system could be expanded to explain and quantify the formation vitaline envelope emerging into the egg to prevent polyspermy. This is due to the fact that the model perfectly differentiate the start and coupling of each process: when the fertilization process starts, it emerges a wave of calcium whose concentration is known at each position as a function of time [25]; when the calcium concentration reaches locally a critical value at time ti, a molecular motor begins its walk dragging outward a vesicle [38]; the rate and the number of vesicles arriving at each position can be determined by the conditions of diffusion and drag of the medium [10]. Thus, excepting the numerical complexity of coupling all the required equations, the above model would allow us in the future to quantify the spatio-temporal distribution of secreted vesicles and understand the formation of the envelope.
The multi-scale models are very useful when trying to describe processes whose causes are described in different spatio-temporal scales, fact which occurs in most biological processes. In this paper, we have revisited the description and modeling of three particular physicochemical mechanisms that are essential in secretion processes: a) formation of calcium waves, b) the dynamics of molecular motors based on its biochemistry, and 3) directed diffusion of vesicles within a fertilized egg.
Within this analysis and with the help of previously Published Date: results in literature, it was found that the extended two-pool model can be used to understand the propagation of calcium waves in the ooplasm of sea urchin eggs. Furthermore, the approach we followed in our work has the advantage of allowing the integration of specific information of other cell types where these waves occur, for instance: geometry, exchange flows with the extracellular medium, location of internal pools and intensity of initial application. We also reviewed and used a modelfor the processivity of protein motors which is based on their biochemistry. This model yields the time dependent velocity profiles for the kinesin, protein which plays a key role in the translocation of clusters of vesicles in many cell types. For this, we reviewed and solved a simple diffusion model for vesicle transport that integrates various factors affecting the movement of vesicles before fusing with the cell membrane, namely diffusion and drag forces due to the activity of protein motors. By solving this three component model, we have successfully quantified cumulative exocytosis previously reported in literature.
More importantly, in this paper we have described how these three schemes can be integrated to quantify with accuracy the formation of the viteline envelope. For this, in addition to the description of each model, we proposed the relationships between each of them, relationships which are essential to understand this complex process. Thus, this work establishes a theoretical foundation useful for the understanding and analysis of secretion processes, whose difficulty now is merely based on thenumerical resolution of mathematical equations.
In future work, we pretend to propose a more detailed quantitative model which will consider aspects related to the kinetics of docking and priming of the vesicles in the porosomes [5,6], as well as the detailed mechanical description of swelling of the vesicles and the expulsion of its content.
We acknowledge N. J. López-Alamilla for useful discussions. ALD acknowledges Contact for financial support under fellowship 221505.