The CFD grow to be instrument for developing, sustaining, optimizing, innovating, verifying and, particularly here, for validating steps. The CFD has become a widely used tool for aerodynamic applications. On Aerodynamics, the four main forces which act on the aircraft during the flight are Lift, Drag, Thrust and Weight. Drag is one of the most critical phenomena amongst all and is the opposing force of aircraft’s forward motion, [1, 2]. A class of body exists, however for which a wing profile is not symmetrical (or when there is a nonzero angle of incidence); a velocity difference is upheld between upper and lower surfaces. This creates a pressure difference and a circulation around the wing: lift is generated, [3].

Airfoil is famous aerodynamic shape that used in aeronautical applications. When the aerofoil is in motion through air, the air is passing above and below the wing. The wing’s upper surface is shaped so the air velocity increases. The air pressure above the wing decreases. The wing’s lower surface is shaped so the air velocity decreases. The air pressure above the wing increases. Lift of a wing is produced by high pressure on the lower surface and low pressure on the upper surface. And when the force of gravity is lower than the force of lift, the airplane is able to fly [4-6].

From Figure 1, at the front of the airfoil, the leading edge is the point has the maximum curvature. At the rear of the airfoil, the trailing edge is defined the point of maximum curvature. A straight line connecting the leading and trailing edges points of the airfoil is the chord line. AOA is the angle between the direction of air velocity and a chord line on the wing [7]. AOA increases when the nose of the wing pitches up, and lift increases. Drag increases also, but not the same as lift. The drag force, lift force, pitching moment equations are shown in equations (1), (2), (3).

D= ½ ρ ×V₂ × S× C_D       (1)

L = ½ ρ ×V₂ × S× C_L      (2)

M = ½ ρ ×V₂ × S× C× C_M      (3)

The investigation of the 2D subsonic flow over a NACA 0012 airfoil at different AOA and running at a Reynolds number of 3000000 is considered by [8]. In this project, the steps of computational solution are consisting of three stages as shown in Figure 2. The project starts from preprocessing step of geometry design and grid generation. The model geometry and the grid are generated by GAMBIT® 2.3.16. The second step was solving equation of motion by FLUENT solver using Finite Volume Approach. Finally is the post-processing step where the aerodynamics properties of NACA653218airfoil. Then the drag, lift, pressure contours, pitching moment coefficient, path lines and velocity contours around aerofoil at all AOA are determined by CFD package.

The air flow is modeled as 2-D compressible viscous flow. Thus the governing equations are the continuity equation together with x- y and z governing equations for a compressible flow. Turbulence is modeled by the Spalart-Allmaras model. The complete system of equations is presented here in differential form, FLUENT® Documentation [9] and [10]. The governing equations in this model are:

Figure 1: Basic properties of an airfoil.

Figure 2: Three steps of present CFD model.

Continuity equation in vector form:

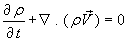
Momentum equation in vector form:

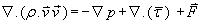
Energy Conservation Equation:

The energy equation is applied on the control volume that is primarily derived from the first law of thermodynamics. The energy equation may be written in the differential form as:

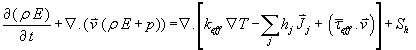
Numerical model of NACA653218 airfoil

Figure 3, the numerical model of NACA653218airfoil is shown below:

Boundary conditions: The flow field, temperature, pressure and Mach number in the numerical model of NACA653218airfoil considered are solved by FLUENT®, with the following boundary conditions:

Pressure far field: At Pressure far field boundary, Reynolds number (as shown in Figure 1) was Re=3x106, same with the reliable experimental numbers from [11,12], to validate the present CFD simulation. The free stream temperature is 288.2 K, which is the same as the environmental temperature. The density of the air at the given temperature is ρ=1.225kg/m³, the pressure is 101325 Pa and the viscosity is μ=1.7894×10^-5 kg/m s. A segregated, implicit solver is utilized (ANSYS FLUENT® processor) calculation were done for varies angles of attack range from -5 to 16°. The airfoil shape, boundary conditions and meshes are created in GAMBIT® 2.3.16 as a pre-processor.

NACA653218airfoil: The NACA65₃218airfoil is considered adiabatic and no slide wall, as shown in Figure 3.

Drawing of NACA65₃218airfoil: According to airfoil database [13], scatter drawing of an aerofoil in this problem was a 6-digit NACA series, NACA653218airfoil. The airfoil is drawn using GAMBIT® 2.3.16, as shown in Figure 4.

Grids near the airfoil wall boundary must be dense enough and computed fields must be large enough to satisfy far field boundary conditions to obtain accurate aerodynamics properties such as drag, lift, and pitching moment on airfoil. However, extreme grids will cost too much computing resources and increase computing time. Thus, the compromise is that grids far from the airfoil wall boundary are scattered and grids near the airfoil wall boundary are intense. Figure 3, is shown Computed fields where right part are two rectangles, where AB=ED=GC=20c, and AG=GE=12.5c. Left part is a half circle with a center at G, and a radius of 12.5c.

It is meshed each of 3 faces individually to get our final mesh. Figure 5(a), shows all grids in computed fields. By performing the command “Grid Check” in FLUENT, it is known that total number of grids is 100000 quadrilateral cells, the volume of the smallest grid 4.1224x10-10 m³, and the volume of the largest grid 9.3985x10^-1 m³. Figure 5(b), shows the grids surrounding the airfoil.

Figure 3: NACA65₃218 airfoil numerical model.

Figure 4: NACA65₃218 aerofoil shape.

Figure 5: Grid computed flow field surrounding the clean NACA65_3218 airfoil.

Solver

FLUENT® package is used to calculate the flow field and properties through the different configurations. Simulations as Velocity contours, Pressure contours, drag and lift coefficients values by the same package.

Convergence criterion

Continuity equation, linear momentum equations and turbulence model Spalart- Allmaras equations are calculated for the mesh control volumes to a residual of 10^-3, while energy equation is calculated to a residual of 10^-6.

Grid dependency check

It should be to investigate the grid size effect on the solution results for the first step in performing a CFD simulation. Generally, a numerical solution to be further accurate as more cells are used, but using added cells also increases the essential computational time and computer memory. The appropriate number of cells is determined by increasing the number of cells until the grid is satisfactorily fine so that further refinement does not vary the outcomes. To check the independency of the outcomes to cell number, seven types of grids are produced. The results of these seven grids are seen in Table 1, at stall AOA (15°).

Figure 6 explains the effect of number of mesh cells in aerodynamic lift coefficient at stall AOA (15°).

Figure 7 explains the effect of number of mesh cells in aerodynamic drag coefficient at stall AOA (15°).

Figure 8 explains the effect of number of mesh cells in aerodynamic moment coefficient of at stall AOA (15°).

In order to save time when running the computations, the grid with the smallest number of cells displaying an independent solution should be used for the calculations. This is seen to be the case for a grid with around 100000 cells.

Verification of numerical model

A similar Numerical Model NACA653218airfoil of the same previously-mentioned grid size and type was developed, for verifying numerical model with experiment and numerical models measurements. The NACA65₃218airfoil model was used to verify the work done by [11-13]. To apply the same boundary conditions at pressure far field, temperatures are 288.2K, velocities are 43 m/s, pressure is 101325 Pa. The density of the air at the given temperature is ρ=1.225kg/m³, the viscosity is μ=1.7894×10-5 kg/m s at Re=3x106. The NACA65₃218airfoil is considered zero heat flux wall and no slide wall. Compare the outcomes of the numerical model by standard k – ε model, RNG k – ε model, the standard model k–ω model and Spalart-Allmaras turbulence model to those of the numerical and experimental models measurements. The results show good agreement of lift, drag and moment coefficients with the corresponding values in the experimental and numerical models measurements. Figure 9; see the coefficient of lift (C_L) with AOA from -4 degree to stall angle of attack 16 degree of numerical models and experimental studies, plotted on the same axes and scale for comparison. By Spalart-Allmaras, it is found maximum error model about 12% but for standard k – ε model, RNG k – ε model, the standard model k–ω model it is found maximum error increase from Spalart-Allmaras model maximum error and reach in k–ω model about 60%.

Figure 6: Aerodynamic lift coefficient at stall AOA against number of mesh cells.

Figure 7: Aerodynamic drag coefficient at stall AOA against number of mesh cells.

Figure 8: Aerodynamic moment coefficient at stall AOA against number of mesh cells.

Figure 9: Lift coefficient values comparison between present numerical results and experimental results.

Figure 10: Drag coefficient values comparison between present numerical results and experimental results.

Figure 10; see the coefficient of drag (CD) with AOA from -4° to stall angle of attack 16° of numerical models and experimental studies, plotted on the same axes and scale for comparison. By Spalart-Allmaras model, it is found maximum error about 25% but for standard k – ε model, RNG k – ε model, the standard model k–ω models, it is found maximum error increase from Spalart-Allmaras model maximum error and reach in k–ω model about 300%.

Figure 11 see the coefficient of pitching moment (C_m) with AOA from -4° to stall AOA 16° of numerical models and experimental studies, plotted on the same axes and scale for comparison. By Spalart-Allmaras model , it is found maximum error is about 30% but for standard k – ε model, RNG k – ε model, the standard model k–ω models, it is found maximum error increase from Spalart-Allmaras model maximum error and reach in k–ω model about 500%. It concluded the Spalart- Allmaras model more Accurate than standard k – ε model, RNG k – ε model, the standard model k–ω models.

Figure 12 show the velocity contours explain the flow development from α= -4° to α=16°. The range values of all figures shows maximum value of velocity about 130 m/s obtained for α=16°. At α= -4° it is shown that the low velocity area value around leading edge is small, and it starts to disappear with increasing the AOA then start building up from α=8° raises steadily up to approximately α=16°on pressure side of aerofoil. From around =10° the separation is clearly seen and reattaches to the suction side at trailing edge of the airfoil and the separation area raises until it arrive at about 50% of the suction side of the airfoil at α=16°.

Figure 11: Numerical results of Cm in comparison to corresponding experimental results.

Figure 12: Velocity contours around the leading edge for clean airfoil case. 1st row: α =-4 °(left) and α =-2° (right), 2nd row: α =2° (left) and α =4° (right), 3rd row: α =8° (left) and α =10° (right), 4th row: α =14° (left) and α =16° (right). Values are in m/s at Re=3*10⁶.

Figure 13: Streamlines for clean airfoil case (a) Streamlines for clean airfoil case at α=2° and (b) Streamlines for clean airfoil case at α=16◦. Values are in kg/s. Re=3*10⁶.

The reason for the streamline unit kg/s not kg/m.s is the 2D geometry. The missing m in the denominator denotes per unit depth. It is evident from Figure 13(a) that the flow at α=2° to is rather smooth and well attached to the surface of the airfoil. It is evident from Figure 13(b) that the flow at α=16° a separation bubble starts to form at the trailing edge and moving upstream for bigger angles of attack.

• By using CFD to calculate performance of numerical model NACA65₃218airfoil, huge amount of time and money can be saved before testing the wing in the wind tunnel. Calculations show that trends of numerically-simulated curves are in excellent agreement with trends of experimentally-obtained ones.

• The Spalart-Allmaras turbulence model was found to be more Accurate than standard k – ε model, RNG k – ε model, the standard model k–ω models.

• Lift coefficient increases with increases AOA. After stall AOA about 16 degree, Lift coefficient decreases.

• Drag coefficient increases with increases AOA.

List of symbols

C Chord length

C_L Lift coefficient

C_D Drag coefficient

CM Moment coefficient

D Drag force

E Total energy of a fluid

P Particle constant

h Enthalpy

M Mach Number, Pitching moment

S Reference area

P Pressure value

Re Reynolds number, Re = ρ U Lc / μ

t Time

T Temperature

u Instantaneous x direction velocity

v Instantaneous y direction velocity

w Instantaneous z direction velocity

x, y, z Cartesian coordinate components

Greek Letters

α Angle of attack

ε Turbulence dissipation rate

μ Dynamic viscosity

μt Turbulent viscosity

ρ Density

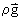Gravity body forces

List of Abbreviations

AOA Angle of attack

CFD Computational Fluid Dynamics.