Journal of Aeronautics & Aerospace Engineering
Open Access

Numerical Simulation of the Influence of Different Ice Shapes on the Unsteady Oscillation of Airfoils

Zhixin Sun^*, Hantao Liu, Haiqiao Li and Jing Liu ^*Correspondence: Zhixin Sun, Department of Energy and Power Engineering, North University of China, Taiyuan, China, Email:

Author info »

Introduction

When aircraft operate under icing meteorological conditions, ice accretion on their surfaces poses a significant threat to flight safety. A notable incident occurred on October 31, 1994, involving an American Eagle Airlines ATR-72 aircraft flying from Indianapolis, Indiana, to Chicago. The aircraft lost control and crashed into a farm field in Roselawn, resulting in the tragic death of all 68 occupants. The National Transportation Safety Board (NTSB) investigated the accident and identified several factors contributing to the disaster, notably design flaws under icing conditions and inadequate pilot awareness of icing phenomena [1]. In 2006, a similar unfortunate incident occurred involving a Chinese airborne early warning aircraft, highlighting the persistent research focus on aircraft icing and its associated challenges since the June 3rd, 2006 air disaster. Prediction and determination of ice types are critical in addressing aircraft icing issues. While extensive research on numerical simulations of static airfoil icing exists both domestically and internationally, the dynamic oscillation of wings during actual flight conditions persists. These oscillations influence ice formation and directly affect wing profile modifications, thereby impacting aerodynamic characteristics. Therefore, understanding the effects of different ice types on the aerodynamic characteristics of aircraft wings during non-steady oscillations is currently an important research direction [2]. This research aims to accurately simulate ice formation under complex conditions, thereby facilitating improved prediction and determination of ice types.

Determination of ice types

In clouds, water droplets and ice crystals often exhibit various types, with the arrangement of water molecules determining the distinct shapes of ice crystals [3]. Due to varying specific conditions during aircraft icing, different types of icing formations can occur. Through extensive observations, aircraft icing is categorized into four types based on their mixed ice structure, shape, and impact on flight: Rime ice, glaze ice, mixed ice, and frost [4].

Rime ice: Rime ice, also known as "opaque ice" or "milky white ice," refers to ice formed when supercooled water droplets come into contact with the aircraft surface and freeze before spreading, typically occurring under relatively low air temperatures (below -10 °C), small water droplet sizes, low liquid water content, and slow flight speeds [5]. Figure 1 illustrates rime ice formations observed under icing wind tunnel conditions, showing rime ice formations that closely adhere to the shape of the wing leading edge, often presenting as relatively regular wedge-shaped forms, also referred to as "wedge ice."

Figure 1: Rime ice formation observed under icing wind tunnel conditions.

Glaze ice: Glaze ice is a transparent type of ice and considered one of the more hazardous forms of icing. Figure 2 shows the glaze ice formation under icing wind tunnel conditions [6]. Glaze ice typically forms under conditions of relatively higher air temperatures, larger water droplet sizes, higher liquid water content, and faster flight speeds.

Figure 2: Glaze ice formation observed under icing wind tunnel conditions.

Mixed ice: Rime ice and glaze ice are often idealized descriptions. In reality, mixed ice is frequently observed, exhibiting characteristics of both rime and glaze ice. Specifically, the leading edge stagnation point area is transparent glaze ice, while the trailing part is surrounded by rime ice feathers. Figure 3 illustrates experimental conditions in an icing wind tunnel showing images and forms of mixed ice [7]. Mixed ice can form in cloud layers between -10 °C- 20 °C, especially when the cloud contains both supercooled water droplets and ice crystals. Due to its rough surface and irregular shape, coupled with a solid freeze on the surface, mixed ice poses a hazard to flight comparable to glaze ice [8].

Figure 3: Experimental conditions in an icing wind tunnel showing forms of mixed ice.

Frost ice: Frost ice, also known as hoar frost, is not formed by freezing of supercooled water droplets. It refers to a type of aircraft icing where water vapor in the air directly freezes on the aircraft surface when its temperature is below the ice point corresponding to the vapor pressure of surrounding air [9].

Aircraft icing typically occurs between the ice point and -40 °C, with the highest probability and severity of icing between -4 °C-20 °C. When temperatures drop below -20 °C, the likelihood of aircraft icing decreases due to lower concentrations of supercooled water droplets in the atmosphere. Aircraft icing occurs within altitudes ranging from 0 km to 7 km [10]. Above 7 km, the concentration of supercooled water droplets in clouds is minimal, resulting in negligible icing events. Aircraft icing generally occurs at speeds below 600 km/h; at speeds greater than 600 km/h, aerodynamic heating raises surface temperatures above 0 °C, thereby reducing the likelihood of icing.

To investigate the influence of different types of ice on the aerodynamic characteristics of aircraft wings, this study selected two common ice formations: Glaze ice and rime ice, corresponding to temperatures of -7.4 °C-20 °C, respectively, as shown in Figures 4a and 4b. These temperatures are representative and hold significant research value. The experiments were conducted with water droplet Mean Volume Diameter (MVD) of 20 μm and liquid water content of 1 g/m³. Using Computational Fluid Dynamics (CFD) with structured overlapping grid techniques, the study examined the unsteady aerodynamic characteristics and lift hysteresis variations of oscillating aircraft wing airfoils at different angles. User-Defined Functions (UDF) were employed to design controlled pitching oscillations of the iced wing and surrounding dynamic grid regions. This enabled the wing to oscillate sinusoidally as expected, with amplitudes and equilibrium angles meeting predefined criteria. Flow field information was interpolated at each time step using overlapping grid interpolation, ensuring controlled precision and efficiency in obtaining aerodynamic parameters throughout different oscillation cycles.

Figure 4: Schematic diagram of ice structures: (a) T=-7.4 ℃ (Glaze ice), (b) T=-20 ℃ (Rime ice).

Mesh generation

The use of overset grid techniques to solve pitching motion problems is an efficient computational method. In numerical simulations involving motion, the overset grid system does not require re-meshing. The grids for each object are independently generated in the initial stage, resulting in rapid grid generation with high quality. The data structure is simple, and the density of each grid can be controlled. The transition between the overlapped moving and background grids is smooth, allowing for effective transfer of flow field information through interpolation at the overlapping boundaries under different conditions. As the object moves, interpolation is performed at the boundaries of the moving grid region. The overset grid technique reduces grid deformation, prevents grid distortion, and ensures efficient hole cutting and high interpolation accuracy during computation [11].

For the study of airfoil pitching oscillations, the overset grid consists of two independent grid systems: The background structured grid region and the structured moving grid region that performs pitching motion around the airfoil's center of gravity. The moving grid region is enveloped by the background grid. The computational domain size of the background grid is more than 10 times the chord length of the airfoil. The moving grid region can complete pitching oscillation around the airfoil reference point. In areas with significant changes in flow field parameters, the grid is refined, while in areas with smaller parameter variations, the grid is coarser. This approach effectively captures flow field details while saving computational resources [12]. As shown in Figure 5, the mesh division near the wall ensures that the first-layer grid y+ ≤1, with the total number of structured grid elements being approximately 200,000.

Figure 5: Schematic diagram of grid division.

Methodology

The unsteady pitching oscillation of the airfoil, given a specified amplitude and equilibrium angle of attack, is controlled by timebased sine or cosine equations. Reasonable time steps are chosen to ensure the consistent variation of the airfoil's attitude at each time step. This study focuses on the NACA 0012 airfoil, which pitches around a point located at 25% of its chord length from the leading edge. The pitching oscillation motion is described by the following equation:

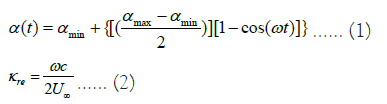
Where α_max and α_min represent the maximum and minimum angles of attack during the pitching oscillation, respectively, ω is the angular velocity of the pitching oscillation, and κ_reand U_∞ represent the reduced frequency, chord length of the airfoil, and free stream velocity, respectively. By defining the dynamic mesh region, the airfoil oscillates from the minimum angle of attack, through the equilibrium angle of attack, to the maximum angle of attack, and then returns to the starting position.

Considering the complexity of the unsteady flow field in dynamic stall of the airfoil, the Reynolds-averaged Navier-Stokes (N-S) equations are used for the analysis of the dynamic aerodynamic characteristics of the airfoil [4]. The N-S equations include the three main conservation laws: Mass conservation, momentum conservation, and energy conservation. In Cartesian coordinates, the integral form of the three main fluid control equations can be expressed as follows:

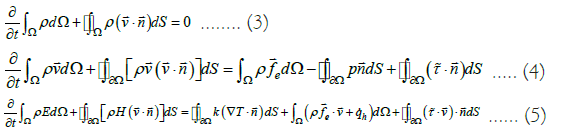
Given the complex flow field phenomena during the dynamic stall process of the oscillating airfoil, including high adverse pressure gradients and turbulence levels, it is necessary to use a turbulence model that can accurately simulate separated and shear flows [5]. The k −ω SST turbulence model, proposed by Maresca et al. combines the advantages of the k −ω model in simulating nearwall turbulent regions and the k −ε model in simulating farwall turbulent regions [13]. This model has good capabilities for simulating separated flows and adverse pressure gradient flows, and it can be applied to the unsteady boundary layer flow, separation, vortex generation, shedding process, and transition at different oscillating angles of attack. Therefore, the k −ω SST model is selected for this study. The turbulence kinetic energy transport equation and the specific dissipation rate equation of the model are as follows:

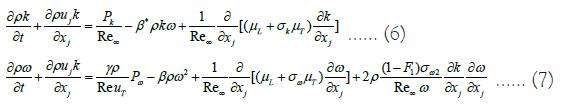
In this context, the turbulent kinetic energy production term k P is modeled using the Boussinesq approximation. The expressions for the turbulent kinetic energy production term P_k and the specific dissipation rate production term P_ω are given as follows:

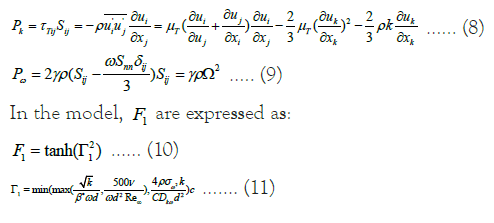
The term 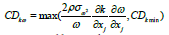represents the cross-diffusion in the model, typically taken as 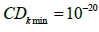denotes the distance normal to the wall from the computational point.

Result and Discussion

Aircraft icing directly alters the aerodynamic shape of the aircraft, thereby affecting its aerodynamic performance. Figure 6 compares the lift coefficient of two different ice shapes with the clean wing model. The green circles represent the clean wing, the blue diamonds represent the wing with glaze ice, and the red triangles represent the wing with rime ice. From Figure 6, it can be observed that the lift coefficient of the wing during un-iced conditions exhibits a well-defined linear closed-loop behavior during the entire upstroke phase of the wing's non-steady oscillation. Compared to the clean wing, the lift coefficient changes similarly for the wing with rime ice during the entire upstroke of the oscillation, showing only a slight increase at low angles of attack. This behavior is largely influenced by the regular shape of rime ice, as depicted in Figure 4b, which effectively increases the chord length of the wing to some extent. When rime ice adheres to the leading edge of the wing, it enhances the aerodynamic surface area of the lower wing surface. On the other hand, the lift coefficient of the wing with glaze ice remains consistently lower than that of the clean wing throughout the entire upstroke phase, with an average decrease of 7%. The maximum difference occurs at α = 6.5° . Throughout the entire downstroke phase of the wing's non-steady oscillation, the lift coefficient of the wing with rime ice is significantly lower than that of the clean wing, averaging a decrease of 7.5%. The maximum difference occurs at α = 7° . Meanwhile, the lift coefficient of the wing with glaze ice varies considerably within the range of -3.5° to 8.5° of attack angle, consistently lower than that of the clean wing with an average decrease of 12%. The maximum difference occurs at α = 4° , accounting for 10% of the total difference. This behavior is largely attributed to the distinct angular and groove characteristics inherent in glaze ice formations.

Figure 6: Lift coefficient comparison plot. Note: T=-7.4 °C (Glaze ice); T=-20 °C (Rime ice); 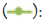Clean airfoil.

Figure 7 depicts the drag coefficient comparison among two different ice shapes and a clean wing profile. From Figure 7, it is evident that both the wing profiles with glaze ice and rime ice exhibit increased drag coefficients during non-steady oscillatory motion. Due to the larger size of supercooled water droplets frozen in glaze ice, its surface is smooth, transparent, and densely structured, which results in stronger adhesion to the components. Consequently, the drag coefficient for the wing profile with glaze ice shows a significantly more pronounced increase, averaging 2.1 times higher overall. In contrast, rime ice, characterized by poor transparency, loose structure, susceptibility to shedding, and rough surface, leads to a 1.5-fold increase in drag coefficient compared to the clean wing profile. Both ice shapes have substantial effects on the aircraft's drag.

Figure 7: Drag coefficient comparison plot.Note: T=-7.4 °C (Glaze ice); T=-20 °C (Rime ice); 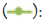Clean airfoil.

Figure 8 illustrates the moment coefficient comparison among two different ice shapes and the clean wing. From Figure 8, it is evident that the moment coefficient of the clean wing shows a regular and well-defined closed-loop pattern during non-steady oscillations. Both ice shapes exhibit an overall decreasing trend in moment coefficient during the upward oscillation phase. At an amplitude of 10°, the moment coefficients of both ice shapes are lower than that of the clean wing. Conversely, at an amplitude of -10°, the moment coefficients of both ice shapes exceed that of the clean wing. During the downward phase, the moment coefficient of the clear ice oscillates irregularly due to its irregular shape, which can have a certain negative impact on aircraft flight.

Figure 8: Moment coefficient comparison plot. Note: T=-7.4 °C (Glaze ice); T=-20 °C (Rime ice); Clean airfoil.

Figures 9a-9c presents the pressure coefficient contour plots comparing two different ice accretion shapes with a clean wing model at various oscillation angles. Figures 9a-9c correspond to oscillation angles of 3.5°, 13.5°, and-6.5°, respectively. From Figure 9a, it can be observed that at an oscillation angle of α = 3.5° , the pressure coefficient near the leading edge of the wing accreted with clear ice is relatively large and concentrated, similar to the pressure distribution of the clean wing model. This suggests that the influence of clear ice accretion on the pressure coefficient is minimal at low angles of attack. In contrast, the leading-edge pressure coefficient distribution of the wing accreted with glaze ice exhibits significant differences, with scattered and higher values. On the upper surface of the wing accreted with glaze ice, compared to the clean wing model, the pressure coefficient is increased and the distribution range is broader. This phenomenon is associated with the regular surface of glaze ice, which to some extent increases the chord length of the wing, thereby altering its aerodynamic performance. From Figure 9b, it can be observed that as the oscillation angle increases to α =13.5° , the pressure coefficient near the leading edge of the wing accreted with clear ice shows no significant change. However, there is a sharp decrease in the pressure coefficient on the upper surface of the wing, leading to a notable reduction in the wing lift coefficient after icing, which has a considerable impact on the aircraft's stability. The overall pressure coefficient of the wing accreted with glaze ice is similar to that of the clean wing model, consistent with the results shown in Figure 6. During the unsteady oscillatory ascent phase, the lift coefficients of the wing accreted with glaze ice and the clean wing model are essentially overlapping, highlighting the significant influence of the characteristics of glaze ice and clear ice. Therefore, research on the aerodynamic effects of different ice accretion shapes on aircraft wing profiles is essential. From Figure 9c, it can also be observed that as the oscillation angle decreases to α = −6.5° , the pressure coefficient near the leading edge of the wing accreted with clear ice is relatively high, while the pressure coefficient on the wing's lower surface is lower, contrasting with the distribution observed during the ascent phase. In comparison, the pressure coefficient distribution near the leading edge of the wing accreted with glaze ice shows minimal variation compared to the clean wing model. The comparison from Figure 9 reveals that the aerodynamic characteristics of the wing accreted with clear ice exhibit greater variability during unsteady oscillations, indicating a less stable performance. In contrast, the overall pressure coefficient of the wing accreted with glaze ice remains similar to that of the clean wing model, demonstrating more stable behavior with less variation.

Figure 9: Pressure coefficient contour maps at different oscillation angles. (a) α = 3.5° ↑ , (b) α =13.5° ↑ , (c) α =6.5°↓

Vorticity is one of the most important physical quantities describing vortex motion, defined as the curl of the fluid velocity vector. Vorticity contour maps provide a visual representation of vortex generation, development, and shedding throughout the entire pitching process [14]. Figures 10a-10c presents vorticity contour maps for two different ice shapes and a clean wing at various oscillation angles 3.5°, 13.5°, and -6.5° respectively. From Figure 10a, it is observed that at an oscillation angle of α = 3.5° , both the ice shapes attached to the wing exhibit larger vortical regions near the wing trailing edge and lower surface compared to the clean wing. Consequently, during unsteady oscillations of the iced wing surface, the distribution of adverse pressure gradient increases, resulting in a significant decrease in lift coefficient [15]. As the oscillation angle increases to α =13.5° Figure 10b, larger vortical regions are observed on the upper surface and rear section of the wing for the wing with clear ice attachment, correlating with increased drag coefficient and minimized moment coefficient, thereby impacting the aerodynamic characteristics of the aircraft. When the oscillation angle decreases to α = −6.5° Figure 10c, similar vortical patterns are observed for both clear ice and wedge ice attachments, with larger vortical regions on the lower surface and trailing edge. Compared to the clean wing, both ice shapes exhibit significant adverse pressure regions, adversely affecting the aerodynamic performance of the aircraft wing.

Figure 10: Vorticity contour maps at different oscillation angles: (a) α = 3.5° ↑ , (b) α =13.5° ↑ , (c) α =6.5°↓

Conclusion

This study conducted unsteady numerical simulations of pitch oscillations under three icing conditions on airfoil models, investigating the stall characteristics of iced airfoils and the variation of aerodynamic force/momentum coefficients with angle of attack. The hysteresis effect of aerodynamic coefficients during oscillations of iced airfoils was analyzed. The conclusions drawn are as follows: During unsteady oscillatory processes, the aerodynamic characteristics of the airfoil adhered with glaze ice exhibit more consistent effects, whereas those adhered with rime ice show highly unstable aerodynamic behaviors. Glaze ice poses relatively less detrimental effects on aerodynamic characteristics compared to rime ice, but it still significantly compromises aerodynamic performance.

The lift coefficient of the airfoil with adhered glaze ice is generally lower than that of the clean airfoil during the upstroke phase, with an average reduction of 7%. The maximum difference occurs at α = 6.5° . Throughout the downstroke phase, the lift coefficient of the airfoil with adhered rime ice is noticeably lower than that of the clean airfoil, with an average reduction of 7.5%. The maximum difference occurs at α = 7° . In contrast, the lift coefficient of the airfoil with adhered glaze ice exhibits significant variations within the angle of attack range from -3.5° to 8.5°, with an average reduction of 12%. The maximum difference occurs at α = 4° , constituting 10% of the total difference.

Glaze ice, characterized by its smooth and transparent texture, exhibits a more pronounced increase, with the overall average drag coefficient increasing by 2.1 times. Rime ice, known for its rough surface and propensity to shed, shows an increase of 1.5 times compared to the clean airfoil. Both ice formations significantly impact the aircraft's drag.

During unsteady oscillations, the wing with adhered ice formations exhibits more frequent occurrence of adverse pressure gradients and larger vortex regions compared to the clean wing surface. This directly disturbs and influences the aerodynamic characteristics of the aircraft wing. Therefore, during oscillatory processes, efforts should be made to simulate conditions where glaze ice and rime ice adhere to the wing surface to a greater extent.

References

1. Esmaeilifar E, Raj LP, Myong RS. Computational simulation of aircraft electrothermal de-icing using an unsteady formulation of phase change and runback water in a unified framework. Aerospace Sci Technol. 2022;130:107936.

   [Crossref] [Google Scholar]

2. Min S, Yee K. Numerical investigation of the unsteady effect owing to oscillation on airfoil icing. Int J Heat Mass Transfer. 2023;203:123791.

   [Crossref] [Google Scholar]

3. Shen X, Zhao W, Qi Z, Lin G, Wang L. Analysis of numerical methods for droplet impingement characteristics under aircraft icing conditions. Aerospace. 2022;9(8):416.

   [Crossref] [Google Scholar]

4. Verma N, Baloni BD. Influence of Reynolds number consideration for aerodynamic characteristics of airfoil on the blade design of small horizontal axis wind turbine. Int J Green Energ. 2022;19(7):733-746.

   [Crossref] [Google Scholar]

5. Wang Q, Zhao N, Wang TG, Zhong W, Wang L. Numerical simulation of wind turbine airfoil dynamic stall with transition modeling. Acta Energ Sol Sin. 2012;33(1):113-119.

   [Google Scholar]

6. Barlas TK, van Kuik GA. Review of state of the art in smart rotor control research for wind turbines. Progress Aerospace Sci. 2010;46(1):1-27.

   [Crossref] [Google Scholar]

7. Ingersoll B, Ning A. Efficient incorporation of fatigue damage constraints in wind turbine blade optimization. Wind Energ. 2020;23(4):1063-1076.

   [Crossref] [Google Scholar]

8. Jasa J, Glaws A, Bortolotti P, Vijayakumar G, Barter G. Wind turbine blade design with airfoil shape control using invertible neural networks. J Phys: Conferen Series. 2022;2265(4):042052.

   [Crossref] [Google Scholar]

9. Roman M. Repair and reinforcement of wind turbine blade edges. 2020;63(6):206-207.
10. Qi Y, Xu S, Huang D. Investigation on aerodynamic performance of horizontal axis wind turbine by setting micro-plate in front of the blade leading edge. Renewable Energ. 2021;179:2309-2321.

    [Crossref] [Google Scholar]

11. Ferrari JA. Influence of pitch axis location on the flight characteristics of a NACA 0012 airfoil in dynamic stall. Rensselaer Polytech Instit. 2012.

    [Google Scholar]

12. Danao LA, Qin N, Howell R. A numerical study of blade thickness and camber effects on vertical axis wind turbines. Proceed Instit Mech Eng Part A: J Power Energ. 2012;226(7):867-881.

    [Crossref] [Google Scholar]

13. Berton E, Allain C, Favier D, Maresca C. Experimental methods for subsonic flow measurements. Notes Numeric Fluid Mech Multidisciplin Design. 2002;81:97-104.

    [Google Scholar]             

14. Correa AF. The study of dynamic stall and URANS capabilities on modelling pitching airfoil flows. 2015.

    [Crossref] [Google Scholar]              

15. Kasibhotla VR, Tafti D. Large eddy simulation of the flow past pitching NACA 0012 airfoil at 1e5 Reynolds number. Fluid Eng Div Summ Meet. 2014;46216:8.

    [Crossref] [Google Scholar]