International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2018) Volume 9, Issue 3
This paper puts forward an improved K-SVD object detection algorithm for the problem of multiple noise sources in underground mine video. Firstly, the background modeling is applied in the video; then, the improved non-local mean filtering algorithm is used to enhance the image quality; finally, the improved image is processed by the sparse representation algorithm to further detect the moving object. In order to verify the effectiveness of the proposed algorithm, the algorithm and other algorithms are applied to video object detection in two different scenarios. The experimental results show that, in the underground mine video, the proposed algorithm can increase the accuracy by more than 8% compared with the traditional K-SVD algorithm, and the proportion of error points decreases by about 25%. Better detection of the moving object is achieved by the proposed algorithm.
Keywords: Underground mine; Background modeling; Image denoising; Sparse representation; Object detection; Non-local mean filtering
The purpose of moving object detection is to extract the foreground area that people are interested in in a video stream, that is, the moving object, in order to deal with the next step of object recognition, tracking, behaviour analysis and so on [1]. At the same time, the intelligent vision technology was introduced in the underground video surveillance system to further improve its digitalization and intelligence level, thereby reducing the injury and death rate of accident and ensuring the safety of coal mine production [2,3].
In recent years, domestic and foreign researchers have made intensive achievements in object detection. Morioka et al. [4] proposed to use colour histograms as regional features for matching, however, colour features are more affected by light and accordingly it is not robust. Bouzaraa et al. [5] proposed to use a statistical property of reference images to improve the accuracy of histogram matching, but the experiments were performed under outdoor conditions without considering the dim underground mine environment. Cong et al. [6] studied the background difference method of K-SVD (K-Singular Value Decomposition) [7,8] for dictionary learning, and achieved better detection results, but the ability to background model adaptive and anti-counterfeiting prospects is not strong enough, and not be suitable for low-illumination, high-noise underground mine complex environments. These detection algorithms only consider the illumination and noise changes in the outdoor environment and are not suitable for coal mine scenarios [9]. Therefore, for the characteristics of underground mine video, Wang et al. [10] proposed a combination of YOLOv2 (You Only Look Once, YOLO) and FCN (Fully Convolutional Networks) to improve the accuracy of underground mine small pedestrian detection, but there is a correlation between the accuracy of detecting small pedestrians and the speed of pedestrians for this algorithms. According to the characteristics of video underground mine, an algorithm for the linear fusion of colour and edge is proposed by Xian et al. [11]. It overcomes the detection problem of miners and background grey scale and can remove false moving objects caused by illumination changes. However, the detection threshold of the algorithm needs to be manually selected, and it is difficult to have the optimal results.
To sum up, this paper applies the sparse representation algorithm to the specific situation of underground intelligent video surveillance system. Considering the characteristics of the captured videos, an improved K-SVD by considering the non-local mean filtering algorithm is proposed. Major steps are: (1) the background is modelled. (2) The image to be detected is filtered to obtain a highquality object image, and the sparse representation algorithm is used to detect the moving object. (3) The video in different scenes is detected to verify the effectiveness of being proposed algorithm. Experimental results show that our new algorithm can be used to detect moving objects in underground mine video more accurately.
Image sparse representation
Sparse representation was originally proposed in the field of signal processing [12,13]. The core idea is to select a small number of basis vectors in a large number of base vector sets to represent the object signal and to obtain high compression ratio while ensuring high fidelity of the signal. The image sparse representation is to represent the image in the most concise way, that is, most of the coefficients are zero after expression, leaving only a few non-zero coefficients, and the non-zero coefficients can reveal the inherent structure and essential properties of the image.
Set the original signal x∈RM data dictionary D = [d1, d2, ..., dL] ∈RM x L where ddi(i = 1, 2, ...L), is atom of data dictionary. In this case, each signal can be represented as a linear combination of dictionary atoms, as shown in equation (1):
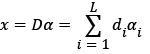 (1)
(1)
Where α = [α1, α2, ...αL]T is the sparse representation of the signal x , and also known as the sparse representation coefficients. If α has only a finite number of (such as k) non-zero elements, and all other elements are zero, then the sparsity of α is k . The signal x ∈ RM is sparsely represented by the dictionary D as shown in Figure 1.
The meaning of image sparse representation (also known as sparse coding) is that the coefficients represented by the dictionary are sparse, that is, only a small number of atoms are needed to uniquely represent the image linearly. Its mathematical model is expressed as:
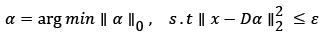 (2)
(2)
Where 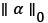 epresents the norm of l0 and is the number of zero elements in the α. ε refers to the sparse representation error and the error constraint term
epresents the norm of l0 and is the number of zero elements in the α. ε refers to the sparse representation error and the error constraint term 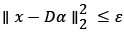 guarantees that the coefficient α is as close as possible to the original image signal x. Due to the nonconvexity of the norm of l0, the solution to this problem is essentially a NP-Hard combinatorial optimization problem [14]. At present, commonly used methods mainly include Basis Pursuit (BP) [15], FOCUSS [16], Matching Pursuit (MP) [17], and Orthogonal Matching Tracking (OMP) [18] etc. Among them, the BP algorithm solves the above problem by changing l0 into l1 the formula (2) can be rewritten as
guarantees that the coefficient α is as close as possible to the original image signal x. Due to the nonconvexity of the norm of l0, the solution to this problem is essentially a NP-Hard combinatorial optimization problem [14]. At present, commonly used methods mainly include Basis Pursuit (BP) [15], FOCUSS [16], Matching Pursuit (MP) [17], and Orthogonal Matching Tracking (OMP) [18] etc. Among them, the BP algorithm solves the above problem by changing l0 into l1 the formula (2) can be rewritten as
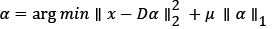 (3)
(3)
Where 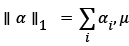 is called the penalty factor.
is called the penalty factor.
Dictionary learning
The sparsity of a signal is relative to its expression domain. In terms of image signals, it is usually not sparse in the spatial domain (pixel value), but in a specific dictionary, the expression of the signal become possibly sparse [19]. Therefore, whether or not the image signal can be sparsely represented depends largely on how the dictionary is constructed. There are two ways to construct a sparse representation dictionary [20]. The first type of method is a base dictionary. The dictionary is calculated by a mathematical model and represented by an implicit matrix. These types of dictionaries commonly use wavelet, curve wave, contour wave and other forms, but only when the characteristics of the signal match the dictionary, it can get better results; the second method is based on the learning method, through which a more specific dictionary can be constructed. Therefore, this paper also uses this method to construct the required dictionary. When constructing a dictionary, the atoms in it also need to meet two requirements: Firstly, in order to linearly represent the information in the M-dimensional space of the original signal, these dictionary atoms are required to form the entire M-dimensional space; secondly, in order to ensure uniqueness of signal sparse representation, it requires that each dictionary atom is linearly independent. The base dictionary method includes a Fourier transform dictionary, a discrete cosine transform dictionary, a wavelet transform dictionary, etc.; the learning class dictionary includes a principal component analysis dictionary, a K-SVD dictionary, an Independent Component Analysis (ICA) dictionary, and so on.
In practical applications, the corresponding dictionary design methods should be selected according to the actual situation. The choice of dictionary is generally divided into three cases: 1. when there is no training data, some transforms are used as a dictionary, that is, a base dictionary method; 2. if there is a large amount of training data, a learning class dictionary can be utilized. In this paper, the K-SVD dictionary learning algorithm is adopted. Firstly, the background is modeled, and then the detected image is processed by removing noise, and the BP algorithm in the sparse representation algorithm is used to solve the sparse coefficient of equation (3). Finally, the K-SVD algorithm is adopted. The error is calculated and the kth atom dk in dictionary D is updated, and the coefficient  corresponding to the kth row is also updated.
corresponding to the kth row is also updated.
Image denoising algorithm
Due to the low illumination, multi-noise and high noise in the mine environment, it has brought many difficulties to the detection of moving objects. Therefore, this paper proposes an Improved Non- Local Mean (INLM) filtering algorithm. First, the image is reconstructed by using the low-frequency coefficients of DCT to filter out some noise while protecting the main content of the image [21]. Then, use the Mahalanobis distance to improve the NLM algorithm [22], and the denoising processing was applied to the object, so that the image has better quality before detection. Finally, sparse representation was implemented, so as to improve the accuracy of moving object detection.
Discrete cosine transformation
DCT is an orthogonal transform whose transform kernel is a real cosine function. After discrete cosine transform of an image, much important visual information about the image is concentrated in a small part of the low-frequency coefficients of the DCT transform.
Given two-dimensional signal f of size N × N, its DCT is defined as:
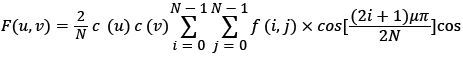
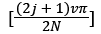 (4)
(4)
The Inverse Discrete Cosine Transform (IDCT) is defined as:
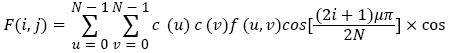
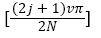 (5)
(5)
In the above formula
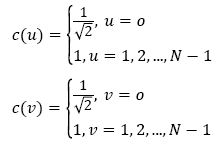
It is because the discrete cosine transform has a strong "energy concentration" characteristic, the reconstructed image reconstructed by a small number of low-frequency DCT coefficients can be used to replace the noise image to calculate the similarity weight value between the image blocks.
NLM algorithm
Classical NLM filtering, when filtering the additive noise image, the Gaussian weighted Euclidean distance between each pixel in the nonlocal large-scale searching window and the central pixel under a smallscale similar window was estimated. And the degree of similarity between the pixels and the center pixel was measured. This will be set as the main parameter for determining the size of each pixel weighting coefficient.
Given at position i , the observation value is X(i) , and useful signal is S(i) , then the additive noise image model is
x(i) = S (i) + N (i) (6)
Then, the classical NLM filtering algorithm performs non-local weighted average filtering on the image i position pixels, which can be described as
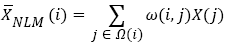 (7)
(7)
Where Ω(i) represents a large-scale search window centered on the center of i; ω(i, j) represents the weighting coefficient of j pixels to i pixels in the search window. The calculation of the weighting factor ω(i, j) can be expressed as
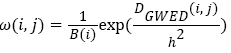 (8)
(8)
Where h refers to control the decay rate of the exponential function, it determines the degree of filtering; B(i) refers to the regularization factor and it can be expressed as
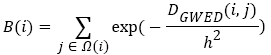 (9)
(9)
Where DGWED (i, j) represents the Gaussian weighted Euclidean distance between i pixels and j pixels in the search window of Ω(i), which can be expressed as
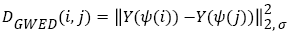 (10)
(10)
Where Y(ψ(i)) ψ(i) and represent small scale similar windows centered on i, j, respectively. Y(ψ(i)) and Y(ψ(j)) represent the image observation value matrix at the similar window ψ(i) and ψ(j) represents the Gaussian weighted norm with the calculated standard deviation of σ2.
Mahalanobis distance
The Mahalanobis distance proposed by Indian statistician Mahalanobis is a more effective and reliable method of measuring the similarity of sample data than the Euclidean distance. It overcomes the shortcomings of Euclidean distance. The Mahalanobis distance eliminates the interference of correlation between variables by standardizing the sample data, and more effectively measures the similarity between the sample data.
Assuming that the two sets of sample data i, j constitute the column vectors xi and xj, the Mahalanobis distance dij between the two vectors is defined as 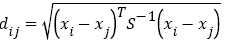 (11)
(11)
Where S is the covariance matrix of vectors xi and xj,
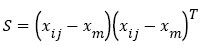 (12)
(12)
Where 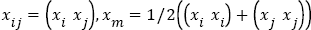 . It can be seen from equation (5) that when S is a unit matrix, the Mahalanobis distance degenerates to the Euclidean distance, so the Mahalanobis distance is an extension of the Euclidean distance.
. It can be seen from equation (5) that when S is a unit matrix, the Mahalanobis distance degenerates to the Euclidean distance, so the Mahalanobis distance is an extension of the Euclidean distance.
Generalizing calculation of Mahalanobis distance
When calculating the Mahalanobis distance, the inverse matrix of the covariance matrix S in equation (5) does not exist, so the Mahalanobis distance defined by equation (4) is unstable. To solve this problem, a generalized inverse matrix of S is introduced. By implementing singular value decomposition on equation (5), one obtains
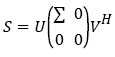 (13)
(13)
Where U, V matrix is unitary matrix. 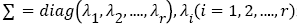 is a non-zero singularity of the matrix and
is a non-zero singularity of the matrix and 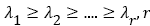 is the rank of S; and the superscript H indicates that the matrix is conjugate transposed. By solving Moore-Penrose inverse matrix S+ in equation (6), one gets
is the rank of S; and the superscript H indicates that the matrix is conjugate transposed. By solving Moore-Penrose inverse matrix S+ in equation (6), one gets
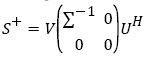 (14)
(14)
Where  . Equation (7) is a generalization of the feature space pair for S-1 by using S+ to substitute S-1 in Equation (4), one gets the Mahalanobis distance in the feature space
. Equation (7) is a generalization of the feature space pair for S-1 by using S+ to substitute S-1 in Equation (4), one gets the Mahalanobis distance in the feature space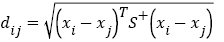 (15)
(15)
In the 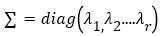 value of
value of 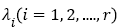 represents the amount of energy of each unrelated data component. For image data,
represents the amount of energy of each unrelated data component. For image data, 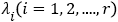 represents the variance of each irrelevant component information in the image. It was found that λ1 is always much larger than other values, i.e.
represents the variance of each irrelevant component information in the image. It was found that λ1 is always much larger than other values, i.e.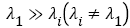 . When calculating, we can just keep λ1 and ignore
. When calculating, we can just keep λ1 and ignore 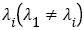 and think that other singular values are zero. This not only effectively reduces the data dimension, but also suppresses interference from non-useful signals, i.e. noise disturbance. According to the above analysis, one gets
and think that other singular values are zero. This not only effectively reduces the data dimension, but also suppresses interference from non-useful signals, i.e. noise disturbance. According to the above analysis, one gets
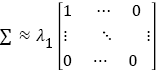 (16)
(16)
Invert the equation (9), one gets 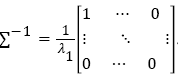 By substituting Σ−1 into equation (7) and deduce it, we can get
By substituting Σ−1 into equation (7) and deduce it, we can get
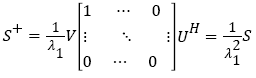 (17)
(17)
By substituting equation (10) into equation (8), we get improved Mahalanobis distance:
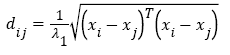 (18)
(18)
Equation (11) not only avoids the instability of the Mahalanobis distance, but also simplifies the calculation and suppresses the noise interference. Because of the symmetry of the Mahalanobis distance, symmetry can be used to halve the computational complexity without sacrificing denoising performance.
Background modelling
When the camera is fixed, the background area can be regarded as static, and only the pixel value of the position where the moving object is located will change. The successive frames are combined by column vector, and the background values of adjacent columns are equal if the interference of noise was ignored. At this time, the image in the current frame can be represented by the foreground object and the background image. Assuming that the current frame image is X , the background image is Xb, and the foreground image of the motion is Xf , then the image at this time can be expressed as:
X = Xb + Xf (19)
However, the actual image in underground mine generally has noise interference. Therefore, in the case of considering noise interference, the current image is composed of three parts. The mathematical expression is as follows:
X= Xb + Xf + XE (20)
Where EX is the error matrix caused by noise. The background model can be obtained by dictionary learning and updating. The problems of low illumination and multiple noise sources in the underground mine environment have brought many difficulties to the detection of moving objects. Therefore, this paper first uses the Improved Non-Local Means (INLM) filtering mentioned above to remove the noise of the detected object, so that the image has better image quality before detection. Then the sparse representation is applied to each image, so as to improve the accuracy of detection of the moving object. The background is initially modelled by constructing the minimization constraint function using following equations:
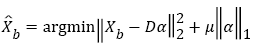 (21)
(21)
Where D is the data dictionary to be trained, and each column vector corresponds to a dictionary atom. The initial training dictionary D(0) and the sparse coefficient of the background image Xb decomposed on D are obtained by K-SVD. In equation (21), the first term is to ensure that the image can be approximated by a linear combination of the dictionary D and the coefficient α; the second term is a sparse control to ensure that the sparsest coefficients α are constantly sought during the solution. The product of the optimization object D and α is the initial background sparse representation model 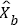 .
.
The above minimization algorithm requires an initial value of the background Xb, which is obtained by using a multi-frame averaging algorithm is obtained. The mean value of the P-frame training sample image is taken as the Xb initial value in equation (21), namely:
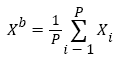 (22)
(22)
Where Xi (i= 1, 2, ...., P) represents the P frame training sample image.
Background update
After obtaining the initial background sparse representation model, five adjacent frames in the video sequence are extracted. The iterative update operation of the dictionary atom of dk and the sparse coefficient of α are completed by the K-SVD dictionary learning method. And the optimal data dictionary D is found. The background modelling based on the dictionary is optimally approximated to the observation value of the background modelling of the neighbouring frame image, thereby obtaining an updated optimal background model of 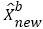 . That is,
. That is, 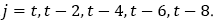 Therefore, the following optimization problem will be solved:
Therefore, the following optimization problem will be solved: 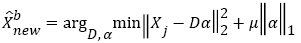 (23)
(23)
In the formula, 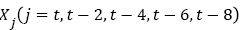 represents the five adjacent frames of the video sequence at time t.
represents the five adjacent frames of the video sequence at time t.
Background update algorithm
Input: video sequence of X to be detected, initial dictionary of D(0) and sparse coefficient of α.
Steps:
1. Five adjacent frames 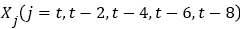 of the video sequence to be detected at time t were extracted. Set the iteration counter C, and its initial value is set as 1
of the video sequence to be detected at time t were extracted. Set the iteration counter C, and its initial value is set as 1
2. Dictionary updating: Based on equation (16), each atom  in dictionary D is updated step by step using the K-SVD dictionary learning method. Rewrite equation (23) as
in dictionary D is updated step by step using the K-SVD dictionary learning method. Rewrite equation (23) as
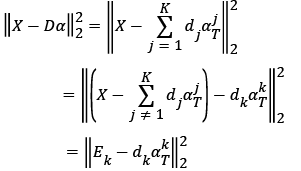 (24)
(24)
Where Ek: the error to the representation of the image caused by removing the atoms. In order to get the minimum value of the above formula, it is necessary to make 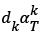 approaching Ek as close as possible. Therefore, the singular value decomposition is performed to Ek, so that
approaching Ek as close as possible. Therefore, the singular value decomposition is performed to Ek, so that 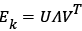 . The dictionary atom dk is updated by the first column of U, and the new coefficient
. The dictionary atom dk is updated by the first column of U, and the new coefficient 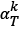 is obtained by V multiplying
is obtained by V multiplying 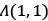 .
.
3. Let C = C + 1, If the C is less than the pre-defined cycle number, go to step 2, otherwise exit the loop Output: Updated optimal background model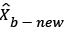
Determination of moving object.
After the background model is updated, the background modeling difference method of equation (20) is used to perform a differential operation between the current frame image X and the updated background model b new  to obtain a foreground moving object.
to obtain a foreground moving object.
 (25)
(25)
In the formula, T is the pre-defined threshold, and it is used to determine whether the pixel point belongs to the foreground object. If it is smaller than the threshold, it belongs to the background modeling.
In this paper, the software MATLAB is used to perform moving object detection experiments for video in two different scenarios. The first video comes from the PETS2001 (Performance Evaluation of Tracking and Surveillance) database. The video captures the pedestrian walking process and takes the common pedestrians in motion as the object to be tested. As can be seen from the video images, the image quality in this video is clear and not affected by the illumination changes. Figure 2 shows the 10th and the 100th frame of the video. It can be found in Figure 2, the illumination is uniform, and the image is not disturbed by excessive noise.
For the above video, the moving object detection is performed on the video by MoD algorithm, MOG algorithm, traditional K-SVD algorithm and the algorithm in this paper. The obtained results are shown in Figure 3.
It can be seen from the test results that the object detected by the MoD algorithm is very weak, and the object is hardly seen from the result. The MoG algorithm is more obvious than the MoD algorithm, but there is noise in the picture; for the traditional K-SVD algorithm, the same problem exists. Using the algorithm of this paper, the detected moving object contours and detailed results are clear and there is no noise interference.
The video used in experiment 2 was actually taken in the underground mine. The camera is located in the roadway. The object to be detected is also the pedestrian walking in the roadway. The 2nd and the 150th frame image in the video are shown in Figure 4. It can be seen from the video quality used in Experiment 2 is worse than the video quality in experiment 1. The images of video in experiment 2 have several problems such as uneven illumination and many noises.
Due to the uneven illumination and many noises in the underground mine video, the object to be detected will be interfered and affected by these problems. Therefore, the idea of this paper is to use less representative information to reconstruct the detected object. The selected representative information usually has better robust. Even in the case of more interference sources, these information can be well adapted to the complex environment of the underground mine, and can be applied to reconstruct the moving object stablely. Since the sparse representation algorithm uses less feature information for recovering the moving object. In this paper, the sparse representation algorithm was introduced to reconstruct the moving object in the underground mine environment.
For the experimental-2 video, the moving object detection is performed by MoD algorithm, MOG algorithm, traditional K-SVD algorithm and the algorithm in this paper. The obtained results are shown in Figure 5.
It can be seen from the test results in Figure 5, for underground mine video, the change of illumination and the interference of noise will have a corresponding impact on the detection result of the moving object. Figure 5(a) shows the detection results obtained by using the MoD algorithm. It can be seen from the results that due to uneven illumination and multi-noise F interference in the mine video, the detection result contains a lot of background scene information. Such detection results will bring great difficulties for subsequent further processing. Figure 5(b) shows the detection results of the MoG algorithm. It can be seen from the figure that the detection result of the MoG algorithm has been improved to some extent than the MoD algorithm. Most of the detection results are foreground information. Due to the noise interference, there exist some noise information, and the moving object also loses a part of the contour information. Figure 5(c) shows the detection results by using the traditional K-SVD algorithm. It can be seen that in the complex environment in underground mine, the sparse representation algorithm shows better robustness, and the detection results are obviously better than the above two algorithms. However, there is still a problem of noise interference and loss of object local information in the result. Figure 5(d) shows the detection results of the proposed algorithm in this paper. Since the filtering algorithm is applied in advance, the influence of the interference factor has been well eliminated. And the object is well detected with rich details. Results show that the detecting algorithm in this paper is significantly better than the previous three algorithms.
It can be seen from the above two experiments that although the two videos come from different scenes and environments, the algorithm proposed in this paper can detect the moving objects better in both the daily environment and the specific scenes in the underground mine. The detected objects have more detailed information, which provides a good basis for subsequent motion recognition and tracking.
The above results visually illustrate the superiority of the proposed algorithm over the other three algorithms. In order to compare the different detecting algorithms quantitatively, Tables 1 and 2 present the detection error and detection precision, respectively. In this paper, TP is used to indicate the correct number of front attractions, TN is the number of correct background points, FP is the number of wrong front spots, and FN is the number of wrong background points. Therefore, the effectiveness of the proposed can be explained by parameters of PBC and Precision.
| Video | MoD | MoG | Traditional K-SVD | This paper |
|---|---|---|---|---|
| Video 1 | 0.44376 | 0.42142 | 0.40751 | 0.38055 |
| Video 2 | 0.78722 | 0.56325 | 0.55694 | 0.30471 |
Table 1: Comparison of PBC for different detecting algorithms.
| Video | MoD | MoG | Traditional K-SVD | This paper |
|---|---|---|---|---|
| Video 1 | 0.74557 | 0.80113 | 0.81353 | 0.87355 |
| Video 2 | 0.63674 | 0.80429 | 0.81637 | 0.89751 |
Table 2: Comparison of detecting precision for different detecting algorithms.
PBC indicates the proportion of the error points in the object detection. The smaller the value, the higher the accuracy of the segmentation. That is to say, the result of the detection of the moving object is that the wrong pixel is the least. Precision indicates the proportion of the correct number of front attractions in the detected foreground. The higher the value, the more accurate the detected foreground. The calculation results of the PBC and the foreground segmentation precision (Precision) of the four algorithms in the two experiments are shown in Tables 1 and 2.
As can be seen from Table 1, in the 1st experiment, since the image quality of the video used is high, the calculation results of the four algorithms in the PBC are relatively similar. However, for the video used in the 2nd experiment, due to the complexity of the underground mine environment, the video has uneven illumination and many noises. From the PBC calculation results for 2nd experiment, the detection algorithm in this paper obviously better than the other three algorithms.
The comparison of object detection precision for different four algorithms is presented in Table 2. For the 1st experiment, because the video quality is high, the four algorithms can detect the foreground object well, and the calculated accuracy is also very similar. However, in the 2nd experiment, the quality of the video image decreased linearly. Therefore, the detection accuracy also decreased. Especially the calculation result of the MoG algorithm decreased by nearly 0.11. However, the accuracy of the proposed algorithm in this paper did not decrease, and the proportion of error points has not increased. Which indicates that the algorithm in this paper has strong adaptability and effectiveness in certain complex dark situations?
The algorithm proposed in this paper is aimed at the specific scene of the underground mine environment. The video in this scene has problems such as uneven illumination and more noise. Therefore, this paper uses the improved non-mean local filtering algorithm to filter the object to improve the image quality. Then the sparse representation is introduced into the underground mine video, and the moving object has been well detected. Results in this paper show that the sparse representation algorithm has good robustness in the underground mine environment, and the proposed algorithm can overcome the problems of illumination and noise interference in the underground mine environment. The object detection algorithm provides a solid foundation for the next step of moving object recognition and tracking.