Entropy S attains a maximum in an isolated system (i.e., with given internal energy and volume) at thermodynamic equilibrium. According to Gibbs, the macrostate which is most likely to be observed includes the largest number of microstates; the latter are equiprobable because of Liouville’s theorem of mechanics.

As for steady states far from equilibrium, the amount of entropy produced per unit time by all irreversible processes (“entropy production”) is a minimum against simultaneous perturbations of thermodynamical fluxes and forces (Minimum Entropy Production, MEP) in non-isolated, discontinuous systems where Onsager symmetry holds. (A system is discontinuous if we may split it in many mutually interacting regions, the entropy density being uniform in each region). If either forces or fluxes are fixed, then MEP is replaced by the least dissipation principle, i.e. maximisation of the difference between entropy production and Rayleigh’s dissipation function [1]. Unfortunately, Onsager symmetry relies on very stringent assumptions [2] which hold e.g. in solid-state physics [3]. In continuous systems (where entropy density is a continuously varying function of space) Onsager holds for particular problems only, like e.g. particle diffusion coupled with chemical reactions whose chemical affinity is much lower than thermal energy [4]. MEP predicts self-organisation in simple networks of autocatalyic chemical reactions [5], and has been also applied to radiative transport [6]. But MEP provides no correct predictions in simple problems of heat transport, Ohmic heating [7] and fluid dynamics [8].

Alternative approaches are extensively investigated. Kirchhoff has shown that Ohmic heating power gets minimized in steady state electric conductors at constant resistivity [9]. This result reduces to Steenbeck’s principle for electric arcs [10], and has been postulated for electron-positron plasmas in [11]. Moreover, it has been shown [12] that viscous power is minimised in viscous, steady, Newtonian fluids [13] at low Reynolds’ number [14]. Chandrasekhar has proven constrained minimisation of Rayleigh’s number in many problems involving Bénard convection cells [15].

Some researchers have also postulated variational principles in order to get closure conditions in the description of steady turbulence. Busse invokes maximisation of the amount of momentum transported by convection in turbulent Couette flow [16]. Malkus maximizes the total rate of energy dissipated per unit mass in steady-state, viscous, incompressible turbulent shear flows with fixed averaged velocity [17]. Paltridge’s maximisation of the averaged amount of entropy produced per unit time by energy exchange between equatorial and polar regions of Earth’s atmosphere [18] is generalised in [19,20] and extended to further problems in turbulence in [20,21]. In contrast with MEP, all these approaches maximise the entropy produced per unit time, and are collectively known as MEPP (Maximum Entropy Production Principle). Examples of MEPP may be found also outside fluid dynamics, like the “orthogonality principle” postulated in [22] for problems of plasticity, as well as the applications to crystal growth [23].

Unfortunately, no generally accepted proof of MEPP exists to date. Attempts to derive MEPP are unconvincing since they often require introduction of additional hypotheses, which by themselves are less evident than MEPP itself. For example, the orthogonality principle of [22] has its statistical substantiation only if the deviation from equilibrium is small [23]. MEPP holds for selected problems only. For example, some transport properties in fluids which satisfy MEP satisfy maximisation criteria [24]. Kirchoff’s result defies universal MEPP validity, and it is possible to reconcile Steenbeck’s principle with MEPP for linear laws only [25].

An approach to MEPP for selected problems involving the amount of entropy produced per unit time by irreversible processes across the boundaries of the system is discussed in [26] and includes the results of [15], [17] and [21]; it has been applied to the transition to turbulence in viscous, turbulent, incompressible Couette flow [27]. In contrast, a popular approach (‘MaxEnt’ = Maximum Entropy) is to link MEPP with the maximisation of entropy (not of entropy production) within the so called ‘information thermodynamics’ developed by Jaynes [28,29]. We are going to discuss a particular application of MaxEnt to fluid dynamics below.

Maximisation of suitably defined “entropy” for steady, farfrom- equilibrium states is nothing new. In many problems where turbulence leads to spontaneous formation and self-sustainment of discrete, coherent structures like vortices, filaments and the like [30], the distribution of such structures at a given time plays the role of Gibbs’ microstate at thermodynamic equilibrium. This formal analogy allowed researchers to define an “entropy”, whose maximum corresponds to the most probable configuration of the system as a whole. Constraints are e.g. given by conservation of total energy, etc. For example, steady tokamak plasmas are described as a constrained maximum of the entropy built on a system of toroidal filaments of electric current, the constraint being given by a fixed value of total electric current [31]. A similar approach to 2D magnetohydrodynamic steady turbulence leads to a correct dimensional analysis of transport coefficient in turbulent plasmas [32,33]. It is even possible to introduce the equivalent of absolute temperature T, which may become negative in case of self-organisation. However, this “temperature” is model-dependent; this feature is in common e.g. with the ‘Extended Irreversible Thermodynamics’ [34].

MaxEnt looks for the description of the system which requires a minimum amount of information given the constraints provided by experiments and/or general symmetry considerations like e.g. energy conservation. The aim is to obtain the best estimates that can be made on the basis of the information available, independently of any physical argument. Dewar [35,36] derived MEPP from Jaynes’ results; his proof is criticised in Sec. 2.3.4 of [23] and in [37], and its validity is limited to the contributions of some irreversible processes only to the entropy production [38]. Niven links MaxEnt and a control volume approach [39]; Niven’s work is criticised in [26]. Dewar’s argument [38] is similar to Gibbs’ treatment of equilibrium: the difference is that the “entropy” is not defined by a probability measure on phase space, but on path space. A “path” is an allowable trajectory for the system which evolves across the phase space in time, or, in other words, a microstate of the evolution of the system. A macrostate is a set of time dependent values of few macroscopic quantities. Many microstates correspond to one macrostate, just like in Gibbs’ thermodynamics. The most likely evolution of the system maximizes an “entropy”, which is built starting from the paths. In MaxEnt, a macroscopic steady system far from equilibrium is equally likely to follow any of its paths–see equation “qi=s−1” page 021113-2 of [39]. At equilibrium, microstates are equiprobable because of Liouville equation; unfortunately, no Maxent equivalent of Liouville equation is stated explicitly. This agrees well with Jaynes’ philosophy, but casts doubt on the physical relevance of MaxEnt.

As an example, we discuss an application of MaxEnt to a 2D incompressible flow behind a circular cylinder with Reynolds number 100 [40]. Meaningful physics is invariant with respect to scaling transformations, like those involved when changing the system of units from SI to CGS [41]. Constraints like energy conservation are automatically scale-invariant: regardless of the actual value of the total energy E_TOT, relationship E=E_TOT is scale-invariant because if E → λE (with λ ≠ 0) then also E_TOT → λE_TOT for dimensional reasons. Physics does not depend on λ; indeed, equation (3.17) of [40], which plays the role of energy conservation, is scale-invariant. Now, let us suppose we find a configuration which maximizes an “entropy” H while using a system of units where λ=1. The condition H=max. implies dH/dλ=0 for λ=1. Together, “entropy” maximization and scale invariance require:

                      H=max. and dH /dλ=0 for arbitrary λ            (1)

Conditions (1) are automatically satisfied at thermodynamical equilibrium, where H=S depends on E through Boltzmann’s exponential exp(-E/k_BT), kB Boltzmann’s constant; if E → λE then k_BT → λ k_BT for dimensional reasons. In contrast, the treatment of [40] violates (1). In fact, equations (3.8), (3.14) and (3.15) of [40] show that H depends just on a subset the coordinates of the system, namely on those responsible for the occurrence of coherent structures in the fluid. For the sake of clarity, let us suppose H to depend just on 2 quantities a1, a2; generalization is straightforward. We follow § 5 and equation (3.14) of [40], recall that both a₁ and a₂ have the dimension of a velocity, take a₂=α a₁² where the constant α has the dimension of 1/velocity, and eliminate therefore the dependence of H on a₂.

According to (3.8), we write 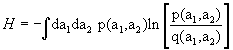where p and q are suitable quantities with dimension of 1/velocity2. Of course dH/dλ=0, but what about H = max.? Taking a₂=α a₁² requires that we write 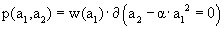and 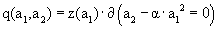where both functions w and z have dimensions 1/velocity. Accordingly, 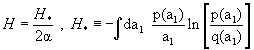where we recall that 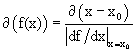if f(x = x₀) = 0. The condition H = max. is therefore equivalent to H* = max.; but dH* /dλ ≠ 0 because H* has the dimension of 1/velocity, and (1) is violated. MaxEnt makes the separation between coordinates of coherent structures and other coordinates to violate scale-invariance even if H is scale-invariant.