Research into carbon nanocones (CNC) started almost at the same time as the discovery of carbon nanotube (CNT) in 1991. In resent years, nanostructures involving carbon have been the focus of an intense research activity, which is driven to a large extent by the quest for new materials with specific applications. Ball studied the closure of (CNT) and mentioned that (CNT) could sealed by a conical cap, [1]. The official report of the discovery of isolated CNC was made in, 1994 when Ge and Sattler reported their observations of carbon cones mixed together with tubules an a flat graphite surface [2]. This are constructed from a graphene sheet by removing a 60º wedge and joining the edges produces a cone with a single pentagonal defect at the apex. If a 120º wedge is considered then a cone with a single square defect at the apex is obtained. the case of 240º wedges yields a single triangle defect at the apex [3-5].

Topological indices are graph invariants and are used for Quantitative Structure - Activity Relationship (QSPR) and Quantitative Structure - Property Relationship (QSPR) studies, [6-8]. Many topological indices have been defined and several of them have found applications as means to model physical, chemical, pharmaceutical and other properties of molecules.

A topological index of a molecular graph G is a numeric quantity related to G. The oldest nontrivial topological index is the Wiener index which was introduced by Harold Wiener. John Platt was the only person who immediately realized the importance of the Wiener’s pioneering work and wrote papers analyzing and interpreting the physical meaning of the Wiener index.

We now recall some algebraic definitions that will be used in the paper. Let G be a simple molecular graph without directed and multiple edges and without loops, the vertex and edge-sets of which are represented by V(G) and E(G), respectively. The vertices in G are connected by an edge if there exists an edge uv∈E(G) connecting the vertices u and v in G so that u,v∈V(G). In chemical graphs, the vertices of the graph correspond to the atoms of the molecule, and the edges represent the chemical bonds. The number of vertices and edges in a graph will be defined by |V (G)| and |E (G)| respectively. In graph theory, a path of length n in a graph is a sequence of n+1 vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A vertex is external, if it lies on the boundary of the unbounded face of G, otherwise, the vertex is called internal.

The distance d_G (u,v) is defined as the length of the shortest path between u and v in G. D(u) denotes the sum of distances between u and all other vertices of G. For a given vertex u of V(G) its eccentricity, ecc (u), is the largest distance between u and any other vertex v of G. The maximum eccentricity over all vertices of G is called the diameter of G and denoted by Diam(G) and the minimum eccentricity among the vertices of G is called radius of G and denoted by R (G) and for any vertex u, Su is the sum of the degrees of its neighborhoods and degG (u) denotes the degree of the vertex u.

The Wiener index [9] is one of the most used topological indices with high correlation with many physical and chemical indices of molecular compounds. The Wiener index of a molecular graph G, denoted by W(G), is defined

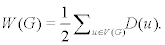
The eccentric connectivity index of the molecular graph G, 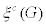was proposed by Sharma. V and Gosvami [4]. It is defined as

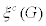
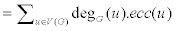
The modified eccentric connectivity index (MEC) is defined as.

Recently, Ediz et al. [10] introduced a distance-based molecular structure descriptor, the reverse eccentric connectivity index defined as,

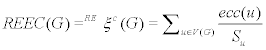
In this paper by using an algebraic method, we calculate the reverse eccentric connectivity index of one tetragonal carbon nanocones.

Let 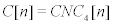. Our notation is standard and mainly taken from standard books of graph theory and the books of Trinajestic and Kumar [11,12]. In this section, the reverse eccentric connectivity index of C[n] are calculated. To do this, the following lemmas are necessary.

Lemma

,

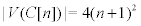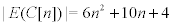
Proof. It is clear.

Lemma

,

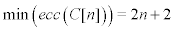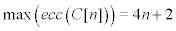
Proof . Suppose u is a vertex of the central square of S . Then from Figure 1 one can see that there exists a vertex v of degree 2 such that 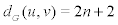and so 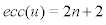. On the other hand, there exists another vertex w of degree 2 such that 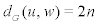. Therefore, the shortest path with maximum length is connecting two vertices of degree 2 in C[n]. This complete the proof.

Figure 1: A maximum and minimum path for computing ecc(u) in CNC₄[3].

The proof of Lemma 2.2, shows that the eccentricities of vertices of C[n] are varied between 2n+2 and 4n=2. Furthermore, we observe that there are two types of vertices in C[n]. 4n2 internal vertices of degree 3 have eccentricities between 2n+2 and 4n and 4n external vertices of degree 3 and 4n + 4 external vertices of degree 2 have eccentricities between 3n+2 and 4n+2.

Now we use an algebraic method for computing the eccentric connectivity of C[n]. For this purpose we consider two cases. The first case when n is an odd number and the second case when n is an even number. From Figure 2 when n is an odd number, the external vertices of C[n] are made of 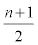types of vertices of degree 3 with eccentric connectivity equal to 3n + 2 + 2k and 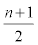types of vertices of degree 2 with eccentric connectivity equal to 3n + 3+ 2k for 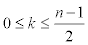But from Figure 3 when n is an even number, the external vertices of C[n] is made of 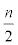type vertices of degree 3 with eccentric connectivity equals to 3n + 3+ 2k for 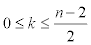and 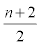type vertices of degree 2 with eccentric connectivity 3n + 2 + 2k for . Also, we observe that there are four types of vertex neighborhoods in C[n]. For all internal vertices, the product of their neighbors degrees is equal to 27. Then, there are 4n external vertices of degree 3 such that for all of them, the product of their neighbors degrees is equal to 12. There are exactly 8 external vertices of degree 2 such that their neighbors are of degrees 2 and 3 and for all of them, the product of their neighbors degrees is equal to 6. Finally, there are 4n-4 vertices of degree 2 such that both neighbors of them are of degree 3.

Figure 2: The eccentric connectivity of CNC₄ [3].

Figure 3: The eccentric connectivity of CNC₄ [2].

In the following theorem, the reverse eccentric connectivity index of C[n] is computed when n(≥ 1) is an odd number.

Theorem: The reverse eccentric connectivity index of C[n] is given by :

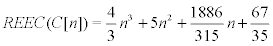
where n(≥ 1 ) is an odd number.

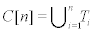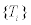Proof. With respect to Figure 2 where is a partition of the molecular graph C[n]. We have 4 types of vertices for every section of T_i . There are 8 vertices of type 1 with maximum eccentric connectivity 4n+2 and Su=5. Also there are 8(n-2l-2) vertices of type 2 when 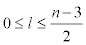. The eccentric connectivity of 4(n − 2l − 2) vertices of them equals to 3n-2l and the eccentric connectivity of other vertices equals to 3n −1− 2l . For l ≤ k ≤ l +1, if k − l = 0 then we have 8 vertices with Su =7 and 8k vertices with Su = 9. Also if k − l =1 then we have 8 vertices with S_u = 6 and 8k vertices with S_u = 9 such that the eccentric connectivity of them is equals to 4n +1− k − l when 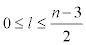. Also we have 4 vertices with Su = 7 and 4n-4 vertices with Su = 9 and ecc(u) = 3n + 2 and 4n vertices with S_u = 9 and ecc(u) = 3n +1. Thus we have

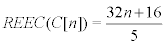
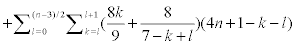
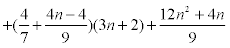
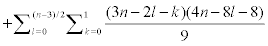
Now with a calculation in Matlab software we have

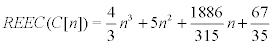
In the following theorem, the reverse eccentric connectivity index of C[n] is computed where n(≥ 2) is an even number.

Theorem: The reverse eccentric connectivity index of C[n] is given by :

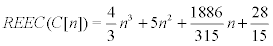
where n(≥ 2) is an even number.

Proof. With respect to Figure 3, 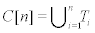, where 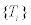is a partition of the molecular graph C[n]. We have 4 types of vertices for every section of T_i. We have 4 vertices with Su=6 and 4n vertices with Su=9 of type 1 with mean eccentric connectivity 3n=2 and 8(n-2l-1) vertices () with S_u=9 of type 2, such that the eccentric connectivity of 4(n-2l-1) vertices of this type is equals to 3n +1− 2l and the eccentric connectivity of other vertices of this type is equals to 3n − 2l . For l ≤ k ≤ l +1, if k − l = 0 then we have 8l+8 vertices with Su=9 and 8 vertices with Su=6. Also if k − l =1 then we have 8l + 8 vertices with S_u=9 and 8 vertices with S_u=7 ecc(u) = 4n −l − k when 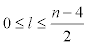. Also we ave 8 number of vertices with Su=5 and ecc(u) = 4n + 2 and 8 vertices with Su=7 and ecc(u) = 4n +1. Thus it implies that :

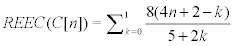
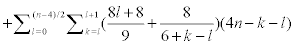
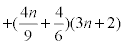
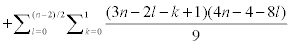
Now with a calculation in Matlab software we have