Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
ISSN: 2157-7544
Review Article - (2016) Volume 7, Issue 2
Accurate determination of brine density is crucial for an efficient designing of various systems through where brine take an undeniable part. The importance of determining brine density is well corroborated by recent ongoing research surge in this scope. Despite existence of several experimental and empirical approaches, a reliable and robust model seems to be requisite for precise determination of brine density. In regard to high performance and great robustness of soft computing approaches for unraveling science and engineering problems, this article proposes LS-SVM and MLP-NN models to determine the brine density. Both models are developed over 1868 data points including both natural and synthetic brines. The proposed models take account an extensive range of input parameters such as temperature, pressure, and concentration. The developed models can significantly estimate the target values with respect to high values of R2, which are 0.999999 and 1.000000 for MLP-NN and LS-SVM models, respectively. Considering high accuracy and swiftness of proposed models, they can be great assets to science and engineering scopes.
Keywords: LS-SVM; MLP-NN; Model; Brine density; Natural and synthetic brine.
AARD: Average Absolute Relative Deviation; ANFIS: Adaptive Neuro-Fuzzy Inference System; ARD: Average Relative Deviation; ANN: Artificial Neural Network; LS-SVM: Least Square Support Vector Machine; MLP-NN: Multilayer Perceptron Neural Network; MSE: Mean Squared Error; RMSE: Root Mean Square Error; STD: Standard Deviation Errors; N: the Number of data points
Nowadays, brines properties play a pivotal role in various engineering and scientific scopes including chemical, physical, geochemical, and geothermal domains. More specifically, these researches are mostly accomplished around fluid inclusion surveys, CO2 sequestration, water desalination, studies of fluid-rock interaction, fluid flow simulation and enhanced oil recovery (EOR) [1-3]. Take for instance drilling industry, which is well recognized as a costly operation, most of drilling fluids categorized as water based fluids are whether built on the basis of brine or in evident contact with salt formations, either ways the brine density take an undeniable part during the whole drilling procedure. Conventionally, a drilling operation faces serious challenges, which are in close relation with brine density and solubility through the fluid [4]. In other words, the brine density can be a representative index of well overhead pressure as well as affecting numerous parameters such as pH, contaminations (Ca++, Mg++), shale swelling problem, wash out problem, waste management, etc. Therefore, by determining the brine density precisely not only can we pave the way for a safe and secure operation but also we can manage different problems appropriately. Moreover, brine completion fluid has widespread application in completion and workover operations [5]. Generally, such fluids own high density to provide high fluid column hydrostatic pressure as well as overcoming high formation pore pressure. The aforesaid fluid should be solid free, thus the defined fluid weight should be obtained from saturated salts solutions including CaCl2, CaBr2 and ZnBr2 [6]. The effect of temperature, pressure, and concentration on the brine properties is undeniable. Thus, precise estimation of brine density is pressure, which cause overbalance condition but also to avoid high cost of expensive completion fluid due to its overproduction in case the well experiences serious loss through the formation. In addition, the phase equilibrium and PVT properties of the CO2-NaCl–H2O system have been investigated broadly since it has extensive applications in geochemical processes [7,8]. A wide research effort in determining PVT properties of CO2-NaCl–H2O geological fluids in industrial processes including the oil and gas production, Enhanced Oil Recovery (EOR), natural gas clathrate engineering, geothermal exploitation, the exhaust gases treatment, supercritical fluid extraction and oxidation, wastewater and waste liquids, fertilizers, and seawater desalination, etc. vouches for the fact that recent interests are developing around PVT behavior of CO2-NaCl–H2O geological fluids [9]. Interestingly, obtaining precise PVT properties of brine is requisite for avoiding errors in prediction of other petroleum parameters [10]. As a matter of the fact, with a recent considerable growth in oil production rate, the amount of brine production increases accordingly. There is no doubt that managing such a great amount of produced brine requires a tremendous cost. More elaborately, aquifers are the available water surround hydrocarbon reservoirs and assist the reservoir to produce robustly in various ways: peripheral water drive, edge water drive, and bottom water drive [11]. Through so-called water drive approach the new wave of brine pushes the hydrocarbon and increases the reservoir pressure in order to produce with a higher flow rate. Unfortunately, brine may also be produced in conjunction with hydrocarbon. The required not only to prevent inaccurate determination of overhead pressure, which cause overbalance condition but also to avoid high cost of expensive completion fluid due to its overproduction in case the well experiences serious loss through the formation. In addition, the phase equilibrium and PVT properties of the CO2-NaCl–H2O system have been investigated broadly since it has extensive applications in geochemical processes [7,8]. A wide research effort in determining PVT properties of CO2-NaCl–H2O geological fluids in industrial processes including the oil and gas production, Enhanced Oil Recovery (EOR), natural gas clathrate engineering, geothermal exploitation, the exhaust gases treatment, supercritical fluid extraction and oxidation, wastewater and waste liquids, fertilizers, and seawater desalination, etc. vouches for the fact that recent interests are developing around PVT behavior of CO2-NaCl–H2O geological fluids [9]. Interestingly, obtaining precise PVT properties of brine is requisite for avoiding errors in prediction of other petroleum parameters [10]. As a matter of the fact, with a recent considerable growth in oil production rate, the amount of brine production increases accordingly. There is no doubt that managing such a great amount of produced brine requires a tremendous cost. More elaborately, aquifers are the available water surround hydrocarbon reservoirs and assist the reservoir to produce robustly in various ways: peripheral water drive, edge water drive, and bottom water drive [11]. Through so-called water drive approach the new wave of brine pushes the hydrocarbon and increases the reservoir pressure in order to produce with a higher flow rate. Unfortunately, brine may also be produced in conjunction with hydrocarbon. The more the reservoir produces, the lower the reservoir pressure becomes and the more the brine will be produced. The production of brine along with hydrocarbon would have an adverse effect on the produced hydrocarbon both qualitatively and quantitatively [12]. This would even cause well shut-in due to lack of appropriate surface treatment. It is important to note that in some cases even in reservoirs enjoying most recent modern approaches the produced fluid contains more than 90% brine in volume [13]. Furthermore, it is contented by many recent research surveys that the hydrocarbon recovery through the water flooding approach can be boosted by means of adjusting the salinity of injected brine [14]. To this end, brine properties should be determined with the utmost accuracy. The most outstanding properties are density, viscosity, and solubility. Getting acquainted with aforementioned properties is crucial for evaluating the effect of volume and movement of water in the reservoir, wellbore, and through the surface facilities [15]. In general, widespread applications of brine properties in other fields induce a vast surge in literature to be engendered elaborately [16-19]. The properties of brine can be obtained through different approaches including laboratory experiments, available models and correlations, and also soft computing methods. Actually, laboratory studies were recognized to be the most solid and precise method. Nevertheless, this approach was found to be expensive and timeconsuming [20]. Thus, in the absence of laboratory experiments, other methods such as implementing empirical models and correlations were preferred to determine brine properties. However, these models are suffered from uncertainties and limitations [21]. All in all, apart from the time and cost issues, the success of different vital operations pivots on implementing the right approaches. Hereupon, the power of economy in associate with high degree of accuracy expected for determination of brine properties force us to seek for new alternatives to fulfill this demand. In following a review of all mentioned methods is provided.
Determination of brine properties
Basically, there are three main approaches appertain to determination of brine properties.
1- Methods, which are on the basis of laboratories surveys;
2- Methods, which link the brine properties to the empirical correlations; and
3- Methods, which are based on soft computing analysis.
These three approaches are discussed further below.
Laboratorial studies
Thus far, extensive experimental studies have been conducted to determine brine density in a wide span of temperature, pressure, and concentration. Gibson and Loeffler [22] reported the specific volume of brine for temperatures between 29815.15 and 385.15 K, pressures from 0.1 to 100 MPa, and salinity from 5 to 25 wt% NaCl. Hilbert [23] accomplished a massive research work to measure the specific volume of brine for temperatures, pressures, and salinities from 293.15 to 673.15 K, 10 to 400 MPa, and from 0 to 25 wt% NaCl, respectively. Ghafri et al. [24] reported the density of NaCl (aq) in a temperature range between 283 and 472 K and pressures up to 68.5 MPa and molality of 1.06, 3.16, and 6 mol/kg. In a similar attempt, Kumar [25] measured the density of SrCl2 (aq) for temperatures of 323.15 to 473.15 K and at pressure of 202.7 MPa and for concentrations up to 2.7 mol/kg. Pitzer et al. [26] conducted an experimental study to measure the densities of MgSO4 and Na2SO4 up to 470 K, 10 MPa and 1 m ionic strength. Similarly, Obsil et al. [27] examined densities of Na2SO4 (aq) and K2SO4 (aq) using vibrating-tube densitometry at temperatures from 298.15 K to 572.7 K and pressures up to 30.7 MPa as well as at concentrations of 0.01 mol/ kg to 1.0 and 0.5 mol/kg, respectively. Moreover, the density of NaCl (aq) and other salts were reported by Gates and Wood [28] from 0.1013 to 40 MPa and temperature of 298.15 K and in a concentration range of 0.05 to 5.0 mol/kg. Crovetto et al. [29] measured the vapor pressure and density of NaCl (aq) at temperature of 623 K and at molalities of 0.25, 0.5, 1, and 3 mol/kg. Sharygin et al. [30] investigated the densities of aqueous solutions of Na2CO3 and NaHCO3 for temperatures in a range of 298 K to 623 K and pressures up to 28 MPa and with molalities from 0.1 mol/kg to 1.0 mol/kg implementing vibrating-tube flow densimeter. Further experimental research efforts can be found elsewhere in open literature [31-35].
Empirical correlations
Hass [36] presented a model to estimate the density of vaporsaturated NaCl (aq) applying the empirical Masson’s Rule. This model is applicable to predict density in a temperature range of 348.15 to 598.15 K and up to saturation of 7.3 molal. Similarly, Philips et al. [36] brought forward a model to determine brine density for temperatures, pressures, and malalities of 283.15 to 623.15 K, up to 50 MPa, and 0.25 to 5 mol/kg, respectively. This model can predict the experimental values with maximum uncertainty of ± 2%. In another attempt, Rogers and Pitzer [37] conducted a very elaborated computational research to introduce a semiempirical model in order to explain thermal properties of NaCl (aq) for concentration range of 0.1 to 5 molal as well as determine volumetric data for temperatures from 273.15 to 573.15 K and pressures of 0 to 100 MPa. As a result, they provided comprehensive reports for values of expansivity, specific volume, and compressibility versus temperature, pressure, and molality. Ghafri et al. [1] developed an empirical model to predict the density, apparent molar volume, and isothermal compressibility of various brines employing corresponding experimental data. They were taking into account the whole range of experimental data including temperature, pressure, and malality. Bahadori et al. [38] presented an Arrhenius type function to discern the different characteristics of reservoir brine such as density, vapor pressure, and enthalpy over a wide range of 5-25% salt content by mass, and temperatures above 303.15 K. The aforementioned model enjoys lower roundoff error by excluding massive complexities of mathematics and provided in a pretty user-friendly configuration. More correlations are available in literature [39,40].
Soft computing techniques
Nowadays, soft computing approaches are well recognized as beneficial robust tools, which take a significant part in analyzing and unraveling challenging problems in various scopes of science and engineering (for instance [41-46]). The preponderance of these computer based approaches includes determining a target function with high degree of precision compared to many published empirical and analytical solutions [47,48].
Intelligent methods including the artificial neural network (ANN) [49-51], Adaptive Neuro-Fuzzy Inference System (ANFIS) models [52,53], Least Square Support Vector Machine (LS-SVM) [54-56], Multilayer Perceptron Neural Network (MLP-NN) [45,57-59], and Radial Basis Function Neural Networks (RBF-NN) [60-62] are amazingly robust and reliable tools for data analysis and interpretation that can be employed to predict regression and classification problems.
LS-SVM and MLP-NN as intelligent methods have been satisfactorily implemented in many scopes of science and engineering to unravel very complexes computational challenges; a fact evidently acknowledged by recent researches organized around investigating PVT properties of reservoir hydrocarbons [54,55,63,64], pressure gradient estimation of multiphase flow [65,66], and retention and solubility determinations [67,68]. In addition to previous domains, Arabloo et al. [69] proposed a LS-SVM algorithm to estimate properties of reservoir brine including liquid saturation vapor pressure, density and enthalpy. The model results were in acceptable agreement with the experimental data regarding the R2 value of 0.999. Moreover, Kamari et al. [70] presented an analogous model to determine crude oil salt content, their model was tested over 63 data points from literature, which exposed satisfactory accuracy thanks to high R2 value of 0.9999. Tatar et al. [71] investigated the reservoir brine properties using RBF-NN. The results for density, enthalpy and vapor pressure were comparatively convincing with respect to low corresponding RMSE of 0.270810, 0.455726, and 1.264687, respectively. In a similar attempt, Tatar et al. [72] implemented MLP and GA-RBF models to determine reservoir formation water density. Their models exposed high accuracy since the estimations were in good agreement with experimental data regarding low RMSE of 3.27E-05.
Based on the convincing background of incorporating least square support vector machine and multilayer perceptron neural network to resolve an extensive range of engineering problems, we are pursuing ongoing development and application of LS-SVM and MLP-NN for modeling of brine density of different salts. Therefore, the objective of this study is to develop robust soft computing based models for accurate determination of the density of the brines of different salts for a wide range of concentrations. Underlying the contribution of the article, our developed LS-SVM and MLP-NN models cover a broad range of input flow data including 1868 data sets. Worth noting that the input data cover both natural and synthetic brine densities, which are gathered for the first time.
Indeed, the superior high accuracy in determining density of the brines of different salts is provided implementing the proposed LSSVM and MLP-NN models, which reveals that the aforesaid models would be great assets for science and engineering activities in this domain. The remainder of this article is organized as following; section 3 appertains to background and development of each model. Afterwards, the result of proposed models will be presented in section 4 and both models will be compared with each other. At last, section 5 brings forward a conclusion of the article.
Data acquisition
In order to develop a reliable model it is essential to incorporate valid and authentic data, which covers a wide range of variables [45,73-75]. A set of 1868 data point are utilized in this study, which is gathered from literature [1,24]. The density of pure brines of CaCl2, MgCl2, KI, NaCl, KCl, AlCl3, SrCl2, Na2SO4, and NaHCO3 as well as their different combinations with different salt concentration are investigated in this study. Salt concentration of the samples spans in the range of 0.359-6 mol/kg. The details of the input and output parameters are listed in Table 1.
| Input parameter | Minimum | Maximum | Average | Standard Deviation |
|---|---|---|---|---|
| CaCl2 (mole fraction of salt) | 0 | 1 | 0.113892 | 0.305974 |
| MgCl2(mole fraction of salt) | 0 | 1 | 0.111973 | 0.311183 |
| KI (mole fraction of salt) | 0 | 1 | 0.105996 | 0.307915 |
| NaCl (mole fraction of salt) | 0 | 1 | 0.274283 | 0.413956 |
| KCl (mole fraction of salt) | 0 | 1 | 0.121051 | 0.298603 |
| AlCl3 (mole fraction of salt) | 0 | 1 | 0.034261 | 0.181948 |
| SrCl2 (mole fraction of salt) | 0 | 1 | 0.101313 | 0.3016 |
| Na2SO4 (mole fraction of salt) | 0 | 1 | 0.069138 | 0.250543 |
| NaHCO3 (mole fraction of salt) | 0 | 1 | 0.068126 | 0.25071 |
| Salt Concentration (mol/kg) | 0.359 | 6 | 2.232862 | 1.63979 |
| T (k) | 283.15 | 473.02 | 379.5151 | 57.82789 |
| p (Mpa) | 0.9 | 68.6 | 35.40075 | 22.17534 |
| ρ (kg/m3) | 891.65 | 1406.89 | 1098.936 | 100.0464 |
Table 1: Statistical values of the input and target data.
Backgrounds of modeling
Artificial neural networks are algorithms capable of learning from experience, improving their performance and adapting themselves to the changes in the environment [76]. ANNs have been used for monitoring, controlling, classification, and simulation of activated sludge processes. ANNs can provide numerous benefits such as ability to process a large amount of data and generalize the results, require much less statistical training process, able to diagnose nonlinear relationships between dependent and independent parameters implicitly as well as capable of diagnosing all possible interactions between predictor parameters.
On the other hand, the “black box” nature of ANNs, the great computational stress, susceptibility to over-fitting, and the empirical nature of model generation are the most evident disadvantages of ANNs [44,77]. The two implemented models are described further below.
The support vector machines: The support vector machine (SVM) is a supervised learning technique from the field of machine learning with capability of both classification and regression analysis [78-81]. On the other side, the necessity to resolve a large-scale quadratic programming problem is one of the main defects of the SVM [82]. To deal with this challenge, a new technique so-called Least-Squares SVM (LS-SVM) is presented, which is a modification of the traditional SVM. This technique solves linear equations (linear programming) rather than quadratic programming problems to attenuate the complexity of optimization process [83-85]. Considering the problem of approximating a given dataset 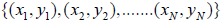 with a nonlinear function:
with a nonlinear function:
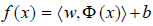 (1)
(1)
Where 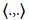 represent dot product; Φ(x) represents the nonlinear function that applies linear regression; b and w are bias terms and weight vector, respectively. In LS-SVM for function prediction, the optimization problem is formulated as [82,86]:
represent dot product; Φ(x) represents the nonlinear function that applies linear regression; b and w are bias terms and weight vector, respectively. In LS-SVM for function prediction, the optimization problem is formulated as [82,86]:
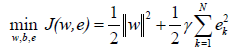 (2)
(2)
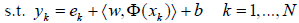 (3)
(3)
where, ek∈R are error variables; and γ ≥0 is a regularization constant. To solve this optimization problem, Lagrange function is established as [82,86]:
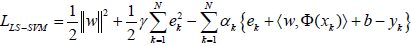 (4)
(4)
where, αkR are Lagrange multipliers. The solution of Eq. (4) can be determined by partially differentiating with respect to w, b, ek and αk [82,86]:
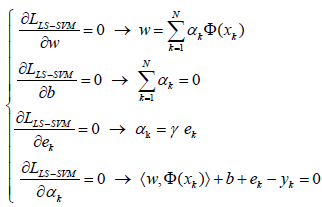 (5)
(5)
By defining 1v = [1;…1], Y = [y1;…;yN], α = [α1;…;αN] and excluding w and e, the following linear equations are obtained [82]:
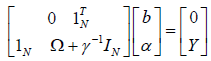 (6)
(6)
where, IN refers to an N×N identity matrix and Ω is the kernel matrix that is introduced as [82]:
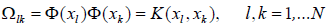 (7)
(7)
There are several kernel functions including linear, spline, polynomial, and radial basis function [87,88]. On the side, radial basis function, a Gaussian function, and polynomial function are the most widespread functions.
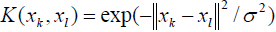 (8)
(8)
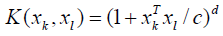 (9)
(9)
where, σ denotes the width of the RBF, which controls the regression capability and d is the polynomial degree.
Multilayer perceptron networks: Multilayer Perceptron Neural Networks (MLP-NNs) consist of three different kind of layers, namely, input layer, hidden layer(s), and output layer (Figure 1). A single MLP may have one or more hidden layer. Each layer comprises some neurons accordingly. The number of neurons in the input and output layers are attributed to the number of input and output data, respectively. The number of hidden layers as well as included neurons in them is optional and can be specified either intelligently or by trial and error to gain the most efficient performance. Minimum Square Error (MSE) demonstrates the performance of the presented network. In such networks, the error is back-propagated through the network and the weights and biases are optimized through some iteration called epochs. The number of epochs should be determined in a manner that the network neither undertrain nor overtrain. In the former, the network does not have sufficient time to complete the learning process. In the latter, the network does not learn but memorizes. This leads to poor performance of network in estimation of test data set. Figure 1 demonstrates a general form of a fully connected multilayer perceptron with two hidden layers.
Figure 1: Structure of a fully connected multilayer perceptron with two hidden layers [90].
There are two different types of signals in MLP network, namely, function signal and error signal. In each node that function signal passes, it is calculated as a function of the inputs values and their corresponding weights and biases. This signal is also called input signal. No computational task is performed in input neurons. In following layers, the activation levels are calculated in each neuron and the results are propagated through the next layers until reaching the output layer. The output of the network is specified in the output layer's neuron(s). Afterwards, this value is compared with the target value and error is calculated. Because the essence of the supervised learning paradigm, error is back-propagated through the network to regulate weights and biases. Here, the other type of signal, namely, error signal is implemented. This signal propagates backward from the output neurons into the network. Figure 2 indicates a portion of the MLP network demonstrating function and error signals [89].
Hidden layer neurons take a significant part in performance of the MLP as they behave as feature detectors. During training process, hidden neurons start to reveal the features of dedicated data for training. This is accomplished by nonlinear transformation of the input data to feature space. In the new space, it is may be easier to separate data from each other for classification. Formation of feature space makes the difference between multilayer perceptron and Rosenblatt perceptron. Each neuron uses an activation function. Sigmoid functions, which are "S" shaped graph, are the most frequent type of activation functions. Further details about Sigmoid functions is available in literature [90].
Designing LS-SVM and MLP models representing density of brines
The first step to start the simulation is data normalization. All the data points including input and output parameters were normalized between -1 and 1 using the following formula:
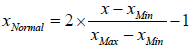 (10)
(10)
At the next step, 80% of the total data were randomly allocated for training and the rest for testing the developed networks. This division is such that there is no local accumulation of train or test data points. Matlab® 2014a was utilized to implement the MLP-NN and LS-SVM codes.
Development of LS-SVM: In order to prevent overfitting problems, the data set was separated into two subdata sets. To this end, 80% and 20% of the main data set was randomly selected for the training set and test set, respectively.
During the computation, the extensively implemented kernel function, i.e., radial basis function (RBF), has been utilized. It has the general form as following [63,64,91]:
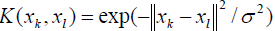 (11)
(11)
in which, σ is a decision parameter that is determined during the optimization calculations [84].
The Mean Square Error (MSE) between the developed model results and corresponding experimental data reported in the literature, as defined by equation (12), was considered as objective function during model computation [92,93].
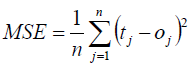 (12)
(12)
in which t and o are target value and estimated value, respectively; and n is number of the data points.
Development of MLP-NN: Cybenko [94] stated that it is mathematically proved that every function can be estimated adequately by an MLP-NN with only one hidden layer. Therefore, only MLP-NNs with only one hidden layer are investigated in this study. Different MLP-NNs structures with 4-25 neurons in the hidden layer were examined and finally it was proved that the MLP-NN with 24 neurons in the hidden layer leads to the best prediction of brine density. The MSE of the examined neural networks is shown in Figure 3.
Accuracy of the proposed model and validation
Both graphical and statistical methods are utilized to validate and show the accuracy of the proposed models. Four different statistical parameters including correlation factor (R2), Average Absolute Relative Deviation (AARD), Standard Deviation (STD), and Root Mean Squared Error (RMSE) are employed (Equations (13)-(16)) to investigate the accuracy of the proposed models. The formulation of these parameters is as follows:
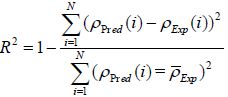 . (13)
. (13)
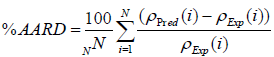 (14)
(14)
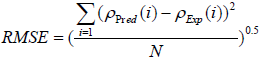 (15)
(15)
The LS-SVM has two tuning parameters called, γ and σ2. Utilizing simulated annealing optimization algorithm, the optimal values for the mentioned values were determined to be 3630241399 and 7.58, respectively.
The statistical parameters obtained from the developed models are demonstrated in Table 2. The statistical parameters are including R2, AARD, STD, and RMSE. As it can be seen, the statistical parameters are calculated for both train and test data sets. With regard to high values of correlation factor for MLP-NN and LS-SVM models, which are 0.999999 and 1.000000, respectively, both developed MLPNN and LS-SVM models enjoy high level of accuracy in predicting experimental data. Furthermore, low values of AARD, STD and RMSE for proposed MLP-NN model which are 0.006893, 0.000115 and 0.117512, respectively, validate the great authenticity of the MLP-NN model. Moreover, the low values of AARD, STD and RMSE obtained from the proposed LS-SVM models which are 0.003657, 5.11E-05 and 0.054512, respectively well demonstrate that the model estimations are in great accordance with experimental data points.
| R^2 | AARD | STD | RMSE | N | ||
|---|---|---|---|---|---|---|
| MLP-NN | Train Data | 0.999999 | 0.006483 | 0.000101 | 0.104272 | 1494 |
| Test Data | 0.999998 | 0.008532 | 0.000159 | 0.159809 | 374 | |
| All Data | 0.999999 | 0.006893 | 0.000115 | 0.117512 | 1868 | |
| LS-SVM | Train Data | 1.000000 | 0.003246 | 4.46E-05 | 0.047559 | 1494 |
| Test Data | 0.999999 | 0.0053 | 7.15E-05 | 0.076201 | 374 | |
| All Data | 1.000000 | 0.003657 | 5.11E-05 | 0.054512 | 1868 |
Table 2: Statistical parameters of the proposed models.
Accuracy of the developed models is further investigated by means of graphical analysis methods such as cross plot, relative deviation, and error distribution. Cross plots indicate the degree of validation, whereas error distribution explains if the developed models have an error trend.
Figures 4-7 are indicative of comparison between MLP-NN and LS-SVM models estimated/represented brine density and target (experimental) values for both train and test data sets.
Figures 4(a) and 4(b) display a scatter plot of experimental brine density versus developed MLP-NN and LS-SVM models estimation, respectively. These plots are for both train and test data sets. At it is displayed, presence of almost all data points on the bisector of the first quadrant leads us to a conclusion that a close agreement is obtained between the predictions of both MLP-NN and LS-SVM models and the experimental data points for both train and test data sets.
The degree of correspondence between experimental data points and MLP-NN and LS-SVM models estimated values is further demonstrated in Figures 5(a) and 5(b), respectively. Figure 5 displays the relative deviations of the proposed models predictions versus experimental data points for both train and test data sets. According to the Figure 5, the predicted brine densities are in a desired agreement with target values since the distribution of relative deviation is close to the horizontal line and almost coincides that. For the sake of better visual comparison, the estimated and target values are displayed simultaneously versus the data point number (i.e., data index) for both MLP-NN and LS-SVM models in Figures 6(a) and 6(b), respectively. It goes without saying that coincidence of the experimental and predicted values signifies the accuracy of both MLP-NN and LS-SVM models. In order to shed more light on the reliability of developed models, the error distribution plot is demonstrated for both proposed models in Figure 7. For both models, as it is displayed, the error distribution is completely symmetric around the center of 0. To round it off, RMSE bar plot of both MLP-NN and LS-SVM models is illustrated for train, test, and all data sets in Figure 8. The result explains that the LS-SVM model slightly outperforms MLP-NN model, however, both models enjoy great accuracy with respect to low values of RMSE (0.054512 and 0.117512, respectively) and other statistical parameters including R2, AARD and STD.
Various scopes of industry face a serious challenge for precise determining of brine density. These scopes are more around fluid inclusion surveys, CO2 sequestration, studies of fluid-rock interaction, drilling industry and Enhanced Oil Recovery (EOR). In spite of recent breakthrough in determining brine properties including brine density, a swift reliable model is required for an accurate determination of brine density. Hereupon, two soft computing models named, LS-SVM and MLP-NN have been proposed in this paper to address this need. These models cover both natural and synthetic brines as well as an extensive range of input parameters including temperature, pressure, and concentration.
The reliability of designed models was verified in favor of employing statistical parameters. Indeed, the LS-SVM and MLP-NN revealed R2 of 1.000000 and 0.999999, AARD of 0.003657 and 0.006893, STD of 5.11E-05 and 0.000115 and RMSE of 0.054512 and 0.117512, respectively. Hereupon, it can be concluded that developed models are reliable enough to predict brine density, which correspondingly they can be implemented to assist delicate industrial designations.