Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
ISSN: 2157-7544
Research Article - (2014) Volume 5, Issue 2
ndividual distribution constants ( K D,A ) of picrate ion (Pic − ) into nitrobenzene (NB) were determined at 298 K and given values of ionic strength, together with the determination of an extraction constant ( K ex ) for the extraction of alkaline-earth metal picrates, MPic 2 , by 18-crown-6 ether (18C6) and benzo-18C6 (B18C6). Here, K D,A and K ex were defined as [A − ] NB /[A − ] and [MLA 2 ] NB /[M 2+ ][L] NB [A − ] 2 , respectively: A − shows Pic − , L does either 18C6 or B18C6 and the subscript “NB” refers to the NB phase. Interfacial potential differences (∆ φ eq in a V unit) at extraction equilibria were evaluated from differences between the experimental log K D,Pic and its standardized values (log KD , Pic S ) which have been determined by electrochemical measurements at a water/NB interface. By a combination with the K ex values, other extraction constants, K ex± =[MLPic + ] NB [Pic − ] NB /[M 2+ ][L] NB [Pic − ] 2 , were also determined. Electrochemically- standardized log K ex± values, log K ex± S ones, were calculated from the relation of log K ex± = (∆ φ eq /0.05916) + log K ex± S at 298 K. Using the log K ex± S values, their correlation with the log K ex± ones was discussed. Additionally, ion-pair forma- tion constants ( K 1,NB & K 2,NB ) for the stepwise reactions of ML 2+ with Pic − in the NB phase were evaluated from K ex , K ex± and another constant ( K ex2± ) reported before at ∆ φ eq = 0. Here, K 2,NB was evaluated from K ex / K ex± and K 1,NB is defined as [MLPic + ] NB /[ML 2+ ] NB [Pic − ] NB , which was evaluated from the relation of K 1,NB = K ex± / K ex2± . Moreover, reproductions of the electrochemically-standardized K ex± and K ex2± values were tried, using the ∆ φ eq values and relations between K ex± or K ex2± and component equilibrium constants constituting their extraction ones. Consequently, a functional expres - sion of K ex± with ∆ φ eq was extended into the MPic 2 -L extraction systems, in addition to the AgPic-L extraction ones reported previously
Keywords: Interfacial potential differences; Individual distribution constants of ions; Extraction into nitrobenzene; Alkaline-earth metal picrates; 18-Crown-6 ether derivatives
Recently one of the authors has reported an expression by an interfacial potential difference (Δφeq) of an extraction constant on silver picrate extraction with crown ethers (L) into 1,2-dichloroethane (DCE) or dichloromethane (DCM) [1]. In this study, its extraction constant has been defined as [AgL+]o[Pic−]o/([Ag+][L]o[Pic−]), in addition to the well-known definition of Kex = [AgL+Pic−]o/([Ag+][L]o[Pic−]), where the subscript “o” and Pic− denote an organic (o) phase, such as DCE and DCM, and picrate ion, respectively. An introduction of Δφeq in extraction experiments also gave an answer for a problem of the deviation between the electrochemically-determined KD,A values and extraction-experimentally-determined values [1,2]. Here, the symbol KD,A refers to an individual distribution constant (= [A−]o/[A−]) of A− into the o phase. Similar problems have been observed in the extraction of divalent metal salts, such as CdPic2, PbPic2 and CaPic2, by L into various diluents [3-5].
In the present paper, we determined at 298 K the KD,Pic values for the extraction of alkaline-earth metal picrates (MPic2: M = Ca, Sr, Ba) by 18-crown-6 ether (18C6) or benzo-18C6 (B18C6) into nitrobenzene (NB) which shows the higher polarity. Then, the Δφeq values were evaluated from differences between the KD,Pic values electrochemicallydetermined and those determined by the present extractionexperiments. Here, the electrochemically-determined constant was expressed as KD,PicS, showing the equilibrium constant standardized at Δφeq = 0 V [1,6,7]. Moreover, the functional expressions of Kex±, Kex2± and Kex by Δφeq were examined; the symbols, Kex±, Kex2± and Kex, refer to [MLA+]o[A−]o/([M2+][L]o[A−]2), [ML2+]o[A−]o 2/([M2+][L]o[A−]2) and [MLA2]o/([M2+][L]o[A−]2), respectively [3,4,8]. On the basis of the above values determined, the MIIPic2 extraction system with L into NB was characterized.
Derivation of a potential difference at the water/o interface
Using properties of electrochemical potentials 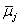 [9,10], we had reported relations between Δφeq and the constants expressing overall extraction equilibria, such as M+ + Lo + A−
[9,10], we had reported relations between Δφeq and the constants expressing overall extraction equilibria, such as M+ + Lo + A−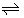 MLAo and M+ + Lo+ A−
MLAo and M+ + Lo+ A−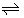 ML+o + A−o [1]. The same handling [1,11] was applied for the present extraction equilibria. For example, the authors will apply it to the process:
ML+o + A−o [1]. The same handling [1,11] was applied for the present extraction equilibria. For example, the authors will apply it to the process:
M2+ + Lo + 2A−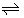 MLA+o+ A−o. (1)
MLA+o+ A−o. (1)
This process was expressed by 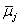 as
as
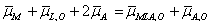 (2)
(2)
μM 0 + RTln aM + 2FφM + μL,o 0 + RTln aL,o + 2(μA 0 + RTln aA − FφA)
= μMLA,o 0 + RTln aMLA,o + FφMLA,o + μA,o 0 + RTln aA,o− FφA,o. (2a)
Rearranging this equation for the Kex± definition, then we obtained
RTln Kex± 0 + μMLA,o 0 + μA,o 0 − μM 0 − μL,o 0 − 2μA0
= F{(2φM − φMLA,o) − (2φA − φA,o)}.
Therefore, the following equations were derived:
Δφeq = Δφex± 0 + (2.3RT/F)log Kex± 0 (3)
with Δφeq = (2φM − φMLA,o) − (2φA − φA,o), Δφex± 0 = (μMLA,o 0 + μA,o 0 − μM 0 − μL,o 0 − 2μA0)/F and Kex± 0 = aMLA,o aA,o/{aMaL,o(aA)2}. Here,φj,α and aj,α denote an inner potential for species j in the phase α (= o) and an activity of j in the α phase, respectively; the symbols without α mean those to the water (w) phase, although there is an exception to this rule. From Equation (3), the interfacial potential difference Δφeq at an equilibrium was defined [1,11]; in principle, Δφeq has been defined as φ(w phase) − φ(o phase). Then, rearranging Equation (3) in a molar concentration unit, we immediately obtain
Δφeq = Δφex± 0′ + (2.3RT/F)log Kex± (3a)
with Δφex± 0 ′ = Δφex± 0 + (2.3RT/F)log [yMLA,oyA,o/{yM(yA)2}] and Kex± = [MLA+]o[A−]o/([M2+][L]o[A−]2). Here, yj,α refers to an activity coefficient of the ionic species j {= MLA(I), A(−I), M(II)} in the α phase; the symbol y without α shows the coefficient for the w phase; Δφk 0′ means a standard formal potential. Similarly, equilibrium constants of other processes were expressed as functions of potential differences. These results are listed in Table 1. The condition of Δφeq = 0 V was applied for some processes from their properties: namely, Δφeq essentially becomes zero, when all species relevant to the inner potentials are present in a single phase [1,9].
| Process | Symbol | Relationa |
|---|---|---|
| Overall | ||
M2+ + Lo + 2A- 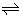 MLA2,o MLA2,o |
Kex | Log Kex = -2fΔfex0¢ |
M2+ + Lo + 2A- 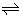 MLA+o + A-o MLA+o + A-o |
Kex± | Log Kex± = f(Δfeq - Δfex±0¢) |
M2+ + Lo + 2A- 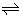 ML2+o + 2A-o ML2+o + 2A-o |
Kex2± | Log Kex2± = 2f(Δfeq - Δfex2±0¢) |
| Component | ||
M2+ 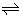 M2+o M2+o |
KD,M | Log KD,M = 2f(Δfeq - ΔfM0¢) |
ML2+ 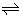 ML2+o ML2+o |
KD,ML | Log KD,ML = 2f(Δfeq - ΔfML0¢) |
A- 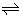 A-o A-o |
KD,A | Log KD,A = -f(Δfeq - ΔfA0¢) |
M2+o + Lo 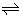 ML2+o ML2+o |
KML.org | Log KML.org = -2fΔfML.org0¢ |
M2+ + 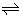 LML2+ LML2+ |
KML | Log KML = -2fΔfML.w0¢b |
| LLo | KD,L | Log KD,L= -fΔfL0¢ |
ML2+o + A-o 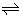 MLA+o MLA+o |
K1,org | Log K1,org = -fΔf1,org0¢ |
MLA+o + A-o 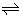 MLA2,o MLA2,o |
K2,org | Log K2,org = -fΔf2,org0¢ |
ML2+o + 2A-o 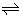 MLA2,o MLA2,o |
bip,orgc | Log bip,org = -2fΔfip,org0¢ |
af = F/2.3RT. Hence, 1/f = 0.05916 V at 298 K. bΔφML.w 0′ shows a standard formal potential for the ML2+ formation in the w phase. cβip,org = K1,org K2,org. Accordingly, the relation of 2Δφip,org 0′ = Δφ1,org 0′ + Δφ2,org 0′ holds
Table 1: Relations between the potential differences, Δφeq, Δφk 0′ or Δφj0′, and Log Kk values in an extraction system.
Using thermodynamic cycles and the various equilibrium constants in Table 1, we can express the overall extraction processes [1]. Thereby, it becomes possible that we express the overall extraction constants as functions of some formal potentials with Δφeq. As an example, Kex2± (see Introduction for its definition) is expressed as KD,M(KD,A)2KML,org. Taking logarithms of both sides in this equation and rearranging it based on the corresponding relations in Table 1, we easily obtain
Δφex2± 0′ = ΔφM 0′ − ΔφA 0′ + ΔφML,org 0′ + Δφeq (4)
from Δφeq − Δφex2± 0′ = (Δφeq − ΔφM 0′) − (Δφeq − ΔφA 0′) − ΔφML,org 0′. The same was true of Kex and Kex±, where the condition of Δφeq = 0 V was satisfied for Kex, since all species relevant to the inner potentials were present in the single phase [1,9]. Table 2 summarizes these results. According to the previous paper [1], when the log KD,A values are determined experimentally and the ΔφA 0′ ones are available, we immediately can calculate the Δφeq values from the relation in Table 1.
| Overall process & Its cyclea | Relationb |
|---|---|
M2+ + Lo + 2A- 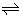 MLA2,o Kex = KD,M(KD,A)2KML,org bip,org MLA2,o Kex = KD,M(KD,A)2KML,org bip,org |
Dfex0¢ = DfM0¢ - DfA0¢ + DfML,org0¢ + Dfip,org0¢ |
M2+ + Lo + 2A- 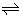 MLA+o + A-o (a) Kex± = KD,M(KD,A)2KML,org K1,org (b) Kex± = KML KD,ML K1,org(KD,A)2/KD,L MLA+o + A-o (a) Kex± = KD,M(KD,A)2KML,org K1,org (b) Kex± = KML KD,ML K1,org(KD,A)2/KD,L |
(a) Dfex±0¢ = 2DfM0¢ - 2DfA0¢ + 2DfML,org0¢ + Df1,org00¢ + Dfeq (b) Dfex±0¢ = 2DfML,w0¢ + 2DfML0¢ + Df1,org00¢ - 2DfA0¢ - DfL0¢ + Dfeq |
M2+ + Lo + 2A- 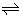 ML2+o + 2A-o Kex2± = KD,M(KD,A)2KML,org ML2+o + 2A-o Kex2± = KD,M(KD,A)2KML,org |
Dfex2±0¢ = DfM0¢ - DfA0¢ + DfML,org0¢ + Dfeq |
aA thermodynamic cycle of an extraction constant expressed by the component equilibrium constants. bΔφip,org 0′ = (Δφ1,org 0′ + Δφ2,org 0′)/2
Table 2: Some examples on relations between the Δφk 0′ values and the potential differences based on component equilibrium constants.
For an analytical handling of extraction processes
The extraction-constant parameter, Kex mix, has been employed for the determination of KD,A and Kex [3-5]:
log Kex mix = log {([MLA2]o + [MLA+]o)/([M2+][L]o[A−]2)}
= log {Kex + KD,A/([M2+][L]o[A−])} (5)
under the condition of [A−]o ≈ [MLA+]o (>> 2[M2+]o + 2[ML2+]o). A regression analysis to the plot of log Kex mix versus −log ([M2+][L]o[A−]) yielded the KD,A and Kex values [3-5]. Equation (5) can be also rearranged as
log Kex mix = log {Kex + (Kex±/[M2+][L]o)1/2[A−]−1}. (5a)
Then, this equation makes it possible that one obtains the Kex± value from the plot of log Kex mix versus −log {([M2+][L]o)1/2[A−]}. In this study, the regression analyses with Equation (5a) were performed at a fixed condition of the Kex value which was determined in terms of the analysis of Equation (5) and accordingly the thus-obtained Kex± value was checked by calculating it from each experimental point (Table 3).
| L | M | log KD,A | log Kex ()a | log Kex± | log Kn,NB ()b | |
|---|---|---|---|---|---|---|
| n = 1 | 2 | |||||
| 18C6 | Ca | -1.43 ± 0.03 | 9.82 ± 0.02 (5.3×10-3) | 5.44 ± 0.07 5.43 ± 0.18c | 5.9 [4.7]d | 4.38 ± 0.08 (8.9×10-4) |
| Sr | -0.98 ± 0.07 | 11.44 ± 0.03 (3.1×10-3) | 6.92 ± 0.12 6.91± 0.13c | 5.3 [4.6]d | 4.52±0.12 (4.8×10-4) | |
| Ba | -0.69 ± 0.04 | 10.75 ± 0.08 (4.5×10-3) | 7.35 ± 0.11 7.44 ± 0.33c | 4.9 [3.4]d | 3.41 ± 0.14 (5.9×10-4) | |
| B18C6 | Ca | -1.92 ± 0.04 | 7.35 ± 0.08 (3.6×10-3) | 2.71 ± 0.10 2.80 ± 0.29c | 5.0 [5.5]d | 4.64 ± 0.13 (6.9×10-4) |
| Sr | -1.34 ± 0.04 | 9.41 ± 0.02 (4.0×10-3) | 4.34 ± 0.08 4.33 ± 0.13c | 4.7 [4.6]d | 5.07 ± 0.08 (2.3×10-4) | |
| Ba | -1.17 ± 0.02 | 9.51 ± 0.02 (4.7×10-3) | 5.01 ± 0.11 5.08 ± 0.42c | 4.1 [4.2]d | 4.50 ± 0.11 (2.1×10-4) | |
aAverage values of I in the w phase. bAverage values of INB in the NB phase. cLogarithms of average values calculated from each values of Kex± and their propagation errors simultaneously-calculated. dNumber, h, of water molecules coextracted with ML2+ into the NB phase. See ref. [17]
Table 3: Fundamental equilibrium constants for the extraction of alkaline-earth metal picrates by L into nitrobenzene at 298 K.
Evaluation of stepwise ion-pair formation constants for MLA2 in the o phase
Stepwise ion-pair formation constants for MLA2 in the watersaturated o phase for given Iorg,av values were evaluated from the following relations.
K1,org = [MLA+]o/[ML2+]o[A−]o = Kex±/Kex2± (6)
K2,org = [MLA2]o/[MLA+]o[A−]o = Kex/Kex± (7)
Here, the symbol, Iorg,av, was defined as (ΣIorg)/N with a number (N ) of run and ionic strength (Iorg) for the o phase. Table 3 lists the five equilibrium constants determined with the above procedures. The Kex2± S values which were available from references [8] were actually used as Kex2± in the K1,NB-calculation with Equation (6). Strictly speaking, there is a difference between actual contents calculated from Equations (6) and (7). See Appendix for this details.
Chemicals
Purities of commercial Ca(NO3)2•4H2O {Kanto Chemical Co. (Kanto), guaranteed reagent (GR)}, Sr(NO3)2 (Kanto, GR) and Ba(NO3)2 {Wako Pure Chemical Industries (Wako), GR} were checked by a chelatometric titration with disodium salt of EDTA. Also, a purity of commercially-available picric acid, HPic, with amount of 10-15%(w/w) water (Wako, GR) was checked by an acid-base titration [1,5]. Commercial crown ethers, 18C6 (99%, Acros) and B18C6 (98%, Aldrich), were dried at room temperature for >20 h under a reduced pressure. Their purities were checked by measurements of the melting points: 39.7-40.1 or 37.2-39.9 °C for 18C6; 42.3-42.8 for B18C6. Additionally, their water contents were determined by a Karl-Fischer titration: 0.4628%(w/w) for 18C6 and 0.4107 for B18C6. Nitrobenzene (Kanto, GR) was washed three-times with water and then kept at a water-saturated condition. Other chemicals were of GR grades and used without further purifications. A tap water was distilled once with a still of the stainless steel and then purified by passing through the Autopure system (type WT101 UV, Yamato/Millipore). Thus purified water was employed for the present work.
Extraction procedures
Alkaline-earth metal nitrates M(NO3)2, HPic and L were mixed with 0.002 mol dm−3 HNO3 in a stoppered glass-tube of about 30cm3 and then the same volume of NB was added in its solution. Their total concentrations were [Ca(NO3)2]t = 0.0012 mol dm−3, [HPic]t = 0.0024 and [18C6]t = (0.70-7.0) × 10−4; [Sr(NO3)2]t = 6.8 × 10−4, [HPic]t = 0.0014 and [18C6]t = (0.86-6.4) × 10−4; [Ba(NO3)2]t = 8.8 × 10−4, [HPic]t = 0.0018 and [18C6]t = (0.071-2.6) × 10−3 and [Ca(NO3)2]t = 8.0 × 10−4, [HPic]t = 1.6 × 10−3 and [B18C6]t = (0.080-2.4) × 10−3; [Sr(NO3)2]t = 4.1 × 10−4, [HPic]t = 8.2 × 10−4 and [B18C6]t = (0.082-2.5) × 10−3; [Ba(NO3)2] t = 3.5 × 10−4, [HPic]t = 7.1 × 10−4 and [B18C6]t = (0.032-2.0) × 10−3. The thus-prepared glass tube was shaken for 1 minute by hand and was agitated at 298 ± 0.2 K for 2 h in a water bath (Iwaki, type WTE-24) equipped with a driver unit (Iwaki, SHK driver) and a thermoregulator (Iwaki, type CTR-100). After this operation, its mixture was centrifuged with a Kokusan centrifuge (type 7163-4.8.20) for 7 minutes.
A portion of the separated NB phase was transferred into another stoppered glass-tube and then 0.1 mol dm3 HNO3 was added in this tube. By shaking the tube, all M(II) species in the NB phase were bacKextracted into the HNO3 solution. If necessary, the operation for this back extraction was repeated. An amount of all the M(II) species in the aqueous HNO3 solution was determined by a Hitachi polarized Zeeman atomic absorption spectrophotometer (type Z-6100) with a hollow cathode lamp of Ca (type 10-020, Mito-rika Co. under the license of Hitachi, Ltd.; measured wavelength: 422.7 nm) or Sr (type 10-038, Mito-rika Co.; 460.7 nm). A calibration-curve method was employed for the determination of the M(II) concentration by AAS. For the Ba(II) determination, a >0.1 mol dm−3 NaOH solution was added in the back-extracted solution with Pic− and then its Ba(II) solution was measured at 355 nm based on the Pic− absorption and 298 K by a spectrophotometer (Hitachi, type U-2001). The Ba(II) concentration was determined with a calibration curve which had been prepared at 355 nm. On the other hand, the pH value in the separated w phase was measured at 298 K with the same electrode and pH/ion meter [1,4,5].
Determination of Kex mix
We used here the same extraction model as that [5] for subanalysis described previously. Its component equilibria are 1) M2+ + A- 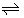 MA+ [12], 2)* A-
MA+ [12], 2)* A- 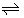 A- o, 3)* M2+
A- o, 3)* M2+ 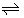 M2+o, 4) MLA+ o + A- o
M2+o, 4) MLA+ o + A- o 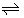 MLA2,o, 5) ML2+
MLA2,o, 5) ML2+ 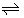 ML2+o, 6)* L
ML2+o, 6)* L 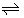 Lo, 7)* M2+ + L
Lo, 7)* M2+ + L 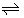 ML2+, 8)* M2+o + Lo
ML2+, 8)* M2+o + Lo 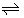 ML2+ o, 9)* H+ + A-
ML2+ o, 9)* H+ + A- 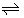 HA [4], 10)* HA
HA [4], 10)* HA 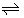 HAo [4], 11)* HAo
HAo [4], 11)* HAo 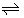 H+o + A- o [13], 12)* H+
H+o + A- o [13], 12)* H+ 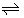 H+ o [6], 13)* X−
H+ o [6], 13)* X− 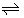 X- o [11] and 14)* H+ o + X-o
X- o [11] and 14)* H+ o + X-o 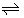 HXo [11], where the symbol HX shows a strong acid, such as HNO3 and HCl, in water. In particular, the two reactions, 7) and 8), indirectly yielded the process 5). Also, the parentheses with the asterisks show that their equilibrium constants at 298 K have been already determined by several methods (see below for some values).
HXo [11], where the symbol HX shows a strong acid, such as HNO3 and HCl, in water. In particular, the two reactions, 7) and 8), indirectly yielded the process 5). Also, the parentheses with the asterisks show that their equilibrium constants at 298 K have been already determined by several methods (see below for some values).
The equilibrium constants for the reactions 1) and 9) were estimated taking account of the ionic strength, I, for the w phases in a successive approximation [3,5]. Here, the formation constants (KMA) for MA+ = MPic+ (M = Sr, Ba) in the w phase were determined by the same method as that [4] reported before: as the log KMPic values at 298 K and I → 0 mol dm−3, 2.18 for M = Sr and 2.08 for Ba were obtained. While the KCaPic value was estimated with the value available from reference [12].
The procedure for the calculation of Kexmix values by the successive approximation was essentially the same as that [3] described previously (see the theoretical section). Plots of log (Dexpl./[Pic−]2) versus log [L]NB gave a straight line with a slope of 0.56 and an intercept of 7.9 for the CaPic2-18C6 system, 0.91 and 11.1 (≈ log Kex) for SrPic2-18C6, 0.62 and 9.4 for BaPic2-18C6, 0.38 and 5.9 for CaPic2-B18C6, 0.65 and 8.5 for SrPic2-B18C6 and 0.44 and 7.9 for BaPic2-B18C6. Here, the distribution ratio Dexpl. is defined as [AAS-analyzed M(II)]NB/{[M(NO3)2]t − [AASanalyzed M(II)]NB} and the intercept corresponds to the log Kex value only when the slope is about unity [3-5]. Except for the SrPic2-18C6 system, the compositions of M(II):L:Pic(−I) were assumed to be 1:1:2 in the determination of KD,Pic, Kex and Kex± [3-5]. The slope’s values less than unity indicate dissociations of MLPic2 in the NB phases [4]. Figures 1 and 2 show the plots for the BaPic2-18C6 extraction system based on Equations (5) and (5a), respectively, yielding the KD,Pic, Kex and Kex± values (Table 3). The less correlation coefficient (R) of the plot in Figure 2 may reflect the defect in the sub-analytical extraction model [4,5], that is, the absence of the ion-pair formation for MLPic2 in the w phase. Also, the other extraction systems yielded similar plots, from which we got similarly these three kinds of values (Tables 3).
In the determination of KD,Pic, Kex and Kex± for the BaPic2-L extraction system, it was assumed that a total amount, [Ba(II)]NB,t, of Ba(II) in the NB phase nearly equals the half of that, [Pic−]NB,t, of Pic− in the NB one. This assumption was derived as follows. A charge balance equation for the NB phase was essentially
2[Ba2+]NB + 2[BaL2+]NB + [BaLPic+]NB + [H+]NB = [Pic−]NB + [X−]NB, (8)
where the distribution of BaPic+ into the NB phase was neglected, because its data were not available. When [H+]NB ≈ [X−]NB holds, Equation (8) becomes 2[Ba2+]NB + 2[BaL2+]NB + [BaLPic+]NB ≈ [Pic−]NB. Rearranging this equation and adding 2[BaLPic2]NB in its both sides, we can immediately obtain
[Pic−]NB + 2[BaLPic2]NB = [Pic−]NB,t
≈ 2[Ba2+]NB + 2[BaL2+]NB + [BaLPic+]NB + 2[BaLPic2]NB. (8a)
Hence, when the condition of 2[BaLPic2]NB > [BaLPic+]NB (> 2[BaL2+]NB + 2[Ba2+]NB) holds, the half of the left hand side of Equation (8a) approximately becomes [Ba2+]NB + [BaL2+]NB + [BaLPic+]NB + [BaLPic2]NB, namely [Ba(II)]NB,t. We were able to determine spectrophotometrically the ([Pic−]NB + 2[BaLPic2]NB) value at least by the back extraction experiments.
Tendencies of KD,Pic, Kex, Kex± and Kn,NB at n = 1, 2
As can be seen from Table 3, the log KD,Pic values are different from each other in spite of the same definition. These are in the orders of Ca < Sr < Ba for a given L. Also, the orders are B18C6 < 18C6 for a given M(II). Thus, these KD,Pic orders are influenced by sizes [14,15] of M2+ and L, not cavity sizes of L; molar volumes of L were reported to be 214 cm3 mol−1 for L = 18C6 and 252 for B18C6 [15].
The values of both log Kex and log Kex± were in the orders of Ca < Sr < Ba (Table 3). These tendencies are similar to those for log KD,M S and log KML,NB (see below for these values). Such facts suggest the presence of these equilibrium constants in the thermodynamic cycles (Table 2). Also, two procedures for evaluating the log Kex± values in Table 3 well agreed within calculation errors. These facts support that the regression analyses based on Equation (5a) are essentially valid under the conditions of constant Kex values.
Orders of the log K1,NB values were Ca > Sr > Ba for the both L, when we neglected differences in INB among the extraction systems (see Table 3 for INB). On the other hand, the log K2,NB values were Ca < Sr > Ba. These differences suggest that sizes of M(II) are more-effectively reflected to stability of the 1st-step ion-pair formation than to that of the 2nd-step formation. In other words, these results seem to be due to differences in a size and/or charges, such as the formal and net charges, between ML2+ and MLPic+ as reaction species in NB saturated with water. Also, such effects may be reduced in the more-bulky SrPic2- and BaPic2-B18C6 systems.
As another explanation for the K2,NB orders, it can be considered that the INB values of the Ca(II) system are largest of all the systems. The INB orders were of M = Ca > Sr < Ba for L = 18C6 and Ca > Sr ≥ Ba for B18C6 (Table 3). The highest INB values for the Ca(II) systems may cause the lowest K2,NB values. While their values were less effective for the K1,NB values, because K1,NB is constituted by the concentrations of all the ionic species.
If the 1st-step ion-pair formation is assumed to be
ML2+•hH2ONB + Pic−NB MLPic+•mH2ONB + pH2ONB (9)
with p = h − m, then K1,NB can be expressed as K1,NB′/([H2O]NB)p with K1,NB′ = [MLPic+]NB([H2O]NB)p/[ML2+]NB[Pic−]NB (as an expression without a hydrated H2O). Here, the hydration of Pic− in the NB phase was neglected [16]. From Table 3, the larger the h values [17] are, the larger the K1,NB values become. These facts suggest that the m values are about a constant and thereby the p values are proportional to the h ones. Taking logarithms of the both sides of the equation, K1,NB = K1,NB′/ ([H2O]NB)p, we can immediately obtain the equation, log K1,NB = log K1,NB′ − p × log [H2O]NB. Under the conditions of [H2O]NB (= 0.178 mol dm−3 at 298 K [17,18]) < 1 and p > 0, the equation becomes log K1,NB = log K1,NB′ + 0.750p. Therefore, the log K1,NB values basically increase with an increase in p and consequently can increase with that in h (Table 3). The above results suggest the existence of the reaction (9) with H2O molecules in NB phase, as reported before on the process of M+ + LNB + A- 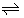 ML+ NB + A- NB [8].
ML+ NB + A- NB [8].
Calculation of the Δφeq values from the experimental log KD,Pic values
Using the relation of log KD,A = −(Δφeq − ΔφA 0)/0.05916 at 298 K (Table 1), we calculated the Δφeq values from the log KD,Pic and ΔφPic0′ones, where the ΔφPic0′value of 3.0 × 10−3 V [6] at the w/NB interface was employed. Thus obtained values are summarized in Table 4. The Δφeq range for the 18C6 system was a little smaller than that for B18C6 one. From a comparison with the log Kex± values in Table 3, the smaller the Δφeq values are, the larger the log Kex± ones become. This trend is similar to that reported previously for the extraction of AgPic by B18C6 and benzo-15-crown-5 ether B15C5 into DCE or DCM [1].
| L | M | Dφeq/Va | log Kex±S | log Kex2±S | ||
|---|---|---|---|---|---|---|
| Foundb | Calcdc | Foundd | Calcde | |||
| 18C6 | Ca | 0.088 | 3.96 | 3.96 | -0.5 | -3.46 |
| Sr | 0.061 | 5.89 | 5.93 | 1.6 | -0.42 | |
| Ba | 0.044 | 6.61 | 6.89 | 2.4 | 1.21 | |
| B18C6 | Ca | 0.12 | 0.75 | 0.78 | -2.3 | -6.20 |
| Sr | 0.082 | 2.95 | 2.99 | -0.4 | -3.14 | |
| Ba | 0.072 | 3.79 | 4.07 | 0.6 | -1.56 | |
aEssentially based on Δφ/V versus Ph4As+BPh4 − electrode. bCalculated from the relation of log Kex± = f(φeq − Δφex± 0′) in Table 1. cCalculated from the relation of Δφex± 0′ = 2(ΔφM 0′ − ΔφA 0′ + ΔφML,org 0′) + Δφ1,org 0′ + Δφeq in Table 2. dCalculated from the thermodynamic cycle, log Kex2± = log KD,M S + 2log KD,Pic S + log KML,NB. See ref. [8]. eCalculated from the relation of Δφex2± 0′ = ΔφM 0′ − ΔφA 0′ + ΔφML,org 0′ + Δφeq in Table 2
Table 4: Δφeq and the log Kex± and log Kex2± values at 298 K standardized by their potentials.
Determination of the log Kex± S and log Kex2± S values
The Δφex± 0 ′ values were evaluated from the Δφeq and log Kex± values (Tables 3&4) using log Kex± = (Δφeq − Δφex± 0′)/0.05916 listed in Table 1. After these evaluations, the log Kex± S values were calculated from the same equation at the condition of Δφeq = 0 V. The same values were evaluated from Δφex 0 ′= 2φM0′ − 2ΔφA0′ + 2ΔφML,org 0′ + Δφ1,org 0′ + Δφeq in Table 2 and then log Kex± S = −Δφex± 0 ′/0.05916. Here, we calculated the ΔφM0′ values from log KD,M S = −11.799 for M = Ca, −11.562 for Sr and −10.818 for Ba [19] and similarly the ΔφML,NB 0′ values from log KML,NB = 11.2 for ML2+ = Ca(18C6)2+, 13.1 for Sr(18C6)2+, 13.4 for Ba(18C6)2+, log KML,NB = 9.43 for Ca(B18C6)2+, 11.1 for Sr(B18C6)2+ and 11.6 for Ba(B18C6)2+ [20]. Also, the Δφ1,NB0′ values were calculated from the relation of log K1,NB = −Δφ1,NB0′/0.05916 (Table 1) and the log K1,NB values in Table 3. Similar evaluations were performed for the log Kex2± S values using the relation among the potentials listed in Table 2.
As can be seen from Table 4, the log Kex± S values calculated from the relation in Table 1 are equal or close to those calculated from that in Table 2. Especially, a little larger deviations for the BaPic2-L systems may be due to the approximation of [Ba(II)]NB,t ≈ [Pic−]NB,t (see Materials and Methods). On the other hand, the log Kex2± S values calculated from the relation in Table 2 are very small, compared to those [8] reported before, although the order in magnitude of the calculated values is the same as that of the reported ones [8]. A correlation between these two orders was expressed by the following equation: log Kex2± S(calcd) = (1.54 ± 0.05)log Kex2± S(found) − (2.62 ± 0.07) at R = 0.998. Also, differences between the log Kex2± S(calcd) and log Kex2± S(found) values
were in the range of 1.2 to 3.9 (Table 4). (i) These differences can be due to experimental errors of data, because estimated fractions, [ML2+]NB/ [ AAS-analyzed M(II)]NB, were in the ranges of 0.0012-0.043% for M = Ca, 0.024-0.33 for Sr and 0.05-3.1 for Ba. That is, these values indicate that the amounts of ML2+ in the NB phases are negligible, compared to those of all species with M(II) in the phases and accordingly the Kex2± evaluations may cause the larger errors. (ii) Or the difference can come from the fact that the original extraction model does not take account of the overall process, M2+ + LNB + 2Pic− 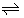 ML2+ NB + 2Pic−NB. While the overall process, M2+ + LNB + 2Pic−
ML2+ NB + 2Pic−NB. While the overall process, M2+ + LNB + 2Pic− 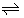 MLPic+ NB + Pic−NB, has been included in the model [3-5] {see Equation (5a)}. However, it is unclear whether the two above facts, (i) and (ii), cause the negative errors of log Kex2 S or not.
MLPic+ NB + Pic−NB, has been included in the model [3-5] {see Equation (5a)}. However, it is unclear whether the two above facts, (i) and (ii), cause the negative errors of log Kex2 S or not.
Figure 3 shows a plot of log Kex± versus log Kex± S(found) for all the MPic2-L systems. Here, the former logarithmic values are listed in Table 3, while the latter values in Table 4. The plot gave a good correlation between both the values: log Kex± = (0.81 ± 0.03)log Kex± S(found) + (2.07 ± 0.13) at R = 0.998. This fact indicates that the experimental log Kex± values clearly reflect the log Kex± S ones at Δφeq = 0. The result is the same as that [1] reported before for the AgPic extraction by B15C5 and B18C6 into DCE or DCM. On the other hand, in this study, we were not able to obtain the log Kex2± values which are comparable to the above log Kex± ones.
Accordance of Δφeq with the distribution of ML2+ into NB
The individual distribution constants (KD,ML) of ML2+ into the NB phase can be evaluated from the other thermodynamic cycle, Kex± = KMLKD,MLK1,org(KD,A)2/KD,L (Table 2). Here, KML and KD,L (Table 1) are defined as [ML2+]/[M2+][L] and [L]o/[L] [15], respectively, and these values at 298 K were available from references; log KM18C6 = 0.48 for M = Ca, 2.72 for Sr and 3.87 for Ba [4]; log KMB18C6 = 0.48 for M = Ca, 2.41 for Sr and 2.90 for Ba [21,22]; log KD,L = −1.00 [18] for L = 18C6 and 1.57 [20] for B18C6. Using the logarithmic form of the above equation, we obtained log KD,M18C6 = 0.88 for M = Ca, −0.17 for Sr and −0.99 for Ba and log KD,MB18C6 = 2.62 for M = Ca, 1.44 for Sr and 1.61 for Ba. There was a tendency that these values increase with an increase in the log KD,ML S ones: log KD,ML = (1.61 0.50)log KD,ML S + (3.67 ± 0.92) at R = 0.848. Here, the log KD,ML values [20] determined in terms of ion-transfer polarography were employed as log KD,ML S. Also, the Δφeq values can be easily evaluated from a modified form, log KD,ML = 2(Δφeq/0.05916) + log KD,ML S, of the relation in Table 1: Δφeq = 0.088 V for the CaPic2-18C6 system, 0.060 for SrPic2-18C6, 0.047 for BaPic2-18C6, 0.12 for CaPic2- B18C6, 0.081 for SrPic2-B18C6 and 0.071 for BaPic2-B18C6 at 298 K. These Δφeq values were in good agreement with those listed in Table 4. This fact indicates that the expression of Kex± and KD,Pic by Δφeq in the MPic2 extraction systems with L into NB does not conflict with the data [20] obtained from the electrochemical measurements. Additionally, the Δφex± 0′ values calculated from the relation in Table 1 were well reproduced by the Δφ-relation (b) in Table 2.
Expressions of the extraction constants by Δφeq were extended into Kex±, Kex2± and Kex of the MIIPic2 extraction systems with L, in addition to Kex± and Kex of the AgPic-L systems [1]. These expressions were summarized in Tables 1 and 2. However, the matters for precision of the values in the analyses have been present for the determination of Kex2± S. Also, there may be self-inconsistency for the estimation of the Kn,NB values. It was demonstrated that the log Kex± values well reflect the log Kex± S ones. So, one can see markedly the relation between Kex± obtained from an extraction experiment and Kex± S from an electrochemical one. This result fundamentally enables us to discuss the extraction-ability and -selectivity of L against M2+ from both the values. Moreover, it was shown that the expressions of Kex±, KD,ML and KD,Pic by Δφeq do not conflict with data obtained from the electrochemical measurements.
The authors thank Mr. Shinichi Nakajima for his experimental assistance in the KMPic determination.
In practice, we have calculated the values of
log Kex± − log Kex2± S = f(Δφeq − Δφex± 0 ′) − log Kex2± S (A1)
from Equation (6) and the relation in Table 1. Rearranging this equation, the following equation can be easily obtained
log Kex± − log Kex2± S = log Kex± S − log Kex2± S + fΔφeq. (A2)
Also, Equation (7) gave
log Kex − log Kex± = log Kex S − log Kex± = log Kex S − f(Δφeq − Δφex± 0′)
= log Kex S − log Kex± S − fΔφeq (A3)
Log K1,NB and log K2,NB in Table 3 are equal to Equations (A2) and (A3), respectively. As examples, the log K1,NB and log K2,NB values for the SrPic2-B18C6 system were calculated from these equations to be 4.73 and 5.07, respectively. These values were in good accord with those listed in Table 3.
Why do Equations (A2) and (A3), the functions expressing log K1,NB and log K2,NB, contain Δφeq? This question comes from the fact that log Kn,NB (n = 1, 2) in Table 1 were derived from the condition of Δφeq = 0 V. Also, the above results are self-consistent to the fact that all the log Kn,NB values in Table 3 are conditional equilibrium-constants, such as Kn,NB fixed in an INB value. Unfortunately, the authors cannot now explain these inconsistencies.