Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2014) Volume 3, Issue 4
The 2008 financial crisis proved the “Great Moderation” (a period when it was believed that policymakers had successfully smoothed macroeconomic fluctuations) to be transitory. Understanding a country’s degree of susceptibility to these fluctuations is crucial to investors but previous studies have shown that increasing trade and financial openness can have ambiguous effects. This paper examines a set of 11 countries individually, before the financial crisis, modeling variability in output, consumption, and investment as functions of both openness and external volatility. Financial openness tends to reduce investment volatility for the countries in this sample, while consumption is relatively unaffected overall. Output variability registers mixed results. The regression results are then examined to find relationships with various economic, development, and institutional-quality indicators. Trade openness is found to be correlated with a reduction in output volatility for less-developed countries and an increase for developed countries, while financial openness shows the opposite outcome.
<Much has been written about the “Great Moderation,” the precrisis period during which many countries’ output showed relatively little fluctuation. This low volatility was attributed to policymakers’ skill, before the 2008 global financial crisis proved these events to be temporary. Yet even during relatively stable times, many countries have experienced substantial variation in real macroeconomic activity. Such fluctuations in output, consumption, and investment can have tangible welfare effects, as people face increased risk and, per the socalled “compensation hypothesis,” turn to the government for transfers to alleviate it. While the idea of the Great Moderation is now relegated to memory, it is important to examine how transmission channels can differ from country to country, even during the most stable, bestmanaged times and outside of once-in-a-lifetime crisis periods. To this end, we examine macroeconomic volatility and its transmission channels for a set of 11 countries using the longest available datasets— but end our estimations at the end of 2007. We find that each country behaves differently, and that these idiosyncrasies might be explained by various measures of development. These findings provide specific, country-level results, that support a number of earlier, but broader, analyses.
Many important studies have focused on the growth-volatility relationship, finding that volatility itself is a cause, rather than an effect, of macroeconomic performance. Ramey and Ramey (1995), Edwards (2007), and Imbs (2007) generally find a positive relationship between the two, but this is by no means universal. Most recently, Miller and Fang [1] discuss the Great Moderation in the U.S., but find no relationship between output growth and volatility.
Other studies, both theoretical and empirical, have found that increasing economic openness can have an impact on macroeconomic volatility, but that its effects can be mixed. Openness can serve as a transmission mechanism whereby one country’s shocks can cause volatility in another, or as a means by which nations can pool risk and thus dampen shocks. Erturk [2], for example, shows theoretically that capital account liberalization might lead to increased macroeconomic volatility through financial flows. But not all macroeconomic indicators behave the same way: Evans and Hnatkovska [3] find that financial integration leads to an increase in output volatility, but that consumption volatility follows a “inverted U” pattern, with small welfare benefits as a result.
In their review article, Kose et al. [4] show that the contribution of openness on macroeconomic volatility is ambiguous. Empirical studies that use large panels of countries include Razin and Rose [5], who find no significant correlation between trade and financial openness and the volatility of output, consumption, and investment for 138 countries. Karras [6] examines two samples, which include as many as 105 countries up to 1998. Controlling for economic size, he finds that both size and trade openness have a negative effect on output, consumption, investment, and exchange-rate volatility. Hegerty [7,8] finds that “hot” non-FDI flows contribute to macroeconomic volatility in a set of emerging markets and transition economies, respectively.
In another seminal paper, Kose et al. [9] arrive at mixed results with a group of industrial countries and Less-Developed Countries (LDCs) up to 1999, finding that financial integration has led to a relative increase in consumption volatility compared to output volatility. They investigate the role of openness in these trends, proxying trade and financial openness with both de jure (measures of restrictions) and de facto (ratios of actual flows to GDP) measures. The authors include a large number of additional explanatory variables in their model, including per capita income and the standard deviation of countries’ terms of trade. Using instrumental variable and panel methods, they find that trade openness has led to an increase in output, consumption, and income volatility, and financial openness causes an increase in consumption volatility. The authors surmise that there is a threshold after which financial integration begins to cause a decrease in this variability. The volatility of the terms of trade, which represents external volatility, is shown to have a significantly positive impact on all volatility variables using both estimation techniques.
External volatility is potentially a bigger contributor to macroeconomic openness than economic openness. Hirata et al. [10] find that terms of trade shocks explain a large share of macroeconomic volatility in the Middle Eastern and North African countries of Egypt, Morocco, Tunisia, and Turkey. Kim [11] includes as many as 175 countries in a panel in an effort to separate openness from external risk over a period from 1950 to 2002. The volatilities of income, private consumption, and investment are modeled as functions of trade openness (exports, imports, or the sum of both, as a share of GDP) and financial openness (the share of gross private capital flows), as well as a number of measures of external risk. These include terms of trade and exchange-rate volatility and various political factors. The author then uses cross-section and panel methods to show that external risk has more of an effect on volatility than does economic openness.
While a large panel, applied to a specification that includes both openness and external volatility measures, is able to separate between the two, only a set of individual estimations will be able to fully isolate the mixed results that are prevalent in the literature. This study does so, estimating such a function for 11 individual countries using quarterly time-series data that end before the 2008 crisis. The resulting estimates are then evaluated further to address their underlying causes. This paper proceeds as follows: Section II provides a description of the data and econometric methodology, while Section III presents the empirical results. Section IV concludes.
This study uses time-series modeling to capture the individual experiences of a wide range of countries. Thus, it is able to expand on the general results that previous panel studies have found, by allowing for idiosyncracies among the countries while still looking for common patterns. To do this, quarterly data are taken from the International Financial Statistics of the International Monetary Fund for 11 countries. The start dates for each sample period (which ends in late 2007 in all cases) is given in Table 2. These countries are chosen because of the availability of data: Only they have the statistics required to create a key financial openness indicator.
IMF data include nominal GDP, consumption, and investment; the GDP deflator, Consumer Price Index, and Producer Price Index, by which the nominal values are (respectively) deflated; nominal dollar exchange rates; export and import price indices; exports and imports (c.i.f); and financial flow data. The availability of financial data is the main limiting factor of the sample used here, although for Portugal and Kazakhstan, quarterly financial flow data was available from the websites of their central banks.
The 11 countries include a large proportion of transition economies (Romania, Hungary, Belarus, and Kazakhstan). Within this set, however there is a rather wide disparity between the command economy of Belarus, and Hungary, which has been a European Union member for more than a decade. Likewise, there are two Scandinavian countries (Finland and Iceland), three advanced industrial countries (Australia, Portugal, and the United Kingdom), one South American nation (Peru), and one Middle Eastern country (Israel). While this sample is clearly not representative of the world—there are no African or Asian countries—it provides enough diversity to be able to arrive at some interesting results.
Table 1 outlines important macroeconomic characteristics for these countries. We see that Belarus and Hungary are very open to trade in goods and services, with Hungary’s level of openness increasing during this period; Iceland and Finland are much more financially open. Iceland’s figure portends the crisis that would follow soon after the estimation period ends. Australia, on the other hand, has a larger internal market, so its degree of openness is much smaller. These regional differences might help explain our results below.
| Country | Level of Trade Openness (% of GDP, 2004) | % Change (over sample) | Level of Financial Openness (% of GDP, 2004) | % Change (over sample) |
|---|---|---|---|---|
| Australia | 7.66 | 20 | 178.6 | 209.54 |
| Belarus | 130.96 | 5.61 | 137.4 | 26.91 |
| Finland | 58.8 | 27.95 | 1280.9 | 699.28 |
| Hungary | 111.99 | 48.3 | 535.61 | 122.05 |
| Iceland | 51.19 | -4.42 | 2965.62 | 818.02 |
| Israel | 57.17 | 30.26 | 547.94 | 135.79 |
| Kazakhstan | 59.52 | 95.67 | 218.71 | 519.86 |
| Peru | 33.54 | 127.93 | 299.03 | -4.54 |
| Portugal | 46.17 | 11.21 | 239.66 | 424.52 |
| Romania | 51.53 | 51.16 | 256.17 | 22.61 |
| United Kingdom | 44.69 | -12.29 | 1619.91 | 161.24 |
Calculated from the International Financial Statistics of the IMF.
Table 1: Levels and Growth Rates of Openness Variables.
These data are first used to construct the volatility terms. A number of different proxies for volatility have been used in the literature. While time-varying GARCH methods are popular, they require higherfrequency data than are available here. Thus, a commonly-used method is chosen for this study: volatility in a given variable Z is thus calculated as the moving average of the standard deviation of its log changes, as in Fang and Miller [1]:
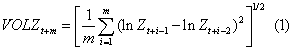
Because the data used here are quarterly, m is chosen to equal 4. Possible correlation among the observations, created through this volatility measure, is controlled for in the estimation procedure. The volatilities of output, consumption, and investment, as well as terms of trade and the exchange rate, are created for each country.
The Economic Model
Econometrically, the volatilities of real income, consumption, and investment are each modeled individually as functions of trade openness, financial openness, external volatility, and exchange-rate volatility:
VOL=f (OPEN,FINOPEN,VOLE,VOLX) (2)
The model structure and the explanatory variables are based on Kose [9] and Kim [11]. Following Kose et al. [9], trade openness (OPEN) is defined as each country’s exports plus imports as a share of GDP. Financial openness (FINOPEN) is defined as the sum of foreign direct investment, portfolio investment, and other investment, both as a donor and as a recipient, as a share of GDP. VOLE is the volatility of a country’s terms of trade (export prices divided by import prices), weighted by each country’s ratio of exports to imports. In cases where an export price or import price index is not available, a substitute measure from the IFS is applied. Finally, VOLX is the volatility of each country’s nominal U.S. dollar exchange rate.
Using these variables, the models are estimated with the Dynamic Ordinary Least Squares (DOLS) technique of Stock and Watson [12]. The model is as follows:
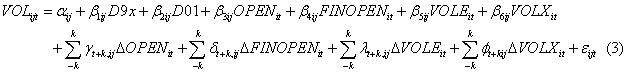
Dummy variables are included for either the Asian Crisis of 1997q3 or (for the four transition economies) the Russian Crisis of 1998q3, as well as for the global macroeconomic shock of 2001q4. These variables equal one during the relevant quarter and zero otherwise. A total of 33 equations are estimated separately.
Unit-root testing is first conducted via the Augmented Dickey- Fuller test (with lags chosen by estimating first at four lags and then re-estimating at the maximum significant lag), the Phillips-Perron [13] test (which controls for autocorrelation by using Newey-West standard errors), and the Zivot-Andrews [14] test (which allows for an endogenous structural break). The results of these tests show that while some of these variables are clearly nonstationary, others may or may not be stationary (particularly at different significance levels). The DOLS procedure controls for this by incorporating the leads and lags of the differences of the explanatory variables into a standard OLS regression. This procedure has been shown by Montalvo [15] to work well in small samples, which is beneficial for those countries where the length of the sample is around 10 years. It also uses Newey-West autocorrelation-robust standard errors, which will control for possible autocorrelation in the volatility measures.
This equation is used to estimate j=3 types of macroeconomic volatility for each of i=11 countries. Estimation begins with k=0. The model is estimated, and the residuals are tested for stationarity. If the ADF test indicates nonstationarity (at a lag length chosen through the truncation method mentioned above), k is increased by one. If the residuals are stationary, the cointegrating regression is reported. If, at k=3, the residuals are still nonstationary, it is deemed that there is no cointegrating vector. The short-run (difference) variables in the regression are present only to control for nonstationarity, and are thus not reported.
Since these time-series results are shown to vary widely among the countries, the next step is to try to discern whether any country characteristics are correlated with these results. This is done with a Spearman correlation coefficient:
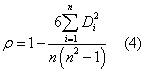
This simple nonparametric test looks for a relationship between two variables of interest. Here, n=11, and Di is the difference in rank between ordered lists of two characteristics. If the list contains exactly matching ranks for two characteristics (perfect correlation), then Di would be zero, and ρ would equal one. The more the rankings fail to match, the lower ρ will be. Whereas a certain amount of random mismatching would indicate an absence of any relationship at all, at some point the columns will differ to a degree that cannot be attributed to chance. At this point, the statistic becomes significantly negative.
This study attempts to find a correlation between the time-series (regression) results and country characteristics. The regression results for OPEN and FINOPEN (for each of the 11 countries) are ranked, and compared to ranked lists of six different country characteristics. These characteristics represent characteristics of the variables themselves, as well as indicators of institutional quality and economic well-being. They are: The level of the pertinent openness measure (2004, period average); the growth rate of this openness measure (from q3 in the first year in the sample to q3 in the final year); a measure of institutional quality (LAW, the World Bank World Governance Law and Order indicator, 2007); the UN Human Development Index, (2004), HDI; GDP (in dollars, 2004, period average); and GDP per capita (2004, period average), GDPC. In all cases, 1=the wealthiest, fastest-growing, or most developed country in the list, and 11=poorest or least developed in the category.
The ranking of the regression results for OPEN and FINOPEN is designed to capture whether the fact that a developed country responds positively to openness while a less-developed country responds negatively, or vice versa, is related to a certain country characteristic. Thus, the results must be ranked with “most positive” at one end, and “most negative” at the other. This is done here by ranking the p-values from the DOLS regression. A ranking of 1 is given to a positive coefficient with the lowest p-value, and a ranking of 11 is given to the negative coefficient with the lowest p-value. In the middle are the p-values for the positive yet insignificant coefficients, ranked before (lower than) the p-values for the negative yet insignificant coefficients. If a specification is shown not to be cointegrated, it is treated as if it had p=1.000. Figure 1 shows this relationship. Once these paired lists are created, they are used to create correlation coefficients. If the coefficient for ρ exceeds its critical value, then it can be said that there is a significant correlation (significantly positive or negative) between the results and the specific country characteristic. This correlation is explained below.
First, the ADF, Phillips-Perron, and Zivot-Andrews stationarity tests are conducted. As Table 2 shows, the three tests often do not agree with one another. Some variables are clearly nonstationary (such as trade openness for Belarus and consumption volatility for Finland, Israel, and Peru). Other variables vary by test. It is possible that certain variables that are found to be stationary by the Zivot-Andrews test (such as Hungarian financial openness) contain a structural break that is overlooked by the other tests. In other cases (marked with a single asterisk), a variable is stationary at 5 percent, but not 1 percent. Still others might be significant at 10 percent. This “borderline” stationarity makes the application of traditional cointegration tests, such as the Johansen and Juselius [16] method, problematic. The DOLS method, on the other hand, is able to incorporate I(0) variables. The estimation results are presented in Table 3.
| Country (start date) | Variable | ADF | # lags | P-P | 1% | 5% | Z-A | Break |
|---|---|---|---|---|---|---|---|---|
| Australia | VOL(Y) | -2.128 | 4 | -3.888* | -3.53 | -2.901 | -4.925* | 1993q1 |
| (1986q2) | VOL(C) | -2.807 | 4 | -3.685* | -3.53 | -2.901 | -5.199* | 1997q3 |
| VOL(I) | -2.84 | 4 | -4.236* | -3.53 | -2.901 | -6.035** | 2000q4 | |
| OPEN | -1.907 | 4 | -2.176 | -3.53 | -2.901 | -3.649 | 2003q1 | |
| FINOPEN | 1.681 | 3 | 0.769 | -3.531 | -2.902 | -1.923 | 1994q1 | |
| VOL(E) | -3.301* | 4 | -3.817** | -3.53 | -2.901 | -6.187** | 2004q2 | |
| VOL(X) | -3.45* | 4 | -3.730** | -3.53 | -2.901 | -5.583** | 1997q4 | |
| Belarus | VOL(Y) | -0.757 | 1 | -0.83 | -3.634 | -2.952 | -4.486* | 2001q2 |
| (1996q4) | VOL(C) | -3.299* | 3 | -1.7 | -3.634 | -2.952 | -3.14 | 2001q4 |
| VOL(I) | -1.361 | 1 | -1.059 | -3.634 | -2.952 | -2.731 | 2005q3 | |
| OPEN | -3.954** | 1 | -4.222** | -3.628 | -2.95 | -6.748** | 2000q2 | |
| FINOPEN | -2.043 | 4 | -3.288* | -3.634 | -2.952 | -3.837 | 1999q2 | |
| VOL(E) | -2.077 | 4 | -2.504 | -3.621 | -2.947 | -3.907 | 2005q1 | |
| VOL(X) | -1.742 | 1 | -1.481 | -3.614 | -2.944 | -4.27 | 2001q2 | |
| Finland | VOL(Y) | -2.036 | 1 | -2.063 | -3.508 | -2.89 | -3.618 | 1996q2 |
| (1981q2) | VOL(C) | -3.959** | 3 | -3.439* | -3.508 | -2.89 | -5.049* | 2004q1 |
| VOL(I) | -0.705 | 4 | -1.108 | -3.508 | -2.89 | -4.555 | 2004q1 | |
| OPEN | -2.239 | 4 | -1.361 | -3.508 | -2.89 | -3.295 | 1987q2 | |
| FINOPEN | -2.556 | 4 | 0.22 | -3.508 | -2.89 | -4.893* | 1999q2 | |
| VOL(E) | -0.61 | 4 | -3.050* | -3.508 | -2.89 | -5.527* | 1990q4 | |
| VOL(X) | 0.29 | 1 | -3.997** | -3.508 | -2.89 | -6.613** | 1993q1 | |
| Hungary | VOL(Y) | -2.516 | 4 | -2.314 | -3.621 | -2.947 | -3.335 | 2006q1 |
| (1997q1) | VOL(C) | -2.524 | 1 | -2.649 | -3.621 | -2.947 | -3.511 | 2002q4 |
| VOL(I) | 0.466 | 4 | -0.178 | -3.621 | -2.947 | -2.876 | 2006q1 | |
| OPEN | -1.792 | 4 | -2.37 | -3.628 | -2.95 | -4.235 | 2001q3 | |
| FINOPEN | 1.043 | 4 | 1.617 | -3.634 | -2.952 | -6.537** | 2005q4 | |
| VOL(E) | -1.093 | 4 | -2.573 | -3.621 | -2.947 | -3.362 | 2002q4 | |
| VOL(X) | -5.343** | 3 | -3.099* | -3.621 | -2.947 | -4.464 | 2004q1 | |
| Iceland | VOL(Y) | -1.857 | 4 | -2.343 | -3.668 | -2.966 | -3.909 | 2003q2 |
| (1998q2) | VOL(C) | -2.376 | 4 | -2.691 | -3.668 | -2.966 | -5.408* | 2005q3 |
| VOL(I) | -2.866 | 1 | -1.731 | -3.668 | -2.966 | -4.222 | 2000q2 | |
| OPEN | -2.434 | 4 | -4.591** | -3.675 | -2.969 | -6.166** | 2002q3 | |
| FINOPEN | -1.103 | 4 | 4.835** | -3.675 | -2.969 | -2.554 | 2005q4 | |
| VOL(E) | -1.576 | 4 | -2.732 | -3.662 | -2.964 | -3.323 | 2003q3 | |
| VOL(X) | -2.181 | 4 | -2.137 | -3.655 | -2.961 | -4.049 | 2000q4 | |
| Israel | VOL(Y) | -2.559 | 4 | -3.859** | -3.545 | -2.91 | -4.743 | 1996q2 |
| (1989q2) | VOL(C) | -3.026* | 4 | -3.594** | -3.545 | -2.91 | -5.431** | 1995q1 |
| VOL(I) | -2.114 | 4 | -2.581 | -3.545 | -2.91 | -4.432 | 2004q4 | |
| OPEN | -0.746 | 2 | -1.618 | -3.546 | -2.911 | -3.706 | 1994q4 | |
| FINOPEN | 1.241 | 4 | 1.94 | -3.546 | -2.911 | -2.568 | 1994q3 | |
| VOL(E) | -2.814 | 4 | -2.946* | -3.545 | -2.91 | -3.999 | 2002q3 | |
| VOL(X) | -3.013* | 4 | -3.885** | -3.545 | -2.91 | -5.571** | 1999q1 | |
| Kazakhstan | VOL(Y) | -1.084 | 4 | -2.603 | -3.668 | -2.966 | -4.156 | 2002Q2 |
| (1998q2) | VOL(C) | -1.164 | 4 | -2.241 | -3.668 | -2.966 | -3.233 | 2002Q4 |
| VOL(I) | -2.154 | 4 | -1.961 | -3.668 | -2.966 | -2.853 | 2006Q1 | |
| OPEN | -3.757** | 4 | -2.275 | -3.675 | -2.969 | -4.372 | 1999Q4 | |
| FINOPEN | -1.356 | 2 | -1.307 | -3.675 | -2.969 | -5.406* | 2000Q4 | |
| VOL(E) | -2.362 | 1 | -2.419 | -3.668 | -2.966 | -4.472 | 2005Q2 | |
| VOL(X) | -1.943 | 4 | -2.398 | -3.668 | -2.966 | -5.370* | 2000Q3 | |
| Peru | VOL(Y) | -1.892 | 4 | -3.262* | -3.559 | -2.918 | -7.275** | 2001q3 |
| (1991q1) | VOL(C) | -9.423** | 4 | -10.657** | -3.559 | -2.918 | -9.974** | 1993q4 |
| VOL(I) | -3.31 | 3 | -4.710** | -3.559 | -2.918 | -4.674 | 2004q3 | |
| OPEN | 1.258 | 4 | 0.36 | -3.56 | -2.919 | -3.177 | 2004q2 | |
| FINOPEN | -2.959* | 4 | -4.064** | -3.56 | -2.919 | -4.418 | 1998q4 | |
| VOL(E) | -3.616** | 1 | -3.129* | -3.559 | -2.918 | -4.617 | 2002q4 | |
| VOL(X) | -4.351** | 4 | -7.571** | -3.555 | -2.916 | -82.21** | 1994q1 | |
| Portugal | VOL(Y) | -1.225 | 4 | -2.175 | -3.6 | -2.938 | -4.481 | 2000Q2 |
| (1996q1) | VOL(C) | -2.416 | 1 | -2.555 | -3.6 | -2.938 | -3.28 | 2000Q2 |
| VOL(I) | -1.786 | 4 | -2.708 | -3.6 | -2.938 | -4.392 | 2001Q1 | |
| OPEN | -1.587 | 1 | -2.986* | -3.6 | -2.938 | -3.542 | 2005Q4 | |
| FINOPEN | -0.737 | 4 | 0.132 | -3.6 | -2.938 | -2.968 | 2003Q2 | |
| VOL(E) | -1.581 | 4 | -2.548 | -3.6 | -2.938 | -4.538 | 2004Q1 | |
| VOL(X) | -2.223 | 4 | -2.431 | -3.6 | -2.938 | -3.073 | 2006Q1 | |
| Romania | VOL(Y) | -0.472 | 4 | -0.57 | -3.662 | -2.964 | -4.653 | 2004Q1 |
| (1998q2) | VOL(C) | -2.297 | 4 | -2.763 | -3.662 | -2.964 | -6.249** | 2000Q2 |
| VOL(I) | -0.889 | 4 | -1.453 | -3.662 | -2.964 | -2.213 | 2003Q2 | |
| OPEN | -2.79 | 4 | -4.229** | -3.668 | -2.966 | -5.376* | 2000Q3 | |
| FINOPEN | -5.449** | 4 | -11.013** | -3.689 | -2.975 | -3.129 | 2001Q2 | |
| VOL(E) | -1.016 | 4 | -2.261 | -3.662 | -2.964 | -6.340** | 2003Q1 | |
| VOL(X) | -1.892 | 4 | -1.75 | -3.662 | -2.964 | -5.580** | 2005Q1 | |
| United Kingdom | VOL(Y) | -2.41 | 4 | -3.056* | -3.517 | -2.894 | -6.119** | 1989q2 |
| (1984q1) | VOL(C) | -1.801 | 4 | -2.919* | -3.517 | -2.894 | -5.510** | 1988q4 |
| VOL(I) | -1.888 | 4 | -3.143* | -3.517 | -2.894 | -5.358* | 1990q1 | |
| OPEN | -4.283** | 4 | -3.673** | -3.517 | -2.894 | -3.715 | 1993q2 | |
| FINOPEN | 2.068 | 1 | 2.208 | -3.52 | -2.896 | -1.919 | 1989q4 | |
| VOL(E) | -2.226 | 4 | -3.951** | -3.517 | -2.894 | -5.535* | 2004q4 | |
| VOL(X) | -1.764 | 4 | -3.193* | -3.517 | -2.894 | -8.241** | 1994q3 |
Critical Values for ADF test: 1%:-3.54, 5%: -2.95; for Zivot-Andrews (Z-A) test: 1%:-5.33, 5% -4.80.
P-P=Phillips-Perron test. Break=point with minimum t-value in the A-Z test.
**and *: significant at 1 and 5 percent, respectively.
Table 2: Stationarity Test Results.
| VOL(Y) | D9x | D01 | OPEN | FINOPEN | VOLE | VOLX | ADF | Order | k |
|---|---|---|---|---|---|---|---|---|---|
| Australia | 0.005 (0.028) | -0.008 (0.013) | 0.675 (0.177) | -0.012 (0.004) | 0.031 (0.782) | 0.164 (0.154) | -4.239 | 1 | 4 |
| Belarus | -0.032 (0.000) | -0.008 (0.027) | -0.017 (0.468) | 0.020 (0.048) | 0.034 (0.514) | -0.131 (0.000) | -4.812 | 0 | 1 |
| Finland | 0.012 (0.003) | -0.012 (0.001) | 0.044 (0.177) | -0.001 (0.113) | 0.183 (0.001) | -0.131 (0.219) | -3.817 | 3 | 1 |
| Hungary | -0.023 (0.053) | 0.026 (0.071) | 0.011 (0.700) | 0.005 (0.007) | 1.441 (0.000) | -0.691 (0.101) | -3.996 | 0 | 1 |
| Iceland | 0.007 (0.632) | 0.432 (0.042) | -0.002 (0.001) | -0.021 (0.881) | 0.328 (0.322) | -3.716 | 0 | 1 | |
| Israel | -0.007 (0.149) | 0.008 (0.043) | 0.060 (0.244) | -0.002 (0.394) | -0.103 (0.158) | -0.023 (0.832) | -4.434 | 2 | 1 |
| Kazakhstan | 0.033 (0.417) | -0.075 (0.726) | -0.014 (0.469) | -0.027 (0.879) | -0.049 (0.903) | -4.152 | 0 | 1 | |
| Peru | -0.004 (0.832) | 0.051 (0.119) | 0.209 (0.363) | 0.045 (0.299) | 0.003 (0.958) | 0.598 (0.298) | -5.023 | 0 | 4 |
| Portugal | -0.005 (0.708) | -0.007 (0.528) | -0.019 (0.955) | -0.012 (0.664) | 0.005 (0.994) | -0.045 (0.981) | -4.871 | 0 | 3 |
| Romania | 0.018 (0.308) | 1.338 (0.105) | -4.152 (0.103) | -1.003 (0.268) | 4.768 0.070) | -7.156 | 1 | 2 | |
| United Kingdom | -0.001 (0.173) | -0.002 (0.027) | 0.032 (0.116) | -0.000 (0.729) | -0.017 (0.533) | 0.010 (0.669) | -3.822 | 3 | 1 |
| VOL(C) | D9x | D01 | OPEN | FINOPEN | VOLE | VOLX | ADF | Order | k |
| Australia | 0.002 (0.222) | 0.0003 (0.85) | -0.063 (0.671) | -0.002 (0.466) | -0.013 (0.680) | 0.075 (0.012) | -4.810 | 3 | 1 |
| Belarus | -0.230 (0.070) | -0.175 (0.048) | 0.029 (0.864) | -0.153 (0.127) | -1.237 (0.066) | -0.194 (0.196) | -4.182 | 0 | 3 |
| Finland | 0.005 (0.002) | -0.012 (0.000) | 0.005 (0.772) | 0.0003 (0.500) | -0.056 (0.075) | -0.040 (0.261) | -3.941 | 0 | 0 |
| Hungary | -0.0005 (0.94) | -0.003 (0.900) | -0.076 (0.096) | 0.002 (0.655) | 0.148 (0.837) | -1.490 (0.104) | -4.296 | 3 | 2 |
| Iceland | 0.009 (0.260) | 0.062 (0.203) | -0.0002 (0.370) | -0.032 (0.494) | -0.201 (0.082) | -4.131 | 2 | 0 | |
| Israel | 0.006 (0.063) | 0.004 (0.426) | 0.003 (0.965) | 0.002 (0.495) | -0.073 (0.323) | 0.186 (0.095) | -5.356 | 2 | 0 |
| Kazakhstan | 0.027 (0.347) | -0.183 (0.447) | -0.027 (0.318) | -0.101 (0.644) | -1.485 (0.110) | -6.375 | 0 | 2 | |
| Peru | 0.005 (0.135) | 0.0001 (0.81) | 0.089 (0.011) | 0.020 (0.096) | 0.001 (0.923) | 0.001(0.984) | -5.843 | 0 | 1 |
| Portugal | -0.008 (0.765) | -0.016 (0.450) | -0.031 (0.964) | -0.014 (0.808) | 0.058 (0.967) | 0.946 (0.809) | -4.625 | 0 | 3 |
| Romania | 0.007 (0.721) | 0.013 (0.801) | 0.337 (0.097) | 0.048 (0.799) | -0.406 (0.115) | -4.817 | 2 | 0 | |
| United Kingdom | No Cointegrating Vector. | ||||||||
| VOL(I) | D9x | D01 | OPEN | FINOPEN | VOLE | VOLX | ADF | Order | k |
| Australia | -0.004 (0.356) | 0.004 (0.627) | 0.705 (0.229) | -0.011 (0.280) | -0.077 (0.530) | 0.204 (0.171) | -5.285 | 0 | 1 |
| Belarus | -0.062 (0.731) | 0.205 (0.242) | 0.852 (0.010) | -0.106 (0.469) | 0.205 (0.658) | -0.734 (0.001) | -6.038 | 0 | 2 |
| Finland | -0.023 (0.041) | -0.026 (0.000) | 0.050 (0.472) | -0.007 (0.000) | 0.233 (0.014) | 0.103 (0.626) | -3.906 | 0 | 1 |
| Hungary | -0.010 (0.315) | 0.009 (0.178) | 0.036 (0.121) | -0.025 (0.000) | -1.001 (0.007) | 1.263 (0.011) | -3.744 | 0 | 0 |
| Iceland | 0.008 (0.760) | -0.186 (0.398) | 0.002 (0.022) | 0.376 (0.177) | -0.214 (0.667) | -3.905 | 0 | 0 | |
| Israel | -0.026 (0.035) | -0.019 (0.147) | 0.167 (0.308) | -0.012 (0.020) | 0.210 (0.380) | 0.279 (0.552) | -4.805 | 3 | 0 |
| Kazakhstan | 0.015 (0.698) | -0.673 (0.009) | -0.045 (0.041) | -0.032 (0.866) | -1.188 (0.009) | -4.299 | 0 | 1 | |
| Peru | -0.034 (0.000) | -0.023 (0.000) | 0.028 (0.555) | -0.041 (0.039) | -0.043 (0.172) | 0.076 (0.000) | -3.964 | 0 | 0 |
| Portugal | -0.016 (0.645) | -0.021 (0.414) | -0.080 (0.921) | -0.024 (0.717) | 0.388 (0.802) | 1.601 (0.726) | -4.706 | 0 | 3 |
| Romania | 0.017 (0.547) | -0.718 (0.063) | 0.847 (0.368) | 0.369 (0.291) | -1.047 (0.292) | -4.702 | 0 | 1 | |
| United Kingdom | -0.013 (0.002) | -0.006 (0.216) | -0.136 (0.069) | -0.001 (0.031) | 0.029 (0.818) | -0.017 (0.888) | -3.682 | 0 | 2 |
p-values, based on Newey-West autocorrelation-consistent standard errors, are given in parentheses. Bold=significant at 10 percent (non-dummies).
99 percent critical value for the ADF test is -3.67.
Table 3: DOLS Results (p-values in parentheses).
The results in Table 3 show some interesting patterns. The dummy variables tend to be significant (mostly negative), but not in all cases. The 2001 shock appears to have had an impact on the output volatility of more countries than consumption or investment volatility. The 1990s shock (Asian or Russian crisis) seems to have an effect on an equal number of countries (four) for all three types of macroeconomic variability. Finland seems to have significant dummies in all cases, indicating that perhaps the country was especially influenced by these shocks.
The effects of openness (both trade and financial) and external shocks (both in the terms of trade and in the exchange rate) are of more interest, however. Of particular importance are the differences in behavior of the three types of volatility, the different responses to trade and financial openness, and the varying relative impact of openness and external volatility.
From the results shown in Table 3, we see that output and investment volatility demonstrate more response to changes in financial openness than does consumption volatility. The effects are more for output variability, but more countries are affected (usually negatively) for investment volatility. The four countries in which financial openness has an insignificant coefficient in the investment specification (Australia, Belarus, Portugal, and Romania) are about as different as countries in this sample can be. As a result, our first conclusion is that financial openness tends to reduce investment volatility, regardless of the country characteristics that are analyzed in this study. The fairly prevalent, yet mixed, effects on output volatility might be driven more by country characteristics, while the overall effects of openness on consumption variability are limited, perhaps due to consumption-smoothing. Only Peruvian consumption seems to be driven by both financial and trade openness.
Trade openness affects fewer countries in this sample than does financial openness. A larger proportion of the 11 countries registers an effect on investment (four out of 11, compared to two), and the p-value is lower than in the output or consumption specifications. For three countries, the effect of trade openness is negative, while for Belarus— which has a tightly controlled economy—trade openness appears to allow the transmission of volatility. The trade openness coefficient is significant only for a pair of countries in the other two specifications, and this is often at the 10 percent (or slightly higher) significance level. A second conclusion from these results is thus that while trade openness has some impact on variability, especially in investment, this effect is relatively weak. The coefficients tend to be weakly positive for output volatility, more strongly negative for investment volatility, and in between for consumption.
Since economic openness does not appear to influence macroeconomic volatility in all cases, it is possible that these fluctuations are instead driven by external risk. These effects seem to be limited, however. Terms-of trade volatility only affects a pair of countries in each of the three specifications. Finland and Hungary seem to be affected in all three specifications, although the signs are mixed. Exchange-rate volatility also appears to have an impact on Hungarian macroeconomic volatility, although the sign again varies across specifications. While terms of trade variability has a positive effect on output volatility, exchange-rate risk has a (weakly) negative impact. These signs are exactly reversed for the investment specification.
Since we arrive at mixed results, we can make some inferences about the role of country characteristics. We find that output has the most “ambiguous” results, since it appears at first glance that the effects of economic openness are limited for consumption and that the effects of trade and financial openness on investment volatility are predominantly negative. Thus, the specification for output volatility provides the most room for country characteristics to be evaluated.
The output specifications for Australia and Iceland (which was hit hard by the 2008 crisis) have significantly negative coefficients for financial openness, while Belarus and Hungary have positive coefficients. Perhaps there is something about integration in transition economies that encourages volatility transmissions. To formally investigate whether wealthier countries do indeed behave differently than others, the Spearman correlation coefficients are calculated for the output, consumption, and investment volatility results for all six characteristics.
Before proceeding, it is important to discuss two key features of this analysis. First, as a nonparametric statistical technique, this approach makes few assumptions about sample size, distributions, or other characteristics that are common to standard (parametric) analyses. This is important in understanding the underlying setup of these estimates. Second, we must clarify exactly what a significantly positive or negative coefficient means. A ranking of 1 is assigned both to the country with the most significantly positive openness coefficient, as well as to the country with the fastest growth, highest income, or highest level of development. Likewise, a ranking of 11 is given to the country with the most significantly negative coefficient, as well as the lowest growth, income, or level of development. Thus, a positive ρ indicates that a country’s well-being is correlated with increases in volatility as a result of openness (volatility transmissions), while a negative ρ indicates that higher well-being is correlated with decreases in volatility (volatility smoothing). The coefficients and their critical values are given in Table 4.
| Output | Consumption | Investment | ||||
|---|---|---|---|---|---|---|
| Variable | OPEN | FINOPEN | OPEN | FINOPEN | OPEN | FINOPEN |
| GROWTH | -0.257 | -0.536 | -0.018 | -0.491 | -0.136 | 0.084 |
| LEVEL | -0.484 | -0.209 | -0.209 | 0.373 | 0.255 | -0.28 |
| LAW | 0.68 | -0.564 | 0.1 | 0.009 | -0.027 | -0.025 |
| HDI | 0.552 | -0.527 | -0.073 | -0.246 | 0.182 | 0.007 |
| GDP | 0.316 | -0.127 | -0.3 | 0.309 | 0.018 | -0.439 |
| GDPC | 0.721 | -0.589 | 0.084 | -0.007 | -0.134 | -0.071 |
Note: n=11. At the 10% significance level, the critical value for significance is 0.536.
Bold=significant at 10 percent.
This value is from Hollander and Wolfe [17], Table A.31, two-sided critical values with n=11.
Table 4: Spearman Correlation Coefficients.
As expected, the specifications for consumption and investment show little correlation with the selected country characteristics. Output volatility does demonstrate certain significant relationships, however. First, growth in FINOPEN has a strong negative correlation with output volatility. Thus, it appears that countries that are experiencing rapid financial integration tend to also see smoother fluctuations in output as a result of this increasing openness. The same cannot be said for trade openness, however.
Secondly, various measures of institutional quality and economic development have opposite correlations for trade and financial openness. Increasing trade openness has a positive correlation with law and order, so it appears to facilitate volatility transmissions for those countries with better institutional quality. Increasing financial openness seems to have the opposite effect, smoothing volatility for countries with better institutional quality and allowing transmissions for those that are worse off.
The same pattern holds for per-capita income, with a positive ρ for trade openness and a negative ρ for financial openness. It also holds for the level of economic development (proxied by HDI). As a result, one can conclude that trade and financial openness have different effects on output volatility for countries at different levels of well-being. Trade openness helps reduce volatility for less-developed countries, while financial openness helps increase it. For more developed countries, trade openness facilitates volatility transmissions, while financial integration facilitates smoothing. This hints at the results of Kose et al. [9], who find evidence of a threshold after which financial openness begins to result in reduced variability.
What might drive these results? One explanation might have to do with exposure to exchange-rate volatility. For three of the countries where financial openness has an impact on output volatility, VOLX has a significant coefficient of the opposite sign. Perhaps financial integration is able to counteract the effects of external risk. Since these three countries are in Eastern Europe, it is possible that transition economies are exposed to particular risk.
Because trade and financial openness work through different channels, they can have varying effects on such a range of countries. The impact of trade openness can be mitigated by a flexible exchange rate. If one country experiences an output increase, for example, imports should increase, thereby increasing exports (and output) for a trading partner. A flexible rate, however, might weaken this shock, as depreciation should take place in the first country. Thus, countries that face exchange-rate volatility might also face a different exposure to the trade channel relative to the financial channel.
There are other possible explanations besides differences and interactions in the variables themselves. Since trade facilitates technology transfer in LDCs, it is plausible that the trade channel does have a beneficial effect on these countries. The re-orientation of trade flows in transition economies is at least coincident with, if not partially a cause of, macroeconomic stabilization in these countries. Likewise, less-developed countries face the prospect of sudden capital outflows, which can wreak havoc. Increased financial openness can contribute to this risk. Thus these results—that trade openness might help reduce output volatility in less-developed countries, while financial openness might help reduce output volatility in more-developed countries— correspond with what can be expected theoretically.
Economic openness, particularly financial openness, has been growing rapidly worldwide since the 1970s. More recently, macroeconomic volatility has increased greatly, destabilizing a number of countries and leading to a global crisis. The effects that this type of interconnection can have on a domestic economy can be mixed, however. Various studies have found that openness can either help reduce macroeconomic volatility through risk-sharing, or facilitate volatility transmissions. Empirical analyses have found mixed results for large panels of countries, often finding that external risk has a bigger influence on fluctuations than openness itself.
This study uses Dynamic Ordinary Least Squares to analyze quarterly time-series data for 11 countries individually, with three types of volatility modeled as functions of trade openness, financial openness, terms of trade risk, and exchange-rate volatility. Trade openness appears to have less of an impact than financial openness, and both types of external risk have a limited effect on macroeconomic volatility. Of the three types of volatility, consumption is shown to be affected the least by economic openness, while investment variability tends to be reduced by increasing financial openness. The effects of openness on output volatility are mixed. While this study focus exclusively on the pre-2008 period, the potential for a global crisis is clear, particularly when global channels for transmission are considered.
The DOLS results are then compared to six economic and development characteristics for the 11 countries. A set of Spearman correlation coefficients is constructed for pairs of ranked lists of the trade and financial openness results, alongside these characteristics. The output results show clear correlations. Fast growth in financial openness is correlated with a reduction in output volatility. At the same time, institutional quality, GDP per capita, and the level of economic development have correlations of opposite signs for trade and financial openness. Trade openness appears to be correlated with a reduction in output volatility for LDCs, while financial openness is correlated with this smoothing for those nations with higher income, more rapid integration, or a higher level of development or institutional quality.
These results suggest that policymakers, particularly in developing countries, might wish to focus more on trade integration than on financial integration as a development strategy, at least at first. Until a country reaches the “high” level of development, financial integration offers a channel for destabilizing transmissions of shocks, while trade channels work in the opposite direction. Policies such as free trade combined with capital controls—which led to sustained growth in China and elsewhere—might lead to macroeconomic stability as well.