Drug Designing: Open Access
Open Access
ISSN: 2169-0138
ISSN: 2169-0138
Research - (2021)Volume 10, Issue 2
Investment cost; Genetic algorithm; Gaussian process modeling; Batch process; Optimal design
In chemical engineering, there has been an increased interest in the development of systematic method for the design of batch process in specialty chemicals, food products, and pharmaceutical industries [1]. Most processes in the modern biotechnology industry correspond to batch plants and with the rapid development of new products (i.e. both therapeutic and non-therapeutic proteins) [2].
The main host for recombinant proteins for many years has been Escherichia coli. However, the developments with yeast cells have grown at a very rapid pace, which has resulted in several important commercial products such as insulin, hepatitis B vaccine, and also more recently, chymosin and protease. The fact that many recombinant proteins made in yeast can be made to be secreted out of the cell and that yeast allows for at least partial glycosilation is an added bonus for this host [3], therefore, in the optimal design of a multiproduct batch chemical process, the production requirement of each product and the total production time available for all products are specified. The number and size of parallel equipment units in each stage as well as the location and size of intermediate storage are to be determined in order to minimize the investment cost.
The common approach used by previous research in solving the design problem of batch plant has been to formulate it as a Mixed Integer Nonlinear Programming (MINLP) problem and then employ optimization techniques to solve it. Robinson and Loonkar studied the problem of designing multiproduct plants operating in single product campaign mode and with a single unit in each processing stage and they extended the nonlinear programming model to include both the design of discrete equipment size and the selection of the parallel units number, by solving it through the use of heuristics and branch and bound [4]. The same problem was further formulated by Grossmann and Sargent as a (MINLP) model [5]. Knopf et al. and Yeh et al. accounted for the presence of semicontinuous units [6,7]. Voudouris and Grossmann proposed reformulations of the previous design models where discrete sizes are explicitly accounted for [8].
Many works in the literature on batch process design are based on expressions that relate the batch sizes linearly with the equipment sizes. Also, the processing times are usually expressed as nonlinear functions of the batch size. Given certain restrictions on these mathematical expressions, the models can be referred to as posynomials, which possess a unique optimum [5]. Salomone and Iribarren proposed posynomial models in which the constants are obtained as a result of the optimization of the process decision variables with simplified models [9]. Salomone et al. generalized the approach by allowing the process parameters to be generated from either experimental data and/or dynamic simulation [10]. Because of the NP-hard nature of the design problem of batch plant, unbearable long computational time will be induced by the use of Mathematical Programming (MP) when the design problem is somewhat complicated. Severe initial values for the optimization variables are also necessary. Moreover, with the increasing size of the design problem, MP will be futile. Heuristics needs less computational time, and severe initial values for optimization variables are not necessary, but it may end up with a local optimum due to its greedy nature. Also, it is not a general method with respect to the fact that special heuristic rules will be needed for a special problem.
In economics, demand is the desire to own something and the ability to pay for it [11]. The term demand is also defined elsewhere as a measure of preferences that is weighted by income, but the market demand for such products is usually changeable, and at the stage of design of a batch plant, it is almost impossible to get the precise information on the future product demand over the lifetime of the plant. However, decisions must be made about the plant capacity. This capacity should be able to balance the product demand satisfaction. In the conventional optimal design of a multiproduct batch chemical plant [12], a designer specifies the production requirements for each product and total production time for all products [13]. The number required of volume and size of parallel equipment units in each stage is to be determined in order to minimize the investment cost.
Basically, batch plants are composed of items operating in a discontinuous way. Each batch then visits a fixed number of equipment items, as required by a given synthesis sequence (socalled production recipe) [14].
For instance, the design of a multiproduct batch chemical plant is not only to minimize the investment cost, but also to minimize: the operation cost, total production time, and to maximize: the revenue, flexibility index, simultaneously [15].
On the other hand, the key point in the Design of Multiproduct Batch Plants (DMBP) under uncertain demand. The market demand for products resulting from the batch industry is usually changeable, and at the stage of conceptual design of a batch plant, it is almost impossible to obtain the precise information on the future product demand over the plant lifetime. Nevertheless, decisions must be made about the plant capacity. This capacity should be able to balance the product demand satisfaction and extra-capacity in order to reduce the loss on the excessive investment cost or than on market share due to the varying product demands.
The most recent common approaches treated in the dedicated literature represent the demand uncertainty using fuzzy concepts with trapezoidal fuzzy number which can be represented by a membership function [16]. Yet, this assumption does not seem to be always a reliable representation of reality, because in practice we can’t get whole linguistics parameters about the uncertainty demand, such as perceptions, seasons and offers. For this reason an alternative treatment of the imprecision is constituted by using Gaussian Process Modeling that represents the “more or less possible values”.
In this work, we will only consider multiproduct batch plants, which means that all the products follow the same operating steps [17], the structure of the variables are the equipment sizes and number of each unit operation that generally take discrete values. The aim of this work is to solve the DMBP under uncertain demand using (GAs) with an effective mixed continuous discrete coding method with a four-point crossover operator. The model presented is general, it takes into account all the available options to increase the efficiency of the batch plant design: unit duplication in-phase and out-phase and intermediate storage tanks.
We proposed to apply GAs, an intelligent problem-solving method that has demonstrated its effectiveness in solving combinatorial optimization problem. Some modifications to traditional GAs, mainly an effective mixed continues discrete coding method with a four-point crossover operator is developed, and satisfactory results are obtained.
The paper is organized as follows; section 2 is devoted to the methodology. In section 3 we formulate the problem formulation, including process description. Then in section 4 we report results and discussion with comparative results. Finally the conclusions on this work are drawn.
In the 1960s and 1970s witnessed a tremendous development in the size and complexity of industrial organizations. The administrative decision-making has become very complex and involves large numbers of workers, materials and equipment. A decision is a recommendation for the best design or operation in a given system or process engineering, so as to minimize the costs or maximize the gains [18]. Using the term "best" implies that there is a choice or set of alternative strategies of action to make decisions. The term optimal is usually used to denote the maximum or minimum of the objective function and the overall process of maximizing or minimizing is called optimization. The optimization problems are not only in the design of industrial systems and services, but also apply in the manufacturing and operation of these systems once they are designed. Including various methods of optimization, we can mention: MINLP, Monte Carlo Method and Genetics Algorithms.
Genetic algorithms
The term genetic algorithms, almost universally abbreviated now a day to GAs, was first used by John Holland [19]. A genetic algorithms is a search technique used in computing to find exact or approximate solutions to optimization and search problems, however the canonical steps of the GAs can be described as follows:
The problem to be addressed is defined and captured in an objective function that indicated the fitness of any potential solution.
A population of candidate solutions is initialized subject to certain constraints. Typically, each trial solution is coded as a vector X, termed a chromosome, with elements being described as solutions represented by binary strings. The desired degree of precision would indicate the appropriate length of the binary coding.
Each chromosome, Xi, i=1,..., P, in the population is decoded into a form appropriate for evaluation and is then assigned a fitness score, μ(Xi) according to the objective.
Selection in genetics algorithms is often accomplished via differential reproduction according to fitness. In a typical approach, each chromosome is assigned a probability of reproduction, Pi, i=1,..., P, so that its likelihood of being selected is proportional to its fitness relative to the other chromosomes in the population. If the fitness of each chromosome is a strictly positive number to be maximized, this is often accomplished using roulette wheel selection [20]. Successive trials are conducted in which a chromosome is selected, until all available positions are filled. Those chromosomes with above-average fitness will tend to generate more copies than those with below-average fitness.
According to the assigned probabilities of reproduction, Pi, i=1,..., P, a new population of chromosomes is generated by probabilistically selecting strings from the current population. The selected chromosomes generate “offspring” via the use of specific genetic operators, such as crossover and bit mutation. Crossover is applied to two chromosomes (parents) and creates two new chromosomes (offspring) by selecting a random position along the coding and splicing the section that appears before the selected position in the first string with the section that appears after the selected position in the second string and vice versa (Figure 1). Bit mutation simply offers the chance to flip each bit in the coding of a new solution.
Figure 1: Four-points crossover operators.
The process is halted if a suitable solution has been found or if the available computing time has expired, otherwise, the process proceeds to step 3 where the new chromosomes are scored, and the cycle is repeated.
Implementation and empirical tuning methods:
Mapping objective functions to fitness form: In many problems, the objective is more naturally stated as the minimization of some cost function g(x) rather than the maximization of some utility or profit function u(x). Even if the problem is naturally stated in maximization form, this alone does not guarantee that the utility function will be non-negative for all (x) as we require in fitness function (a fitness function must be a non-negative figure of merit [20]. The duality of cost minimization and profit maximization is well known. In normal operations research work, to transform a minimization problem to a maximization problem we simply multiply the cost function by a minus one.
In genetic algorithm work, this operation alone is insufficient because the measure thus obtained is not guaranteed to be nonnegative in all instances. With GAs, the following cost-to-fitness transformation is commonly used:
f (x) = Cmax − g(x)
f (x) = 0
Where g(x)<Cmax
Otherwise, Cmax may be taken as the largest g value observed thus far. For the problem of DMBP in this paper, we take this transformation form.
Fitness scaling: In order to achieve the best results of GAs, it is
necessary to regulate the level of competition among members
of the population. This is precisely what we do when we perform
fitness scaling. Regulation of the number of copies is especially
important in small population genetic algorithms. At the start of
GAs runs, it is common to have a few extraordinary individuals in
a population of mediocre colleagues. If left to the normal selection rule 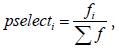 the extraordinary individuals would take
over a significant proportion of the finite population in a single generation, and this is undesirable, a leading cause of premature
convergence. Later on during a run, we have a very different
problem. Late in a run, there may still be significant diversity
within the population; however, the population average fitness
may be close to the population best fitness. If this situation is left
alone, average members and best members get nearly the same
number of copies in future generations, and the survival of the
fittest necessary for improvement becomes a random walk among
the mediocre. In both cases, at the beginning of the run and as the
run matures, fitness scaling can help.
the extraordinary individuals would take
over a significant proportion of the finite population in a single generation, and this is undesirable, a leading cause of premature
convergence. Later on during a run, we have a very different
problem. Late in a run, there may still be significant diversity
within the population; however, the population average fitness
may be close to the population best fitness. If this situation is left
alone, average members and best members get nearly the same
number of copies in future generations, and the survival of the
fittest necessary for improvement becomes a random walk among
the mediocre. In both cases, at the beginning of the run and as the
run matures, fitness scaling can help.
Constraints: We deal with the dimension constraints by coding equations and deal with time constraints this way: a genetic algorithm generates a sequence of parameters to be tested using the system model, objective function, and the constraints. We simply run the model, evaluate the objective function, and check to see if any constraints are violated. If not, the parameter set is assigned the fitness value corresponding to the objective function evaluation. If constraints are violated, the solution is infeasible and thus has no fitness.
Codings: When GAs manages a practical problem, the parameters of the problem are always coded into bit strings. In fact, coding designs for a special problem is the key to using GAs effectively. There are two basic principles for designing a GAs coding [20]:
1. The user should select a coding so that short, low order schemata are relevant to the underlying problem and relatively unrelated to schemata over other fixed positions.
2. The user should select the smallest alphabet that permits a natural expression of the problem.
Based on the characteristic and structure of DMBP, instead of choosing the concatenated, multiparamerted, mapped, fixed-point coding. A mixed continues discrete coding method with a fourpoint crossover operator is designed according to the two principles above. The coding method of a DMBP is as follows: Following the order-the numbers of out-of-phase groups in each batch stages, inphase parallel units in each of the groups, semi-continuous parallel units in each semi-continuous stages, the size of batch stages, semicontinuous stages, each parameter of the item size variables is encoded independently in usual binary codings (local strings), as it simplify the genetic operations, crossover and mutation. Then we place the highest bit of reach local string at the site from 1st to nth in DMBP chromosome and place the second highest bit of each local string at the site from (n+1)th to 2nth, and so on. Then we can obtain a DMBP chromosome (Figure 2).
Figure 2: Illustration of the encoding method for a small size example.
The reason for using crossed coding, because this codification is suitable for the item size variables, and can be analyzed in theory as follows:
• Because of the strong relationship among the parameters, the highest bit in each local string in binary codings determines the basic structure among every parameter, and the second highest bit in each local string determines finer structure among every parameter, and so on for the third, the forth, etc.
• The schema defining length under crossed coding (n) is shorter than the length under concatenated, mapped, fixedpoint coding (nK-K+1).
According to the schema theorem, short schemata cannot be
disturbed with high frequency; the schema under crossed coding
has a greater chance to be reproduced in the next generation. Due
to its combining the characteristics of function optimization with
schema theorem and successful binary alphabet table, crossed
coding demonstrates greater effectiveness than the ordinary coding
method in our implementation. Local string formation is achieved
this way: for a parameter x∈[xmin , xmax ] that needs to be coded,
transform it to a binary coding X ∈[0, 2k ] first (appropriate length
K is determined by the desired degree of precision) and then map
it to the specified interval [xmin, xmax]. In this way, the precision of this mapped coding may be calculated 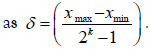 In fact,
this means that the interval from xminto xmax is divided into 2K-1
parts, because the biggest binary string that has a length of K equals
the decimal number 20 + 21 + 22 +...+ 2K−1 . Then, we can obtain x = xmin +δX, and a local string for parameter x with a length of K is obtained.
In fact,
this means that the interval from xminto xmax is divided into 2K-1
parts, because the biggest binary string that has a length of K equals
the decimal number 20 + 21 + 22 +...+ 2K−1 . Then, we can obtain x = xmin +δX, and a local string for parameter x with a length of K is obtained.
To illustrate the coding scheme to the size variables more clearly, we also want to give a simple example. For the minimization problem: min z = f (x, y) in which x∈[300,700] and y∈[700,1200] , if we adopt a string length of 5 for each local string and X:10110, Y: 01101 is an initial solution, we will get the chromosome 1001110001 (Figure 2) and obtain:
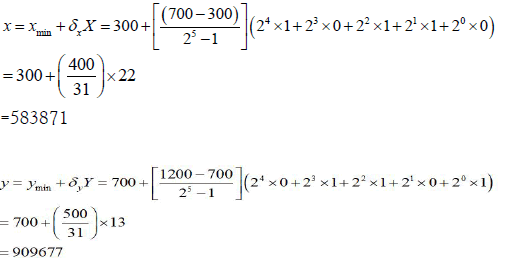
Although the item number per stage are copied just as they are worth in the chromosome (for instance, if nj=2, the corresponding locus will contain information “2”).The resulting configuration of a chromosome is shown in Figure 2. The final encoding procedure is adapted to the double nature of the variables: since continuous and integer variables have to coexist in the same chromosome, this latter is partitioned into two zones. As shown in Figure 2, the first zone encodes the continuous variables, i.e. the item sizes of each processing stage, as reduced variables, using crossed binary codings as explicated above. On the other hand, the integer variables, representing the item number for each stage, are copied directly in the chromosome without any change: for instance, the plant illustrated in Figure 2, has 2 items for stage 1, 1 item for stage 2, and 5 items for stage 3: This corresponds to the integer numbers encoded at the end of the chromosome: 2, 1, 5.
Reproduction: The reproduction operator may be implemented in algorithmic form in a number of ways. In this paper, we take the easiest methods Roulette wheel [20].
Crossover: Crossover operator can take various forms, i.e., onepoint crossover, multi-point crossover [21]. It is commonly believed that multi-point crossover has better performance. The number of crossover points in a multi-points crossover operator is determined by the string structure. In this paper, a four points crossover operator is adopted. The crossover rate plays a key role in GAs implementation. Different values for crossover rate ranging from 0.4 to 1.0 were tried, and the results demonstrate that the values ranging from 0.6 to 0.95. In this paper, we take 0.6 as a crossover rate.
Mutation operation: After selection and crossover, mutation is then applied on the resulting population, with a fixed mutation rate. The number of individuals on which the mutation procedure is carried out is equal to the integer part of the value of the population size multiplied by the mutation rate. These individuals are chosen randomly among the population and then the procedure is applied .The mutation rate using in this paper is 0.40.
Elitism: The elitism consists in keeping the best individual from the current population to the next one. In this paper, we take 1 as elitism value.
Population-related factors:
Population size: The GAs performance is influenced heavily by population size. Various values ranging from 20 to 200 population size were tested. Small populations run the risk of seriously under covering the solution space, a small population size causes the GAs to quickly converge on a local minimum, because it insufficiently samples the parameter space, while large populations incur severe computational penalties. According to our experience, a population size range from 50 to 200 is enough our problem. In this paper and according to our experience, we take 200 as a population size.
Initial population: It is demonstrated that a high-quality initial value obtained from another heuristic technique can help GAs find better solutions rather more quickly than it can from a random start. However, there is possible disadvantage in that the chance of premature convergence may be increased. In this paper, the initial population is simply chosen by random.
Termination criteria: It should be pointed out that there are no general termination criteria for GAs. Several heuristic criteria are employed in GAs, i.e., computing time (number of generations), no improvement for search process, or comparing the fitness of the best-so-far solution with average fitness of all the solutions. All types of termination criteria above were tried; the criterion of computing time is proven to be simple and efficient in our problem. In our experience, 200-1000 generations simulation is enough for a complicated problem as our problem (DMBP). The best results were obtained when the numbers of generations were taken as 1000 for our problem.
Problem formulation:
Assumptions: The model formulation for DMBP’s problem approach adopted in this section is based on [22]. It considers not only treatment in batch stages, which usually appears in all types of formulation, but also represents semi-continuous units that are part of the whole process (pumps, heat exchangers, others). A semi-continuous unit is defined as a continuous unit alternating idle times and normal activity periods. Besides, this formulation takes into account mid-term intermediate storage tanks, the obligatory mass balance at the intermediate storage stage, which is one of the most efficient strategies to decouple bottlenecks in batch plant design. They are just used to divide the whole process into subprocesses in order to store an amount of materials corresponding to the difference of each sub-process productivity.
This representation mode confers on the plant better flexibility for numerical resolution: It prevents the whole production process from being paralyzed by one limiting stage. So, a batch plant is finally represented as a series of batch stages (B), semi-continuous stages (SC) and storage tanks (T).
The model is based on the following assumptions:
1. The processes operate in the way of overlay.
2. Production is achieved through a series of single product campaigns.
3. Units of the same batch or semi-continuous stage have the same type and size.
4. The devices in the same production line cannot be reused by the same product.
5. The long campaign and the single product campaign are considered.
6. The type and size of parallel items in-or out-of-phase are the same in one batch stage.
7. All intermediate tanks are finite.
8. The operation between stages can be of zero wait or no intermediate tank when there is no storage.
9. There is no limitation for utility.
10. The cleaning time of the batch item can be neglected or included in processing time.
11. The size of the devices can change continuously in its own range.
Model:The model considers the synthesis of (I) products treated in (J) batch stages and (K) semi-continuous stages. Each batch stage consists of (mj) out-of-phase parallel items of the same size (Vj). Each semi-continuous stage consists of (nk) out-of-phase parallel items with the same processing rate (Rk) (i.e. treatment capacity, measured in volume unit per time unit). The item sizes (continuous variables) and equipment numbers per stage (discrete variables) are bounded. The (S-1) storage tanks, with size (Vs *), divide the whole process into (S) sub-processes.
Following the above mentioned notation, DMBP’s problem can be formulated to minimize the investment cost for all items:
The investment cost (Cost) is written as an exponential function of the unit size, is formulated in terms of the optimization variables, which represent the plant configuration:
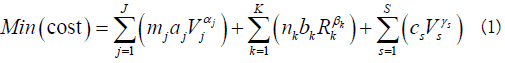
Where aj and αj, bk and βk, Cs and γs are classical cost coefficients. Equation (1) shows that there is no fixed cost coefficient for any item. This may be unrealistic and will not tend towards minimization of the equipment number per stage. Nevertheless, this information was kept unchanged in order to compare our results with those found in the literature [22].
The constraints of the problem:
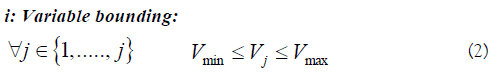
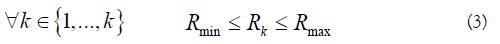
Volume Vj of the items of each batch stage j and treatment capacity Rk of each semi-continuous stage k. However, these variables are not continuous anymore and were discretized with an interval of 50 units between two possible values. This working mode was adopted in a view of realism. Indeed, since equipment manufacturers propose the items following defined size ranges, the design of operation unit equipment does not require a level of accuracy such as real number. Note, however, that the initial bounds on these size variables were kept unchanged, being for batch and semicontinuous, respectively: Vmin and Vmax, Rmin and Rmax.
Item number m
i. Time constraint: The total production time for all products must be lower than a given time horizon H:

Where Qi is the demand for product i.
ii. Constraint on productivities: the global productivity for product i (of the whole process) is equal to the lowest local productivity (of each sub-process ‘s’).
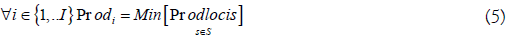
These local productivities are calculated from the following equations:
a) Local productivities for product in sub-process ‘s’:
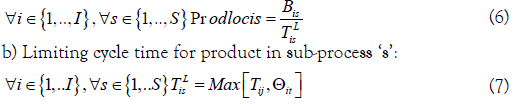
Where Js and Ks are, respectively, the sets of batch and semicontinuous stages in sub-process ‘s’.
c) Cycle time for product I in batch stage j:
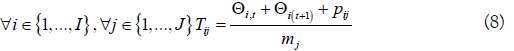
Where k and k+1 represent the semi-continuous stages before and after batch stage j.
d) Processing time of product i in batch stage j:
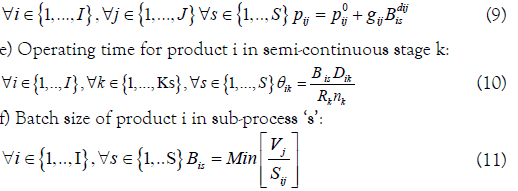
g) Finally, the size of intermediate storage tanks is estimated as the greatest size difference between the batches treated in two successive sub-processes:
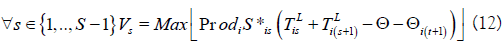
Process description
The case study is a multiproduct batch plant for the production of proteins taken from the literature [3]. This example is used as a test bench since short-cut models describing the unit operations involved in the process. The batch plant involves eight stages for producing four recombinant proteins, on one hand, two therapeutic proteins, human insulin (A) and vaccine for hepatitis (B) and, on the other hand, a food grade protein, chymosin (C), and a detergent enzyme, cryophilic protease (D). As illustrate in Figure 3, the flow sheet of the multiproduct batch plant considered in this study. All the proteins are produced as cells grow in the fermenter.
Figure 3: Multiproduct batch plant for protein production.
Vaccines and protease are considered to be intracellular: the first micro filter 1 is used to concentrate the cell suspension, which is then sent to the homogenizer for micro filter 2 is used to remove the cell debris from the solution proteins.
The ultrafiltration 1 step is designed to concentrate the solution in order to minimize the extractor volume. In the liquid–liquid extractor, salt concentration (NaCl) is used solution in order to minimize the extractor volume. In the liquid–liquid extractor, salt concentration (NaCl) is used to first drive the product to a poly-ethylene-glycol (PEG) phase and again into an aqueous saline solution in the back extraction. Ultrafiltration 2 is used again to concentrate the solution. The last stage is finally chromatography, during which selective binding is used to better separate the product of interest from the other proteins. Insulin and chymosin are extracellular products. Proteins are separated from the cells in the first micro filter 1, where cells and some of the supernatant liquid stay behind. To reduce the amount of valuable products lost in the retentate, extra water is added to the cell suspension. The homogenizer and micro filter 2 for cell debris removal are not used when the product is extracellular. Nevertheless, the ultra-filter 1 is necessary to concentrate the dilute solution prior to extraction. The final step of extraction, ultrafiltration 2 and chromatography are common to both the extracellular and intracellular products.
On the other hand, the Figure 1 shows the allocation of intermediate storage tanks. Three tanks have been selected: the first after the fermenter, the second after the first ultra-filter, and the third after the second ultra-filter.
The typical results obtained by GAs were run 30 times starting from random initial population guarantees the stochastic nature of the algorithms with demand modeled by Gaussian probability distribution, minimizing the cost plant. The results are developed as shown in Table 1: Plant Cost, Hi and CPU time. Neverthless, the structure of equipment was illustrated in Table 2.
| Min (Cost plant) | % Std.Dev | Hi | CPU time |
|---|---|---|---|
| 833.647 [$] | 0.50% | 5,491.123159 (h) | <1(s)* |
Note: *CPU time was calculated to this method on Microsoft Windows XP Profesional Intel(R)D CPU 2.80 Ghz, 2.99 GB of RAM.
Table 1: Results obtained by GAs.
| Stage | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Vi | 22.6085 | 6.7988 | 1.0794 | 1.6191 | 9.0651 | 0.8151 | 0.5497 | 0.0754 |
| Rk | 14.8047 | 1.004 | 7.9194 | 99.888 | 16.275 | |||
| Vs | 27.141 | 2.0241 | 0.3467 | |||||
| mi | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| nk | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Table 2: Equipment structure.
The total production time computed by GAs is 5,491.12h to fulfill the eventual increase of future demand caused by market fluctuations. The table showed also a very small Std. Dev (error). In addition, GAs results in a faster convergence (less than one second).
On the other hand, the GAs allows the reduction of the idle time to the stage. Table 3 shows the idle times obtained by GAs. From these results, we can see that the results obtained by GAs are power.
| Unit | ||||||||
|---|---|---|---|---|---|---|---|---|
| Product | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Insulin | 0 | 0 | 0 | 0.01 | 0 | 0 | ||
| Vaccine | 0 | 1.93 | 0.04 | 0 | 2.91 | 0 | 0.17 | 0 |
| Chymosin | 0 | 0.01 | 0 | 0 | 0.31 | 0.17 | ||
| Protease | 0 | 2.09 | 0 | 0 | 3.07 | 0 | 0.5 | 0 |
Table 3: Idle Times in Plant with Parallel Units and Intermediate Storage Tanks by GAs.
However, since the case study has been taken from Montagna et al. [23], they solved the problem using rigorous mathematical programming (MINLP) which is solved to global optimality (minimize the capital cost $829,500) with implementation of the outer approximation/equality relaxation/augmented penalty method. However in previous work, they didn’t mentioned anything about CPU time, also in their model, they didn’t take into account operation costs. Nonetheless, their model needed a long computational time and require severe initial values to the optimization variables. Montagna et al. also showed in their paper that the behavior of the demand was completely deterministic. However, this assumption does not seem to be always a reliable representation of the reality, since in practice the demand of pharmaceutical products resulting from the batch industry is usually changeable (Table 4).
| Crossover type | Average of the runs2 | Geometric mean of the runs3 | ||||
|---|---|---|---|---|---|---|
| Pc=0.6 | Pc=0.8 | Pc=1.0 | Pc=0.6 | Pc=0.8 | Pc=1.0 | |
| 1-point | 0.515 | 0.583 | 0.379 | 0.401 | 6.81E-2 | 2.33E-2 |
| 2-point | 0.216 | 0.753 | 0.474 | 1.28E-2 | 5.02E-3 | 3.13E-3 |
| uniform | 0.113 | 0.183 | 0.203 | 9.52E-2 | 6.14E-3 | 3.17E-2 |
| NN-2-point | 0.553 | 0.277 | 0.927 | 3.35E-2 | 7.90E-4 | 7.01E-4 |
| NN-uniform | 0.376 | 0.305 | 0.299 | 3.47E-4 | 8.50E-5 | 9.12E-6 |
Note: 2The arithmetic mean is calculated as 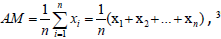 , 3The geometric mean is calculated as
, 3The geometric mean is calculated as 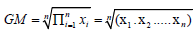
Table 4: Simulation results of multiproduct batch plant problem after 1000 generations.
GAs performed effectively and gave a solution within 0.5% of the global optimal 833,647.5[$], GAs provided also interesting solutions, in terms of quality as well as of computational time.
Furthermore, GAs results in a faster convergence. However, GAs is designed to deal with problems of a more complicated as our problem, DMBP, successfully and the computing time (<1s) is less than MINLP.
These results are important, because they demonstrate the effectiveness of GAs in solving the complicated design problem of DMBP, which is due to GAs searching from population (not a single point), and its parallel computing nature and can be applied to deal with uncertain demand.
Now, some observation about some important aspects in our implication of GAs and some problems in practice: The most important of all is the method of coding, because the codification is a very important issue when a genetic algorithm is designed to deal with the combinatorial problem, as well as also the characteristics and inner structure of the DMBP.
The commonly adopter concatenated, multiparameter, mapped, fixed point coding are not effective in searching to the global optimum [23]. According to the inner structure of the design problem of multiproduct batch that gives us some clues for designing the above mixed continuous discrete coding method with a four-point crossover operator. As it is evident to the results of application, this coding method is well fitted to the proposed problem.
Another aspect that affects the effectiveness of our Genetic Algorithms procedure considerably is a crossover.
Corresponding to the proposed coding method, we adopted a fourpoint crossover. It is commonly believed that multipoint crossover is more effective than the traditional one point crossover method. It is also important to note that the selection of crossover points as well as the way to carry out the crossover should take into account the bit string structure, as it is the case in our codification [24-27].
A problem in practice is the premature loss of diversity in the population, which results in premature convergence. Because premature convergence is so often the case in the implementation of GAs according to our calculation experience. Our experience makes it clear that the Elitism parameter can solve the premature problem effectively and conveniently.
We applied Genetic Algorithms with an effective mixed continues discrete coding method with a four crossover point to solve the problem of DMBP. GAs performed effectively and gave a solution within 0.5% of the global optimum.
GAs with mixed continuous discrete coding with a four-point crossover is well fitted for the proposed optimization problem and demonstrates the following advantages in application:
• GAs has no special demand for initial values of decision variables. The initial population of strings is chosen randomly as long as it does not violate the constraints for the problem.
• As is evident from the computation results, GAs yield highly satisfactory global optimum.
• Due to the parallel computing nature GAs result in faster convergence in comparison with MINLP.
• GAs are simple in structure and are convenient for implementation, with no more complicated mathematical calculation than such simple operators as encoding , decoding, testing constraints, and computing values of objective.
• In this framework, the GAs with an effective mixed continuous discrete coding method with a four point crossover operator gave us the high efficiency and justifies its factibility use for solving non-linear mathematical models with the uncertainties parameters.
• Finally, this framework provides an interesting decision/ making approach to improve design multiproduct batch plants under conflicting goals.
Citation: El-Hamzaoui Y (2021) Optimization of Operating Conditions for Protein Production Plants using Mixed Integer Nonlinear Programming and Genetic Algorithms. Drug Des. 10:176.
Received: 25-Jan-2021 Accepted: 08-Feb-2021 Published: 15-Feb-2021 , DOI: 10.35248/2169-0138.21.10.176
Copyright: © 2021 El-Hamzaoui Y. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.