Journal of Nutrition & Food Sciences
Open Access
ISSN: 2155-9600
ISSN: 2155-9600
Review Article - (2015) Volume 0, Issue 0
The diet problem is a classic problem, one among the earliest problems formulated as a linear programming. The goal of the diet problem is to select a set of nutrients that will satisfy a set of daily nutritional requirement at minimum cost. Poultry being simple stomached species, cannot synthesize most of the nutrients required for them and so the nutrients become dietary essentials. Chicken has to be fed adequate quantities of balanced diet for its growth, livability and to exhibit its genetic potential to the full extent. Maximizing live bird profitability is similar to minimizing feed cost per kg live weight. The nutrient diet model formulation is a combination of different feed ingredients needed for a balance diet of the bird. The generic mathematical model which is applicable to each type of ration nine decision variables and ten parameters is constructed as subject to a set of twelve obtained constraints from a local farm. The model was solved using an excel solver package for easy accessibility. Model solution and post-optimality test results were obtained and compared with existing practice of the case study farm. The proposed optimal formulation of the linear programming model gives about 7.48% and 9.96% reduction in feed formulation costs compared to the existing formulation in case of broiler starter and finisher respectively on the farm. The model also reduced the amount of fat contained in the existing ration but adding more flesh by significantly increased the metabolisable energy needed for physiological structure. Post-optimality test or Sensitivity analysis also gave useful insight into the impact of changes in costs of feed inputs.
Keywords: Broiler rations or feed, Nutrient diet, Formulation, Linear programming; Post-optimality test
Feed is a major component of the total cost of broiler production [1]. Broiler rations should be formulated to supply the correct balance of energy, protein and amino acids, minerals, vitamins and essential fatty acids to allow optimum growth and performance. It is widely accepted that the choice of dietary nutrient levels should be an economic decision to be made for each company or enterprise. Maximizing live bird profitability is similar to minimizing feed cost per kg live weight [1]. Linear programming will enable us to make a productive decision in optimizing nutrient diet required of broiler at minimal cost, bearable risk and optimum satisfaction of minimum requirements of each diet nutrient types per day.
As the feed cost represents an expensive input (70-80% of broiler production cost), the poultry producer should be aware of the dynamics of the feed in its influence on final product quantity and quality [2].
Formulating feed ideally requires in-depth knowledge of several parameters such as the energy level to be maintained in the diet, balancing the amino acid profile and electrolytes of feed etc., which, otherwise, if not properly monitored, could negatively influence the performance and profitability of the business.
Further, in light of environmental challenges and disease outbreaks, it is even more challenging to extract the total genetic capability of the birds [2].
Nutritionists should look at several critical parameters whilst formulating broiler feed. Important amongst these are:
• Nutritive value of raw materials
• Amino acid digestibility
• Amino acid and calorie ratio
• Selection of suitable fat source
• Calcium requirement of birds
• Electrolyte balancing
• Immuno-modulation
• Summer management
Poultry feed is composed of 60-65% Energy giving materials, 30-35% of Protein source, 2-8% Minerals source. And above all water, which is considered as the principal nutrient should be pure, wholesome, and free from physical impurities, toxic substances and bacterial contamination. The poultry contribute a good quota to Nigeria economy and employment opportunities creation [3-5]. It is therefore important that poultry farming be carried out efficiently for high productivity and sustainability of the industry in Nigeria. It has been established that feeding constitutes over 70% of the total cost of egg and broiler production [6], which implies that efforts to increase poultry industry productivity should be directed towards improving feed formulation system. This paper seeks to apply mathematical optimization techniques using excel solver due to its availability to the feed formulation problem of a typical Nigerian poultry farm using locally available feed ingredients.
Some of the common techniques employed in feed formulation include The Pearson Square method, Linear Programming, Non Linear Programming, and Trial and Error method. Linear programming is the common method of Least Cost Feed Formulation which compares the nutrients required by the animal to the nutrients supplied by the available feed ingredients, and combines them to obtain a balanced diet at the least possible cost. [4]
Broiler rations feedstuffs and nutrients
Poultry diets are made primarily from a mixture of several feedstuffs such as cereal grains, soybean meal, animal by-product meals, fats, and vitamin and mineral premixes [7,8]. A poultry diet is expected to contain three essential nutrients of protein, vitamins, and minerals as well as provides adequate metabolisable energy (ME). Energy is very critical in poultry feed, in fact, the more the energy loaded in the ration, the less feed the birds would consume [9]. The most easily available sources of energy are the carbohydrates contained in common grains, grain byproducts and plants generally. Most of the carbohydrate in poultry diets is provided by cereal grains. Suitable quantities of fat may be added to increase dietary energy concentrations and palatability.
The nutrient diet model formulation is a combination of different feed ingredients needed for a balance diet of the bird. The model has to satisfy a set of constraints on nutritional levels, availability restrictions, special ingredients to be included, demand constraint, energy and budget constraints. The generic mathematical model which is applicable to each type of ration using the available ingredients is constructed as follows:
Notations:
Let i = feed nutrient components with i = 1,2,...m
j = feed ingredients with j =1, 2…n
Xj = quantity of feed ingredient j in the feed mix (decision variable)
N = total quantity (Kg) of feed to be produced
Z = Total cost of feed ingredients used in the feed formulation
Cj = unit cost of feed ingredient j
aij= amount (in fraction of Xj ) of nutrient i available in feed ingredient j
bi = dietary requirement (fraction of N) of nutrient i for a bird category
Objective function
The specified LP model for the attainment of the objective function is:
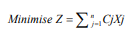
Subject to:
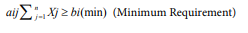
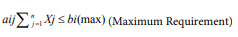

Xj=0 (Non – Negativity constraints)
Assumptions of linear programming
Before a valid result can be obtained from linear programming technique, the following assumptions must be held:
• Linearity: There must be a linear relationship between the output and the total quantity of each resource consumed. If the objective function is not linear, the technique will not be applicable.
• Simple objective: The objective can either be maximization or minimization of one activity.
• Certainty: All values and quantities must be known with certainty.
• Additivity: This means that the sum of resources used by different activities must be equal to the total quantity of the resources used by each activity for all the resources.
• Divisibility: Perfect divisibility of outputs and resources must exist.
• Non-negativity: Decision variables cannot be added to the final objective function in a negative way. That is each of the decision variables must either be positive or zero.
• Finiteness: The constraints and the variables must be finite so that it can be programmed. Hence, a finite number of activities and constraints must be employed.
• Proportionality: This implies that the contribution of each variable to the final objective function is directly proportional to each variable. If we want to double the output then all decision variables must be doubled [10,11].
Mathematical models were constructed for starter and finisher types of broiler ration using limited ingredients. The objective of the models was to minimize cost of producing a particular diet after satisfying a set of constraints. These constraints were mainly those from nutrient requirements of each bird and ingredient constraints. The variables in the models were the ingredients while the cost of each ingredient and the nutrient value of each ingredient was the parameter. The main source of data collection about feedstuffs specifications, constraints imposed on the selected feedstuffs and the dietary nutrient requirements for broilers. Costs of feedstuffs used in the diet formulation were obtained from the prevailing market prices of feedstuffs in Nigeria through survey. The analysis of feed ingredients and minimum and maximum levels of various feedstuffs used in diet obtained from standard tables and sources [1]. It recommended nutritional and restriction levels of the Metabolizable Energy (ME), protein, limiting amino acids, calcium, phosphorus, fiber and fat will be adopted in this study. The most popular feedstuffs used in ration formulation for local farms and broiler feed factories include yellow corn(maize), soybean, fish meal, premix, vitamin/mineral, salt, lysine, oyster shell, bone meal, methionine, wheat bran and calcium diphosphate. These feedstuffs were used in this study.
Model construction
The linear programming model for broiler starter ration is:
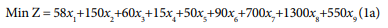
Subject to:
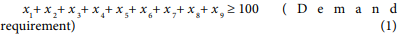
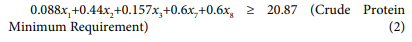
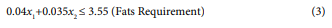
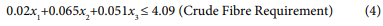
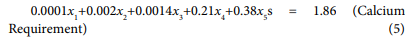
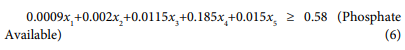
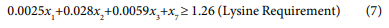
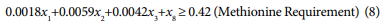




The linear programming model for broiler finisher ration is:
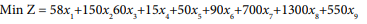
Subject to:
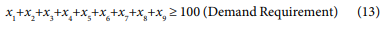
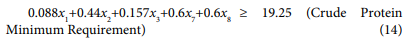

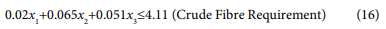
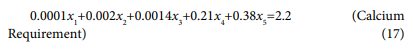
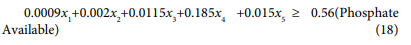
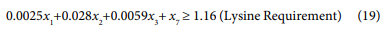
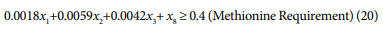



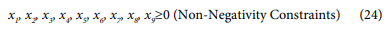
The proposed model was solved using a general excel solver package due to its accessibility by common farmers in Nigeria to easily use for optimum nutrients combination and improved performance of their birds. Tables 1-8 highlighted the comparison between the existing formulations with the proposed optimal formulation.
Existing and Proposed ration formulation for starter broiler
| Ingredients | Costs (₦/kg) | Crude Protein % | Fats % | Crude Fibre% | Ca% | P, % | Lysine % | Methionine % | ME (Kcal/kg) |
|---|---|---|---|---|---|---|---|---|---|
| Maize, x1 | 58 | 8.8 | 4.0 | 2.0 | 0.01 | 0.09 | 0.25 | 0.18 | 3432 |
| Soyabean, x2 | 150 | 44 | 3.5 | 6.5 | 0.2 | 0.2 | 2.8 | 0.59 | 2230 |
| Wheat bran, x3 | 60 | 15.7 | - | 5.1 | 0.14 | 1.15 | 0.59 | 0.42 | 1300 |
| Oyster shell, x4 | 15 | - | - | - | 21 | 18.5 | - | - | - |
| Bone meal, x5 | 50 | - | - | - | 38 | 1.5 | - | - | - |
| Table salt, x6 | 90 | - | - | - | - | - | - | - | - |
| Lysine, x7 | 700 | 60 | - | - | - | - | 100 | - | - |
| Methionine, x8 | 1300 | 60 | - | - | - | - | - | 100 | - |
| Broiler premix, x9 | 550 | - | - | - | - | - | - | - | - |
Table 1: Cost implications of feedstuffs and nutrient levels of feed ingredients (NRC Source).
| Parameter | Starter Ration | Finisher Ration |
|---|---|---|
| Crude Protein (kg) | 20.87 | 19.25 |
| Fats (kg) | 3.55 | 3.51 |
| Available Phosphate (kg) | 0.58 | 0.56 |
| Lysine (kg) | 1.26 | 1.16 |
| Crude Fibre (kg) | 4.09 | 4.11 |
| Calcium (kg) | 1.86 | 2.20 |
| Methionine (kg) | 0.42 | 0.40 |
| Metabolizable Energy (Kcal/kg) | 2826.39 | 2766.67 |
| Salt (kg) | 0.3 | 0.3 |
| Premix (kg) | 0.3 | 0.3 |
| Weight (kg) | 100 | 100 |
Table 2: Formulation restrictions on nutrients and feedstuffs for broiler rations by typical Nigerian feed mill.
| Decision Variables | Objective Coefficient | Existing ration formulation | Proposed optimal ration formulation | ||
|---|---|---|---|---|---|
| Ingredients | Cost (₦/kg) | Quantity (kg) | Cost (₦) | Quantity (kg) | Cost (₦) |
| Maize, x1 | 58 | 50 | 2900 | 31.27 | 1813.66 |
| Soyabean, x2 | 150 | 35 | 5250 | 30.52 | 4578 |
| Wheat bran, x3 | 60 | 10 | 600 | 29.03 | 1741.8 |
| Oyster shell, x4 | 15 | 3 | 45 | 8.36 | 125.4 |
| Bone meal, x5 | 50 | 2 | 100 | 0.00 | 0 |
| Salt, x6 | 90 | 0.3 | 27 | 0.30 | 27 |
| Lysine, x7 | 700 | 0.1 | 70 | 0.16 | 112 |
| Methionine, x8 | 1300 | 0.1 | 130 | 0.06 | 78 |
| Broiler premix, x9 | 550 | 0.3 | 165 | 0.30 | 165 |
| Total | 100 | 9, 287 | 100 | 8, 640.86 | |
Table 3: Existing and Proposed ration formulation for starter broiler.
| Reduced | Objective | Allowable | Allowable | ||||
|---|---|---|---|---|---|---|---|
| Cell | Name | Value | Cost | Coefficient | Increase | Decrease | |
| $B$20 | SOLUTION X1:Maize | 31.27 | 0.00 | 58 | 169.6297923 | 21.16223288 | |
| $C$20 | SOLUTION X2:Soya beans | 30.52 | 0.00 | 150 | 202.4343262 | 75.0904473 | |
| $D$20 | SOLUTION X3:Wheat bran | 29.03 | 0.00 | 60 | 16.8971673 | 116.1742835 | |
| $E$20 | SOLUTION X4:Oyster shell | 8.36 | 0.00 | 15 | 31.73785688 | 3832.568681 | |
| $F$20 | SOLUTION X5:Bone meal | 0.00 | 57.34 | 50 | 1E+30 | 57.34035672 | |
| $G$20 | SOLUTION X6:Salt | 0.30 | 0.00 | 90 | 1E+30 | 1E+30 | |
| $H$20 | SOLUTION X7:Lysine | 0.16 | 0.00 | 700 | 3650.304956 | 448.1822994 | |
| $I$20 | SOLUTION X8:Methionine | 0.06 | 0.00 | 1300 | 120829.4719 | 1067.903732 | |
| $J$20 | SOLUTION X9:Premix | 0.30 | 0.00 | 550 | 1E+30 | 1E+30 | |
| Constraints | |||||||
| Final | Shadow | Constraint | Allowable | Allowable | |||
| Cell | Name | Value | Price | R.H. Side | Increase | Decrease | |
| $K$8 | DEMAND LHS | 100 | 42.59691125 | 100 | 22.04010174 | 20.13307524 | |
| $K$9 | SALT LHS | 0.3 | 47.40308875 | 0.3 | 20.13307524 | 0.3 | |
| $K$10 | PREMIX LHS | 0.3 | 507.4030888 | 0.3 | 20.13307524 | 0.3 | |
| $K$11 | CALCIUM LHS | 1.86 | -131.4138631 | 1.86 | 4.227945799 | 1.554450857 | |
| $K$12 | FATS LHS | 2.319015507 | 0 | 3.55 | 1E+30 | 1.230984493 | |
| $K$13 | CRUDE FIBRE LHS | 4.09 | -760.5812226 | 4.09 | 0.856886702 | 0.645018371 | |
| $K$14 | PHOSPHATE LHS | 1.969306265 | 0 | 0.58 | 1.389306265 | 1E+30 | |
| $K$15 | LYSINE LHS | 1.26 | 469.7115319 | 1.26 | 11.2924083 | 0.148780339 | |
| $K$16 | METHIONINE LHS | 0.42 | 1069.711532 | 0.42 | 11.2924083 | 0.06159284 | |
| $K$17 | MET. ENERGY LHS | 213122.3821 | 0 | 2826.39 | 210295.9921 | 1E+30 | |
| $K$18 | CRUDE PROT. LHS | 20.87 | 312.8192614 | 20.87 | 1.81952375 | 7.326496438 | |
Table 4: Sensitivity analysis of the proposed optimal formulation ration for starter.
| Chemical composition of ration | Existing ration formulation | Proposed optimal ration formulation |
|---|---|---|
| Crude Protein | 20.87 | 20.87 |
| Fats | 3.55 | 2.32 |
| Available Phosphate | 0.58 | 1.97 |
| Lysine | 1.26 | 1.26 |
| Crude Fibre | 4.09 | 4.09 |
| Calcium | 1.86 | 1.86 |
| Methionine | 0.42 | 0.42 |
| Metabolizable Energy | 2,826.39 | 213,122.4 |
| Cost | ₦ 9, 287 | ₦ 8, 640.86 |
Table 5: Chemical composition of Existing and Proposed ration formulation for starter broiler.
| Decision Variables | Objective Coefficient | Existing ration formulation | Proposed optimal ration formulation | ||
|---|---|---|---|---|---|
| Ingredients | Cost (₦/kg) | Quantity (kg) | Cost (₦) | Quantity (kg) | Cost (₦) |
| Maize, x1 | 58 | 50 | 2900 | 25.09 | 1455.22 |
| Soyabean, x2 | 150 | 30 | 4500 | 24.16 | 3624 |
| Wheat bran, x3 | 60 | 14 | 840 | 39.95 | 2397 |
| Oyster shell, x4 | 15 | 4 | 60 | 9.97 | 149.55 |
| Bone meal, x5 | 50 | 2 | 100 | 0.00 | 0 |
| Salt, x6 | 90 | 0.3 | 27 | 0.30 | 27 |
| Lysine, x7 | 700 | 0.1 | 70 | 0.18 | 126 |
| Methionine, x8 | 1300 | 0.1 | 130 | 0.04 | 52 |
| Broiler premix, x9 | 550 | 0.3 | 165 | 0.30 | 165 |
| Total | 100 | 8, 792 | 100 | 7, 995.77 | |
Table 6: Existing and Proposed ration formulation for finisher broiler.
| Final | Reduced | Objective | Allowable | Allowable | |||
|---|---|---|---|---|---|---|---|
| Cell | Name | Value | Cost | Coefficient | Increase | Decrease | |
| $B$20 | SOLUTION X1:Maize | 25.09 | 0.00 | 58 | 169.6297923 | 21.16223288 | |
| $C$20 | SOLUTION X2:Soya beans | 24.16 | 0.00 | 150 | 202.4343262 | 75.0904473 | |
| $D$20 | SOLUTION X3:Wheat bran | 39.95 | 0.00 | 60 | 16.8971673 | 116.1742835 | |
| $E$20 | SOLUTION X4:Oyster shell | 9.97 | 0.00 | 15 | 31.73785688 | 3832.568681 | |
| $F$20 | SOLUTION X5:Bone meal | 0.00 | 57.34 | 50 | 1E+30 | 57.34035672 | |
| $G$20 | SOLUTION X6:Salt | 0.30 | 0.00 | 90 | 1E+30 | 1E+30 | |
| $H$20 | SOLUTION X7:Lysine | 0.18 | 0.00 | 700 | 3650.304956 | 448.1822994 | |
| $I$20 | SOLUTION X8:Methionine | 0.04 | 0.00 | 1300 | 120829.4719 | 1067.903732 | |
| $J$20 | SOLUTION X9:Premix | 0.30 | 0.00 | 550 | 1E+30 | 1E+30 | |
| Constraints | |||||||
| Final | Shadow | Constraint | Allowable | Allowable | |||
| Cell | Name | Value | Price | R.H. Side | Increase | Decrease | |
| $K$8 | DEMAND LHS | 100 | 42.59691125 | 100 | 29.73687182 | 16.15136586 | |
| $K$9 | SALT LHS | 0.3 | 47.40308875 | 0.3 | 16.15136586 | 0.3 | |
| $K$10 | PREMIX LHS | 0.3 | 507.4030888 | 0.3 | 16.15136586 | 0.3 | |
| $K$11 | CALCIUM LHS | 2.2 | -131.4138631 | 2.2 | 3.39178683 | 2.030084858 | |
| $K$12 | FATS LHS | 1.84913525 | 0 | 3.51 | 1E+30 | 1.66086475 | |
| $K$13 | CRUDE FIBRE LHS | 4.11 | -760.5812226 | 4.11 | 0.61767965 | 0.887621745 | |
| $K$14 | PHOSPHATE LHS | 2.37440899 | 0 | 0.56 | 1.81440899 | 1E+30 | |
| $K$15 | LYSINE LHS | 1.16 | 469.7115319 | 1.16 | 9.059113711 | 0.176494031 | |
| $K$16 | METHIONINE LHS | 0.4 | 1069.711532 | 0.4 | 9.059113711 | 0.044398686 | |
| $K$17 | MET. ENERGY LHS | 191917.2968 | 0 | 2766.67 | 189150.6268 | 1E+30 | |
| $K$18 | CRUDE PROT. LHS | 19.25 | 312.8192614 | 19.25 | 2.158451067 | 5.800384248 | |
Table 7: Sensitivity analysis of the proposed optimal formulation ration for finisher.
| Chemical composition of ration | Existing ration formulation | Proposed optimal ration formulation |
|---|---|---|
| Crude Protein | 19.25 | 19.25 |
| Fats | 3.51 | 1.85 |
| Available Phosphate | 0.56 | 2.37 |
| Lysine | 1.16 | 1.16 |
| Crude Fibre | 4.11 | 4.11 |
| Calcium | 2.20 | 2.20 |
| Methionine | 0.40 | 0.40 |
| Metabolizable Energy | 2,766.67 | 191,917.3 |
| Cost | ₦ 8, 792 | ₦ 7, 995.77 |
Table 8: Chemical composition of Existing and Proposed ration formulation for finisher broiler.
The proposed optimal ration formulation results produced by linear programming model showed that the starter ration consists of 31.27 kg maize (yellow), 30.52 kg soyabean, 29.03 kg wheat bran, 8.36 kg Oyster shell, 0.16 kg lysine, 0.06 kg methoinine, 0.3 kg Salt, and 0.3 kg premix mix is the proposed optimal ration for starter broilers according to the local feedstuffs availability. This ration meets all the nutritional requirements needed for starter broiler. The cost of the ration is around ₦ 8,640.86 as against the existing formulation cost of ₦ 9,287. This cost saves about ₦ 646.14, which is about 7.48% and quite significant when considered at a larger capacity. Obviously feed formulation is more cost effective when based on valid mathematical programming.
It can be observed that the shadow prices of the surplus resources (fat, metabolizable energy and phosphate) are zero. Which implies that there is no economic advantage in allocating more of that resource, while a unit increase in the other resources will lead to a corresponding increase in the objective value to the tune of the shadow price. For instance, a unit increase in the total quantity of feed produced will increase the objective value by ₦ 42.59 within the allowable increase and decrease.
Existing and proposed ration formulation for finisher broiler
Also, the proposed optimal ration formulation results produced by linear programming model in the case of the finisher ration consists of 25.09 kg maize (yellow), 24.16 kg soyabean, 39.95 kg wheat bran, 9.97 kg Oyster shell, 0.18 kg lysine, 0.04 kg methoinine, 0.3 kg Salt, and 0.3 kg premix mix is the proposed optimal ration for finisher broilers according to the local feedstuffs availability. This ration meets all the nutritional requirements needed for finisher broiler. The cost of the ration is around ₦ 7,995.77 as against the existing formulation cost of ₦ 8,792. This cost saves about ₦ 796.23, which is about 9.96% and quite significant when considered at a larger capacity. This is also cost effective when based on valid mathematical programming.
It can be observed that the shadow prices of the surplus resources (fat, metabolizable energy and phosphate) are zero. Which implies that there is no economic advantage in allocating more of that resource, while a unit increase in the other resources will lead to a corresponding increase in the objective value to the tune of the shadow price. For instance, a unit increase in the total quantity of feed produced will increase the objective value by ₦42.59 within the allowable increase and decrease.
This sort of proposed optimal model after looking at the optimum solution to determine its reasonableness and implementability and even solving the modified model is typical in practical applications of optimization. This model has reduced the amount of fat contained in the existing ration but adding more flesh by significantly increased the metabolizable energy needed for physiological structure. The model has also achieved the study objective by minimizing the total production cost of the diet ration and made it accessible to an average Nigerian farmers by making use of a common excel package.
The proposed optimal model is flexible and can be modified by including additional constraints to make sure that the solution obtained is economical and adequate for starter and finisher broiler birds. Further works are hereby recommended to be done in the area of modification of the model to include substantive natural ingredients to substitute some of the costly ingredients like lysine, methionine and premix, which will as well serve the same nutritive purpose.