For decades, scientists have contemplated possible roles of water in biological processes beyond those normally associated with its solvent properties or as a medium for biochemical reactions. Alternative thinking, including the role for water in the regulation of biological phenomena, recently reviewed by Drozdov and Nagorskaya [1], have emerged to suggest that dynamics of molecular interactions in water under the action of external electromagnetic fields may more directly impact cell and macromolecule function. However, most still doubt that there is a fundamental role for the structure of water in living systems. This skepticism is based primarily on the classical thermodynamic approach when applied to the role of water in biology. The basic premise is that the state of water cannot change or be changed by an external influence, the energy of which is substantially lower than the thermal energy of the system (the kT problem) [1].

Previous studies have reported evidence that properties inherent in the structure of water relate to phenomenon of biological rhythms as an underlying the mechanism responsible for the characteristic periodic oscillations [2]. For such mechanisms to be oscillatory, transitions between different states of water must first of all be synchronous. This requirement would extend to observed coherent water structures, some of which appear to extend over relative long distances [3,4].

As has been noted by several investigators working independently, the idea of coherent spin conversions between ortho and para water molecules as playing a fundamental role in biological oscillations have only recently come to the forefront [1,2,5-8]. Consistent with this idea is the concept that water is a mixture of two distinct liquids, each consisting of predominantly ortho or para water molecules, respectively [9]. Subsequent studies have provided evidence of orthopara interconversions [7,10-12] evidence published subsequent to the report of Tikhonov and Volkov [13] where equilibrium of pure ortho water vapor require 4 h to approach a 3:1 ratio of ortho to para water and appeared to oscillate with a period length of about 18 min in doing so. FTIR measurements of ortho-H₂O/Para H₂O interconversions were carried out in the middle infra-red spectral region above a water sample surface [5]. Determinations at 3801 and 2779 cm^-1 respectively, where analyzed by decomposition fits using an imposed period length of 18 min revealed a repeating pattern of oscillations similar to that associated with the cellular biological lock [2,14,15]. Recurrent maxima, two of which ? and ? were separated by about 6 min and two additional maxima ? and ? separated from each other and from maxima ? and ? by 4 min were observed. A similar pattern of oscillations was observed for the luminescence intensity of aqueous solutions [7]. In this report, oscillations in the luminescence of water collected at 1 sec intervals were analyzed with findings consistent with the use of measurements of water luminescence as a means to monitor synchronized oscillations in the energy levels exhibited by pure water which may be attributed to ortho-para spin pair interconversions.

Irradiation

Samples were treated as described by Gudkov et al. [7]. Distilled water (10 mL; electrical conductivity 120 μS/m, pH 5.6) in a 20 mL polypropylene vial for liquid scintillation counting (Beckman, United States) was irradiated in the dark at room temperature with a 5 mW diode laser through the open surface by a quartz light guide. The distance from the light guide end to the water surface was about 10 mm, and the mean density of the light flux on the water surface was 1 mW/cm².

Measurement of luminescence

A vial with an irradiated sample was placed in a Biotoks-7AM (Ekon, Russia) high-sensitivity chemiluminometer operating in the regime of a photon counter with a sensitivity band at 380-710 nm. The time of signal accumulation and the periodicity of recording the data was 1 sec. The efficiency of photon counting was about 10%, as determined by calibration against Cherenkov radiation from isotope 32P. The region of the luminescence spectrum was estimated using blue or red optical filters with 99% transmission of light flow at 380-520 and 590-800 nm, respectively. In experiments with radiation at the wave length λ=1264 nm, at least 5 experimental series were analyzed and the series themselves contained at least 15000 points.

Results of forward averaged data were analyzed using fast Fourier transform and decomposition fits [16] to verify the reproducibility of the signals. To determine the period length the fast Fourier transforms were performed by means of a user-defined transform in MATLAB 2014. Decomposition fits were used to predict patterns based on the period length determined from Fourier analysis. The decomposition fits used Minitab 17, a statistical package. Three measured values were used to evaluate accuracy: average percentage error (MAPE), as a measure of the periodic oscillation, mean average deviation (MAD), as a measure of the absolute average deviations from the fitted values, and mean standard deviation (MSD), as the measure of standard deviation from the fitted values plus R2 and the Henriksson-Merton p value [16].

MATLAB computational software was used to determine the number of oscillations in a given data set. The computational script calculates the sample average in order to normalize the data and then utilizes a sorting algorithm to count all distinct maxima greater than the average.

Analysis of water luminescence collected at 1 sec intervals revealed a persistent dynamic of change in the form of sequential fluctuations in signal amplitude. T-test comparison of two different data sets performed with Minitab 17 indicated no statistically significant difference in the data (p<0.05). Measurements between 100 and 800 sec from a single data set were selected for detailed evaluation. Histograms of the data conform to a normal distribution, suggesting that any noise present is fully random and can be accounted for during Fourier analysis.

Luminescence data were subjected to a moving average (Figure 1).

Figure 1: >Moving average of data collected at 1 sec intervals over 2.4 × 10⁴ sec according to the formula

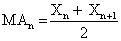
Where MA is the moving average sequence, X is a raw data set, and n is the entry index. T-tests between a raw set and its moving average show a lack of differences (p<0.05), suggesting no loss of inherent data upon smoothing.

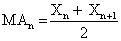
Where MA is the moving average sequence, X is a raw data set, and n is the entry index. T-tests between a raw set and its moving average show a lack of differences (p<0.05), suggesting no loss of inherent data upon smoothing (Figure 2).

Figure 2: Fourier analysis of data of Figure 2 indicative of two periods one 1130 sec=18.8 min at 0.000885 Hz and one at 288 sec=4.8 min at 0.0035 Hz.

Apparent from analyses of the moving average was a repeating pattern of sinusoidal segments shown by Fast Fourier analysis to have a signal at 0.000885 Hz corresponding to a period length of 1130 sec or 18.8 min. A ca. 18.8 min period is evident as well from the decomposition fit of the data of Figure 1 shown in Figure 3. Within each 18.8 min period was a recurring non-sinusoidal pattern of approximately 4 maxima corresponding to the Fourier signal at 0.0035 Hz average period length of 286 sec (4.8 min) (Figure 2). Decomposition fits revealed within each 18.8 min period four unevenly spaced maxima two of which, labeled ? and ?, were separated by 6 min and two of which (? and ?) were separated from each other and maxima ? and ? by about 4 min [6 min+3 (4 min)=18 min]. Each 18.8 min segment was composed of 198 ± 9 discernable maxima with a fundamental oscillation of about 6 sec (5.5 to 6 sec, ave 5.7 sec). In these analyses, average maximum and minimum values remained more or less more constant throughout the data set. T-tests on Fast Fourier Transforms from two independent data sets showed a lack of statistical difference (Figure 4).

Figure 3: Decomposition fit (light grey) of data of Figure 1 corresponding to the Fourier signal at 0.000855 Hz=18.8 min. The repeating 18.8 min periods of the decomposition fit mirror the recurring pattern of maxima and minima over the primary data (black) over the entire 17000 sec analyzed.

Figure 4: Decomposition fit of data of Figure 1 corresponding to the Fourier signal at 288 sec=4.8 min revealed within each 18.8 min period for unevenly spaced maxima, two of which, labeled  and , were separated by 6 min and two of which labeled  and  were separated from each other and from maxima  and  by about 4 min [6 min+3 (4 min)=18 min]. From Morré DJ and DM Morré (2015) Synchronous Oscillations Intrinsic to Water: Applications to cellular time keeping and water treatment. Water 7: 2082-2100.

Segmental analyses (e.g., 1 to 6257 sec, 1794-11479 sec, 6257- 11479 sec, 6257-17728 sec, 13174-13728 sec, etc.) revealed the 286 sec period most clearly. However, when averaged over multiple segments, the overall amplitudes were slightly reduced and the characteristic 4 maxima periodic structure became less distinct. This appears to have been the result of occasional small shifts in the phase angle of the sine wave function. The period did not change but small shifts occurred horizontally along the time axis. The ortho-para oscillations are phased by low frequency electromagnetic fields [17] some of which might have occurred during the collection of the primary data to account for the small phase shifts observed.

Gudkov et al. [7] first reported laser-induced auto oscillations in the luminescence intensity with the blue-green region of pure water when measured at intervals of 1 sec over several hours without indications of damping. Wavelet transform analysis of the luminescence records revealed two characteristic periods of pulsations of about 300 and 1150 sec. These times correspond to the oscillation periods of the concentration ratios of the ortho and para spin isomers of water molecules measured previously by FTIR [5]. A similar phenomenon occurs in pure water in the absence of excitation by laser radiation [7,18] although at an intensity ca. 25% of that following laser excitation [7].

Consistently, Chernikov observed oscillations of the light scattering in water and aqueous protein solutions with periods on the same order of 1 to 6 and 15 to 20 min [6]. The method of complex wavelet transforms may be the most adequate method for problems of this kind [11]. Periods of nearly 18 and 5 min also have been observed previously by the wavelet transform analysis method [1].

The previously reported 18 min period for water is not an exact value but a trend in period length approximated between 18 and 20 min [5,14,19]. The findings of the present study provide a much more precise value of 18.8 min. Evidence that water vapor is a mixture of two independent states of liquid water with long lifetimes and two hydrogen bond types differing in energy led Pershin [9] to consider the two water states as independent fractions represented by ortho and para water respectively. Specifically “the energy of the hydrogen bond between ortho isomers of molecules which always rotate seems to be lower than between para molecules, a part of which cannot rotate at room temperature.”

Pershin concluded that this overheating-overcooling process may be a fundamental property of water, which manifests itself at any temperature and is not the result of perturbation of overcooled water by an optical pulse. Pershin’s findings [9] show “that such an evolution of the band center is steadily observed in water and at room temperature. Moreover, this overheating-overcooling process is approximated by a harmonic function also without noticeable damping.”

The findings are consistent with the interpretations of Pershin [9] and Drozdov and Nagorskaya [1] that the oscillations are the result of an alternation of two energetic water states with luminescence augmented autocatalytically by the laser-induced steady state formation of singlet oxygen [20]. Because of the similarity of the period lengths determined by Wavelet transformation methods, we propose that the oscillations in the luminescence data may result from energy discharged in the synchronized paired hydrogens of the water transition from their highest energy to their lowest energy states. Two such different energetic states are provided by alternation of the ratios of ortho and para nuclear spin isomers of water between two distinct energy states with the water luminescence representing the return of energy in the form of light as the highly synchronized ortho-para disequilibration returns from the high energy to the low energy state.

The differences in energies of the different spin isomers of water are small (less than 10^-24 erg) [10] and are much lower than the energy of thermal motion. Therefore, a spin-only interaction would not be expected to affect intermolecular interactions [10]. On the other hand, the absorption rates of ortho and para water from water vapor to various organic and inorganic sorbents have been observed to differ markedly with the binding of the para isomer. Estimates of the energy barriers that determine rates of absorption by these authors suggested that the difference in free energy barriers may exceed the energy of spin-spin and spin-orbit interaction by many orders and raises the possibility that the spin state of water may substantially influence physical, chemical and biological phenomena [21].

Moreover, recent studies, reviewed by Doherty and Kay [22] no longer fully support the prevailing models where generation of circadian rhythms is controlled primarily by transcriptional mechanisms.

Our findings do not directly answer the question of what is the fundamental period length of the ortho/para oscillations of water that appear to generate the ultradian rhythm suggested to underlie the biological clock. The actual period of the individual oscillations may be in the order of about 6 sec which, by a process of algebraic summation, would generate higher order oscillations the sum of which are no longer sinusoidal and give rise to “super” periods to generate a “composite wave” with an observed period length of 286 (12 sec × 24=288 sec) sec and ultimately the 1130 sec (18.8 min) period correlated with biological activity [2].

Based on analyses of luminescence data collected at intervals of 1 sec, a synchronized pattern of sinusoidal oscillations in laser-enhanced light emission from water with an 18.8 min period was observed recapitulating that previously attributed to synchronized alternation of water states represented by enrichment in either ortho or para spin pairs. The oscillations in light emission are interpreted as the result of synchronous energy discharge from the transition between the two energy states represented by ortho and para water enrichment.

We thank Lora Crist for assistance with numerical averaging and Peggy Runck for preparation of the manuscript.