Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
+44 1300 500008
ISSN: 2157-7544
+44 1300 500008
Research Article - (2012) Volume 3, Issue 1
The kinetics of oxidation of amitriptyline by potassium permanganate in aqueous sulphuric acid medium at 298K and at a constant ionic strength of 0.20 mol dm-3 has been investigated spectrophotometrically. The reaction exhibits 5:4 stoichiometry (5 Amitriptyline:4 KMnO4). The reaction was first order with respect to manganese(VII) concentration. The order with respect to amitriptyline was found to be less than unity (0.80). Increase in acid concentration increased the rate. The order with respect to acid concentration was also less than unity (0.40). The effect of added products, ionic strength and dielectric constant have been studied on the rate of reaction. The oxidation products were identified by using 2,4 DNP derivative, IR, GCMS spectral studies. A suitable mechanism was proposed on the basis of experimental results. The reaction constants involved in the different steps of the reaction mechanism were calculated. The activation parameters with respect to slow step of the mechanism was determined and discussed.
Scalable simulation, design, and optimization of the CO2 capture processes start with modeling of the thermodynamic properties, specifically vapor-liquid equilibrium (VLE) and chemical reaction equilibrium, as well as calorimetric properties. Accurate modeling of thermodynamic properties requires availability of reliable experimental data and a good model and accurate model to simulate VLE data. A thermodynamic property model capable of accurate representation of the vapor-liquid equilibrium (VLE) of the aqueous MEA-CO2 system is essential for a successful computer simulation of the process. In the last few decades, considerable progress has been made in modeling VLE of the acid gas (CO2 and H2S) in aqueous alkanolamine systems, including the aqueous MEA-CO2 system.
Many models have been applied to predict the adsorption of CO2 by MEA, some of them have been successful and others can be applied in a specific range of parameters such as temperature and concentration. The extended UNIQUAC model sticks out to be one of the best and they have been fewer applications in this respect despite its simplicity and the small number of its parameters. In this paper, we will be using this model using a different approach of regressing its parameters, and not based on the traditional regression methods but on multiple objective function using differential evolution algorithm.
Thermodynamic framework
Vapor liquid equilibrium: The processes discussed involve both chemical equilibria and multi-component phase equilibria. The liquid phase comprises both molecular species and ionic species, which makes the modelling non-trivial. The chemical reactions taking place in the liquid phase for MDEA-CO2-H2O can be expressed as:
Water ionization
2H2O↔ H3O++ OH− (1)
Dissociation of carbon dioxide
CO2 + 2H2O↔ H3O+ + HCO3− (2)
Dissociation of bicarbonate
HCO3− + H2O↔ H3O+ + CO32− (3)
Dissociation of protonated amine
MEAH+ + H2O↔ H3O++ + MEA (4)
MEACOO− (carbamate) reversion to bicarbamate
C3H6NO3− (MEACOO− ) + H2O↔C2H7NO(MEA) + HCO3− (5)
The model
Extended UNIQUAC: The extended UNIQUAC model expresses the excess Gibbs energy as the combination of three terms contributing to the total excess Gibbs energy: the entropic and enthalpy terms of the original UNIQUAC equation to consider the non-electrostatic interactions and, the electrostatic term (Debye Hückel):
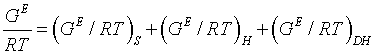 (6)
(6)
The first term i.e. the entropic term, is to describe the deviation from ideality due to the shapes and sizes of individual species in the solution and it is determined by the composition. This term is given as
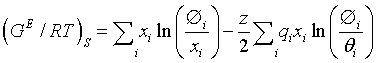 (7)
(7)
Where z is the coordination number arbitrarily set to 10. Volume fraction Øi and area fraction θi are
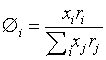
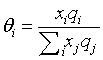
xi is the mole fraction of component i. The volume parameter ri and the surface area parameter qi are treated as adjustable parameters in this work.
The residual or the enthalpy term, is the other short range term of the UNIQUAC equation which is meant to take into account the energetic interactions between like and unlike species,
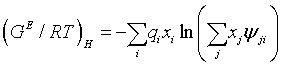 (8)
(8)
Where ψji is
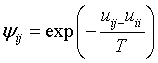
The adjustable interaction parameters (uji) of the UNIQUAC enthalpy term are assumed to be temperature dependent and are fitted to the following function of temperature
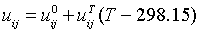 (9)
(9)
The Debye-Hückel expression used is the simplification of the original term given by Debye and Hückel for the electrostatic contribution to the excess Gibbs energy:
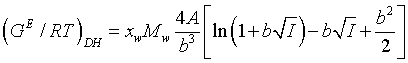 (10)
(10)
xwand Mw are the mole fraction and molar mass of water respectively. The parameter b is considered to be a constant equal to 1.50 (kg/mol)1/2. A is the Debye-Hückel constant given by
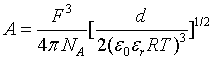
Where F (Cmol-1) is the Faraday’s constant, NA (mol-1) is Avogadro’s number, ε0 (C2 J-1m-1) is the vacuum permittivity, R (Jmol-1 K-1) the gas constant and T (K) is the temperature. d (kgm-3) and εr are the density and the relative permittivity of the solution respectively.
The Debye-Hückel parameter is considered temperature dependent which for the temperature range of 273.15 to 383.15 K can be written as
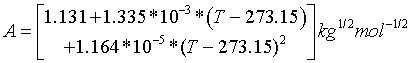
I (mol/kg H2O) is the ionic strength expressed as:
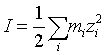 (11)
(11)
Where mi (mol/kgH2O) and zi are the molality and the charge number of ionic species i respectively.
There are no adjustable parameters in the Debye-Hückel term and the Debye-Hückel parameter is based on the density and dielectric constant of pure water. This means that the effect of MEA and other solute species on the dielectric constant of the solution is not considered and also by considering water as the single solvent, the density of pure water rather than that of the solution can be used. This strategy simplifies the calculations while the reasonable precision of the model is sustained. The vapor phase fugacities are calculated using the Soave-Redlich-Kwong (SRK) equation of state, no parameters to be adjusted for the SRK-EOS (Equation of State). Now that all the terms contributing to the total excess Gibbs energy are defined, the activity coefficients of the molecular and ionic species are obtained by partial molar differentiation of the Gibbs energy expressions
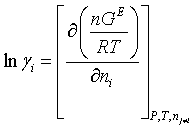 (12)
(12)
The symmetrical activity coefficient for water and the asymmetrical activity coefficients for the ions can be calculated as:
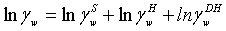 (13)
(13)
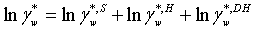 (14)
(14)
The Gibbs-Helmholtz equation is used for calculation of the symmetrical excess enthalpy of MEA-water solutions. The equation defines the temperature dependence of the excess Gibbs energy and therefore also of the activity coefficients:
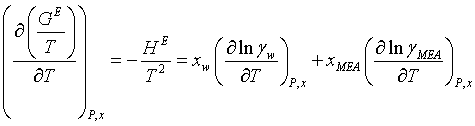 (15)
(15)
The experimental values and those calculated by the model are indicated by “exp” and “calc” respectively. P (bar) is the bubble point pressure, HE (Jmol-1) the excess enthalpy and ΔG° (J mol-1) is the change in the chemical potential by transferring one mole from liquid to solid phase and R (mol/kg H2O) is the gas constant.
Differential evolution
Storn and Price proposed Differential Evolution (DE) as a family of algorithms to solve real-parameter optimization problems [1]. The variants of DE are differentiated from each other by varying the mutation and/or the recombination operation within a common framework. However, in this study we used the DE/rand/1/exp variant of DE. Therefore, we describe DE with this variant.
DE works with a population of individuals xi G, i = 1, 2, . . . , p each representing a solution to the problem. DE individuals are encoded as real vectors of size which is the dimension of the problem. The number of individuals in a population is called population size and is denoted by P and the generation number is denoted by G. The initial population, P1 is created by randomly creating the vectors in appropriate search ranges. Then the fitness score of each individual is calculated through evaluation.
DE practices random parent selection regardless of their fitness values. In every generation, each individual xi G gets a chance to become the principal parent and to breed its own offspring mating with other randomly chosen auxiliary parents. Formally, for every principal parent xi G, i= 1, 2, . . . , p, three other auxiliary parents xGr1 , xGr2, xGr3 are selected randomly such that r1, r2, r3 ∈ {1, 2, . . . , p} and i ≠ r1 ≠ r2 ≠ r3. Then these three auxiliary parents participate in differential mutation operation to create a mutated individual xGmust as follows:
Where F is the amplification factor, a real-valued control parameter chosen from [0.1, 1.0] [2]. Subsequently, the mutated vector, xGmust, participates in exponential crossover operation with the principal parent xGito generate the trial individual or offspring xGchild. Exponential crossover is actually a cyclic two-point crossover in which CR, another control parameter of DE, determines how many consecutive genes of the mutated vector, xGmust, on average are copied to the offspring xGchild.
The selection scheme used in DE is also known as knockout competition. As the name suggests, DE plays a one-to-one competition between the principal parent, xiG, and its offspring xGchild to select the survivor for the next generation. The DE selection scheme can be described as follows:
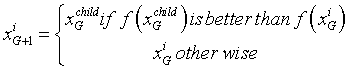 (16)
(16)
Repeating the above mentioned mutation and crossover operations on each individual of the current generation, DE creates a new generation of population which replaces the current generation. And this generation alternation process is iterated until the termination criteria is satisfied. The control parameters of DE (F, and P) are chosen beforehand and are kept constant throughout the search in this canonical version of the algorithm. The pseudo-code description of canonical DE is presented.
DE Algorithm
| DE Algorithm |
|
The estimation of the parameters of extended UNIQUAC was performed by minimizing the following objective function :
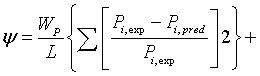
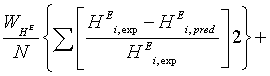
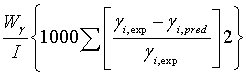 (17)
(17)
Where I, L, and N are the total number of experimentally determined, activity coefficient, VLE and excess enthalpy. In this investigation the data weighting factor, Wj=1, was used in all the parameter estimations. If, say for example, no VLE data was used in the parameter optimisation, the data weighting factor Wp was set to zero. The minimum objective function was minimized using differential evolution and Levenberg-Marquardt algorithms, where both results were compared.
During the parameters estimation, the quality of the fit was determined by the average absolute difference of the fit. The average absolute percentage difference were calculated from
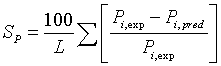 (18)
(18)
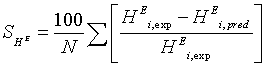 (19)
(19)
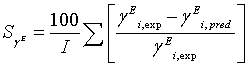 (20)
(20)
Before the ability of the UNIQUAC model was tested to simultaneously correlate all the available aqueous MEA aqueous mixture data, the three individual types of data: activity coefficient, total pressure, and excess enthalpy were regressed individually to ascertain the scatter in the data. In all cases, any data sets that significantly deviated from the regression results were rejected. In this work a rather liberal tolerance of 20% deviation from the regression value was used to reject out-lying data points.
A complete list of the data sets used in this investigation is presented in the following tables (Tables 1 to 6).
| VLE | ||
| MEA (Mole %) | Temperature (7°C) | Reference |
| 0-100 25, 50, 75 0-100 0-100 0-100 |
88-170 37-137 60, 67, 91.7 90 25, 35 |
1 2 3 4 5 |
| Excess Enthalpy | ||
| 0.59-98 0.15-0.97 15-67 |
25 25 25, 69 |
5 6 7 |
Table 1: MEA-H2O system data.
| MEA-H2O | ||
| Temperature (°C) 30-80 | MEA (wt%) 20 | Reference 8 |
Table 2: Densities data for MEA-H2O system.
| MEA- CO2-H2O | |||
| Temperature (°C) 40, 60, 80, 120, 134, 140 24, 40, 60, 80, 100, 120 80, 100 25, 60, 80 40, 80 40 30, 40, 50, 60, 70 |
MEA (wt%) 15.2 5, 15.3, 23.2, 31 15.3 15.3 15.3 15.3, 30 12.2 |
Loading 011-0.99 0.06-2.15 0.03-0.28 0.41-1.32 0.26-0.69 0.22-1.04 0.4600.91 |
Reference 9 10 11 12 13 14 15 |
Table 3: Ternary data for MEA-CO2-H2O system.
| Sources | Year | Components | Data Type |
| Leibush and Shorina [18] Conners [19] Lychkin et al.[20] Danilov et al. [21] Wohland [22] de Oliveira et al. [23] Touhara et al. [24] Nath and Bender [25] Buslaeva et al. [26] Lenard et al. [27] Kim et al. [28] Kling and Maurer [29] Chang et al. [30] Dohnal et al. [31] Posey [32] Cai et al. [33] Maham et al. [34] Park and Lee [35] Tochigi et al. [36] Tanaka et al. [37] |
1947 1958 1973 1974 1976 1980 1982 1983 1983 1987 1987 1991 1993 1994 1996 1996 1997 1997 1999 2001 |
MEA, DEA MEA MEA MEA, DEA MEA MEA, DEA MEA MEA MEA MEA MEA,DEA,MDEA MEA MEA,DEA,MDEA MEA MEA,DEA,MDEA MEA, DEA MEA, MDEA MEA MEA MEA |
VLE VLE γ γ VLE GE VLE, HE VLE HE VLE HE VLE γ HE HE VLE HE VLE VLE VLE |
Table 4: Other sources of data used.
| Species | r | q |
| MEA MEAH+ MEA carbamate |
4.12 7.95 4.14 |
4.67 7.11 3.23 |
Table 5: UNIQUAC volume parameters ® and surface area parameters (q).
| Pair | u0 | uT |
| MEA-H2O MEA-CO2 MEA-MEA MEA-HCO3- MEA-MEAH+ MEAH+- H2O MEAH+-CO2 MEAH+-HCO3- MEA carbamate-H2O |
157.60 -456.34 602.45 198.65 167.13 -60.11 -80.59 356.32 1400.00(set) |
1.39 12.56 0.42 0.06 -1.21 3.17 6.41 3.37 0.00(set) |
Table 6: UNIQUAC binary interaction parameters uij0 and uijT .
The volume and surface area parameters, r and q respectively, for MEA, MEAH+ and MEA carbamate are determined by fitting to experimental data. The binary interaction parameters that are chosen to be adjusted are regressed to all types of experimental data in order to get a well-rounded model as well as to ensure accurate representation of different properties.
Figure 1 shows the effect of CO2 concentration on the total pressure of the mixture. The model fits well with the experimental and especially for both cases studied, two extreme, 25oC and 120oC, temperatures and concentrations of carbon dioxide.
Figure 1: Model predictions and the experimental data (Lee et al. [38]) of the total pressure for CO2-MEA-H2O system at different MEA concentrations and temperatures.
Figure 2 presents a comparison fit between the DE algorithm and LM. The discrepancy between the two is quite noticeable at higher concentration of MEA. It is obvious when comparing the ADD% (γwater) in the cases of DE and LM. ADD% (γwater) for DE and LM are equal to 0.19 and 0.32, respectively.
Figure 3 shows a good representation of the model by predicting the total pressure of the binary system (MEA+H2O) at three different temperatures.
Figure 3: Prediction of the total pressure of the mixture (MEA+H2O) at different temperatures. Nath & Bender [3] data (T=60, 78 and 91.7°C).
Presented in Figure 4, are the excess Gibbs energy and excess entropy calculated by the model (line) and LM approach (dots). The plots give noticeable discrepancies between the two approaches.
The extended UQIQUAC model has been successfully applied with Differential Evolution algorithm to calculate the interaction parameters and to correlate the experimental data on thermodynamic properties of MEA-H2O-CO2 system. The model has validated a lot of experimental data, but more research should be carried out to compare DE with other genetic algorithms in Multiple Objective Optimization. The model can be used to support process modeling and simulation of the CO2 capture process with MEA.