Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Paper - (2019)Volume 8, Issue 2
Pressure and thermal energy of a novel hydrogen chemistry driven plasma is converted into kinetic energy using a converging-diverging nozzle, and the kinetic energy is converted to electricity in a novel highly efficient MHD cycle exploiting (i) the ability of silver to form nanoparticles at its melting point when exposed to oxygen and (ii) the ability of silver at its melting point to absorb up to 25 mole percent oxygen wherein the corresponding rates to support the cycle where experimentally confirmed. Equations for a constant pressure expansion of a constant conductivity working fluid in an MHD channel with uniform magnetic field demonstrated that as the flow decelerates the kinetic energy of the fluid is converted to MHD power in proportion to the loading factor W at a power density of 23.1 MW/liter, and the remaining fraction (1–W) of the kinetic energy is converted to fluid enthalpy that can be recovered wherein the MHD converter has no moving parts. Since the MHD efficiency may approach W=1, the electrical conversion of the power of the plasma into electricity may approach the efficiency of pressure-thermal to kinetic energy conversion wherein the corresponding nozzle efficiencies of 99% have been realized. This novel thermodynamic cycle enables closed liquid magnetohydrodynamic power conversion of a breakthrough clean hydrogen plasma power source into electrical power at a power density that is orders of magnitude higher than previously possible at an efficiency approaching unity.
Magnetohydrodynamic cycle; Silver nanoparticles; Silver-oxygen
Large, 100-1000 MW-scale, central generation power stations based on the Rankine and Brayton cycles have been the mainstays for electrical power generation for over 100 years with the latter becoming more dominant as inexpensive natural gas replaces coal. Each of these cycles are feasible due to the consumption of a natural resource, namely in essence an infinite supply of cold liquid water and cold atmospheric pressure air, respectively. In the case that each natural resource had to be returned to its original state, the efficiency of Ranking and Brayton cycles would be very low to negative. Magnetohydrodynamic (MHD) cycles that were explored extensively in the 60’s and 70’s mostly in the United States, Russia, and Japan were developed as potential replacement cycles [1-15]. An initial scheme was a liquid metal MHD cycle (LMMHD) that exploited the extraction of the kinetic energy of a liquid metal that was accelerated by a hot expanding gas that was heated in an external loop to which the gas was recycled following pushing the metal. Low efficiency of a few percent due to accelerator gas slippage with the liquid metal could not be surmounted [11-15].
Cycles that advanced to megawatt scale prototypes and even 100 MW scale commercial pilot plants were alkali metal seeded noble gas cycles and alkali salt seeded combustion gas cycles that were based on extracting thermal energy and pressure-volume (P-V) work. The seeded working gas was first accelerated in a convergingdiverging nozzle to Mach speed and then some fraction of the remaining P-V energy was extracted by further expanding of the resulting conductive jet in a MHD channel. The former included alkali metal seeded noble gas such as cesium metal seeded argon or helium gas heated by a thermal power source such as a combustion or nuclear power source. The latter included alkali metal seeded combustion gases such as potassium carbonate seeded coal combustion exhaust. In these cases, a number of challenges were encountered. The conductivity of seeded gas is very low such as 10 S/m, and the seeding typically requires temperatures of over 2000°C which was especially problematic for the cycles involving an external heat source due to the source operational temperature limitations and the feasibility of suitable heat exchangers that could operate at over 2000°C and transfer sufficient power given the high gas flow rates and corresponding limited heating time. Moreover, the electrodes that collect the MHD power were prone to destruction by the chemical corrosion of the seed gases as well as the arc formed between the ionized flow and a non-ionized, nonconductive layer formed near the electrodes. The latter nonconductive near-electrode zone formed due to unavailability of electrodes that could operate at a temperature of about the 2000°C limiting ionization temperature. Ultimately, these cycles were considered only as topping cycles for other power cycles such as at least one of Brayton and Rankine cycles due to the loss of most of the power at the exhaust temperature of 2000°C [1-3].
A novel power source that produces powerful plasma presents an
opportunity to reconsider MHD power conversion. The power is
developed by reacting atomic hydrogen with HOH catalyst to form
fractional Rydberg energy states H (1/p) called "hydrino atoms"
where in 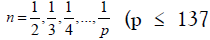 is an integer) replaces the well-known
parameter n=integer in the Rydberg equation for hydrogen excited
states. The transition of H to a stable hydrino state
is an integer) replaces the well-known
parameter n=integer in the Rydberg equation for hydrogen excited
states. The transition of H to a stable hydrino state 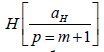 having a binding energy of p2 ⋅13.6 eV occurs by a non-radiative
resonance energy transfer of m.27.2 eV (m is an integer) to a
matched energy acceptor [16]. The nascent H2O molecule (not
hydrogen bonded in solid, liquid, or gaseous state) serves as the
catalyst by accepting 81.6 eV (m=3) to form an intermediate
that decays with the emission of a continuum band with a short
wavelength cut-off of 10.1 nm and energy of 122.4 eV [16-23]. It was
reported previously that hydrated silver shots comprising a source
of H and HOH catalyst were ignited by passing a low voltage, high
current through the shot to produce explosive plasma that emitted
brilliant light predominantly in the short-wavelength 10 to 300
nm region [17]. Based on Stark broadening, the initially optically
thick essentially 100% ionized plasma expanded at sound speed or
greater and thinned to emit EUV and UV light. The peak power
of 20 MW was measured using absolute spectroscopy over the
22.8-647 nm regions wherein the optical emission energy was 250
times the applied energy. Continuous megawatt-level power was
recorded on a hydrino reactor wherein continuous brilliant plasma
was maintained by HOH and H produced from water-entrained
injected molten silver matrix. The molten fuel produced the same
EUV spectrum as the shots, but EUV light converted to 5700 K
blackbody radiation of about 1 m2 surface area with a positive
feedback cycle of silver vaporization and absorption of the hydrino
reaction emission with the plasma becoming increasingly optically
thick. The catalysis reaction product H2(1/4) was identified by
Raman spectroscopy, photoluminescence emission spectroscopy,
X-ray photoelectron spectroscopy, and MAS 1H NMR.
having a binding energy of p2 ⋅13.6 eV occurs by a non-radiative
resonance energy transfer of m.27.2 eV (m is an integer) to a
matched energy acceptor [16]. The nascent H2O molecule (not
hydrogen bonded in solid, liquid, or gaseous state) serves as the
catalyst by accepting 81.6 eV (m=3) to form an intermediate
that decays with the emission of a continuum band with a short
wavelength cut-off of 10.1 nm and energy of 122.4 eV [16-23]. It was
reported previously that hydrated silver shots comprising a source
of H and HOH catalyst were ignited by passing a low voltage, high
current through the shot to produce explosive plasma that emitted
brilliant light predominantly in the short-wavelength 10 to 300
nm region [17]. Based on Stark broadening, the initially optically
thick essentially 100% ionized plasma expanded at sound speed or
greater and thinned to emit EUV and UV light. The peak power
of 20 MW was measured using absolute spectroscopy over the
22.8-647 nm regions wherein the optical emission energy was 250
times the applied energy. Continuous megawatt-level power was
recorded on a hydrino reactor wherein continuous brilliant plasma
was maintained by HOH and H produced from water-entrained
injected molten silver matrix. The molten fuel produced the same
EUV spectrum as the shots, but EUV light converted to 5700 K
blackbody radiation of about 1 m2 surface area with a positive
feedback cycle of silver vaporization and absorption of the hydrino
reaction emission with the plasma becoming increasingly optically
thick. The catalysis reaction product H2(1/4) was identified by
Raman spectroscopy, photoluminescence emission spectroscopy,
X-ray photoelectron spectroscopy, and MAS 1H NMR.
The quartz SunCell® power system shown in Figure 1 was engineered to maintain the hydrino reaction. The SunCell® power system comprises (i) a reaction cell chamber; (ii) reactants comprising nascent H2O catalyst, a source of atomic hydrogen, and a molten silver metal; (iii) a molten metal injection system comprising two molten silver reservoirs each comprising an injection tube and an induction electromagnetic pump comprising a source of alternating magnetic field through a shorted loop of molten silver that induces an alternating current in the metal and a source of in-phase alternating vector-crossed magnetic field; (iv) an induction ignition system comprising a source of electrical power to supply high-current electrical energy sufficient to cause the reactants to react to form plasma; and (v) a magnetohydrodynamic (MHD) power converter. The induction ignition system comprises a source of alternating magnetic field through a shorted loop of molten silver that generates an alternating current in the metal that comprises the ignition current. The source of alternating magnetic field is a primary transformer winding comprising a transformer electromagnet and a transformer magnetic yoke, and the silver serves as a secondary transformer winding such as a single turn shorted winding that encloses the primary transformer winding and comprises as an induction current loop. The reservoirs further comprise a molten metal cross connecting channel that connects the two reservoirs such that the current loop encloses the transformer yoke wherein the induction current loop comprises the current generated in molten silver contained in the reservoirs, the cross connecting channel, the silver in the injector tubes, and the injected streams of molten silver that intersect to complete the induction current loop. The powerful plasma formed by the ignition system is converted to electricity by the MHD power converter. The MHD power converter comprises a converging-diverging nozzle connected to the reaction cell chamber, a magnetohydrodynamic channel, electrodes, magnets, a metal collection system, a metal recirculation system, a heat exchanger, and optionally a gas recirculation system.
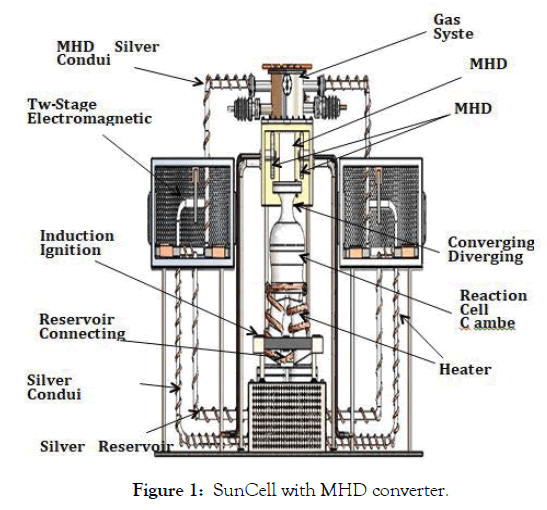
Figure 1: SunCell with MHD converter.
Mated to a suitable direct power extraction technology (DPET), the SunCell having the capability of generating over 100 kW/ litre presents an opportunity for compact pollution-free power generation that is independent of fuels or grid infrastructure. Magnetohydrodynamic conversion is a potential emerging DPET to directly convert the plasma and thermal power of the hydrino reaction into DC electricity. Inverters and power conditioning hardware are readily available to convert DC into AC to meet conventional load requirements. Some advantages are that (i) basic research development has been supported by energy agencies worldwide; (ii) MHD offers significant power generation efficiency for a cycle that recovers the kinetic energy of a highly conductive jet of plasma and liquid conductor; (iii) MHD comprises the simplest electrical power generation system physically possible; (iv) MHD has no moving mechanical parts; (v) MHD has the potential of being of extraordinarily compact size with DC power output that could be used directly for most modern lightning, resistive heating, electronics, and motor applications, and (vi) prototype MHD generators have demonstrated some large-scale commercial feasibility. These features present an opportunity for dramatic reductions in capital and maintenance cost. By exploiting features of the SunCell, a SunCell-MHD power generator presents additional unique advantages. For example, conventional MHD failure modes of very low conductivity and coking and corrosion of ion-seeded combustion gas are eliminated by SunCell-MHD. Silver working medium protects rather than corrodes the refractory metal electrodes. ANSYS Simulation Software conductivity modeling predicts a million-fold increase over that of ion-seeded combustion flame with a corresponding very significant increase in power density results due to the linear dependence of the MHD power on the conductivity. Moreover, based on experimental measurements, the prior loss of conductivity with temperature drop in the MHD channel and at the electrodes will not occur to a significant extent in the case of the SunCell plasma. Thus, high voltage electrical arcing from the jet to the electrodes is avoided, and much higher power efficiency is possible. In a novel thermodynamic cycle reported in this article, the majority of the SunCell reaction chamber plasma power may be converted to electricity by first conversion of the plasma power to kinetic energy (KE) in a conductive flow using a converging diverging nozzle and the KE of the flow is converted into electricity in the MHD channel. Additional efficiency may be realized through heat recovery due to molten silver recirculation rather than a working gas such as argon and the seed material of a closed conventional MHD cycle. Multistage turbo machinery with intercoolers and the inherent large power consumption with a corresponding negative impact on efficiency may be avoided.
We considered a number of MHD cycles for conversion of the powerful plasma formed by reacting atomic hydrogen with HOH catalyst to form hydrinos. Exploiting two extraordinary phenomena of silver-oxygen system, the ability of silver to form nanoparticles at its melting point when exposed to oxygen and the ability of silver at its melting point to absorb up to 25 mole percent oxygen, we developed a highly efficient and unique thermodynamic cycle for MHD conversion having features of a P-V cycle and a liquid MHD cycle.
The electrical power outputs of liquid metal magnetohydrodynamic (LMMHD) converters studied in the past converge to the corresponding kinetic energy change in the channel as given by representative Eq. (26) of Weinberg and Hayes [15]. However, a very small fraction of the thermal power of the corresponding source couples to propelling the working fluid liquid metal to give a net kinetic energy for a closed cycle. In this report, we analyse a LMMHD-type cycle whereby a powerful, highly-conductive jet flow forms comprising an oxygen and silver nanoparticle aerosol that is facilitated by two unique properties of silver and oxygen at silver’s melting point. In the presence of oxygen, molten silver forms nanoparticles at high rates that behave similarly to large molecules that approximately obey the ideal gas law. The aerosol forms at the melting point of silver (962°C); thus, a molecular gas having thermodynamic properties akin to silver atoms can form at a temperature well below the silver boiling point of 2162°C. This unique property of silver facilitates a thermodynamic cycle avoiding the input of the very high heat of vaporization of 254 kJ/ mole that is lost at the end MHD channel during condensation and recycling in a traditional gas expansion cycle. Moreover, molten silver at its melting point temperature can absorb an enormous amount of oxygen gas that may dissolve in the melt at the end of MHD channel and be electromagnetically (EM) pumped with the molten silver to be recirculated to the reaction cell chamber. The high temperature in the reaction cell chamber causes the oxygen to be released to serve as the accelerator gas of the resulting oxygen and silver aerosol. The thermal power released by the hydrino reaction in the reaction cell chamber causes a high pressure to rise, and a high-power silver plasma jet exits the MHD nozzle and enters the MHD channel wherein MHD kinetic to electric power conversion occurs. Due to the small particle size there should be no gas slippage as the oxygen gas accelerates the aerosol of silver nanoparticles particles as evidenced in Weinberg [14]. Thermal equilibrium of the mixture should be maintained as the mixture propagates through a mixing chamber and the nozzle due to the rapid electron heating by the plasma which will have a single blackbody temperature. The efficiency can be very high since (i) conversion of thermal energy into kinetic energy by expansion of a hot gas in a diverging converging nozzle can approach an efficiency of 100%, (ii) the channel efficiency approaches the loading factor as shown by Eqs. (17) and (18), (iii) the residual kinetic energy that is dissipated in the channel heats the silver-oxygen aerosol that is conserved as an addition to the thermal energy inventory of the aerosol, (iv) the silver is condensed or coalesced at the end of the MHD channel, the oxygen is absorbed by the liquid silver, and both are returned to the reaction cell chamber with the conserved channel thermal inventory, and (v) the accelerator gas is returned by very low power electromagnetic pumping (Eq. (52)) of the molten metal carrying the gas in solution rather than by very energy intensive multistage intercooled gas compression of the gas. A radiative or water-cooled heat exchanger may be added to the end wall of the MHD channel if theoretical conversion efficiencies are not achieved.
The solubility of atmospheric pressure oxygen in silver increases as the temperature approaches the melting point wherein the solubility is up to about 40 to 50 volumes of oxygen for volume of silver. Moreover, the solubility of oxygen in silver increases with oxygen atmospheric pressure in equilibrium with the dissolved oxygen. A high mole fraction of oxygen in silver may be achieved at high O2 pressure as shown by Assal et al. [24]. For example, there is a eutectic between Ag and Ag2O at a temperature of 804 K, an oxygen partial pressure of 526 bar (5.26 × 107 Pa), and an oxygen mole fraction in the liquid phase of 0.25.
The incorporation of oxygen atoms into silver is dramatically increased beyond that which may be achieved by gaseous solvation at a given oxygen pressure and silver temperature by converting the molecular oxygen to atomic oxygen [25]. The relationship of oxygen solubility in liquid silver is about proportional to the gaseous oxygen pressure to the ½ power since oxygen absorbs into silver as atomic. When O atoms instead of O2 molecules are involved in the oxidation reaction with silver, AgO as well as Ag2O are thermodynamically stable even at very low O2 pressures, AgO is more stable than Ag2O, and it is thermo-dynamically possible to oxidize Ag2O to AgO, which may be impossible with O2 molecules. To exploit the superior solubility of O atoms during the MHD cycle, the MHD channel plasma jet may be maintained by the hydrino reaction to maintain the formation of O atoms from O2 molecules. A composition such as the eutectic comprising 0.25 mole fraction oxygen incorporated in molten silver may be formed at the end of the MHD channel and pumped to the reaction cell chamber to recycle the silver and oxygen. The MHD cycle further comprises the release of the oxygen in the reaction cell chamber with a dramatic temperature and pressure increase due to the hydrino plasma reaction followed by isenthalpic expansion in the MHD nozzle section to form an aerosol jet and nearly isobaric flow of the jet in the MHD channel.
To successfully convert the thermal and pressure-volume energy inventory in the reaction cell chamber into kinetic energy in the MHD channel by isentropic expansion, the oxygen must effectively accelerate the silver in the converging-diverging nozzle. One of the main failure modes of LMMHD is slippage of the accelerator gas past large liquid metal particles. Ideally the metal particles behave as molecules, and the conversion of thermal energy into the kinetic energy of the plasma jet that flows into the MHD channel approximately obeys the ideal gas laws for isentropic expansion, the most efficient means possible. Consider the case wherein the reaction cell chamber atmosphere is oxygen, the injected molten metal is silver, and the oxygen promotes the formation of an aerosol of silver nanoparticles. The silver nanoparticles are in the free molecular regime when they are small compared to the mean free path of the suspending gas. Mathematically, the Knudsen number Kn given by
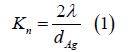
is such that Kn>>1 wherein λ is the mean path of the suspending oxygen gas and dAg is the diameter of the silver particle. After Levine [26], the mean path λAof a gas A of diameter dA colliding with a second gas B of diameter dB and mole fraction fB is given by
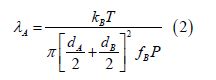
For the gas parameters of 6000 K temperature T, 5 atmospheres (5 × 105 N/m2) pressure P atomic oxygen, 12.5 mole% O2 corresponding to a gas fraction O2 f of 0.125, and 87.5 mole% silver corresponding to a silver gas fraction fAg of 0.875, the mean path λO2 of the suspending oxygen gas of molecular diameter dO2 of 1.2 × 10-10 m colliding with a silver particle of diameter dAg of 5 × 10-9 m given by Eq. (17) is
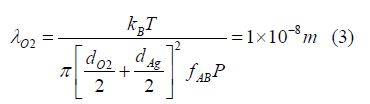
Where in kB is the Boltzmann constant. The molecular regime is about satisfied for silver aerosol particles having a 5 nm diameter corresponding to about 3800 silver atoms. In this regime, particles interact with the suspending gas through elastic collisions with the gas molecules. Thereby, the particles behave similarly to gas molecules wherein the gas molecules and particles are in continuous and random motion, there is no loss or gain of kinetic energy when any particles collide, and the average kinetic energy is the same for both particles and molecules and is a function of the common temperature.
In an exemplary MHD thermodynamic cycle: (i) silver nanoparticles form in the reaction cell chamber wherein the nanoparticles may be transported by at least one of thermophoresis and thermal gradients that select for ones in the molecular regime; (ii) the hydrino plasma reaction in the presence of the released O forms high temperature and pressure 25 mole% O, 12.5% O2 and 87.5 mole% silver nanoparticle gas that flows into the nozzle entrance; (iii) 12.5 mole% O2 and 87.5 mole% silver nanoparticle gas undergoes nozzle expansion, (iv) the resulting kinetic energy of the jet is converted to electricity in the MHD channel; (v) the nanoparticles increase in size in the MHD channel and coalesce to silver liquid at the end of the MHD channel, (vi) liquid silver absorbs 25 mole% O, and (vii) EM pumps pump the liquid mixture back to the reaction cell chamber.
Given the ability of silver to form suitable nanoparticles in the molecular regime and absorb a suitable mass of oxygen to recycle the accelerator gas, oxygen in this case, without use of turbo machinery, the feasibility of the oxygen and silver nanoparticle aerosol MHD cycle depends on the kinetics of the aerosol formation rate and the rate that oxygen can be absorbed into and degassed from molten silver. It has been well established in literature that oxygen is highly soluble in liquid silver. However, there is a lack of quantitative data regarding the kinetics of this phenomenon. The rate of oxygen absorption by silver with respect to the exposed surface area and volume was determined to design an MHD cycle using this unique property of silver. There appears to be no literature on the fuming behaviour of silver. The corresponding kinetic studies were performed as well.
The aerosolization rate of pure silver was measured by heating pellets placed in pure graphite crucibles using a tri-arc melt furnace (Model: Materials Research Furnaces TA-200). The arc furnace consists of 3 electrodes made from 2% Th-W that can be used to heat samples to temperatures in excess of 2400°C. As a control experiment, a pure Ag pellet with a known mass was heated under a constant Ar flow set to 5 L/min. The temperature of the pellet and crucible was measured at 1590°C using a 2-color optical pyrometer (Model: Omega iR2C). Under a pure Ar atmosphere, no aerosolization was observed and the change in mass of the Ag pellet after the experiment was negligible. When the gas composition was changed to a 1% O2–99% Ar mixture and the experiment was repeated, the pellet showed significant fuming and filled the reaction chamber with a fine white smoke. After accounting for the lost mass in the graphite crucible due to oxidation, the change in mass of the Ag pellet was carefully recorded. These experiments were repeated at increasingly higher temperatures until reaching a maximum of 2340°C. By measuring the exposed surface area of each pellet in contact with the gas mixture, the mass loss per time per unit area (aerosolization rate) was then calculated. Results show higher aerosolization rates with increasing temperatures up to 11.9 mg/s/cm2 recorded at 2340°C. The silver particles were collected on a silicon wafer and analyzed by TEM. About 20% of the particles were nanoparticles of about 5 nm diameter. The surface area of a 5 nm diameter nanoparticle is 7.8 × 10-13 cm2 and the number of nanoparticles corresponding to a mass flow rate of 0.5 kg/s is 7.3 × 1020 particles/s corresponding to an area velocity of 5.71 × 108 cm2/s. As the injected silver breaks into successively smaller particles, the area is predicted to be sufficient to achieve the desired nanoparticle flow rate.
Due to the reversibility of desorption and absorption and the ability to determine the amount of oxygen absorbed in silver based on the phase diagram, the silver oxygen desorption rate was determined as a function of surface area and volume at its melting point of 962°C following exposure to 760 Torr of pure O2 for 10 minutes. Based on the phase diagram the silver was loaded to 0.2 wt% before desorption [27,28].
Specifically, each silver sample was held in an alumina boat of a variable measured volume and surface area. The boat was placed at the center of a 26'' long quartz tube with an OD of 25 mm. The tube was fitted on one end with a gas supply line to facilitate evacuation and backfill with O2. The other end has fittings to insert a thermocouple into the tube and to attach a 1000 Torr Baratron to record temperature and pressure data, respectively. The quartz tube was then placed in a tube furnace to heat the sample. The sample was heated to just below the silver melting point (962°C) and then O2 was introduced into the tube. The flow was controlled by a mass flow controller, and the flow duration was recorded. Once the tube pressure was around 760 Torr, the sample was heated to just above 962°C to melt the silver. The tube pressure dropped as the oxygen was absorbed by the liquid silver. The sample was held at this temperature for 10 minutes to fully load the silver to its equilibrium at 760 Torr O2 at 962°C and then the sample was rapidly cooled to drop the temperature below the point of silver solidification. Since oxygen is highly insoluble in solid silver, all of the oxygen absorbed by the silver was then released and the resulting pressure spike as a function of time was recorded by the Baratron. Based on the time trace and the 0.2 wt% loading, the rate that silver desorbs was determined. This data also applies to the rate of absorption under the same conditions. The desorption rate showed a linear dependence on both the surface area and the volume of the silver. The calculated rate of oxygen desorption/absorption with respect to the surface area is 4 mg/s/ cm2. The area velocity of 5 nm diameter nanoparticles flowing at 0.5 kg/s is 5.71 × 108 cm2/s that is predicted to be sufficient to achieve the desired oxygen absorption rate.
The feasibility of the current LMMD-type cycle further depends on the high ionization of the plasma in the channel to maintain the conductivity used in Eq. (9) and to facilitate atomic oxygen absorption into molten silver at the end of the MHD channel. It was reported previously that a Voigt-fit to the spectral profile of the 656.28 nm H Balmer α line measured using the Jobin Yvon Horiba 1250M spectrometer showed a full width half maximum (FWHM) of 14 Å [17]. An electron density of 4 × 1023/m3 was determined from the extraordinary Stark broadening indicating that the high-pressure (5 atm) plasma was almost completely ionized. An exemplary, SunCell® plasma jet into atmosphere is shown in Figure 2.
For a gaseous mixture of oxygen and silver nanoparticles, the temperature of oxygen and silver nanoparticles in the free molecular regime is the same such that the ideal gas equations apply to estimate the acceleration of the gas mixture in nozzle expansion wherein the mixture of O2 and nanoparticles have a common kinetic energy at the common temperature. The acceleration of the gas mixture comprising molten metal nanoparticles such as silver nanoparticles in a converging-diverging nozzle may be treated as the isentropic expansion of ideal gas/vapor in the converging-diverging nozzle. Given stagnation temperature T0; stagnation pressure p0; gas constant Rv; and specific heat ratio k, the thermodynamic parameters may be calculated using the equations of Liepmann and Roshko [27]. The stagnation sonic velocity c0 and density ρ0 are given by
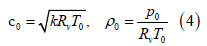
The nozzle throat conditions (Mach number Ma*=1) are given by:
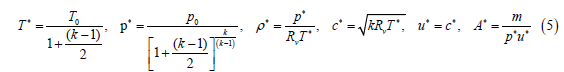
where u is the velocity, m is the mass flow, and A is the nozzle cross sectional area. The nozzle exit conditions (exit Mach number=Ma) are given by:
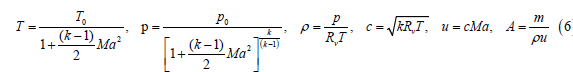
Based on the phase diagram of Assal et al. [24], the background partial pressure of O2 in the reaction cell chamber of the SunCell® (Figure 1) is maintained at >100 atm to achieve up to 25 mol% O absorption in silver at the exit of the MHD channel. Since gas acceleration is driven by pressure differentials, the pressures used in this analysis are differential pressures. Due to the high molecular weight of the nanoparticles, the MHD conversion parameters are similar to those of LMMHD wherein the MHD working medium is dense and travels at low velocity relative to gaseous expansion. Irrespective of the nature of an ideal gas, a reasonable limit to the efficiency of the conversion of thermal-pressure power inventory of the reaction cell chamber into kinetic energy power at the inlet to the MHD channel is determined by the efficiency of a converging diverging nozzle wherein the loses are frictional in nature. With the proper design, nozzle efficiencies can be very high. Nozzle efficiencies of 99% have been realized [29].

Figure 2:SunCell® plasma jet, ejected through a 2 cm diameter orifice in the wall of the SunCell®.
Lorentz force and power
A conducting fluid enters the MHD channel with velocity u0 at temperature T0 and pressure p0, as sketched in Figure 3. The channel cross section is square, with side length d=d(x), and the channel length is L. The flow is adiabatic and variations in the cross-channel direction are ignored: The flow is assumed onedimensional.
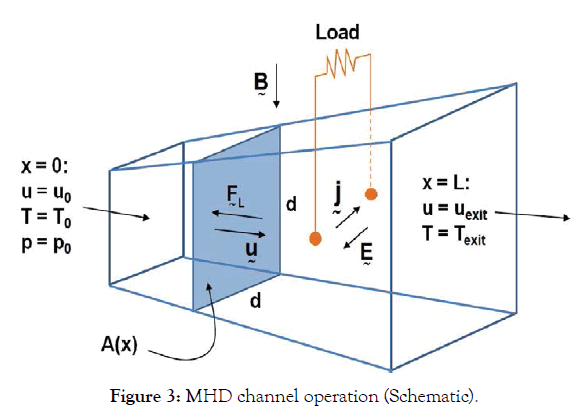
Figure 3:MHD channel operation (Schematic).
Because of the fluid conductivity, σ, a uniform magnetic field of magnitude B acting normal to the channel axis induces a crosschannel current in the fluid, which passes through a resistive load connecting the channel walls, which are parallel to the field. Because of the current passing through the load an electric field E is established counter to the current flow in the fluid. This results in the current density j=σ (u × B-E). The magnitude of the current density is
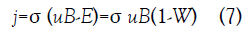
where W=E/(uB) is the constant loading factor which ranges from zero for a short circuit to unity for an open circuit. The fluid velocity u, electric field E, and current density j are all functions of axial position x in the channel. The orthogonal magnetic field and current result in a force which acts along the channel axis opposing the flow. The force per unit volume is the Lorentz force FL=j × B with magnitude
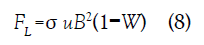
The rate at which energy is extracted from the fluid, per unit volume, is
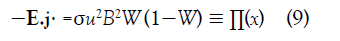
where Π(x) is the local MHD power per unit volume.
Conservation laws and constant pressure flow in the channel
In view of the Lorentz force and MHD power per unit volume, conservation of mass, momentum and energy in the fluid require
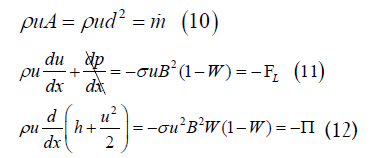
where ρ and h are the fluid density and enthalpy per unit mass
and 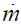 is the mass flow rate. It is assumed that the channel
cross section A(x) varies in such a way that the pressure gradient vanishes everywhere in the channel: dp/dx=0. Then from Eq.
(11) the velocity must decrease: du < 0. Further, the entropy per
unit mass s must increase in the flow direction because the flow is
adiabatic with current flow through the finite conductivity fluid.
Then Tds=dh=CpdT requires that temperature increases in the
flow direction: dT>0. And since the pressure is constant dρ<0 so
mass conversion
is the mass flow rate. It is assumed that the channel
cross section A(x) varies in such a way that the pressure gradient vanishes everywhere in the channel: dp/dx=0. Then from Eq.
(11) the velocity must decrease: du < 0. Further, the entropy per
unit mass s must increase in the flow direction because the flow is
adiabatic with current flow through the finite conductivity fluid.
Then Tds=dh=CpdT requires that temperature increases in the
flow direction: dT>0. And since the pressure is constant dρ<0 so
mass conversion
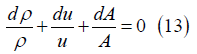
requires that temperature increases in the flow direction: dT>0.
Conversion of kinetic energy to MHD power for constant pressure flow
From Eqs. (10) and (11),
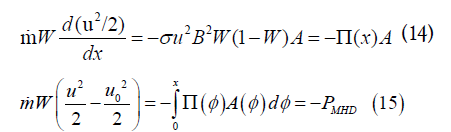
Where, PMHD is the MHD power output from the channel between the inlet and position x. PMHD is the fraction W times the rate of kinetic energy decrease from channel inlet to x:s
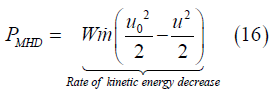
Integrating energy conservation Eq. (12) in the same way yields
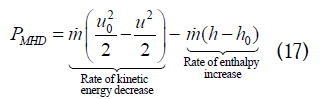
where h is the fluid enthalpy at x. Eq. (17) is a thermodynamic result that is valid for any pressure distribution in the channel, however, Eq. (16) holds only for constant pressure flow. From Eqs. (16) and (17), the rate of enthalpy increase from channel inlet to x is the fraction (1–W) times the rate of kinetic energy decrease:
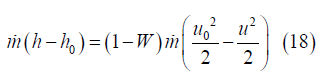
These results are valid independent of the nature of the working fluid.
Oxygen/Silver nanoparticle gas mixture
Consider a gas mixture of molecular oxygen and silver
nanoparticles at the mixture temperature T and pressure p.
The silver nanoparticles, here denoted by the symbol AgN, are
each comprised of N silver atoms. The mole fractions of oxygen
and nanoparticles in the mixture are 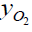 and yAgN=1–
and yAgN=1– 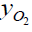 ,
respectively. The molecular weights of atomic silver and oxygen
are MAg=107.9 and MO2=32.00 g/mol, respectively, the molecular
weight of the nanoparticle gas is MAgN=NMAg and the molecular
weight of the O2/AgN gas mixture is
,
respectively. The molecular weights of atomic silver and oxygen
are MAg=107.9 and MO2=32.00 g/mol, respectively, the molecular
weight of the nanoparticle gas is MAgN=NMAg and the molecular
weight of the O2/AgN gas mixture is
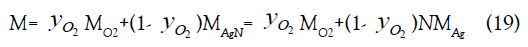
The mixture molecular weight depends linearly on both the oxygen
mole fraction and nanoparticle size N, increasing with N and
decreasing with 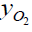 .
.
It is assumed that the oxygen, existing alone at the mixture
temperature T and pressure p 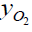 , and the nanoparticles, existing
alone at T and pressure pyAgN, each behave as ideal gases. The
silver nanoparticles are treated as rigid particles with no internal
structure and therefore the entire energy of a nanoparticle is due to
translation. The nanoparticle gas molar constant pressure specific
heat is
, and the nanoparticles, existing
alone at T and pressure pyAgN, each behave as ideal gases. The
silver nanoparticles are treated as rigid particles with no internal
structure and therefore the entire energy of a nanoparticle is due to
translation. The nanoparticle gas molar constant pressure specific
heat is
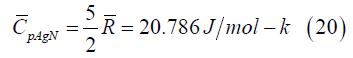
where, 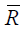 =8.31451 J/mol-K is the universal gas constant. This molar
specific heat is a pure constant, independent of the nanoparticle
size N. The oxygen molecules have translational, rotational and
vibrational energy. In view of the expansion temperature ranges
considered later, the oxygen molar constant pressure specific heat
is assumed constant at the value corresponding to 1500 K. The
molar constant pressure specific heat of oxygen is given by van
Wylen et al. [30] as
=8.31451 J/mol-K is the universal gas constant. This molar
specific heat is a pure constant, independent of the nanoparticle
size N. The oxygen molecules have translational, rotational and
vibrational energy. In view of the expansion temperature ranges
considered later, the oxygen molar constant pressure specific heat
is assumed constant at the value corresponding to 1500 K. The
molar constant pressure specific heat of oxygen is given by van
Wylen et al. [30] as
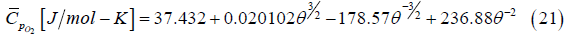
where
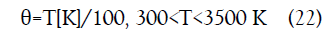
For T = 1500 K, Eqs. (21-22) yield 36.58 J/mol-K.
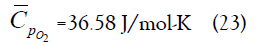
The constituent gases are perfect gases because they behave ideally and have constant specific heats, and therefore the mixture is also a perfect gas. Hence the oxygen molecules and nanoparticles in the mixture have the same average kinetic energy.
The gas constant, molar specific heat and mass-weighted specific heat for the O2/AgN gas mixture are
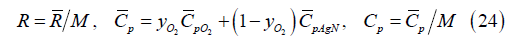
and the mixture specific heat ratio is
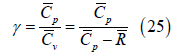
While the mixture molar specific heat and specific heat ratio depend only on the oxygen mole fraction, the mixture molecular weight, gas constant and mass-weighted specific heat depend on both the oxygen mole fraction and the size of the nanoparticles, N, as shown in Figure 4. Note the dramatic increase and decrease in mixture molecular weight and mass-weighted specific heat, respectively, for increasing nanoparticle size at constant oxygen mole fraction.
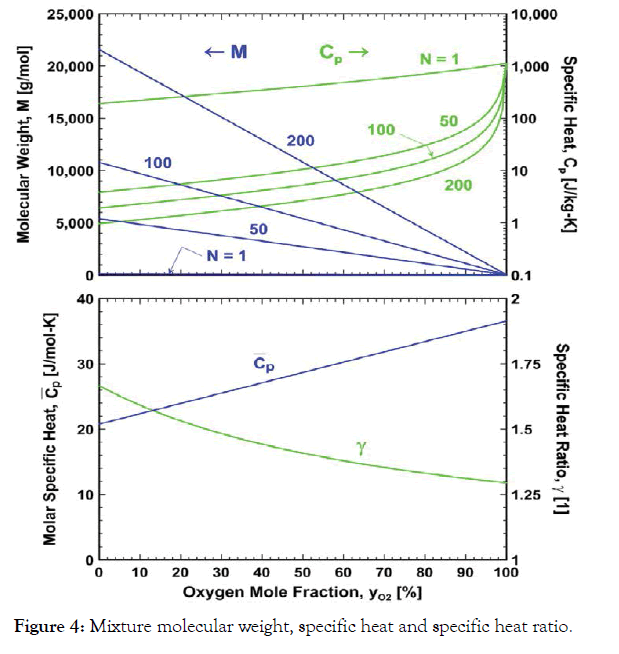
Figure 4:Mixture molecular weight, specific heat and specific heat ratio.
Mixture expansion in the channel
Temperature: From momentum and energy conservation
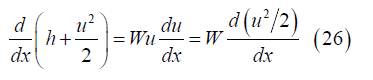
Then
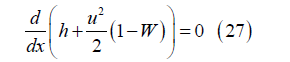
and integrating from the channel inlet to position x with dh=CpdT for the ideal gas mixture yields
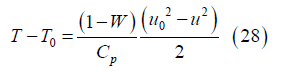
Rearranging, this becomes
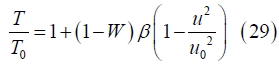
where
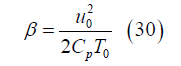
is a relative measure of the gas kinetic energy and enthalpy at the channel inlet. For a gas mixture with 50% oxygen mole fraction and nanoparticles encompassing 100 silver atoms entering the channel at 2000 K with 1000 m/s velocity, β ~ 47. This same mixture has β=1 if the inlet velocity is about 146 m/s.
Velocity: From momentum conservation, with density ρ=p0/(RT),
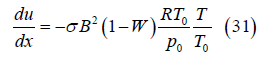
Substituting for temperature from Eq. (29), rearranging and integrating from the entrance to position x in the channel yields
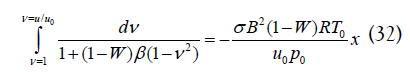
Simplifying the integral results in
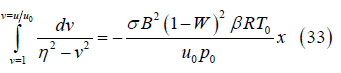
where
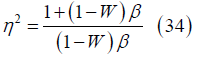
and then
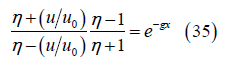
The constant g in the exponent, which has dimensions of reciprocal length, is
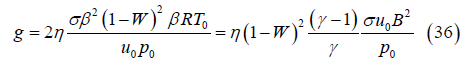
Solving for the velocity ratio results in
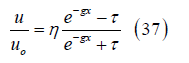
where
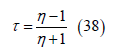
Although the velocity variation depends on the exponential decay terms e-gx, the velocity decay has little resemblance to an exponential decay. Rather, u(x) generally has downward concavity.
The gas decelerates everywhere in the channel and is arrested where
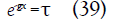
which corresponds to the axial position
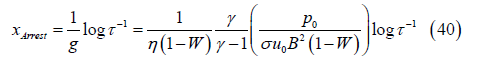
This distance is larger for smaller values of σu0B2(1-W), which is the Lorentz force at the channel inlet, and for larger pressure. Gases at higher pressure and therefore greater density can sustain forward motion against the adverse Lorentz force for a greater distance. Also, the distance xArrest will be seen to decrease with increasing inlet velocity u0, a counter-intuitive result that is explored later
Channel cross section: From momentum and mass conservation
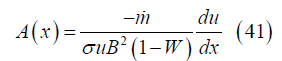
Substituting for the velocity and noting the velocity derivative
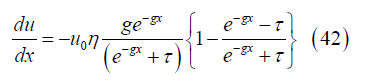
with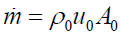 leads to the local cross section area
leads to the local cross section area
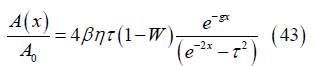
Channel volume: The channel volume V between the channel inlet and position x can be obtained from the cross section by integration
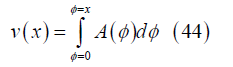
or, more easily, from momentum conservation:
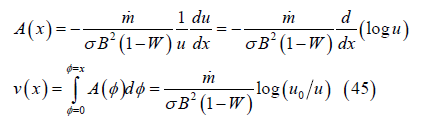
Sonic velocity, mach number, local electrode voltage and integrated current: The local sonic velocity and Mach number are
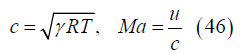
The local voltage difference ΔV between the electrodes is given in terms of the local electric field
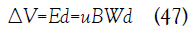
The local current density is
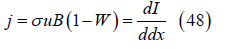
where dI is the differential current passing between the electrodes in a slice of the gas with cross sectional area d2 and axial thickness dx. Then the current flowing between the electrodes from the channel inlet to axial position x is
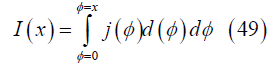
Note also that the local power per unit volume is
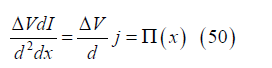
Channel design
Baseline parameters and objectives: It is assumed that the oxygen/ silver nanoparticle gas mixture exits the converging/diverging nozzle at one atmosphere pressure with velocity 1000 m/s and temperature 1000 K. Then the MHD channel inlet conditions are
• p0=1 atm
• T0=1000 K
• u0=1000 m/s
The large inlet velocity and hence large inlet kinetic energy is critical
for high MHD power output in view of Eq. (16). The difficulty
in attaining large nozzle exit velocity with heavy nanoparticles
(N >> 1) has been noted before and therefore it is implicitly
assumed here that the mixture encompasses nanoparticles of
modest size. Specific values of N are considered in the course of
the channel design, below. The gas mixture is assumed to have
87.5 mole percent silver nanoparticles (yAgN=0.875, 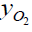 =0.125)
in order that a large gas electrical conductivity is possible and the
magnetic field in the channel is assumed to be maintained with
permanent magnets or superconducting electromagnets. Hence
the following constant values are assumed for the gas conductivity
and the magnetic field throughout the calculations:
=0.125)
in order that a large gas electrical conductivity is possible and the
magnetic field in the channel is assumed to be maintained with
permanent magnets or superconducting electromagnets. Hence
the following constant values are assumed for the gas conductivity
and the magnetic field throughout the calculations:
σ=106 S/m
B=2 T
Main objectives in the channel design are:
Design objectives
1. High conversion of gas kinetic energy to MHD power
2. Low conversion of gas kinetic energy to enthalpy
3. Modest gas temperature rise in channel (material limitations)
4. Compact channel dimensions (length and exit cross section)
5. Modest to large electrode voltage differential
In achieving these objectives the nanoparticle size N is critical since this strongly affects the mixture molecular weight, density and specific heat. Very large nanoparticles result in very high-density gas with high inertia, which requires, in turn, a long channel to decelerate the stream and convert the stream kinetic energy to MHD power. Also, a very high density gas mixture for a given mass flow rate results in a small channel cross section and small electrode separation which, in combination with the electric field E ≤ u0BW, results in low electrode voltage. Further, the large molecular weight which results for N >> 1 leads to very small mixture specific heat, Cp [J/kg-K]. For a mixture with 12.5% oxygen and nanoparticles with N=20 silver atoms per nanoparticle the mixture specific heat is 12.03 J/kg-K compared to 1143 and 193 J/kg-K for pure oxygen and silver vapor, respectively. The very low mixture specific heat causes a rapid and undesirable rise in gas temperature along the channel as part of the gas kinetic energy is converted to enthalpy.
The loading factor W at which the MHD generator operates is also critical since this parameter determines how the conversion of gas kinetic energy is partitioned between MHD power and enthalpy rise. The local power density Π(x) is greatest for W=0.5, cf. (3), which is expected to result in the optimal power density for the channel overall. However, the effective conversion of kinetic energy to MHD power rather than enthalpy requires values of W closer to unity as shown by Eqs. (16) and (18). Conversely, a channel operating with W very near unity maximizes the channel power output but W~1 also strongly reduces the Lorentz force which is proportional to (1-W). The result of this is the need for a highly elongated channel to fully decelerate the gas and provide nearcomplete conversion of kinetic energy to MHD power.
The baseline parameters used in the design are tabulated in Table
1. Note that N=40 silver atoms per nanoparticle and W=0.95 are
used as baseline values for the nanoparticle size and loading factor.
The mixture molecular weight corresponding to 12.5% oxygen
mole fraction and N=40 is M=3.781 kg/mol and the corresponding
mixture specific heat is 6.020 J/kg-K. Variations of nanoparticle
size and loading factor from these baseline values will be explored
in order to optimize channel operation. In all calculations the mass
flow rate is assumed to be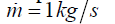 .
.
| p0 | 1 atm | yO2 | 0.125 | m! | 1 kg/s |
|---|---|---|---|---|---|
| T0 | 1000 K | s | 106 S/m | N | 40 |
| u0 | 1000 m/s | B | 2 T | W | 0.95 |
Table 1: Baseline parameters.
Baseline design: The variations of gas velocity, temperature and
density with axial position x in the channel are shown in Figure 5 corresponding to the baseline parameters. Also plotted in Figure
5 are the MHD power output from the channel inlet to x (PMHD),
the cross sectional area A, and the channel width/height d. At the
inlet the gas density is 46.1 kg/m3 and the channel cross section
is only A0=0.217 cm2 corresponding to the channel width/height
d0=4.7 mm. The sonic velocity at the inlet is 58.9 m/s and the
Mach number is 17.0 owing to the large molecular weight of the
gas (3.781 kg/mol). Also, at the inlet the Lorentz force opposing
the flow is 200 N/cm3 and the power density is Π0=190 kW/cm3.
Because of the large Lorentz force the flow decelerates rapidly and
is arrested only about 7.27 cm (xArrest) downstream of the channel
inlet. In the neighbourhood of xArrest the channel cross section
A and width/height d both increase without bound. The MHD
power generation between the channel inlet and the arrest position
is 475 kW, which is 95% (W=0.95) of the inlet kinetic energy flux
2
0 μu02 = 500 kW . However, this power output cannot be realized
because the rate of gas enthalpy rise 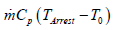 is 25 kW (Eq.
(18)) and because of the very low mixture specific heat (owing to
the large nanoparticles) the predicted temperature TArrest, ignoring
dissociation and specific heat variation, is more than 5100 K. In
order to limit the gas temperature to 2000 K, the channel length, according to Figure 5, must be no greater than about 2 cm. And,
the MHD power output between the inlet and x=2 cm is only about
114 kW. For the baseline parameters, operation with the loading
factor W=0.95 results in strong conversion of kinetic energy to
MHD power and modest conversion to enthalpy, however, the
large nanoparticles (N=40) and low specific heat results in extreme
gas temperature rise in the channel, which severely limits channel
length and power output.
is 25 kW (Eq.
(18)) and because of the very low mixture specific heat (owing to
the large nanoparticles) the predicted temperature TArrest, ignoring
dissociation and specific heat variation, is more than 5100 K. In
order to limit the gas temperature to 2000 K, the channel length, according to Figure 5, must be no greater than about 2 cm. And,
the MHD power output between the inlet and x=2 cm is only about
114 kW. For the baseline parameters, operation with the loading
factor W=0.95 results in strong conversion of kinetic energy to
MHD power and modest conversion to enthalpy, however, the
large nanoparticles (N=40) and low specific heat results in extreme
gas temperature rise in the channel, which severely limits channel
length and power output.
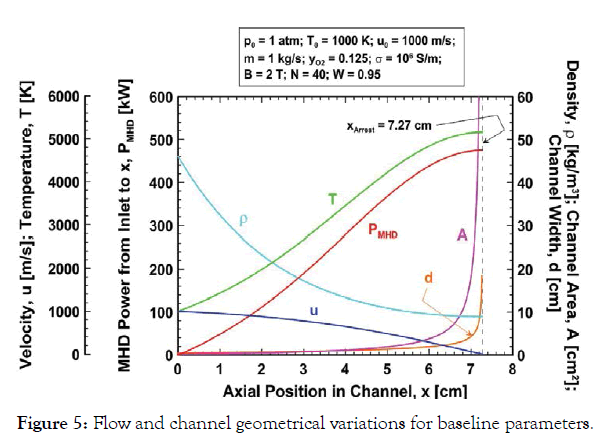
Figure 5:Flow and channel geometrical variations for baseline parameters.
The electrical parameter variations are plotted in Figure 6 for the baseline parameters. At the channel inlet the electric field, electrode voltage and current density are 1900 V/m, 8.85 V and 10,000 A/cm2, respectively. The voltage varies strongly with axial position in the channel, increasing to more than 13 V and then reducing to zero where the flow is arrested, whereas the current density reduces monotonically in proportion to the velocity. The accumulated current flow between the electrodes from the channel inlet to the arrest location is ~ 41.68 kA.
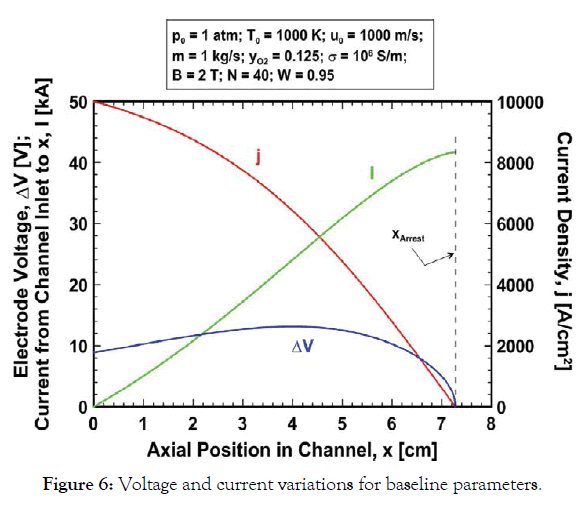
Figure 6:Voltage and current variations for baseline parameters.
Nanoparticle size (n) effects: The influence of nanoparticle size on the expansion is shown in Figure 7 which shows the velocity, temperature and MHD power variation with axial position in the channel for the baseline parameters and mixtures with N=20, 40 and 80 silver atoms per nanoparticle. The molecular weights and specific heats for these three mixtures are 1.892, 3.781 and 7.557 kg/mol, and 12.03, 6.02 and 3.01 J/kg-K, respectively. Note that the heavy/dense gas with large nanoparticles (N=80) and greater inertia is decelerated more slowly than the lighter gases. The gases are arrested at 5.30, 7.27 and 9.33 cm from the inlet for N=20, 40 and 80, respectively. The more rapid deceleration for small N results in a stronger enthalpy rise for the lighter mixture owing to more rapid conversion of kinetic energy to enthalpy. This does not, however, result in a commensurately stronger temperature rise for the lighter gas since the specific heat is greater for smaller N and this more than compensates for the greater enthalpy rise resulting in lower temperature rise for the lighter gas (Figure 7). The MHD power produced from the channel inlet to gas arrest is the same, 475 kW, for each gas because the inlet velocities/kinetic energies are the same for each. However again, this power cannot be realized because the large gas temperature rise limits the useful length of the channel well short of the length for arrested flow. The predicted temperatures at gas arrest are 3078, 5152, and 9300 K for N=20, 40, 80, respectively. In any case, because of the greater deceleration the conversion of kinetic energy to MHD power at any axial position is greatest for lighter gases (Figure 7). This also means that small N (smaller nanoparticles and lighter gas mixtures) is favourable for extracting the maximum power from the channel with fixed, limited gas exhaust temperature. If the gas exhaust temperature is 2000 K then the gas exits the channel at roughly 2 cm from the inlet for each gas mixture with velocities 720, 871, and 938 m/s and MHD power extractions of 229, 115 and 57 kW for mixtures with N=20, 40, and 80 silver atoms per nanoparticle, respectively. Although the case N=20 yields the greatest power this channel design is very inefficient since less than half of the 475 kW of kinetic energy which can theoretically be converted to MHD power is actually extracted.
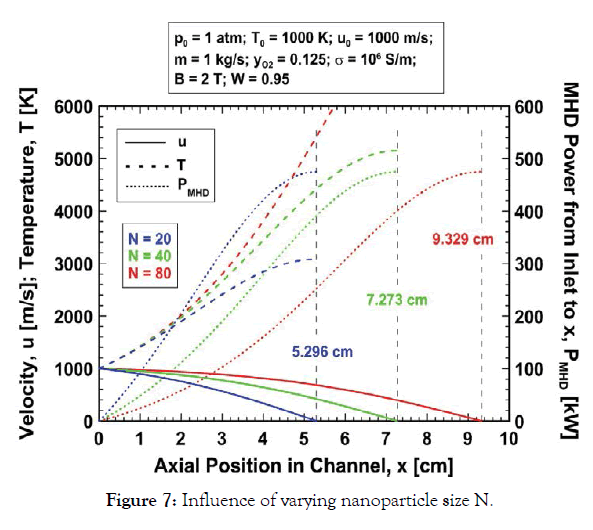
Figure 7:Influence of varying nanoparticle size N.
Loading factor (W) effects: The effect of load factor W, on the expansion is shown in Figure 8 where the variations of u, T and PMHD are plotted for the baseline parameters and the three loading factors W=0.90, 0.95 and 0.98. The gas is decelerated more rapidly for smaller W because the Lorentz force is proportional to the factor (1–W). The flow is arrested 2.33, 7.27 and 29.35 cm from the channel inlet for loading factors W=0.90, 0.95 and 0.98, respectively. Increasing W to near unity has two important effects. First, the fraction of the gas kinetic energy which is converted to MHD power (W) is greater (Eq. (16)). Therefore, for a given downstream gas velocity, PMHD is greater for larger W. But just as important, for larger W the fraction of gas kinetic energy which is converted to enthalpy (1–W) is smaller, and therefore the gas temperature rise is smaller. These two factors enable considerably larger power extraction for a fixed channel exhaust temperature when W is nearer to unity. The data in Figure 8 are re-plotted in Figure 9 with a focus on the first 15 cm of the channel. Note from Figure 9 that for an exhaust temperature of 2000 K the gas exits at about 0.5, 2, and 14 cm from the channel inlet with the approximate velocities 938, 871 and 631 m/s and MHD power extractions 54, 115 and 295 kW for the loading factors W=0.90, 0.95 and 0.98, respectively. Although the channel length for a fixed exhaust temperature is greater for larger loading factor the power output is significantly greater.
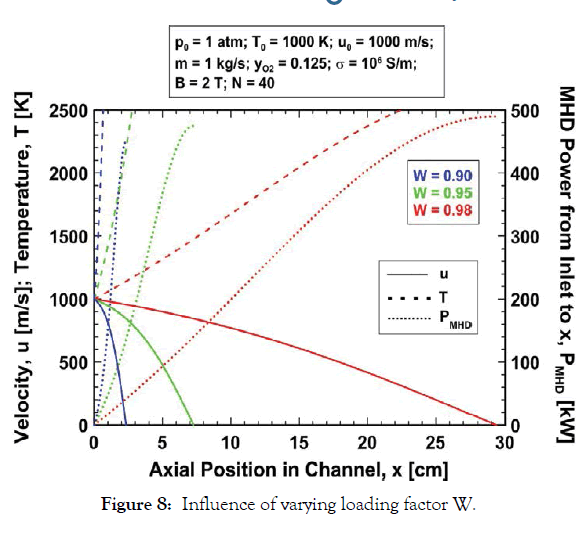
Figure 8:Influence of varying loading factor W.
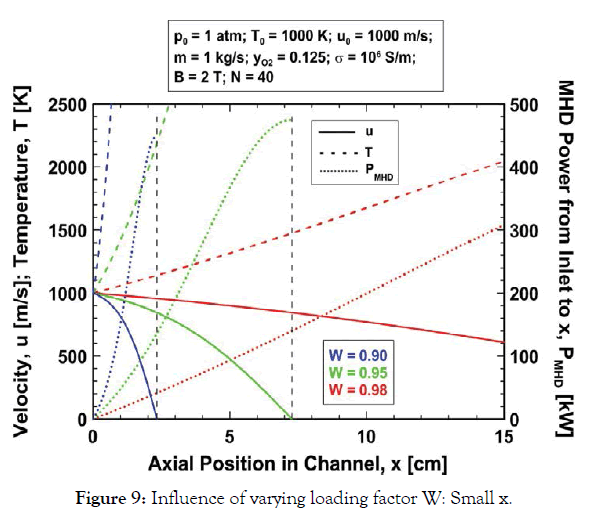
Figure 9:Influence of varying loading factor W: Small x.
Near-optimal design: N=20, W=0.98: Important flow, power and geometrical variables are plotted in Figure 10 versus axial position for the baseline parameters but with N=20 and W=0.98. This combination of nanoparticle size and loading factor was found to result in efficient conversion of kinetic energy to MHD power in a relatively compact channel with modest gas temperature rise.
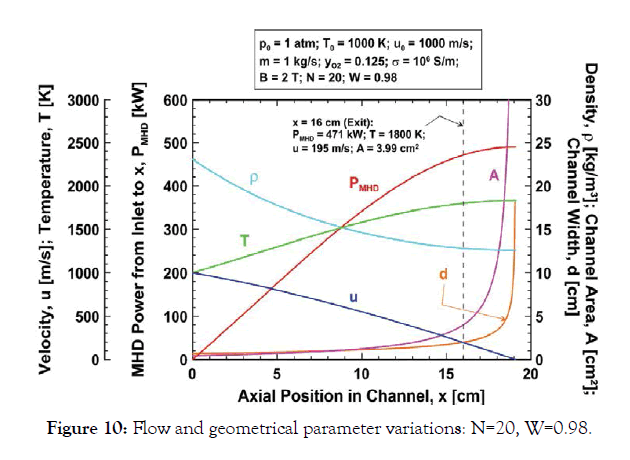
Figure 10:Flow and geometrical parameter variations: N=20, W=0.98.
The gas mixture, with density 23.1 kg/m3, enters the channel with inlet cross section A0=0.434 cm2 and width/height d0=6.59 mm. The power density and Lorentz force at the inlet are Π0=78.4 kW/ cm3 and FL0=80 N/cm3, respectively. The gas experiences relatively modest deceleration from the inlet velocity, 1000 m/s, because the loading factor W=0.98 results in a reduced Lorentz force. If the channel length was extended the gas would arrest at 19.1 cm from the inlet with temperature 1831 K and MHD power extraction 490 kW. The unbounded channel cross section at this position is avoided by limiting the channel length to 16 cm. Then, the gas exits the channel (x=16 cm) at 195 m/s and 1800 K with density 12.81 kg/m3 through a 3.99 cm2 cross section corresponding to the channel width/height d=20.0 mm. The MHD power extraction from the channel is 471 kW. This is about 96% of the 490 kW maximum theoretical extractions that would occur if the channel length was extended to completely arrest the flow. Because the volume of the 16 cm long channel is 20.4 cm3, the 471 kW MHD power output corresponds to 23.1 kW/cm3 power density. This compares very favourably to about 30 kW/litre for state of the art high-speed heavy-duty diesel engines (e.g., MAN D2862).
The distribution of the various electrical parameters in the channel corresponding to the expansion in Figure 10 is plotted in Figure 11. The electric field between the electrodes reduces monotonically from 19.6 V/cm at the channel inlet to about 3.8 V/cm at the exit (x=16 cm) and the electrode voltage ranges from 12.9 V at the inlet to a maximum of about 13.2 V at x=3.71 cm to 7.66 V at the exit. The average electrode voltage in the channel is about 11.5 V despite the narrow electrode spacing of 6.6 to 20 mm. The current density decreases monotonically in proportion to the velocity reduction and the total current flow across the channel is about 38.9 kA. The electric field, electrode voltage and current flow for the near-optimal design parameters differ only slightly from the baseline values.
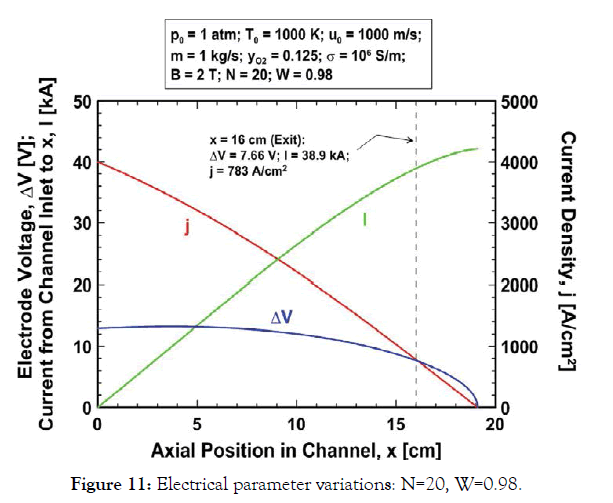
Figure 11:Electrical parameter variations: N=20, W=0.98.
Shorter arrest length for larger initial velocity: Figure 12 shows the gas velocity, temperature and density variation with x in the channel for the baseline parameters and the inlet velocities u0=1000 and 2000 m/s. Note that the flow with greater inlet velocity requires a considerably smaller distance to arrest than the flow with smaller initial velocity. This counter-intuitive result is due to the nonlinear nature of the differential equations for momentum and energy conservation which arises through the temperature dependence of the density. It is not due simply to the larger Lorentz force acting in the case of larger inlet velocity. This is clear from momentum conservation for a constant density working fluid. For constant density flow, the velocity decays linearly with distance along the channel, and the distance required to arrest the flow increases with the inlet velocity:
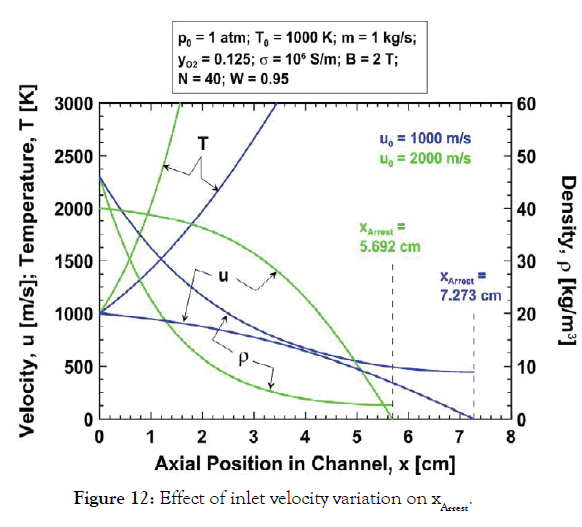
Figure 12:Effect of inlet velocity variation on xArrest.
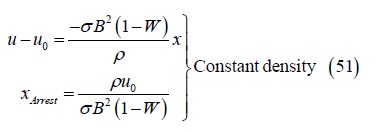
However, when density is inversely proportional to temperature the arrest distance decreases with increasing u0, for the following reasons. From momentum conservation the rate of velocity decrease with distance du/dx is initially the same for u0=1000 and u0=2000 m/s. However, the rate of kinetic energy decrease with distance is greater for larger u0. Hence kinetic energy is converted to enthalpy at a greater rate and so temperature increases more rapidly with distance for larger u0, in agreement with Figure 12. And, because temperature increases more rapidly the density (proportional to 1/T at constant pressure) decreases more rapidly for larger u0, as in Figure 12. Then, from momentum conservation, the deceleration du/dx is inversely proportional to the density so the deceleration must be greater for larger u0, which further increases the enthalpy and temperature, further reducing the density, and so on. This process gives rise to the very strong deceleration seen in Figure 12 for u0=2000 m/s. It is the nonlinear coupling between velocity and density through the temperature that results in a shorter arrest length for larger inlet velocity.
Return electromagnetic pump power
The relatively trivial pump power Ppump for the 1 kg/s silver aerosol
flow that can provide 471 kW of electricity is given by the product of the mass flow  , times the reaction chamber pressure P of 5 × 105 N/m2 (Eq. (2)),
divided by the density ρ of silver 10.5 g/cm3:
, times the reaction chamber pressure P of 5 × 105 N/m2 (Eq. (2)),
divided by the density ρ of silver 10.5 g/cm3:
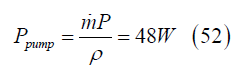
The equations of motion are solved for the particular case of an ideal gas mixture of oxygen and silver nanoparticles expanding at constant pressure in a channel with square cross section. The results indicate that nanoparticle size and the loading factor are very important parameters for maximizing the extraction of MHD power. Very large nanoparticles result in a highly dense gas mixture which requires large channel length for flow deceleration and conversion of kinetic energy to power. Large nanoparticles also greatly reduce the specific heat of the mixture which results in undesirable extreme temperature rise along the channel. The loading factor of 1/2 maximizes the local MHD power density in the channel, however, loading factors nearer to unity result in greater kinetic energy conversion to MHD power. Loading factors very near unity, however, reduce the opposing Lorentz force on the gas resulting in weak deceleration and large channel length. Parameter studies indicate those nanoparticles with 20 silver atoms per nanoparticle and a loading factor of 0.98 leads to high power extraction from a reasonably compact channel with modest gas temperatures. Calculations were carried out for a flow rate of 1 kg/s, a gas conductivity 106 S/m, a uniform magnetic field of 2 T, and inlet pressure, temperature, and velocity equal to 1 atm, 1000 K and 1000 m/s, respectively. These parameters result in the extraction of 471 kW of MHD power from a 16 cm long channel with 4 cm2 maximum cross section and gas exit temperature of 1800 K wherein the heat inventory is recovered by gas absorption in molten silver. The silver is recycled with insignificant power using electromagnetic pumps having no moving parts. The channel volume is 20.4 cm3 so the corresponding MHD power density is about 23.1 kW/cm3 (23.1 MW/litre) which compares very favourably with typical power densities in the range of only about 30 kW/litre for state-of-the-art high-speed heavy-duty diesel engines. The channel electrode voltage ranges from about 13 to 7.7 V over the 16 cm channel span and the total current flow between the electrodes is about 38.9 kA. Since the MHD efficiency may approach W=1 (0.98 in this example), the electrical conversion of the power of the plasma into electricity may approach the efficiency of pressurethermal to kinetic energy conversion wherein nozzle efficiencies of 99% have been realized.
S. Mhatre, R. Gandhi, and Y. Lu are acknowledged for measurements of oxygen absorption and silver nanoparticle formation rates.
Citation: Mills RL, Nansteel M (2019) Oxygen and Silver Nanoparticle Aerosol Magnetohydrodynamic Power Cycle. J Aeronaut Aerospace Eng, 8:216.
Received: 17-Jul-2019 Accepted: 06-Aug-2019 Published: 09-Aug-2019
Copyright: © 2019 Mills RL, et al. This is an open access article distributed under the term of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.