Journal of Defense Management
Open Access
ISSN: 2167-0374
ISSN: 2167-0374
Research Article - (2014) Volume 4, Issue 1
This analysis examines the use of a hybrid multi-attribute decision making approach, AHP & TOPSIS, to rank order the nine phases of a terrorist attack based upon data from twenty-one different terrorist attacks. Applying statistical tools to examine frequencies, we use these frequencies to gain insights into the terrorist activities. We apply the real data and criterion weights from pairwise comparisons in order to rank order the phases of a terrorist attack. Previous, just using AHP we found that terrorist training, networking, planning, and operational prep make up over 65% of the ranking weights. Using TOPSIS we found the top four ranked ordering as Operational Prep, Recruitment, Terrorist training, and terrorist Networking that accounts for over 76%. This analysis provides counterterrorism operators with keys to look for in intelligence gathering for terrorist activities.
Keywords: Terrorist attacks; Phases; TOPSIS; AHP; Multi-attribute decision making
Do terrorist attacks follow an observable pattern in their preattack activities? If there is a pattern, how reliable is it? Can we use this pattern as an indicator or warning of imminent terrorist activity? More specifically, can we use these indications and warnings to predict the timing of a future terrorist attack? [1].
The above quotation illustrates one of the many difficult situations decision makers and Counter Terrorist Operators (CTO) face in combating global terrorism. Securing Americans against terrorist attack within the United States and abroad is a difficult task and requires a methodology that assists the decision makers in their decision making. The United States and its allies are facing international challenges such as rogue states and non-state actors (i.e. terrorists). These challenges threaten peace and stability worldwide. Those challenges, coupled with sluggish economies worldwide have created a need to focus limited resources on the appropriate facets of national defense. Unlike state actors, terrorist are not limited by international diplomatic constraint. As such, the question remains: can a terrorist attack be identified prefacto?
We seek to add a new quantitative aspect to Freeman et al.’s [1] work by utilizing multi-attribute & multi-criterion principles using a combination of Analytical Hierarchy Process (AHP) and Technique of Order Preference by Similarity to ideal Solution (TOPSIS) to interpret the raw data into a more focused understanding of which phases of a terrorist attack to focus our intelligence collection efforts upon. We will briefly discuss AHP, TOPSIS, and provide the scope and limitations of its process. We explain the methodology utilized in the completion of this work. We present our outcomes of the work.
TOPSIS
The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) is a multi-criteria decision analysis method, which was originally developed in a dissertation by Hwang and Yoon in 1981 [2]. It has been further developed by Yoon [3], and Hwang, Lai and Liu [4]. TOPSIS is based on the concept that the chosen alternative should have the shortest geometric distance from the positive ideal solution and the longest geometric distance from the negative ideal solution. It is a method of compensatory aggregation that compares a set of alternatives by identifying weights for each criterion, normalizing the scores for each criterion and calculating the geometric distance between each alternative and the ideal alternative, which is the best score in each criterion. An assumption of TOPSIS is that the criteria are monotonically increasing or decreasing. Normalization is usually required as the parameters or criteria are often of incompatible dimensions in multi-criteria problems. Compensatory methods such as TOPSIS allow trade-offs between criteria, where a poor result in one criterion can be negated by a good result in another criterion. This provides a more realistic form of modeling than non-compensatory methods, which include or exclude alternative solutions based on hard cut-offs.
TOPSIS Background
TOPSIS was the result of work done by Yoon and Hwang [2]. TOPSIS has been used in a wide spectrum of comparisons of alternatives including: item selection from among alternatives, ranking leaders or entities, remote sensing in regions, data mining, and supply chain operations. TOPSIS is chosen over other methods because it orders the feasible alternatives according to their closeness to an ideal solution [5].
Napier [6] provided some analysis of the use of TOPSIS for the department of defense in industrial base planning and item selection. For years the military used TOPSIS to rank order the systems’ request from all the branches within the service for the annual budget review process [7] as well as being taught again in as part of decision analysis. Current work is being done to show the ability of TOPSIS to rank order nodes of a dark or social network across all the metrics of social network analysis [7-9].
In manufacturing analysis, Wang et al. [10] proposed two methods to improve TOPSIS for multi-response optimization using Taguchi’s loss function. Ozturk and Batuk [11] used TOPSIS for spatial decisions and then linked to Geographical Information Systems (GIS) operations for flood vulnerability. Olson and Wu [12] have shown how TOPSIS may be used for data mining and analysis in credit card score data. Olson presented a comparison of weights (centroid weights, equal weights, and weights by linear regression) in TOPSIS models using baseball data where their conclusion is that accurate weights in TOPSIS are crucial to success.
In a business setting it has been applied to a large number of application cases in advanced manufacturing processes [13,14] purchasing and outsourcing [15,16], and financial performance measurement [17].
In social networks, TOPSIS has been used to rank order the nodes across all metrics in order to identify the most influential node [9].
We only desire to briefly discuss the elements in the framework of TOPSIS. TOPSIS can be described as a method to decompose a problem into sub-problems. In most decision, the decision maker has a choice among several to many alternatives. Each alternative has a set of attributes or characteristics that can be measured, either subjectively or objectively. The attribute elements of the hierarchal process can relate to any aspect of the decision problem-tangible or intangible, carefully measured or roughly estimated, well- or poorly-understood-anything at all that applies to the decision at hand.
TOPSIS Methodology
The TOPSIS process is carried out as follows:
Step 1
Create an evaluation matrix consisting of m alternatives and n criteria, with the intersection of each alternative and criteria given as xij, giving us a matrix (Xij)mxn.
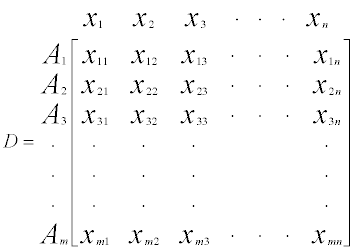
Step 2
The matrix shown as D above then normalized to form the matrix R=(Rij)mxn, using the normalization method
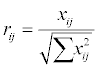
for i=1,2…m; j= 1,2,…n
Step 3
Calculate the weighted normalized decision matrix. First we need the weights. Weights can come from either the decision maker or by computation.
Step 3 a.
Use either the decision maker’s weights for the attributes x1,x2,…... xn or compute the weights through the use Saaty’s [18] AHP’s decision maker weights method to obtain the weights as the eigenvector to the attributes versus attribute pair-wise comparison matrix.
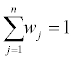
The sum of the weights over all attributes must equal 1 regardless of the method used.
Step 3 b.
Multiply the weights to each of the column entries in the matrix from Step 2 to obtain the matrix, T.
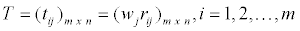
Step 4
Determine the worst alternative (Aw) and the best alternative (Ab): Examine each attribute’s column and select the largest and smallest values appropriately. If the values imply larger is better (profit) then the best alternatives are the largest values and if the values imply smaller is better (such as cost) then the best alternative is the smallest value.
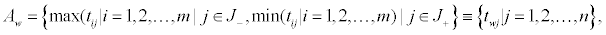
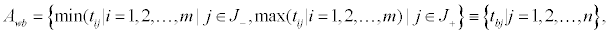
Where,
J+={j=1, 2…n|j} associated with the criteria having a positive impact, and
J-={j=1, 2...n|j} associated with the criteria having a negative impact.
We suggest that if possible make all entry values in terms of positive impacts.
Step 5
Calculate the L2-distance between the target alternative i and the worst condition Aw
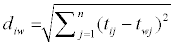
for, i=1, 2…m
and the distance between the alternative i and the best condition Ab
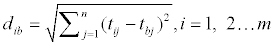
Where diw and dib are L2-norm distances from the target alternative i to the worst and best conditions, respectively.
Step 6
Calculate the similarity to the worst condition:
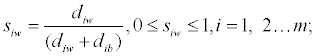
Siw=1 if and only if the alternative solution has the worst condition; and
Siw=0 if and only if the alternative solution has the best condition.
Step 7
Rank the alternatives according to their value from Siw (i=1, 2… m).
Normalization
Two methods of normalization that have been used to deal with incongruous criteria dimensions are linear normalization and vector normalization.
Linear normalization can be calculated as in Step 2 of the TOPSIS process above. Vector normalization was incorporated with the original development of the TOPSIS method , and is calculated using the following formula:
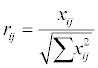
For i=1,2…m; j= 1,2,…n
In using vector normalization, the non-linear distances between single dimension scores and ratios should produce smoother tradeoffs.
Rank the alternatives according to
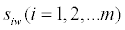
Let’s explore two options for the weights in Step 3a using AHP. First, the decision maker might actually have a weighting scheme that they want the analyst to use. In not, we suggest using Saaty’s 9-Point pair-wise method developed for the Analytical Hierarchy Process (AHP) [18]. We briefly describe this pair-wise method to obtain weights.
We might build a numerical representation using a 1-9 point scale in a pairwise comparison for the attributes criterion and the alternatives. The goal is to obtain a set of eigenvectors of the system that measures the importance with respect to the criterion. The resulting eigenvectors are the weights provided the results are consistent with a Consistency Ratio (CR) less than or equal to 0.1 [18]. We can put these values into a matrix or Table 1 based on the following:
| Intensity of Importance in Pair-wise Comparisons | Definition |
|---|---|
| 1 | Equal Importance |
| 3 | Moderate Importance |
| 5 | Strong Importance |
| 7 | Very Strong Importance |
| 9 | Extreme Importance |
| 2,4,6,8 | For comparing between the above |
| Reciprocals of above | In comparison of elements i and jif i is 3 compared to j,then jis 1/3 compared to i. |
| Rational | Force consistency; measure values available |
Table 1: Numerical representation of weights using Pair-wise comparisons.
Phase targeting methodology
According to Freeman et al [1], there are nine phases leading up to a terrorist attack. They are: Networking, Terrorist Training, Planning, Recruitment, Financing, Operational Planning, Weapons Procurement, Logistical Preparation, and Operational Preparation. Which of these are best to focus counter terrorist and intelligence collection efforts upon? Should intelligence collection efforts expend their limited amount of resources on all of them simultaneously? Such unguided action seems likely to produce inconclusive results, and a high degree of post-facto analysis on why the attack was not prevented. Which phase to focus can upon be identified, and the TOPSIS is one method to help determine a result among the phases. Numerous constraints are involved in any decision to focus efforts, for example budgetary constraints, infrastructure, capability, etc. The purpose of this study is to provide a possible method that culls the field of options while fulfilling the operational need.
Twenty-one of the twenty-four attacks were utilized in the TOPSIS, because they provided the best data to convert into a binomial analysis for implementation into the TOPSIS. The other three attacks were incomplete in terms of the phases so we left them out of the analysis. The independent variable includes 72 months of data per attack prior to the individual strikes by terrorist actors. The dependent variables are the various phases. When compiled and diagnosed by Freeman et al., [1] a noticeable trend was discerned; however, their study admits that outliers exist. Furthermore, the specific targeting of phases has been identified by other authors, such as Treverton [19]. In his work, Treverton [19], notes the importance of visibility in the focus of efforts to detect terrorist activity. Two specific examples cited are recruitment and training.
In order to complete the analysis, the process requires the establishment of the key components outlined in the introduction. The objective is to identify a ranking of the phases that provide the most effective operational targeting by national intelligence services. Second, the criteria are analyzed: the independent variable is identified (time before the attack) and the dependent variables are converted from nine different qualitative phases into a binomial distribution that could help to establish the head to head pairwise comparison for application of obtaining the decision weights via the AHP & TOPSIS using the nine point scale later in the analysis.
To provide a basis of comparison, the data is analyzed simply. Table 2 lists the phases from most common to least common when taken as a percentage of sheer occurrences in the data. Decision makers utilizing this simple approach are intuitively led to a possible false decision. Logistical Preparation, Operational Planning, and Weapons Procurement appear to be the most likely phases to be identified, and should therefore be targeted. However, once multi-attribute decision making methods are applied to the data, a new pattern emerges. The new pattern will be discussed in greater detail later in this paper.
| Phase | Relative Frequency | Rankings |
|---|---|---|
| Networking | 9.7% | 8 |
| Terrorist Training | 6.5% | 9 |
| Planning | 11.1% | 5 |
| Recruitment | 10.2% | 7 |
| Financing | 11.1% | 5 |
| Operational Planning | 13.0% | 2 |
| Weapons Procurement | 12.5% | 3 |
| Logistical Prep. | 14.4% | 1 |
| Operational Prep. | 11.6% | 4 |
Table 2: Original Phase Manifestation Percentages.
The first step in the TOPSIS method is identifying the matrix, D. The matrix D has nine rows, each row corresponding to one of the nine phases. We have twenty one columns where each column represents a terrorist attack for which we have data. Statistical analysis provides a simple technique to obtain possible values for the matrix, D. We point out that other methods exist to provide inputs for the matrix, D.
The next major step in the use of TOPSIS for this study is establishing the criterion weights for the attacks. We used the twenty one attacks to be compared pairwise in order to obtain criterion weights. For credibility, both special forces and special operations military officers aided in the pairwise decision weights efforts The matrix pits the 21 phases against one another with a specific weight for each phase within each attack. Initially, we ran the analysis assuming that each attacks was equally weighted (1/21=0.04762). Table 3 is presented as the results when equal weights are used showing the final results with respective percent and cumulative percentages.
| Phase | Percent | Cumulative Percent | |
|---|---|---|---|
| 1- Networking | 0.20962 | 0.07396 | 1 |
| 2- Terrorist Training | 0.23939 | 0.08446 | 0.842214688 |
| 3- Planning | 0.31499 | 0.11113 | 0.647381321 |
| 4- Recruitment | 0.2376 | 0.08383 | 0.926043237 |
| 5- Financing | 0.31577 | 0.11141 | 0.536249808 |
| 6- Operational Planning | 0.31283 | 0.11037 | 0.757753396 |
| 7- Weapons Procurement | 0.41207 | 0.14538 | 0.296416112 |
| 8- Logistical Prep. | 0.42808 | 0.15103 | 0.151031312 |
| 9- Operational Prep. | 0.364 | 0.12842 | 0.424840428 |
Table 3: TOPSIS Analysis using equal weighting per criteria.
Next, we apply a more modeling based method to obtain the criterion weights. The comparison is based upon a two filter processes. This comparison provides weighting to the phases in relation to their actual effects in each attack. The first filter is the frequency each phase has within a specific attack (Figure 1). The second filter mechanism is a weighted head to head pairwise comparison using the AHP pairwise comparison method applied to how each phase undergoes based upon the raw data analysis for all 216 phase manifestations out of the twentyone attacks.
Figure 1: Madrid, 2004, is an example of the data captured and placed into the AHP. The frequency of each phaseis critical in assessing the final equilibrium value achieved for each specific phase. The phases in their original order: 1-Networking; 2-Terrorist Training; 3-Planning; 4-Recruitment; 5-Financing; 6-Operational Planning; 7-Weapons Procurement; 8-Logistical Preparation; 9-Operational Preparation.
In order to obtain the 216 manifestations of the 21 attacks the raw data were analyzed binomially. When a phase manifested within any of the 21, attacks anywhere along the 72 month time period prior to an attack, it received a value of one. Next, each phase was weighted in accordance with the percentage of times it manifested in the 21 attacks to establish the quantitative basis of the data (Table 4).
| Phase | Frequency | Phase Weight (AHP) | Phase Frequency | Weights |
|---|---|---|---|---|
| Networking | 21 | 3 | 14-17 | 1 |
| Terrorist Training | 14 | 1 | 18-21 | 3 |
| Planning | 24 | 5 | 22-25 | 5 |
| Recruitment | 22 | 5 | 29-31 | 7 |
| Financing | 24 | 5 | 9 | |
| Operational Planning | 28 | 7 | ||
| Weapons Procurement | 27 | 7 | ||
| Logistical Prep. | 31 | 9 | ||
| Operational Prep. | 25 | 5 | ||
| Total | 216 |
Table 4: Weighting for each of the phases to establish the Head to Head filtering criteria.
Original Frequency AHP Phase Weight
Each individual attack is then separated from the whole of the data, and a binomial distribution was determined for each phase leading to a terrorist attack. Figure 1 is an excerpt from the data analyzed; the al- Qaeda inspired Madrid Train Bombings in 2004 provides an example of the information complied for each attack [1]. As depicted by the graph, the frequency of data collected for each phase is along the Y-axis, and the numeric code number for each phase is along the X-axis. One important note, the original phase numbers have no correlation to any weighting; furthermore, the original phase numbers are a product of the work done by Freeman et al. [1], and their depiction of the general order the phases follow from start to finish.
Each phase within each attack is then filtered in the manner explained above and are placed into a 9 × 21 matrix using Excel. This represents the D matrix. The TOPSIS steps, shown earlier, are then employed using Excel.
Our TOPSIS worksheet provided a ranking of the nine phases based upon our creation of the D matrix and the weighting scheme used (Table 5). We include present and cumulative percentages as well. The top four, Planning, Recruitment, Financing, and Logistical Prep account for over 81%.
| Phase | Percent | Cumulative Percent | |
|---|---|---|---|
| 1- Networking | 0.01571 | 0.00679 | 1 |
| 2- Terrorist Training | 0.07586 | 0.03281 | 0.97131 |
| 3- Planning | 0.61033 | 0.26397 | 0.26397 |
| 4- Recruitment | 0.52134 | 0.22549 | 0.48946 |
| 5- Financing | 0.47237 | 0.2043 | 0.69376 |
| 6- Operational Planning | 0.10634 | 0.04599 | 0.9385 |
| 7- Weapons Procurement | 0.1758 | 0.07604 | 0.89251 |
| 8- Logistical Prep. | 0.28372 | 0.12271 | 0.81647 |
| 9- Operational Prep. | 0.05063 | 0.0219 | 0.99321 |
Table 5: TOPSIS ranked output with unequal weights.
In previous work, we strictly used the AHP process for the entire analysis with Thompson’s weighting scheme [20]. We provide Table 6 as a comparison to these approaches and weighting schemes.
| Phases | AHP Ranking and Percentage | TOPSIS Ranking, Unequal Weights | TOPSIS Equal Weights | |
|---|---|---|---|---|
| Networking | 2 | 16.4% | 9 | 9 |
| Terrorist Training | 1 | 27.6% | 7 | 7 |
| Planning | 3 | 11.3% | 1 | 5 |
| Recruitment | 6 | 7.9% | 2 | 8 |
| Financing | 5 | 8.5% | 3 | 4 |
| Operational Planning | 7 | 7.2% | 6 | 6 |
| Weapons Procurement | 8 | 6.1% | 5 | 2 |
| Logistical Prep. | 9 | 4.9% | 4 | 1 |
| Operational prep. | 4 | 10.1% | 8 | 3 |
Table 6: Comparison of the Approaches.
One way to penetrate the information advantage maintained by the terrorist, which is truly maintenance of the strategic and tactical elements of surprise, is to develop a methodology of maximizing its targeting efforts. The unequal weights used in the TOPSIS model concluded, in order of precedence, the phases of Planning, Recruitment, Financing, and Logistical Preparation as the most important phases of the nine on which to focus targeting efforts. Indeed, these four phases account for approximately 82% when we normalize their TOPSIS values for the ranks. This represents a significant portion when compared to the other five phases combined.
The twenty-first century has just begun, from its inception the new threat to the international status quo for peace is not war mongering nation states bent on world domination. Quite the contrary, the biggest threat to peace worldwide is international terrorism by entities like al- Qaeda and Hezbollah. The WMD commission update highlights the threat of nuclear, biological, and chemical threats in correlation with WMDs. Rogue states with malign interests and lacking a technical delivery method may seek alternative deployment means, in the form of terrorism, to implement their international agendas, though this point is debated amongst scholars [21].
Detecting such a terrorist attack before it occurs is essential and exponentially more difficult when efforts are unfocused and misaligned. In his work, Intelligence for an Age of Terrorismm Treverton [19] explains the use of Bayesian analysis to develop strategy during the Cold War. The use of statistical processes for decision making is no less applicable now and provide an excellent point of departure when considering economy of force. Treverton [19] also explains the importance of uniqueness and visibility in developing strategy. While intuition tells us that Logistical Preparation, Weapons Procurement, and Operational Planning may be the most detectable due to their post facto manifestation, the use of the AHP & TOPSIS forces us to rethink our priorities when focusing funding and resources towards the detection of terrorist attacks.
Based upon the AHP & TOPSIS conducted for this study, Planning was the most likely phase to manifest itself before an attack occurred. While the quantitative analysis provides a percentage output against the other phases it does not indicate how successfully targeting any one phase will likely be. Therefore, the CTO must be careful when relying solely on quantitative analysis for decision making.
Since the AHP & TOPSIS utilized in this study identified Planning as the most detectable phase, a thought experiment for how a CTO would operationalize this realization. The CTO, having full confidence that the weights provided in the process are accurate to the situation, makes a decision backed by the process to focus his or her efforts on Planning followed by Recruiting. The CTO then utilizes all available means of intelligence gathering focused on these top phases. The two in concert provide a metaphorical notch and front sight post for the counter terrorist operator’s targeting picture of the terrorist threat- as the two phases align and are collected upon a framework on which to base the intelligence situation is created. While our enemies are not as apparent as they were during the World Wars or the Cold War, they are not as amorphous as presumed. The use of the AHP & TOPSIS lends focus to the collection effort and provides a framework to reference the threat situation.
A second experiment provides perspective to the model. This experiment assumes a model, which feeds real time data and updated consistently. The continuous process provides the CTO with a dynamic analytic process that demonstrates phases in the terrorist attack cycle as it evolves. Utilizing the AHP & TOPSIS in this manner allows the CTO to monitor the terrorist threat, and since the methodology is codified as a tool, the terrorist’s tactics, techniques, procedures, and strategies become a known- rather than unknown variable in the process. Each action taken by the terrorists creates a manifestation, which creates another data point to further strengthen the quantitative trend analysis. Regardless of the terrorist’s success or failure, the data is validated and the model only becomes stronger.
This work’s identified the most important phases to target; in as much as more data is created through intelligence gathering— especially as collection efforts become more refined and reliable- CTOs will witness trends changing. Such evolution provides the CTO with an increase in situational awareness, rather than increased factorials, which have no place and only, generate confusion. Similarly, as trends are analyzed and depicted in the AHP, achieving a clear situational picture provides modern day CTOs with results enjoyed by the likes of Roosevelt and Churchill when utilizing Operations Magic and Ultra, respectively [22]. The proposition to provide such situational understanding is not out of the realm of possibility, and should not be discounted because of the underdeveloped nature of the study. Quite the contrary, the stakes are high enough that an AHP approach to understand, the situation should be further studied and refined. According to Crenshaw [23] …terrorism is a form of surprise attack outside the context of war, it usually takes time to identify and locate the perpetrators. By the time the government acquires convincing evidence of a responsibility, the public’s outrage may have dissipated and justifying a punitive response will be difficult. However, responding quickly without conclusive information will likely appear clumsy and vindictive. Crenshaw’s observation validates the need for a usable, quantitative tool.
The AHP & TOPSIS is a good tool for directing study of complex problems, and provides a quantitative starting point for strategy when used in conjunction with case study, other quantitative and qualitative means, and real world intelligence fusion. The AHP is not a panacea for determining which phases are the most detectable, and as different salient points come to light, different phases are likely to manifest themselves as the harbingers of an attack. The importance of this work is not to determine which phase is universally critical; rather this work seeks to provide one more assessment tool to make the terrorist picture more clearly in a fog of unanalyzed data.
Governments need tools to anticipate attacks. The AHP & TOPSIS developed for this study is one possible tool that, given the proper attention, could simplify strategic choices. The AHP & TOPSIS conducted edifies a statement made by Treverton [19] in Intelligence for an Age of Terrorism: “For indicators, visibility is also critical.” He continues,
…terrorist planning, for instance, will be invisible to intelligence until long after the fact, left in terrorist staging areas, or available only with luck…
With the right tools and focus, the CTO can rely less on luck and more on modern data collection. The AHP & TOPSIS conducted by this work determined that Planning and Recruitment are the two most likely phases to be detected. This study validates some of Treverton’s assumptions concerning recruitment. Finally, the outcomes identified in this work provide another added benefit; These top four of Planning, Recruitment, Financing, and Logistical Preparation provide the CTO with the most time to follow the terrorist’s progress in the development of their attack—having the correct focal point can provide insight into other options and connected events, thereby perpetuating the reliability of the tool and the subsequent increase to the CTOs attack prevention capabilities.
The authors thank the reviewers for their comments which help in the revision of this paper.