Journal of Agricultural Science and Food Research
Open Access
ISSN: 2593-9173
ISSN: 2593-9173
Research Article - (2016) Volume 7, Issue 1
Phosphorus (P) losses through tile drained systems in agricultural landscapes may be causing persistent eutrophication problems observed in surface water. The purpose of this paper is to evaluate the state of the science in the Agricultural Policy/Environmental extender (APEX) model related to surface and tile P transport. This was accomplished using data from a monitored corn-soybean rotation field in the St. Joseph River watershed, IN. The estimation of soluble phosphorus (SP) in surface runoff and tile flow in APEX includes a user defined linear (based on GLEAMS) and nonlinear (Langmuir) sorption option. The results suggest that the inclusion of the Langmuir isotherm improved (18%) SP sorption estimates in surface runoff during the corn year only when P inputs were added, whereas the linear method was more appropriate during the soybean year when no fertilizers were applied. Similarly, SP estimates in tile flow were improved (30%) when using the Langmuir option during the corn year, though the overall model performance predicting this variable were very poor. Modeling improvements of P partitioning processes in APEX can help predict more realistic outputs. Yet to achieve this in tile flow, water percolation processes need to be improved to reflect preferential flow conditions often found in long-term no-till fields and in soils with high clay content. Greater accuracy in the estimation of the effect of artificial drainage systems, common in the US Midwest, should result in the improved evaluation of agricultural conservation practices in order to examine strategies that could reduce P losses for water quality purposes.
<Keywords: Adsorption; Hydrological modeling; No-till; Water quality
Phosphorus (P) from non-point sources such as agricultural lands can have a major environmental impact on the quality of receiving waters. In artificially drained agricultural fields, P losses have been considered a fraction of that in the surface, and these account for a small amount of the fertilizer application [1]. However, small P concentrations (between 0.03 to 0.06 mg/L) in water bodies can result in algal blooms and subsequently in eutrophication and hypoxic conditions [2]. The management of P on agricultural lands with hydrological pathways to sensitive receiving surface water bodies is therefore fundamentally important. Models that estimate the effects of agricultural conservation practices on water quantity and quality are increasingly important tools for short- and long-term assessments [3-5]. Due to the time and financial resources needed to adequately monitor P transport to receiving waters, simulation models have served as a valuable management tool. One such tool is the Agricultural Policy/ Environmental extender Model (APEX) [6]. APEX is an extension of the Environmental Policy Integrated Climate (EPIC) model which was developed to assess the impact of erosion productivity [6,7], and later expanded to allow for the simulation of many agricultural management processes for field-sized areas, up to 100 ha [4,8]. The major components of EPIC are weather, hydrology, sedimentation, nutrient cycling, pesticide fate, crop growth, tillage, economics, and plant competition. APEX was developed to extend EPIC functions to whole farms and small watersheds and to include routing of nutrients, pesticides, water and sediment across landscapes (e.g., fields or subareas), through shallow groundwater, and into channel systems to a watershed outlet [9]. APEX has been used to assess the effectiveness of conservation practices and is one of few models capable of simulating the routing of chemical pollutants and water at the field scale [10]. Because APEX is able to consistently model various land management strategies at scales ranging from field to farm to small watersheds, it was adopted by USDA NRCS for the Conservation Effects Assessment Program (CEAP) national assessment [11]. Recent updates to the APEX model include the simulation of soluble phosphorus (SP) transport processes from the surface to the tile drains and the inclusion of the Langmuir equation. The APEX model, similar to other models, utilizes a simplified P cycle model development by Jones et al. and Sharpley et al. [12,13] to describe soil P transformations. In APEX, following fertilizer applications, the model divides the P content into inorganic and organic pools. The inorganic pool is divided into labile, active, and stable pools. Phosphorus applications as inorganic or organic fertilizer are assumed to be in the soluble form and contribute to labile P, making the nutrient available for plant uptake. The rapid equilibrium between labile P and active P, and consequently the slower equilibrium between active P and stable P, are calculated as a function of the chemical and adsorption properties of the soil. At equilibrium, the labile P pool is proportional to the active P pool. In APEX, the labile P pool is partitioned between the solid and solution phases. Limitations of the model include the linear relationship between labile and active P pools as well as between active and stable P pools. These relationships lead to a linear relationship between solution and solid phase P pools and therefore do not reflect the nonlinear relationships of soil P sorption. Although the linear relationship may be suitable at low P soil solution concentrations, it may underestimate solution P concentrations at higher soil P concentrations which may lead to an under prediction of P in surface runoff and leaching. Applications of APEX for simulating tile drainage dynamics have been limited, likely as a result of the simplistic way in which tile flow is simulated in the model. Tile flow in APEX is a function of lateral subsurface flow and the time required for the drainage system to reduce plant stress. Although limited in use, [14] Gassman et al. evaluated APEX to simulate tile flow in the Upper Maquoketa River Watershed in northeast Iowa, and computed a satisfactory R2 value of 0.70 for average monthly tile flow. Tile flow has also been satisfactorily calibrated using the EPIC model [15,16]. Soluble P transport to tile is a function of percolation and soil properties in a given soil layer. As the water in the upper soil layer is divided to simulate runoff, evaporation, and infiltration, SP percolates to the underlying soil layer. The SP concentration percolated from the layer above is included in the SP concentration estimated for the layer in question, which is then used for estimating the losses that occur through evaporation and plant uptake. The SP nutrient transport and extraction occurs at each soil layer until it reaches the artificial drainage layer, where lateral flow results in tile flow and SP losses. The depth for each layer depends on the soil characteristics for the areas studied. Along with P modeling in tile flow, APEX was also modified to include a nonlinear P sorption algorithm, adapted from the Langmuir equation [17,18]. Inorganic fertilizer becomes readily available for leaching from the top soil layer when rainfall induced infiltration occurs. Meanwhile, it takes time for organic P to mineralize and become available for leaching. Both organic and inorganic P are subject to loss in surface runoff (soluble P and sediment-bound organic P). When inorganic P is added to soil, it has been shown that labile P and P sorption decreases in concentration [19,20]. This decline is nonlinear indicating that the P losses reach a fairly constant value. In APEX, the inorganic P flow rate did not reflect the nonlinear decrease in labile P and P sorption concentrations over time. Futhermore, the partitioning coefficient reflected linearity between the solution and the solid P phases, which is not typical of P sorption in some soils [21]. To overcome this limitation, the Langmuir adsorption isotherm was incorporated to adequately simulate environmental conditions not currently included in APEX. The inclusion of the Langmuir modification will influence the partitioning of P between soluble and adsorbed in the labile pool. It does not influence the rate of P flux to the active pool nor the partitioning between active and labile. APEX is an integral part of the evaluation of USDA conservation programs. This paper reviews the conceptual approach in APEX for estimating P losses in an artificially drained agricultural field. To help provide testing of these features the present study 1) examined the use of APEX for estimating tile flow and P losses through tile, and 2) evaluated the nonlinear P estimation (Langmuir) option as an effective method for estimating SP in surface runoff and tile flow.
General hydrology and phosphorus modeling in APEX
Hydrology: The water hydrology component in APEX is routed through channels and flood plains using a daily time step average flow, or a short interval complete flood routing method [6]. The watershed is divided into subareas (homogeneous hydrologic land-use units, HLU), and each subarea contains channel specifications. Water flow is computed from the most distant subarea to the watershed outlet. The average water flow at the outlet is a function of the water inflow volume, the area of the watershed, the frequency and duration of rainfall, and the time of concentration of the watershed above the reach. The time of concentration is dependent on the channel flow length and the average channel velocity, which is estimated using Manning’s equation [6].
Tile Drainage in APEX: Applications of APEX to simulate tile drainage dynamics have been limited. Artificial drainage systems in APEX are simulated by modifying the natural lateral subsurface flow routines [6]. Tile in APEX is simulated by indicating the depth of the drainage system and the time required (days) for the drainage system to reduce plant stress. Storage routing in APEX allows percolation of soil moisture from a soil layer when the soil water content exceeds field capacity. In APEX, surface layer is defined by a 10 mm top soil layer. Subsurface layers are typical soil layers having different properties such as texture, permeability, organic C contents, and etc. The soil layers definition and properties are often loaded from public soil databases such as STATSGO or SSURGO. The top soil layer is the hypothetical layer and its property is usually the same as the second layer, which are drawn from the database. The depth of soil layers vary by location and soil types. Water drains from one layer to the layer below as a function of storage and saturated conductivity:
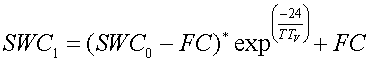 (1)
(1)
Where SWC1 and SWC0 are the soil water contents at the end and start time interval (24 hours), FC is the field capacity in mm, and TTV is the vertical travel time through a soil layer in hours. Travel time through a soil layer is calculated as:
 (2)
(2)
Where PO is porosity in mm and SC is saturated conductivity in mm h-1. The lateral subsurface flow rate (QH) is estimated in mm d-1 by partitioning the changes in soil moisture storage between vertical and horizontal flow.
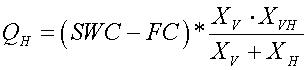 (3)
(3)
where
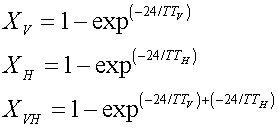
Where TTH is the horizontal travel time h. Horizontal flow is partitioned into subsurface flow to the adjacent subarea and or outflow (tile) and quick return flow. Drainage is simulated by indicating the depth of the drainage system and the time required for the drainage system to reduce plant stress. The drainage time replaces the horizontal travel time (TTH) in Equation 3 for the layer containing the system.
Phosphorus dynamics: Specific to phosphorus dynamics, APEX has two components, an organic and an inorganic P. Organic P is divided into fresh residue and stable organic P pools. Soil inorganic P is divided into active P, stable P, and labile P pools. Labile P is plantavailable P that is extracted by anion exchange resin [22] (Sharpley et al.) and represents soluble and weakly sorbed P. Studies have indicated that after an inorganic fertilizer application, labile P concentrations decrease rapidly (several days to weeks) followed by a much slower decrease in labile P which may continue for years [23,24] (Indiati et al. and Paulter and Sims). To account for the initial fast and subsequent slow decrease in labile P, APEX assumes that the labile mineral pool is in rapid equilibrium with the active mineral pool and the active mineral pool is in slow equilibrium with the stable mineral pool. The P sorption coefficient governs the equilibration between the mineral labile and active P pools. This coefficient represents the fraction of fertilizer P extracted by anion exchange resin after an incubation period 6 months [25] and is represented as:
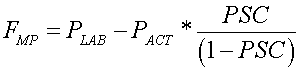 (4)
(4)
FMP is the mineral P flow rate between mineral labile and active P pools, PLAB is labile mineral P, PACT is active mineral P, and PSC is the P sorption coefficient, which is a function of physical and chemical soil properties and is described by [25] Jones et al. At equilibrium, the stable mineral P pool is four times the size of the active mineral P pool. A detailed description of the soil P model in APEX may be found in Jones et al. [3,12], Sharpley et al. and Williams et al.
In addition to the P model presented by [25] Jones et al., APEX estimates solution phase P based on the concept of partitioning mineral labile P into the solution and solid phases as described by [26] Knisel and is expressed as,
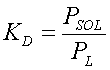 (5)
(5)
Where KD is a partitioning coefficient, PSOL is the concentration of P in the solid phase, and PL is the concentration of P in the solution phase. The default value for the partitioning coefficient is set at 100 [21].
Description of new features introduced to APEX: Though the above relationships (linear) may be suitable at low soil P concentrations, it could likely underestimate solution P at higher soil P concentrations such as in cases where there is an application of animal waste or fertilizer application in excess of plant uptake requirements. Due to this limitation, the Langmuir isotherm [18] was added to APEX to account for large soil P concentrations. At equilibrium, the Langmuir isotherm model is described as:
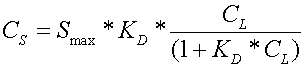 (6)
(6)
Where CS is the soluble P concentration sorbed in the soil, CL is the soluble P concentration in the liquid, and KD is a partitioning coefficient, which in APEX is the concentration of the labile P in the solid phase divided by that of the solution phase. KD is an adsorption constant related to the binding energy at equilibrium ranging from 1 to 20.
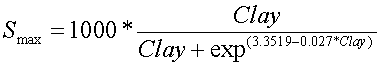 (7)
(7)
where Smax is the maximum P sorption capacity of the soil and Clay is the percentage of clay in soil layer 2. More information for this equation can be found in [27] Salton. To determine soluble P in solution we rearranged to solve for CL given CS,
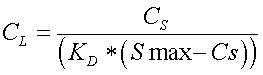 (8)
(8)
As the CS approaches Smax, the CL increases. In the current APEX model, transport of soluble P in runoff is estimated as:
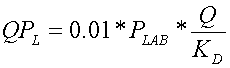 (9)
(9)
where QPL is the mass (kg ha-1) of soluble P lost in runoff volume, Q (mm) and PLAB is the concentration (g t-1) of labile P in soil layer 1. The inclusion of the Langmuir isotherm estimates soluble P in runoff (QPLAN) as:
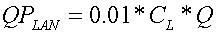 (10)
(10)
The tillage component in APEX mixes P within the top layer which is then made available for plant uptake from the root zone soil solution. Routines in APEX were added to reflect labile P in subsurface drainage and are a modification of the GLEAMS [28] (Leonard et al.) leaching component. Phosphorus leaching is expressed as a function of time, concentration, and flow rate through a soil layer using the equation
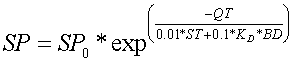 (11)
(11)
where SP0 is the initial P in solution in the soil layer (g ha-1), SP is the amount of P that remains after the amount of flow (QT) passes through a soil layer, ST is the initial water storage in mm, and BD is the bulk density. The amount of P leached by the amount of water QT is obtained by subtracting SP from SP0 using the equation
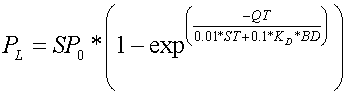 (12)
(12)
where PL is the amount of P leached by QT.
Case study-cedar creek watershed: Monitoring Site- The model simulations presented is based on edge-of-field measurements at a long-term USDA-ARS-National Soil Erosion Research Laboratory (NSERL) site in Cedar Creek sub watershed at the St. Joseph River watershed. The field is located in the northeast region of the state of Indiana (Figure 1), and has an area of 1.7 ha [29]. The predominant soil series is Glynwood silt loam, and the topography is relatively flat with a 3% slope. Corn and soybean production have been managed under notill practice for the past 25 years. A major soil limitation for row crop production in the field as well as for the Cedar Creek sub watershed is the somewhat poorly to poor drainage. As a result, tile drainage systems are placed approximately 1 meter below the soil surface to reduce saturation. The St. Joseph River watershed has been monitored by the NSERL as part of the Conservation Effects Assessment Project (CEAP) Watershed Assessment Study [30]. Surface runoff, sediment and P (total (TP) and soluble (SP)) have been collected since 2003, though data inconsistencies occured during the first few years. Tile flow and soluble P in tile (SP-tile) have been measured starting in 2008. Surface and tile discharge were collected at 10 minute intervals using a modified ISCO automated water sampler [31], while agricultural management practices were recorded by the land managers. Meteorological data (precipitation, air temperature, solar radiation, etc.) were recorded at the field site and complemented with the data collected by a nearby weather station located in Garret, IN.
Modeling parameterization: APEX model Ver. 0806 [32] was used for the present study to evaluate the inclusion of Langmuir and P leaching subroutines. The initial calibration and validation of the model for the notill site was done using an older version of APEX 0806 [33] and can be found in Francesconi et al. [32]. Due to the inclusion of more accurate input data such as fertilization dates, and upgrades to the code estimating erosion driven by runoff (Jaehak Jeong personal conversation), the recalibration of the model was conducted. The changes in the sediments values estimated using the upgraded APEX version, affected the estimation of P values as well. The subsequent recalibration and revalidation of the variables of interest was required for the present analysis. In order to recalibrate the model, several parameters including those that influence soluble P sorption capacity (PARM 8 and 96) were modified. The parameters targeted for recalibration to improve the model’s predictive capability and to test the P sorption options are listed in Table 1. Once the model was recalibrated, the P sorption linear or nonlinear equations were selected by choosing the linear (LBP = 0) or Langmuir (LBP =1) adsorption isotherm options in the command file. Tile flow estimates were also improved by removing an outlier value. A zero tile flow value was reported by NSERL’s database on May 25, 2010. However, there was a precipitation event of 48 mm that day. Given the patterns observed for tile flow compared to the amount of precipitation and antecedent soil moisture in the soil, the May 25 data point was assumed to be an error. By removing this data point the calibration of tile flow was improved from R2 = 0.42 and NS = 0.40 to R2 = 0.52 and NS = 0.45 in 2010. Model efficiency for both tile flow and surface runoff was considered satisfactory at the daily time scale (NS > 0.40). Furthermore, sediment and P in surface runoff had acceptable statistical scores (NS > 0.40) according to the standards described by Moriasi et al. [34] for a daily time step. Overall, the recalibration of APEX reasonably simulated hydrology, erosion, and P transport in surface runoff (Table 2).
| No. | Parameter | Parameter Description | Range | Value Assigned | |
|---|---|---|---|---|---|
| Initial | Final | ||||
| 1 | PARM 47 | RUSLE C factor coefficient | 0.5 – 1.5 | 1.5 | 0.5 |
| 2 | PARM 18 | Sediment routing exponent | 1.0 – 1.5 | 1.5 | 2.0 |
| 3 | PARM 76 | Standing dead fall rate | 0.0001 – 0.1 | 0.001 | 0.005 |
| 4 | PARM 18 | Sediment routing exponent | 1.0 – 1.5 | 1.5 | 2.0 |
| 5 | PARM 58 | P Enrichment ratio exponent for routing | 0.3 – 0.9 | 0.24 | 0.35 |
| 6 | PARM 57 | P Enrichment ratio coefficient or routing | 0.05 – 0.20 | 0.78 | 0.05 |
| 7 | PARM 59 | P Upward movement by evaporation coefficient | 1 – 20 | 0.5 | 1.0 |
| 8 | PARM 8 | Soluble P adsorption coefficient | 10 – 20 | 20 | 16 |
| 9 | PARM 62 | Manure erosion equation coefficient | 0.1 – 0.5 | 0.1 | 0.3 |
| 10 | LBP | Soluble phosphorus runoff estimate equation | 0 or 1 | 0 | 1 |
| 11 | PARM 96 | Soluble P leaching KD value* | 1 – 15 | 10 | 1.0 |
*Parameter modified to calibrate soluble P in tile.
Table 1: Model recalibration for utilizing APEX0806 (February, 2014) version with new routing capabilities for SP-tile and Langmuir equation.
Soluble P in surface runoff
The inclusion of the Langmuir isotherm equation and parameter (KLAN) in APEX proved to be effective at improving the estimation of P at the no-till site during the corn planting year. Compared to the calibration values produced by the linear equation, the Langmuir sorption option resulted in better calibration scores estimating TP and SP in surface runoff during 2010 (Table 2). While R2 values remained the same, NS scores improved by 18% for both TP and SP. In 2010, 4.5 Mg of manure were applied to the field prior to corn planting. In typical agricultural settings, that the same management hardly repeats every year. From the modeling standpoint, these varying inputs give dynamic and more realistic modeling environment to APEX, allowing for users to test model processes like P loads in tile drainage more realistically. This is analogous to weather input, for example, rainfall in year 1 is different from year 2 and temperature is also different day by day. If correctly implemented, changing management should be a positive point to introduce when it comes to model evaluation. The incorporation of an option in APEX that includes a maximum sorption capacity, which is based on the fraction of clay content, sets the upper limits for P binding capacity to soil particles in the top soil layer. Hence, the estimation of P takes into account the soil’s characteristics to establish a nonlinear relation between the concentration found in solution and that bound to the soil phase, which is a relationship that has been observed experimentally [35] (Sharpley). Given the nonlinear characteristics of the Langmuir equation compared to the linear method, its application may be considered when P content in the soil is relatively high. The work by Rossi et al. [21] validated the use of Langmuir to adequately simulate higher P concentration in watershed nutrient analysis using the Soil and Water Assessment Tool (SWAT). Under the high fertilizer application conditions observed at the no-till site for the year 2010, the nonlinear adsorption method would be more appropriate for estimating P losses. In addition to the fertilizer rates and the soil characteristics, other aspects of crop management may have influenced the effectiveness of the P adsorption method used in 2010. At the no-till site, the application of the manure was conducted using a surface-spread application technique. The manure was applied in mid-February while the ground was still frozen prior to planting the corn, and the type of manure used was chicken litter. Even though the nutrient composition of poultry manure varies depending on several factors (such as species, feed ratio, type of litter), P content is generally high compared to cattle manure (at about 30 – 50% that of nitrogen) [36] (Nicholson et al.). The application of chicken litter in fields that may be considered to have nutrient rich soils can result in the overapplication of P and nutrient transport to surface water [37] (Sharpley et al.). Furthermore, the application of manure fertilizers without incorporation into the soil would most likely result in nutrient losses if high precipitation events occur before crop planting takes place. Given the placement, the source, and the timing of the fertilizer application at the no-till site, high P losses could be expected. Thus a nonlinear adsorption option would better simulate P losses as was observed when using the Langmuir option in 2010. The Langmuir option was not advantageous when estimating P values under the low P conditions in 2011. On the contrary, the use of the Langmuir option made the calibration of TP and SP in runoff worse (Table 2). According to the management at the no-till site, no fertilizer applications were added during the soybeans year in 2011. The P applied during 2010 through the chicken manure application would have been taken-up by the corn crop roots, extracted in runoff, moved into the soil profile, transformed into other P pools, or degraded [25,28] (Jones et al. and Leonard et al.). The amount of labile P available for extraction into runoff in 2011 would have been greatly reduced from the topsoil layer, thus making the linear nutrient adsorption method more appropriate during the soybean year. The reduction of P in 2011 is not only observed by the monitoring data, but was also simulated in APEX (Figure 2). When using Langmuir, the P losses estimated by the model were lower compared to those observed and estimated by the linear option (Table 3). While R2 scores remained the similar for both TP and SP, NS values were slightly reduced (2%) for TP, and resulted in an error value (NS = -15) for SP. The negative NS score indicates that the observed mean would be a better predictor than the model for estimating SP in runoff [38] (Nash and Sutcliffe).
| Variable | Linear | Langmuir | ||||||
|---|---|---|---|---|---|---|---|---|
| 2010 | 2011 | 2010 | 2011 | |||||
| R2 | NS | R2 | NS | R2 | NS | R2 | NS | |
| Runoff | 0.90 | 0.84 | 0.84 | 0.79 | 0.90 | 0.84 | 0.84 | 0.79 |
| Sediment | 0.96 | 0.96 | 0.96 | 0.86 | 0.96 | 0.96 | 0.96 | 0.86 |
| Total P | 0.95 | 0.50 | 0.74 | 0.38 | 0.95 | 0.68 | 0.73 | 0.36 |
| SP | 0.93 | 0.75 | 0.58 | 0.36 | 0.93 | 0.92 | 0.58 | -15 |
| Tile Flow | 0.52 | 0.45 | 0.37 | 0.37 | 0.52 | 0.45 | 0.37 | 0.37 |
| SP-Tile | 0.17 | -1.83 | NA | NA | 0.16 | -1.28 | NA | NA |
NA = Data not available.
Table 2: APEX R2 and Nash Sutcliffe Efficiency (NS) recalibration (2010) and revalidation (2011) values.
| Observed | Linear | Langmuir | |||
|---|---|---|---|---|---|
| SP (kg/ha) | 2010 | Storm Mean | 0.030 | 0.044 | 0.031 |
| Total Annual | 0.360 | 0.524 | 0.371 | ||
| 2011 | Storm Mean | 0.009 | 0.007 | 0.002 | |
| Total Annual | 0.121 | 0.096 | 0.029 | ||
| SP-Tile (kg/ha) | 2010 | Storm Mean | 0.005 | 0.044 | 0.005 |
| Total Annual | 0.063 | 0.532 | 0.060 | ||
| 2011* | Storm Mean | N/A | N/A | N/A | |
| Total Annual | N/A | N/A | N/A |
*N/A data was not available for SP-Tile this year.
Table 3: Observed and APEX values for SP in surface runoff and SP-tile using the linear and Langmuir adsorption options for the corn (2010) and soybean (2011) years. Storm mean and total annual values were estimated for storm events during the growing season.
Soluble P in tile
Soluble P in tile is a recent nutrient routing capability in APEX. As per the modification of the subsurface lateral flow to simulate the presence of an artificial drainage system, the model has been updated to predict nutrients in tile flow. Compared to the observed data in 2010, the model results predicting SP-in tile were very poor (R2 = 0.17 NS = - 1.87). Given that no monitoring data was available for 2011, no modeling results were available for that year. The poor SP-tile prediction values in 2010 can be partly explained by the relatively low tile flow calibration scores (R2 = 0.52 and NS = 0.45). Given that the estimation of nutrients in tile depends on the accuracy of water percolation process in the soil profile, low tile flow calibration values will result in even lower nutrient prediction. Currently, tile flow modeling in APEX offers a practical, but simplified approach to measuring artificial drainage systems in agricultural fields. The predicted values provide a broad estimate of drainage flow that can be used to ensure the reasonable water balance estimation by the model during calibration, and/or to provide a rough prediction of nutrient losses through tile flow. In addition to P, APEX has also been modified to simulate N losses in tile flow. Model performance estimating this nutrient however, have been more successful. Francesconi et al. reported NS values of 0.27 for APEX estimations of N in tile flow in a corn-soybean rotation [32]. Similar to P, N losses through drainage flow in APEX are determined by estimating the change in N concentration at the soil depth where the tile is present [21]. The simulation of N in tile in APEX is derived from the EPIC model. Both EPIC and APEX incorporate various N cycle processes (i.e., nitrification, denitrification, fixation, transformation), which provide a more complex simulation of its transformation and transport to the tile compared to P. The values estimated by Chung et al. [16] using EPIC indicate a satisfactory model performance (R2 = 0.52 - 0.62 and NS = 0.43 - 0.54) when comparing monthly average N losses via tile in a corn-soybean system. Furthermore, the average monthly estimations by Gassman et al. and Saleh et al. [1,39] using APEX or a combination of APEX-SWAT, resulted in R2 values of 0.63 and 0.74 (respectively). Yet, R2 values and monthly averages are less rigorous evaluation methods than comparisons at a daily time step. Even though N routines in APEX utilize a more comprehensive approach than P, which has led to better estimations in tile drainage, N simulations have also been considered a simplified representation of this nutrient cycling process in APEX (Wang et al.) [33]. Phosphorous transfer processes from the surface through the soil profile is less understood than that of N. The tendency of P to bind to soil particles makes it mostly immobile and resistant to leaching [40] (Holford). Hence, little consideration had been given to P losses through tile as an environmental pollution problem in agriculture. In light of the persistent eutrophication processes observed, and the accumulating evidence showing P losses through artificially drained agricultural systems, attention has been brought to potential P leaching and transport mechanisms [1,24,41-43] (Breeuwsma et al., Beauchemin et al., Sims et al., Smith et al. and Gentry et al.). The observed results for P in tile flow suggest that the mechanisms by which P moves through the soil profile could be primarily associated to water percolation and preferential flow (macropore) processes. While preferential flow is not currently simulated in APEX, there is a vertical crack component that could be used for this purpose [44] (Steglich and Williams). However, this feature was not utilized in the present analysis as the relatively satisfactory tile-flow values were obtained prior to examining the P-tile model output. In the absence of a preferential flow modeling component, and disregarding the userdefined vertical soil crack characteristic, our results did not show an adequate simulation of P transport process in APEX. Given the high clay content in the St. Joseph River watershed [45], the soils are susceptible to shrink-swell conditions leading to cracking and macropores under dry conditions [46]. Macropores can also be caused by soil fauna and decomposing plant materials. The potential presence of macropores in the Midwest has been validated as an important contribution pathway of nutrients and pesticides to tile drainage systems and subsequently to ditches, streams, and lakes [47]. Furthermore, the long-term no-till management (more than 25 years) at the simulated site could result in a large number of biopores in the soil [23]. When comparing surface runoff and tile flow discharge at the field site, peak values tend to occur almost simultaneously; which is indicative of the quick water transfer from the surface to the tile [32]. In contrast, peak discharge in the tile from water percolation through the soil matrix is expected to occur following surface runoff [46]. Given that the P losses in the tile at the no-till site were associated with storm events, the main water transfer mechanism from the surface to the tile may be due to the presence of macropores. Hence, the absence of a modeling feature specific to preferential flow in APEX may be reflected in the relatively low tile flow, through satisfactory calibration score, and subsequently in the very poor SP-tile calibration results. In addition, the hydrology routine (storage-routing concept) in APEX may be less accurate than a more physically based model using the Richard’s equation when estimating water percolation through the soil matrix. Regardless of the water flow path, one could argue that the satisfactory calibration of tile flow should provide reasonable SP-tile output values. Yet, estimations of SP in tile flow in APEX are subjected to the extraction and plant uptake at each layer, which are dependent on soil characteristics. After the model was recalibrated for tile flow as well as for surface runoff, TP, and SP, the values predicted for SP-tile using the linear option for P were two orders of magnitude higher than those observed. Using the default setting for PARM 96, which modifies SPtile, the initial outputs resulted in extremely poor calibration values (R2 = 0.0 and NS = -18.0). After modifying the user defined value for SP leaching (KD) value (PARM 96 = 1) to comply with the lower SP observed in the tile, some improvements were observed (R2 = 0.16 and NS = -1.83) (Figure 3). While the calibration of tile flow can be done by modifying a few parameters (time lapse, concentration, and tile depth), it is unlikely that improvements in the prediction of this variable would result in the satisfactory estimation of SP-tile values in the present study. Given the limited dataset and the low P loads being measured, it is important to acknowledge that uncertainty in the data collection and analysis will influence the modeling results (Kavetski et al.) [14]. In addition to this potential source of error, it becomes apparent that a preferential flow component would be essential in the estimation of tile flow, as well as the need to better understand and model P dynamics to improve SP-tile predictions. While the calibration values for SP-tile were unsatisfactory using the linear method, the Langmuir option provided a reasonable approximation for the P in tile values. Despite the still very poor calibration scores using the Langmuir P adsorption option, the nonlinear model followed the trends of the observed data and in most instances it under predicted the mass of P transported through the tile (Figure 3). The results indicate that storm mean and total values during the growing season in 2010, were similar between the observed and APEX (Table 3). While the observed storm mean value was 0.005 kg ha-1 and the total annual value was 0.063 kg ha-1, the APEX predicted storm mean was 0.005 kg ha-1 and the total annual value was 0.065 kg ha-1. Given the high SP concentration in water resulting from the chicken litter application in 2010, high SP values can be expected to move from the surface to the tile layer. The effective use of the nonlinear adsorption option at the surface corresponds with the more effective use of the same method at the subsurface for estimating SP-tile. These results are promising. Even though APEX modeling of SP losses in tile will need to be further improved, prediction outputs from the current model can serve as a starting point for the generalized comparison between practices and their effect on reducing nutrient transport through artificial drainage.
Provided the satisfactory calibration of APEX for most of the variables of interest, SP-tile modeling still needs improvement. Phosphorus estimations for tile use the same analytical approach as in surface runoff. Even though the model takes into consideration the soil characteristics, as well as other important processes in the fate of P such as plant uptake, a better understanding of the main transfer mechanisms and how they interact is necessary. On the other hand, the monitoring data may have not been sufficient to adequately evaluate SP-tile outputs in APEX. A larger dataset would provide greater confidence. Despite the restrictions of the measured data and the model limitations predicting SP-tile, APEX may be on the right track simulating P dynamics in the soil. The inclusion of the Langmuir adsorption isotherm provides evidence of the model’s plasticity to adapt to environmental conditions in order to better simulate P transfer and transformation processes. Among the existing process-bases models, APEX is capable of broadly simulating tile flow and nutrient transport in tile, and can be utilized to roughly assess a variety of agricultural practices, which otherwise could not be reproducible experimentally due to cost and time constraints.