Journal of Physical Chemistry & Biophysics
Open Access

Plasmon-Induced Flexibility and Refractive Index Measurement in a Sensor Designed by a Cavity, Two Rings, Two Teeth and Two Plasmonic Waveguides

Hamid Abbasi^{* *}Correspondence: Hamid Abbasi, Department of Physics, University of Mazandaran, Babolsar, Iran, Email:

Author info »

Introduction

Surface Plasmon Polaritons (SPPs) have been studied extensively recently due to the fact that they confine light at nanoscale dimensions [1]. As a result of these unique features, SPPs are used in many structures such as filters [2], optical demultiplexers, bio-sensors [3-20], logic gates and etc. The Metal-Insulator-Metal (MIM) optical waveguide is used extensively for design of many plasmonic devices due to its ability to confine light within a small area and its compatibility with electronic platforms [21-30]. In addition, having a simple design procedure makes it one of the most favorable structures. Consequently, a diversity of MIM plasmonic devices have been designed and implemented. Some of them are optical filters, sensors, coulpers, slow light devices, splitters and all-optical switches. A good refractive index sensor needs to have a good sensitivity (S) and a high Figure of Merit (FOM). Increasing the device size usually increases the sensitivity, but larger structures have higher full width half maximum, which leads to a reduction of FOM. Many criteria can be used to implement refractive index sensors, but plasmonic sensors are more suitable for integrated circuits due to their very small size (nanometers). Recently, various types of plasmonic sensors have been designed and manufactured. Among them, plasmonic refractive index sensors require high sensitivity and resolution. Conventional plasmonic sensors consist of a MIM waveguide with a cavity. Such cavities can have a variety of geometries such as tooth-shaped, disc-shaped, ring-shaped, and so on. In this paper, we propose a MIM plasmonic sensor with two rings and a cavity and two teeth. To simulate the sensor, the two-dimensional Finite Difference Time Domain (FDTD) method with a uniform mesh size of 8 nm has been used. The boundary condition for all directions is selected as the Perfectly Matched Layer (PML).

Materials and Methods

Structural model and theory analysis

There are many structures for designing optical sensors. These optical sensors usually include amplifiers and waveguides. Each waveguide with any geometric shape has the ability to transmit waves and can limit their energy in one and two dimensions. The proposed structure is shown in Figure 1, which includes two waveguides and a cavity, and two rings and two teeth. The input wave goes from the left waveguide to the structure and after passing through them goes to the output waveguide. The width of the two waveguides is w₁=50 nm. The middle ring is located in the middle of two waveguides that have an inner radius of r₁=90 nm and an outer radius of R₁=w133 nm, which is located at a distance of 19 nm from the two waveguides. The two teeth are connected to the middle ring, which has a length of 40 nm and a height of 20 nm. A ring is located at the bottom of the right waveguide and has an inner radius of r₁=91 nm and an outer radius of R₁=126 nm. The cavity also has a length of L=80 nm and a height of W₂=200 nm. The lower ring is attached to the waveguide and the cavity and the distance from the cavity to the waveguide is 55 nm. P_in and P_out are the monitors for measuring the input and output waves, respectively, and the transmission is calculated by T=P_out/P_in.

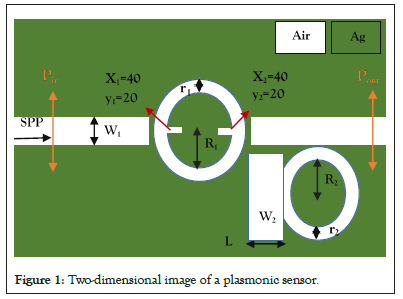
Figure 1: Two-dimensional image of a plasmonic sensor.

As shown in the 2D image, the green and white areas represent silver and air, respectively. The air permittivity is set to ε=1 and the silver permittivity is used using the greeting model as follows:

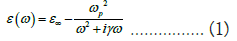
Here c_∞ gives the medium constant for the infinite frequency, ω_p refers to bulk frequency for plasma, γ means damping frequency for electron oscillation, and ω shows incident light angular frequency. The parameters for silver are c_∞=1, ω_p=1.37 × 1016 Hz, and γ=3.21 × 1013 Hz. Only TM mode is available in the structure. According to Figure 1, the TM wave, which is used for SPP excited waves, starts propagating from the left waveguide and propagates in the waveguide, and its intensity decreases as it gets closer to the output port. After distributing the field at the resonant frequency of the simulated structure, each amplifier reflects a certain amount of input wave.

Results and Discussion

Fracture coefficient simulation and measurement methods

The resonant behavior of the proposed structure is examined numerically and theoretically. In the numerical approach, we use the Time Domain Finite Difference (FDTD) simulation method with Perfectly Matched Layer (PML) boundary conditions because this method effectively reduces the numerical reflection. The uniform mesh size is 8 nm. First, to measure the performance of the sensor and increase its quality, we must change its refractive index. This is done in the wavelength range of 400 nm to 1500 nm and the refractive index of the middle ring will change in steps of 0.01 from 1.15 nm to 1.2 nm. An electromagnetic field is generated by the excitation of a sensing element using light generated by SP that is concentrated on the metal surface. The refractive index of the MIM changes when the material under contact contacts the sensor. SPs are very sensitive to changes in refractive index in the vicinity of the surface. The reason we have only changed the refractive index of one ring and the refractive index of other amplifiers remains the same is to achieve a better result and a stronger sensor design. The transmission spectrum from the sensor device is shown in Figure 2.

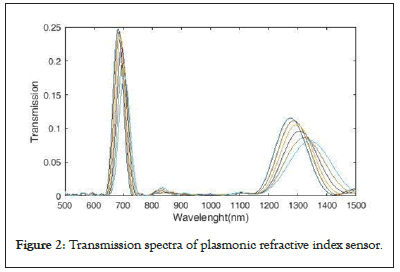
Figure 2: Transmission spectra of plasmonic refractive index sensor.

After comparing the wavelengths using the refractive index change and plotting the transmission spectrum, we must obtain the three criteria of sensitivity S and the shape of the FOM and the quality factor Q. With this, we create a technology map to define the standard and development process of optical refractive index sensors. Sensitivity S defines the ratio of the output wavelength change of the sensor to the refractive index changes and is obtained from the following relation:

S = Δλ / Δn(nm / RIU) ……………. (2)

We see the diagram of the plasmonic sensitivity coefficient in Figure 3, which according to the figure, has the highest sensitivity for the refractive index n=1.2 (in mode 2) which is equal to 2359 nm/RIU and the lowest value for the refractive index n=1.16 (in mode 1) Which is equal to 314.1 nm/RIU.

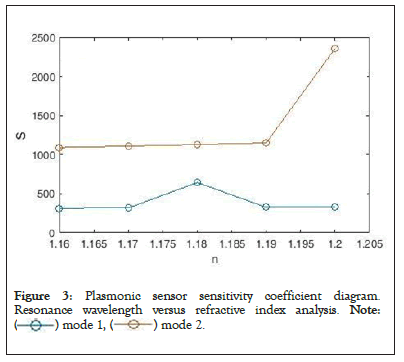
Figure 3: Plasmonic sensor sensitivity coefficient diagram. Resonance wavelength versus refractive index analysis. Note:

The next item is the Figure of Merit (FOM), which determines the sensitivity of the S_RI to the resonance width curve (FWHM) and how accurately the minimum resonance can be measured. FOM is calculated as follows:

FOM = S_RI FWHM ……………. (3)

We see the diagram of the Figure of Merit (FOM) in Figure 4, which according to the figure has the highest value for the refractive index n=1.18 (in mode 1) which is equal to 15.03 and the lowest value for the refractive index n=1.12 (in mode 1) which is equal to with 7.354.

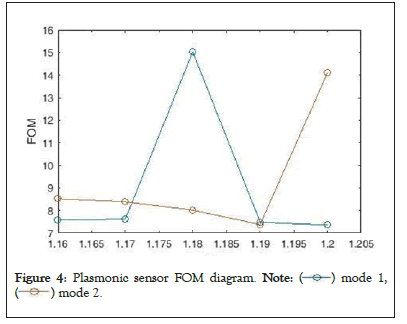
Figure 4: Plasmonic sensor FOM diagram. Note:

And the last case is the quality factor Q, which is obtained from the following equation:

Q = λ_res /FWHM ……………. (4)

We see the quality factor Q diagram in Figure 5.

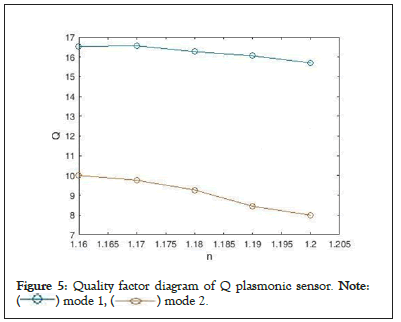
Figure 5: Quality factor diagram of Q plasmonic sensor. Note:

According to the figure, the highest value of quality factor Q is for refractive index n=1.17 (in mode 1) which is equal to 16.56 and the lowest value for refractive index is n=1.19 (in mode 2) which is equal to 7.379. These three factors (S and FOM sensitivity and Q quality factor) and their numerical values showed that this sensor has good performance and quality and has a higher sensitivity compared to similar articles.

Conclusion

In this paper, a very high resolution refractive index optical sensor is presented. It is based on plasmonic conductors of metal-metal insulation. The structure is numerically simulated using the finite difference time domain method. The proposed structure is thought to consist of two plasmonic waveguides, a cavity, two rings and two teeth. This sensor provides a sensitivity of 2359 nm/RIU and a maximum rating of 15.0316 RIU-1 (FOM). Due to its high resolution, this sensor can easily change 0.01% in the analytic refractive index for the index in the range of 1.15-1.2.

References

1. Barnes WL, Dereux A, Ebbesen TW. Surface plasmon subwavelength optics. Nature. 2003;424(6950):824-830.

   [Crossref] [Google Scholar]

2. Wu W, Yang J, Zhang J, Huang J, Chen D, Wang H. Ultra-high resolution filter and optical field modulator based on a surface plasmon polariton. Opt Lett. 2016;41(10):2310-2313.

   [Crossref] [Google Scholar] [PubMed]

3. Chen L, Liu Y, Yu Z, Wu D, Ma R, Zhang Y, et al. Numerical analysis of a near-infrared plasmonic refractive index sensor with high figure of merit based on a fillet cavity. Opt Express. 2016;24(9):9975-9983.

   [Crossref] [Google Scholar] [PubMed]

4. Tong L, Wei H, Zhang S, Xu H. Recent advances in plasmonic sensors. Sensors. 2014;14(5):7959-7973.

   [Crossref] [Google Scholar]

5. Shen Y, Zhou J, Liu T, Tao Y, Jiang R, Liu M, et al. Plasmonic gold mushroom arrays with refractive index sensing figures of merit approaching the theoretical limit. Nat Commun. 2013;4(1):2381.

   [Crossref] [Google Scholar]

6. Srivastava T, das R, Jha R. Highly sensitive plasmonic temperature sensor based on photonic crystal surface plasmon waveguide. Plasmonics. 2013;8:515-521.

   [Crossref] [Google Scholar]

7. Maisonneuve M, Kelly OD, Blanchard-Dionne AP, Patskovsky S, Meunier M. Phase sensitive sensor on plasmonic nanograting structures. Opt Express. 2011;19(27):26318-26324.

   [Crossref] [Google Scholar] [PubMed]

8. Elsayed MY, Ismail Y, Swillam MA. Semiconductor plasmonic gas sensor using on-chip infrared spectroscopy. Appl Phys A. 2017;123(1):113.

   [Crossref] [Google Scholar]

9. Cen C, Lin H, Huang J, Liang C, Chen X, Tang Y, et al. A tunable plasmonic refractive index sensor with nanoring-strip graphene arrays. Sensors. 2018;18(12):4489.

   [Crossref] [Google Scholar] [PubMed]

10. Cheng F, Yang X, Gao J. Enhancing intensity and refractive index sensing capability with infrared plasmonic perfect absorbers. Optics Lett. 2014;39(11):3185-3188.

    [Crossref] [Google Scholar] [PubMed]

11. Cheng L, Wang Z, He X, Cao P. Plasmonic nanosensor based on multiple independently tunable Fano resonances. Beilstein J Nanotechnol. 2019;10(1):2527-2537.

    [Crossref] [Google Scholar] [PubMed]

12. Chou Chao CT, Chou Chau YF, Huang HJ, Kumara NT, Kooh MR, Lim CM, et al. Highly sensitive and tunable plasmonic sensor based on a nanoring resonator with silver nanorods. Nanomaterials. 2020;10(7):1399.

    [Crossref] [Google Scholar] [PubMed]

13. Wu D, Tian J, Li L, Yang R. Plasmon induced transparency and refractive index sensing in a new type of graphene-based plasmonic waveguide. Opt Communi. 2018;412:41-48.

    [Crossref] [Google Scholar]

14. Haque E, Mahmuda S, Hossain MA, Hai NH, Namihira Y, Ahmed F. Highly sensitive dual-core PCF based plasmonic refractive index sensor for low refractive index detection. IEEE Photonics J. 2019;11(5):1-9.

    [Crossref] [Google Scholar]

15. El Shamy RS, Khalil D, Swillam MA. Mid infrared optical gas sensor using plasmonic Mach-Zehnder interferometer. Sci Rep. 2020;10(1):1293.

    [Crossref] [Google Scholar] [PubMed]

16. Esfahani Monfared Y. Overview of recent advances in the design of plasmonic fiber-optic biosensors. Biosensors. 2020;10(7):77.

    [Crossref] [Google Scholar] [PubMed]

17. Gryga M, Ciprian D, Hlubina P. Bloch surface wave resonance based sensors as an alternative to surface plasmon resonance sensors. Sensors. 2020;20(18):5119.

    [Crossref] [Google Scholar] [PubMed]

18. Ghiasi M, Mehrzad H, Mohajerani A. Sensor based on plasmonic absorption of island metal films, varying refractive index of the surrounding environment.
19. Gomez-Cardona N, Reyes-Vera E, Torres P. High sensitivity refractive index sensor based on the excitation of long-range surface plasmon polaritons in H-shaped optical fiber. Sensors. 2020;20(7):2111.

    [Crossref] [Google Scholar] [PubMed]

20. Kanso M, Cuenot S, Louarn G. Sensitivity of optical fiber sensor based on surface plasmon resonance: Modeling and experiments. Plasmonics. 2008;3:49-57.

    [Crossref] [Google Scholar]

21. Maier SA. Plasmonics: Fundamentals and applications. New York: Springer; 2007.

    [Crossref] [Google Scholar]

22. Wu T, Liu Y, Yu Z, Peng Y, Shu C, Ye H. The sensing characteristics of plasmonic waveguide with a ring resonator. Opt Express. 2014;22(7):7669-7677.

    [Crossref] [Google Scholar] [PubMed]

23. Yan SB, Luo L, Xue CY, Zhang ZD. A refractive index sensor based on a metal-insulator-metal waveguide-coupled ring resonator. Sensors. 2015;15(11):29183-29191.

    [Crossref] [Google Scholar]

24. Huang YX, Xie YY, Zhao WL, Che HJ, Xu WH, Li X, Li JC. A plasmonic refractive index sensor based on a MIM waveguide with a side-coupled nanodisk resonator. In 2014 IEEE 20^th International Conference on Embedded and Real-Time Computing Systems and Applications. 2014:1-5.

    [Crossref] [Google Scholar]

25. Wu T, Liu Y, Yu Z, Ye H, Peng Y, Shu C, et al. A nanometeric temperature sensor based on plasmonic waveguide with an ethanol-sealed rectangular cavity. Opt Commun. 2015;339:1-6.

    [Crossref] [Google Scholar]

26. Tang Y, Zhang Z, Wang R, Hai Z, Xue C, Zhang W, et al. Refractive index sensor based on Fano resonances in metal-insulator-metal waveguides coupled with resonators. Sensors. 2017;17(4):784.

    [Crossref] [Google Scholar] [PubMed]

27. Zhang Z, Luo L, Xue C, Zhang W, Yan S. Fano resonance based on metal-insulator-metal waveguide-coupled double rectangular cavities for plasmonic nanosensors. Sensors. 2016;16(5):642.

    [Crossref] [Google Scholar] [PubMed]

28. Zafar R, Salim M. Enhanced figure of merit in Fano resonance-based plasmonic refractive index sensor. IEEE Sens J. 2015;15(11):6313-6317.

    [Crossref] [Google Scholar]

29. Zhao X, Zhang Z, Yan S. Tunable Fano resonance in asymmetric MIM waveguide structure. Sensors. 2017;17(7):1494.

    [Crossref] [Google Scholar] [PubMed]

30. Chen J, Li Z, Zou Y, Deng Z, Xiao J, Gong Q. Coupled-resonator-induced Fano resonances for plasmonic sensing with ultra-high figure of merits. Plasmonics. 2013;8:1627-1631.

    [Crossref] [Google Scholar]