Pharmaceutical Analytical Chemistry: Open Access
Open Access
ISSN: 2471-2698
ISSN: 2471-2698
Research Article - (2018) Volume 4, Issue 1
Keywords: Pyrimidine compounds; Ligand complexes; Potentiometric titration; pka values; Thermodynamics
In today’s age of molecular biology purines and pyrimidines are best known as the basic constituents of the nucleic acids which are biomolecules that store genetic information in cells or that transfer this information from old cells to new one. There are two groups of nucleic acids: deoxyribonucleic acid and ribonucleic acid, DNA and RNA, respectively [1]. The nitrogenous bases fall into two classes: purines and pyrimidines. Barbituric acid derivatives are a well-known class of compounds, many of which are widely used as drugs having such disparate pharmacological activities as depressants, hypnotics and stimulants [2].
A spectrophotometric method [3] for the determination of drugs containing aromatic amino group (derivatives of p-aminobenzoic acid and sulfanilic acids) was based on the drug reaction with 5-nitrobarbituric acid in DMF [4]. Additionally, liquid membrane electrode systems responsive to the nicotinium cation were described based on the use of the ion-association complexes of this cation with 5-nitrobarbiturate counter anions in nitrobenzene solvent as ionexchange sites [5].
Methods of argentometric potentiometric titration of uracils were developed with the use of ion-selective electrodes, where an ethanolic sample solution was titrated versus aqueous AgNO3 in a medium of borate buffer (pH 9.3-9.8) using a silver-selective Ag2S electrode versus SCE. A potentiometric titrimetric method [5] for the determination of 2-mercaptopyrimidine and thiouracil derivatives was based on the reaction with K2Cr2O7 and back-titration with FeII. Masoud et al. [6-14] studied the solution chemistry of different pyrimidine compounds by potentiometric and spectral methods. The data were explained from different views; pKs, electronic character of substituent and solvation. pkai and thermodynamic parameters for BA, PB, NBA and TU by using potentiometric titration technique were given.
The potentiometric titration procedure was applied to evaluate the dissociation constants of the organic ligands as barbituric acid, 5-nitrobarbituric acid, phenobarbital and 2-thiouracil. The metal ions used are: Zn2+, Cd2+, Hg2+, VO2+, Pd2+, Y3+, Ce3+ and Sm3+. The metal contents were determined as reported [15]. Cole-Parmer pH meter was calibrated before and after each series. The correction factor was calculated using standard buffers (pH’s 4.0, 7.0 and 9.0). The potentiometric titration was proceeding by introducing an appropriate volume of the organic compound (5 ml 10-2 M) into the titration cell in presence of 5 ml of 0.5 M KCl solution as a supporting electrolyte and complete the volume to 50 ml by adding water or 50% (v/v) dioxanewater media.
The solution in the titration cell was titrated against standard KOH at controlled ionic strength and constant temperatures (25-40°C). The same potentiometric titration experiment was used for studying the complex equilibria in aqueous media or in 50% (v/v) dioxane-water media as follows: The complex solution (1 ml 10−2 M metal ion+5 ml 10−2 M ligand+5 ml 0.5 M KCl+39 ml water or 50% (v/v) dioxanewater) was titrated against standard KOH. The experiment was done under the same conditions discussed for the free organic compounds.
The potentiometric titration studies were done in aqueous media and in 50% (v/v) dioxane-water media at different temperatures (25- 40°C).
The studies were applied for the following
Evaluation of dissociation constants of the ligands, Determination of stability constants of the complexes.
Evaluation and discussion of thermodynamic parameter values.
The application of the potentiometric measurements depends on evaluation of the average number of the protons associated with the reagent, 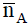 , based on the following equation [16]:
, based on the following equation [16]:
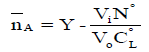
Vi: is the volume of alkali required to reach a given pH on the titration curve; Vo: is the initial volume of the ligand. No: is the alkali concentration; CLo : is the total concentration of the ligand; Y: is the number of displaceable hydrogen atoms in the ligand; The pKai values for different ligands are calculated and collected in Table 1.
| Method |  - pH - pH |
Point-wise | Algebraic | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperature | 25°C | 30°C | 35°C | 40°C | 25°C | 30°C | 35°C | 40°C | 25°C | 30°C | 35°C | 40°C | |
| Ligand | Media | ||||||||||||
| Barbituric acid | aqueous | 4.29 (9.96) |
3.95 (9.96) |
3.86 (9.64) |
3.78 (9.51) |
4.27 (10.00) |
3.94 (9.99) |
3.86 (9.68) |
3.77 (9.55) |
4.27 (9.96) |
3.99 (9.96) |
3.82 (9.64) |
3.73 (9.52) |
| 5-Nitro-barbituric acid | aqueous | 2.93 (9.64) |
2.90 (9.44) |
2.84 (9.41) |
2.82 (9.41) |
2.92 (9.65) |
2.90 (9.45) |
2.83 (9.41) |
2.81 (9.41) |
3.30 (9.64) |
3.20 (9.44) |
2.94 (9.41) |
2.47 (9.40) |
| Phenobarbital | 50% (v/v) dioxane-water | 8.51 (11.56) |
8.39 (11.57) |
8.38 (11.42) |
8.30 (11.24) |
8.51 (11.57) |
8.39 (11.57) |
8.38 (11.42) |
8.29 (11.25) |
8.51 (-) |
8.39 (-) |
8.38 (-) |
8.29 (-) |
| 2-Thiouracil | 50% (v/v) dioxane-water | 8.45 (11.71) |
8.29 (11.62) |
8.18 (11.31) |
8.10 (11.21) |
8.44 (11.70) |
8.30 (11.64) |
8.17 (11.32) |
8.10 (11.21) |
8.45 (-) |
8.29 (11.83) |
8.18 (11.63) |
8.10 (11.29) |
Values in parentheses are due to pKa2
Table 1: The pKai values for the ligands.
From the obtained data the following conclusions are given:
Most pKai values are decreased by increasing temperature. The pKai values of 5-nitrobarbituric acid are smaller than that of barbituric acid which indicate that the acidity of the 5-nitro compound is high and can be attributed to the strong electron withdrawing nitro group.
The pKai values of phenobarbital and 2-thiouracil in 50% (v/v) dioxane-water media are mostly higher than that in aqueous media [17], due to lower ionizing power of the mixed solvent.
The scheme of ionization of barbituric acid is represented as follows:
The acidity constant in pure aqueous medium (Ka) can be related to that in water-organic solvent mixture (Ka′) by the following equation [18]:
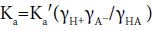
γ is the activity coefficient of the subscripted species in a partially aqueous medium to that in a pure aqueous one? The electrostatic effects of solvents operate only on the activity coefficients of charged species [18], so one can expect that the increase in the amount of the organic cosolvent in the medium will increase the activity coefficients of both H+ and A− ions. This will result in a decrease in the acid dissociation constant (high pKai value).
In addition to the electrostatic effects, the hydrogen-bonding interaction between the conjugate base (A−) and solvent molecules controls the pKai values.
The difference in the stabilization of the ionic form by hydrogen bond donor solvent molecules plays an important role for the increase in the pKai value as the organic cosolvent is added to the medium.
Thermodynamic parameters of ionization of the ligands (ΔG, ΔHo, ΔSo) were evaluated in the temperature range (25-40°C). The data are collected in Table 2. The following conclusions are given [19]:
| Ligand | DHo (kJ mol-1) | DSo (J mol-1 K-1) | DG (kJ mol-1) | |||
|---|---|---|---|---|---|---|
| 25°C | 30°C | 35°C | 40°C | |||
| BA | 58.16 (59.49) |
114.43 (7.76) |
24.06 (57.18) |
23.49 (57.14) |
22.92 (57.10) |
22.35 (57.06) |
| NBA | 13.94 (25.95) |
- 9.36 (-96.46) |
16.73 (54.70) |
16.78 (55.18) |
16.82 (55.66) |
16.87 (56.14) |
| PB | 22.91 (39.42) |
-85.75 (-90.12) |
48.46 (66.28) |
48.89 (66.73) |
49.32 (67.18) |
49.74 (67.63) |
| TU | 41.52 (64.63) |
-22.11 (- 7.86) |
48.11 (66.97) |
48.22 (67.01) |
48.33 (67.10) |
48.44 (67.09) |
Values in parentheses are corresponding to the second ionization of the ligands.
Table 2: Thermodynamic parameters of ionization of the ligands.
The positive ΔHo values indicated that the acid dissociation is accompanied by an endothermic process. The values of ΔHo for NBA
The negative ΔSo values showed that the acid dissociation is accompanied by solvation process.
The positive ΔG values revealed that the acid dissociation is nonspontaneous process and the order of ΔG values for barbituric acid and its derivatives (5-nitrobarbituric acid, phenobarbital) is as follows:
Phenobarbital>barbituric acid>5-nitrobarbituric acid.
This can be attributed to the order of acidity: 5-nitrobarbituric acid>barbituric acid>phenobarbital where the nitro group is of electron withdrawing property which increases the acidity. The ethyl and phenyl groups of phenobarbital have different opposing effects (net effect is donation) so the acidity is decreased. The comparable ΔG values for 2-thiouracil and phenobarbital are due to the acidity of them.
Equilibrium constants for the formation of complexes in solution
The average number of moles of ligand, L2−, bound per mole of metal ion present is designated by:
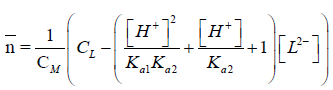
The values of pL at 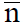 =0.5 and 1.5 are equal to log K1, and log K2, respectively.
=0.5 and 1.5 are equal to log K1, and log K2, respectively.
However, the point-wise method [16] is applied to give more concordant log K values.
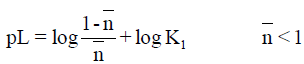
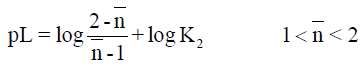
The required log Ki values for metal complexes of barbituric and 5-nitrobarbituric acids in aqueous media are collected in Tables 3 and 4. Also, log ki values for the same complexes of phenobarbital and 2-thiouracil in 50% (v/v) dioxane-water media are collected in Tables 5 and 6. All the VO2+ complexes of barbituric acid, 5-nitrobarbituric acid, phenobarbital and 2-thiouracil are of the highest stability constants. The thermodynamic parameters of the metal complexes were investigated in the temperature range (30-40°C) (Table 7).
| Metal ion | 25°C | 30°C | 35°C | 40°C | |||||
|---|---|---|---|---|---|---|---|---|---|
| log K1 | log K2 | log K1 | log K2 | log K1 | log K2 | log K1 | log K2 | ||
| M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | ||
| VO2+ | Cal. | 10.28, 10.30 | 9.54, 9.56 | 9.75, 9.75 | 8.99, 9.00 | -,9.97 | 9.12,9.11 | ||
| Aver. | 10.29 ± 0.01 | 9.55 ± 0.01 | 9.75 | 8.995 ± 0.005 | 9.97 | 9.115 ± 0.005 | |||
| Zn2+ | Cal. | 5.78, 5.99 | 5.27, 5.27 | ||||||
| Aver. | 5.885 ± 0.105 | 5.27 | |||||||
| Y3+ | Cal. | 8.38, 8.37 | 7.97, 7.93 | 7.95, 7.95 | 7.52, 7.51 | 7.76, 7.77 | 7.34, 7.29 | ||
| Aver. | 8.375 ± 0.005 | 7.95 ± 0.02 | 7.95 | 7.515 ± 0.005 | 7.765 ± 0.005 | 7.315 ± 0.025 | |||
| Pd2+ | Cal. | 8.23, 8.24 | 7.86, 7.87 | 7.94, 7.93 | 7.52, 7.52 | 7.84, 7.82 | 7.46, 7.45 | ||
| Aver. | 8.235 ± 0.005 | 7.865 ± 0.005 | 7.935 ± 0.005 | 7.52 | 7.83 ± 0.01 | 7.455 ± 0.005 | |||
| Cd2+ | Cal. | 5.08, 5.41 | 3.95, 3.97 | ||||||
| Aver. | 5.245 ± 0.165 | 3.96 ± 0.01 | |||||||
| Hg2+ | Cal. | 7.51, 7.50 | 7.13, 7.14 | ||||||
| Aver. | 7.505 ± 0.005 | 7.135 ± 0.005 | |||||||
| Ce3+ | Cal. | 7.89, 7.91 | 6.94, 7.07 | 7.18, 7.18 | 5.47, 5.59 | 7.34, 7.30 | 5.52, 5.66 | ||
| Aver. | 7.90 ± 0.01 | 7.005 ± 0.065 | 7.18 | 5.53 ± 0.06 | 7.32 ± 0.02 | 5.59 ± 0.07 | |||
| Sm3+ | Cal. | 6.79, 6.73 | 3.46, 3.48 | ||||||
| Aver. | 6.76 ± 0.03 | 3.47± 0.01 | |||||||
M1= 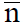 -pL method
-pL method
M2=Point-wise method, Cal.: Calculated, Aver.: Average.
Table 3: Stability constants of metal complexes of barbituric acid in aqueous media at different temperatures.
| Metal ion | 25°C | 30°C | 35°C | 40°C | |||||
|---|---|---|---|---|---|---|---|---|---|
| log K1 | log K2 | log K1 | log K2 | log K1 | log K2 | log K1 | log K2 | ||
| M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | ||
| VO2+ | Cal. | 7.58, 7.66 | 7.15, 7.15 | 7.46, 7.45 | 7.08, 7.09 | 7.45, 7.45 | 7.03, 7.01 | ||
| Aver. | 7.62 ± 0.04 | 7.15 | 7.455 ± 0.005 | 7.085 ± 0.005 | 7.45 | 7.02 ± 0.01 | |||
| Zn2+ | Cal. | 5.68, 5.72 | 4.72, 4.72 | ||||||
| Aver. | 5.70 ± 0.02 | 4.72 | |||||||
| Y3+ | Cal. | 4.69, 4.69 | 4.27, 4.24 | 4.52, 4.51 | 4.17, 4.16 | 4.70, 4.70 | 4.37, 4.36 | ||
| Aver. | 4.69 | 4.255 ± 0.015 | 4.515 ± 0.005 | 4.165 ± 0.005 | 4.70 | 4.365 ± 0.005 | |||
| Pd2+ | Cal. | 7.23, 7.32 | -, - | 6.59, 6.70 | -, - | 6.75, 6.85 | -, - | ||
| Aver. | 7.275 ± 0.045 | - | 6.645 ± 0.055 | - | 6.80 ± 0.05 | - | |||
| Cd2+ | Cal. | 4.30, 4.36 | 3.57, 3.57 | ||||||
| Aver. | 4.33 ± 0.03 | 3.57 | |||||||
| Hg2+ | Cal. | 6.25, 6.27 | 5.71, 5.72 | ||||||
| Aver. | 6.26 ± 0.01 | 5.715 ± 0.005 | |||||||
| Ce3+ | Cal. | 5.49, 5.54 | 4.52, 4.48 | 5.22, 5.21 | 4.62, 4.61 | 5.31, 5.30 | 4.74, 4.76 | ||
| Aver. | 5.515 ± 0.025 | 4.50 ± 0.02 | 5.215 ± 0.005 | 4.615 ± 0.005 | 5.305 ± 0.005 | 4.75 ± 0.01 | |||
| Sm3+ | Cal. | 3.25, 3.25 | -, - | ||||||
| Aver. | 3.25 | - | |||||||
M1= 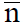 -pL method.
-pL method.
M2=Point-wise method, Cal.: Calculated, Aver.: Average.
Table 4: Stability constants of metal complexes of 5-nitrobarbituric acid in aqueous media at different temperatures.
| Metal ion | 25°C | 30°C | 35°C | 40°C | |||||
|---|---|---|---|---|---|---|---|---|---|
| log K1 | log K2 | log K1 | log K2 | log K1 | log K2 | log K1 | log K2 | ||
| M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | ||
| VO2+ | Cal. | -, - | 7.01, 6.96 | -, - | 7.40, 7.30 | -,- | 8.52, 8.27 | ||
| Aver. | - | 6.985 ± 0.025 | - | 7.35 ± 0.05 | - | 8.395 ± 0.125 | |||
| Zn2+ | Cal. | 7.78, 7.72 | -, - | 7.29, 7.14 | -, - | 6.52, 6.60 | -, - | ||
| Aver. | 7.75 ± 0.03 | - | 7.215 ± 0.075 | - | 6.56 ± 0.04 | - | |||
| Y3+ | Cal. | 10.31,10.38 | 6.20, 6.17 | 10.19, 10.24 | 6.38, 6.37 | 10.03, 10.09 | 6.55,6.54 | ||
| Aver. | 10.345 ± 0.035 | 6.185 ± 0.015 | 10.215 ± 0.025 | 6.375 ± 0.005 | 10.06 ± 0.03 | 6.545 ± 0.005 | |||
| Pd2+ | Cal. | 8.23, 8.18 | -, - | 6.08, 6.03 | -, - | -, - | -, - | ||
| Aver. | 8.205 ± 0.025 | - | 6.055 ± 0.025 | - | - | - | |||
| Cd2+ | Cal. | 5.59, 5.57 | 4.85, 4.83 | 5.39, 5.39 | -, - | 5.38, 5.39 | 4.98, 4.98 | ||
| Aver. | 5.58 ± 0.01 | 4.84 ± 0.01 | 5.39 | - | 5.385 ± 0.005 | 4.98 | |||
| Hg2+ | Cal. | 7.27, 7.24 | 5.53, 5.51 | 7.13, 7.13 | 5.20, 5.19 | 7.30, 7.29 | 5.45, 5.44 | ||
| Aver. | 7.255 ± 0.015 | 5.52 ± 0.01 | 7.13 | 5.195 ± 0.005 | 7.295 ± 0.005 | 5.445 ± 0.005 | |||
| Ce3+ | Cal. | 10.72, 10.74 | 7.35, 7.36 | 9.93, 10.13 | 7.02, 7.04 | 9.16, 9.07 | 7.26, 7.22 | ||
| Aver. | 10.73 ± 0.01 | 7.355 ± 0.005 | 10.03 ± 0.1 | 7.03 ± 0.01 | 9.115 ± 0.045 | 7.24 ± 0.02 | |||
| Sm3+ | Cal. | 5.83, 5.83 | -, - | ||||||
| Aver. | 5.83 | - | |||||||
M1=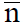 -pL method.
-pL method.
M2=Point-wise method, Cal.: Calculated, Aver.: Average.
Table 5: Stability constants of metal complexes of phenobarbital in 50% (v/v) dioxane-water media at different temperatures.
| Metal ion | 25°C | 30°C | 35°C | 40°C | |||||
|---|---|---|---|---|---|---|---|---|---|
| log K1 | log K2 | log K1 | Log K2 | log K1 | log K2 | log K1 | log K2 | ||
| M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | M1, M2 | ||
| VO2+ | Cal. | -, - | 7.94,7.89 | -, - | 8.14, 8.04 | -, - | 8.34,8.27 | ||
| Aver. | - | 7.915 ± 0.025 | - | 8.09 ± 0.05 | - | 8.305 ± 0.035 | |||
| Zn2+ | Cal. | 8.36, 8.26 | 5.28, 5.15 | 7.07, 7.03 | -, - | 7.56, 7.53 | -, 4.73 | ||
| Aver. | 8.31 ± 0.05 | 5.215 ± 0.065 | 7.05 ± 0.02 | - | 7.545 ± 0.015 | 4.73 | |||
| Y3+ | Cal. | 10.50, 10.55 | 6.54, 6.50 | 9.86, 9.90 | 6.95, 6.90 | 10.14, 10.18 | 6.94, 6.97 | ||
| Aver. | 10.525 ± 0.025 | 6.52 ± 0.02 | 9.88 ± 0.02 | 6.925 ± 0.025 | 10.16 ± 0.02 | 6.955 ± 0.015 | |||
| Pd2+ | Cal. | 5.24, 5.24 | -, - | 5.31, 5.35 | -, - | 5.53, 5.51 | -, - | ||
| Aver. | 5.24 | - | 5.33 ± 0.02 | - | 5.52 ± 0.01 | - | |||
| Cd2+ | Cal. | 9.88, 9.89 | -, - | 10.42, 10.49 | -, - | 11.11, 11.07 | -, - | ||
| Aver. | 9.885 ± 0.005 | - | 10.455 ± 0.035 | - | 11.09 ± 0.02 | - | |||
| Hg2+ | Cal. | 14.91, 14.91 | 6.41, 6.33 | -, 15.60 | 6.53, 6.46 | -, 15.39 | 6.0, 5.99 | ||
| Aver. | 14.91 | 6.37 ± 0.04 | 15.60 | 6.495 ± 0.035 | 15.39 | 5.995 ± 0.005 | |||
| Ce3+ | Cal. | 9.78, 9.83 | 6.86, 6.84 | 9.68, 9.72 | 6.95, 6.91 | 9.66, 9.70 | 7.26,7.21 | ||
| Aver. | 9.805 ± 0.025 | 6.85 ± 0.01 | 9.70 ± 0.02 | 6.93 ± 0.02 | 9.68 ± 0.02 | 7.235 ± 0.025 | |||
| Sm3+ | Cal. | 9.24,9.22 | 7.11,7.14 | ||||||
| Aver. | 9.23 ± 0.01 | 7.125 ± 0.015 | |||||||
M1= 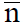 -pL method.
-pL method.
M2=Point-wise method, Cal.: Calculated, Aver.: Average.
Table 6: Stability constants of metal complexes of 2-thiouracil in 50% (v/v) dioxane-water media at different temperatures.
| Ligand | Metal ion | DHo(kJ mol-1) | DSo(J mol-1 K-1) | DG (kJ mol-1) | ||
|---|---|---|---|---|---|---|
| 30°C | 35°C | 40°C | ||||
| BA complexes | VO2+ | -58.85, (-78.74) | 0.43, (-79.08) | -58.98, (-54.78) | -58.99, (-54.38) | -58.99, (-53.99) |
| Y3+ | -111.01, (-114.62) | -206.67, (-226.75) | -48.39, (-45.92) | -47.36, (-44.78) | -46.33, (-43.65) | |
| Pd2+ | -74.64, (-74.73) | -89.12, (-96.84) | -47.63, (-45.39) | -47.19, (-44.91) | -46.74, (-44.42) | |
| Ce3+ | -106.16, (-259.36) | -201.78, (-726.53) | -45.02, (-39.23) | -44.01, (-35.59) | -43.01, (-31.96) | |
| NBA complexes | VO2+ | -31.02, (-23.60) | 43.08, (59.07) | -44.07, (-41.50) | -44.29, (-41.79) | -44.50, (-42.09) |
| Y3+ | 1.47, (19.69) | 93.56, (145.64) | -26.88, (-24.44) | -27.35, (-25.17) | -27.81, (-25.89) | |
| Pd2+ | -87.93, (-) | -153.21, (-) | -41.50, (-) | -40.74, (-) | -39.97, (-) | |
| Ce3+ | -38.52, (45.39) | -22.63, (235.91) | -31.66, (-26.09) | -31.55, (-27.27) | -31.43, (-28.45) | |
| PB complexes | VO2+ | -, (255.36) | -, (974.36) | -, (-39.87) | -, (-44.74) | -, (-49.61) |
| Zn2+ | -215.96, (-) | -563.86, (-) | -45.10, (-) | -42.29, (-) | -39.47, (-) | |
| Y3+ | -52.63, (65.39) | 24.60, (334.39) | -60.08, (-35.93) | -60.21, (-37.60) | -60.33, (-39.27) | |
| Cd2+ | -34.69, (-) | -8.22, (-) | -32.20, (-) | -32.16, (-) | -32.11, (-) | |
| Hg2+ | 6.97, (-13.27) | 161.07, (60.11) | -41.84, (-31.49) | -42.64, (-31.79) | -43.45, (-32.09) | |
| Ce3+ | -292.15, (-22.32) | -757.97, (65.58) | -62.48, (-42.19) | -58.69, (-42.52) | -54.90, (-42.85) | |
| TU complexes | VO2+ | -, (70.77) | -, (385.03) | -, (-45.90) | -, (-47.82) | -, (-49.75) |
| Zn2+ | -139.73, (-) | -307.54, (-) | -46.55, (-) | -45.01, (-) | -43.47, (-) | |
| Y3+ | -68.10, (80.27) | -26.02, (390.93) | -60.22, (-38.18) | -60.09, (-40.14) | -59.96, (-42.09) | |
| Pd2+ | 50.74, (-) | 267.48, (-) | -30.30, (-) | -31.64, (-) | -32.98, (-) | |
| Cd2+ | 217.85, (-) | 908.09, (-) | -57.30, (-) | -61.84, (-) | -66.38, (-) | |
| Hg2+ | 88.05, (-66.57) | 578.87, (-95.72) | -87.35, (-37.56) | -90.25, (-37.08) | -93.14, (-36.61) | |
| Ce3+ | -23.69, (70.59) | 109.37, (363.40) | -56.83, (-39.52) | -57.38, (-41.33) | -57.93, (-43.15) | |
Values in parentheses are corresponding to the second stability constants of the complexes
Table 7: Thermodynamic parameters of complex formation.
From thermodynamic parameters obtained for the complexes, the following conclusions are given:
Most of the complexes have negative ΔHo values which indicated that the complex formation is accompanied by an exothermic process.
Some complexes have positive ΔSo values (entropically favourable) while the others have negative So values (entropically unfavourable).
The negative ΔG values indicated that the complex formation is spontaneous process. The VO2+ complexes had the highest ΔG values.
The thermodynamic stability of the formed metal complex depends on the nature of both the acceptor (metal ion) and the donor ligand. For metal complexes where the binding between the central metal ion and the ligand donor atom is predominantly electrostatic, that is, of the ion-ion or ion-dipole type, the strongest bonds with a given ionic or dipolar ligand should be formed by those metal ions possessing large ionic potentials [20].
Thus, for a series of complexes involving closely similar metal ions and a particular ligand, the stability increases with ionic potential [21,22].
All the data typified the formation of complex compounds with different stabilities. The hard acids (metals) (VO2+, Y3+, Sm3+, Ce3+) prefer to bind with hard bases (ligands), meanwhile the soft acids (Pd2+, Cd2+, Hg2+) prefer to bind with soft bases. This statement can be used to predict qualitatively the relative stability of the metal complexes (hard acids and bases are small and non-polarizable while soft acids and bases are larger and more polarizable).
The ligands under investigation are considered to be hard bases:
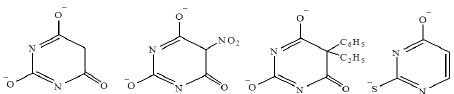
This facilitates the easier formation of the present complexes. The chelate effect plays a role in the complex stability and can be attributed to more favourable entropy changes associated with ring formation [20].
Majority of complexation reactions have isokinetic temperature (β)
Potentiometric titration studies give the dissociation constants of the ligands, stability constants of the complexes and thermodynamic parameters (ΔH°, ΔS° and ΔG) for the ligands and their complexes.
The pKai values of 5-nitrobarbituric acid are smaller than that of barbituric acid due to the strong electron withdrawing nitro group. The pKai values of phenobarbital and 2-thiouracil in 50% (v/v) dioxanewater media are mostly higher than that in aqueous media, due to lower ionizing power of the mixed solvent. All the VO2+ complexes of barbituric acid, 5-nitrobarbituric acid, phenobarbital and 2-thiouracil are of the highest stability constants. Majority of complexation reactions are entropy controlled.