Journal of Theoretical & Computational Science
Open Access
ISSN: 2376-130X
ISSN: 2376-130X
Research Article - (2015) Volume 2, Issue 2
This paper presents an analytical method used to calculate a precise value of the up and down quark masses. The method used is based on a hypothesis that elementary particles share force carrier particles with precise quantities of energy in order to bond using integer multiples of their adjusted Compton wavelengths in addition to their deBroglie momentum wavelengths. Overlapping wavelengths were found by converting mass and coupling energies into large integers using an integer based derivation of Einstein’s energy momentum equation. Both the (uud) proton and (udd) neutron structures were modeled, and the 2010 CODATA neutron-proton mass ratio was used to narrow the range of uncertainty in the quark mass calculations. The up and down quark mass search range extended from 0-6.2 MeV and 0.8-8.8 MeV respectively, with the largest common factor spike appearing within the QCD predicted values suggesting this method is valid.
u=2.24311 ± 0.00046 MeV
d=4.82977 ± 0.00046 MeV
<Less than 1% of the mass of a proton and neutron is due to the up and down quark masses, the rest come from the strong coupling force binding them together through the exchange of gluons. Due to confinement, quark masses cannot be directly measured. Quantum chromo dynamics (QCD) estimates a range of 1.8-3.0 MeV for the up quark mass and a range of 4.5-5.5 MeV for the down quark mass [1].
This paper presents a numerical method of calculating a much more precise value of the up and down quark masses. The numerical analysis is based on a first principles hypothesis that elementary particles absorb precise quantities of kinetic energy in order to bond using integer multiples of their adjusted Compton wavelengths in addition to their deBroglie momentum wavelengths. In order to facilitate the analysis of wavelength integer factors and multiples, integer based derivations of Einstein’s energy equations have been derived and shown to be mathematically equivalent to their classical counterparts [2]. This method has been used previously to calculate the exact value of the fine structure constant (FSC). One output of that analysis was the exact integer value for the mass of the proton, a key input into this analysis.
Integer based derivations used in the analysis
Einstein equated energy with mass and momentum in his famous relativistic energy momentum equation shown in Equation 1.
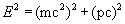 (1)
(1)
Energy (E) in Joules
Mass (m) in Kg
Speed of Light (c) 2.99792456E08 m/s
Velocity (v) in m/s
Momentum (p) mv in Kgm/s
The relativistic energy momentum equation can be written using dimension less integers by including a rest mass (nm) and a kinetic energy (nv) term. The integers can be converted to energy units by the use of Plank’s Law, where the wavelength is represented by a constant unit wavelength λu divided by the integer terms of mass(nm) and kinetic energy (nv). The total energy is simply the sum of these two unit energy units as shown in Equation 2.
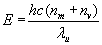 (2)
(2)
Energy (E) in Joules
Plank’s Constant (h) 6.62606896E-34 Js
Speed of Light (c) 2.99792456E08 m/s
Unit Energy Wavelength (λu )constant, in meters
Number of Rest Mass Energy Units (nm)dimensionless integer
Number of Kinetic Energy Units (nv) dimensionless integer
Einstein’s relativistic energy momentum equation, Equation 1, is in the form 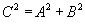 which is Pythagorean’s Theorem equating the sides of a right triangle. The two energy Equations 1 and 2 are equated by matching the sides of this right triangle as shown in Figure 1. In this case, the hypotenuse C is the total unit energy count (nm+nv), the adjacent side A is the rest mass energy count (nm), and the opposite side B can be calculated using Pythagorean’s Theorem to be
which is Pythagorean’s Theorem equating the sides of a right triangle. The two energy Equations 1 and 2 are equated by matching the sides of this right triangle as shown in Figure 1. In this case, the hypotenuse C is the total unit energy count (nm+nv), the adjacent side A is the rest mass energy count (nm), and the opposite side B can be calculated using Pythagorean’s Theorem to be 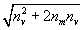 which is inversely proportional to the deBroglie Wavelength.
which is inversely proportional to the deBroglie Wavelength.
By definition, the Compton wavelength is inversely proportional to(nm), the rest mass of the particle. When a particle is in motion, this wavelength shortens and becomes inversely proportional to(nm+nv) the adjusted Compton wavelength, also referred to in this paper as the Total Energy wavelength.
Proton-electron model
The hypothesis states that elementary particles absorb precise quantities of kinetic energy in order to form integer multiples of their total energy wavelength in addition to their deBroglie wavelengths. This means that particles that bond, like the electron and proton with their respective rest masses (nme and nmp), share the same quantity of kinetic energy (nv) in order for their total energy wavelengths 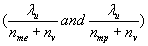 to share common factors. The quantity of kinetic energy is the same because they share a common photon with an energy value of nv. The first particle pair tested was the protonelectron pair because the Fine Structure Constant had been measured to such high precision; it allowed the
to share common factors. The quantity of kinetic energy is the same because they share a common photon with an energy value of nv. The first particle pair tested was the protonelectron pair because the Fine Structure Constant had been measured to such high precision; it allowed the  ratio to be calculated with in a very tight range using Equation 3.
ratio to be calculated with in a very tight range using Equation 3.
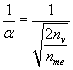 (3)
(3)
A large common factor analysis was run and documented in the paper “Exact Calculation of the Fine Structure Constant and Lepton Mass Ratios”, Brian Dale Nelson Copyright 2014 [2]. The largest common factor found between the electron and proton was 295775 with an electron multiple of 472 (Figure 2). A photon with an integer energy value(nv) of 3717 was shared between the electron and proton in order to create total energy wavelengths with a common factor this large.
Photon Energy(nv) 3717
Electron Rest Mass (nme) 139602083
Electron Total Energy (nme+nv) 139605800
Proton Rest Mass (nmp) 256330738058
Proton Total Energy (nmp+nv) 256330741775
Largest Common Factor Multiple 139605800/295775=472
256330741775/295775=866641
Plugging these values into Equation 3, the exact fine structure constant was calculated to be:
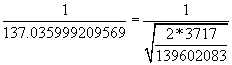 (4)
(4)
Proton-neutron model
The Standard Model confirms the proton consists of two up quarks and one down quark. The neutron consists of two down quarks and one up quark. However, the mass difference between the proton and neutron does not equal the difference between the up and down quark masses. This means the gluon energy bonding them is different in the proton and neutron. This complicated the common factor analysis when applied to this problem because the unknowns included both the two quark masses, and the two different gluon energies binding them together.
The proton and neutron energy triangles are shown in Figures 3 and 4. The proton gluon energy nvpand the neutron gluon energy nvnare shared between the three quarks. In maximizing the common factors between the total energy legs of these triangles, the uu and dd quark pairs share the same total energy therefore their highest common factor is their total energy, nmu+nvp and nmd+ nvn respectively. This represents the highest possible common factor with a multiple of one, and suggests this is why these particles contain quark pairs. The total rest mass energy in the proton (nmu) is equal to the sum of the quark masses and the gluon binding energy in the proton as shown in Equation 5:
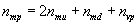 (5)
(5)
The total rest mass energy in the neutron (nmn) is equal to the sum of the quark masses and the gluon binding energy in the neutron as shown in Equation 6:
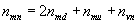 (6)
(6)
The neutron-proton mass ratio has been measured to a high degree of precision (2010 CODATA) as shown in Equation 7:
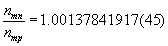 (7)
(7)
The factor analysis used large integers to search for common factors. In order to relate the large integer values to conventional measures of energy like MeV, the following conversion factor can be used that relates the proton mass integer value ( nmp) to the measured MeV energy of the proton. While the integer values of energy are exact, the MeV values are a measured approximation, even though the measured values are very precise.
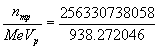 (8)
(8)
Quark-gluon common factor analysis
The key to determining the up and down quark masses was to find the largest common factors between the up and down quarks in both the proton and neutron. A computer program was written to search for the largest factors within the prescribed quark mass search ranges. The procedure included the following steps:
1) The program constants were assigned including the Proton Mass ( nmp) , and Neutron-Proton Mass Ratio. The quark mass search range was assigned.
2) The program calculated the min-max integer limits for the (nmu) up quark mass,(nmd) down quark mass, (nvp) proton gluon, (nmu+nvp) up quark total energy in the proton, and the (nmd+nvp) down quark total energy in the proton. The MeV mass ranges were converted to integer values using Equation 8.
3) The program iterated integer values within the min-max search ranges for the proton up and down quark total energy values (nmu+nvp) and (nmd+nvp).It searched for the largest common factors between these two values.
4) When a large common factor was found between the ud quarks in the proton, the min-max limits for the neutron gluon nvn was calculated using the ± 3 sigma limits of the neutron-proton mass ratio.
5) The program then iterated integer values within the min-max search ranges for the neutron up and down quark total energy values (nmu+nvn) and (nmd+nvn) .It then searched for the largest common factors between these two values.
6) When large common factors were found in both the proton and neutron quark energy triangles, these values were printed to file.
Exact values for the up and down quark masses could not be calculated because there were too many unknowns. Values for the quark masses and gluon energies can float within ranges and continue to produce the same large factors and multiples. However, very precise measurements of the Neutron-proton mass ratio limit these ranges and the subsequent uncertainties to very small values.
The computerized, large factor search algorithm used in this analysis searched a wide range of possible mass values for the up and down quarks. By definition, a factor analysis is always periodic, but large factor combinations in both the proton and neutron models with the same quark mass values are very rare. Five large factor peaks were found in a wide search range that included up quark mass values from 0 to 6.2 MeV and down quark mass values from 0.8 to 8.8 MeV. These large factor peaks are shown in Table 1. Only one large factor peak was found within the QCD predicted ranges for the up and down quark masses. In all of these cases, the mass difference between the up and down quark was found to be 2.586655(73) MeV.
| Up Quark Mass (MeV) | Down Quark Mass (MeV) | Largest Factor in Proton | Largest Factor in Neutron | Up-Down Mass Difference (MeV) |
|---|---|---|---|---|
| 0.951370008 | 3.53802555 | 706660000 | 353330000 | 2.586655541 |
| 2.244697779 | 4.83135332 | 706660000 | 353330000 | 2.586655541 |
| 3.538025550 | 6.12468109 | 706660000 | 353330000 | 2.586655541 |
| 4.831353320 | 7.41800886 | 706660000 | 353330000 | 2.586655541 |
| 6.124681091 | 8.71133663 | 706660000 | 353330000 | 2.586655541 |
Table 1: Wide search of the largest ud quark common factors in the proton and within a ± 100 sigma neutron-proton mass ratio.
Table 2 is a refined search listing the series of mass-gluon integer energy combinations that result in the highest common factor peak within the QCD predicted range of ud quark masses. All of these combinations result in a neutron-proton mass ratio within ±3 sigma of the 2010 CODATA value. In all cases, these values create proton ud quark common factor multiples of 360 and 361, and neutron ud quark common factor multiples of 719 and 721. The large common factors between the proton and neutron are themselves a 2 to 1 multiple of each other. This 2X larger common factor in the proton suggests the proton is an inherently more stable particle than the neutron. Figures 5 and 6 provide a graphical view of the quark energy triangles in the proton and neutron using the nominal values from Table 1. The proton and neutron masses can be calculated using Equations (5) and (6) and the nominal values from the Table 2 series:
| Factor | Series Start (n=0) | Series Nominal (n=347) | Series End (n=694) | Series Increment |
|---|---|---|---|---|
| Gluon-Proton (nvp) | 253785286307 | 253785661414 | 253786036521 | 1081 |
| Gluon-Neutron (nvn) | 253431955451 | 253432330211 | 253432704971 | 1080 |
| Up quark mass (nmu) | 612930013 | 612804746 | 612679479 | -361 |
| Down quark mass (nmd) | 1319591725 | 1319467152 | 1319342579 | -359 |
| Largest Factor-Proton | 706661712 | 706662406 | 706663100 | 2 |
| Largest Factor-Neutron | 353330856 | 353331203 | 353331550 | 1 |
| Up Multiple-Proton | 360 | 360 | 360 | 0 |
| Dn Multiple-Proton | 361 | 361 | 361 | 0 |
| Up Multiple-Neutron | 719 | 719 | 719 | 0 |
| Dn Multiple-Neutron | 721 | 721 | 721 | 0 |
| Up quark mass (MeV) | 2.2435666580 | 2.2431081312 | 2.2426496044 | -0.0000013214 |
| Down quark mass (MeV) | 4.8302284660 | 4.8297724795 | 4.8293164930 | -0.0000013140 |
Table 2: Largest common factor series within QCD quark mass predictions for proton and neutron quark bonds within a ± 3 sigma Neutron-Proton Mass Ratio (1.00137841782 - 1.00137842052).
nmp=2×612804746+1319467152+253785661414=256330738058 (9)
nmn=2×1319467152+612804746+253432330211=256684069261 (10)
The large common factor methodology presented in this paper provides a new, alternative method for computing subatomic particle masses and their coupling energies. This method has been applied to the electron-proton model in the search for the exact fine structure constant as well as the proton-neutron model in the search for the updown quark masses. Both models found the largest common factors within the accepted ranges of these constants suggesting this method is valid. The underlying hypothesis that elementary particles share force carrier particles with precise quantities of energy in order to bond using integer multiples of their adjusted Compton wavelengths is a natural extension of what is known and accepted regarding de Broglie wave multiples. Validating this hypothesis would provide another pillar in the Standard Model of particle physics and open the door to new calculations of fundamental particle masses and their coupling constants.