Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2012) Volume 5, Issue 6
For accurate prediction of transmembrane β strands in bacterial porins, we proposed a wavelet support vector machine (WSVM) algorithm to predict the transmembrane β strands in bacterial porins based on the application of WSVM algorithm. The method was applied to all the five porins of known structure (three training proteins, porins from Escherichia coli, Rhodobacter capsulatus and Rhodopseudomonas blastic and two test proteins, porin from Klebsiella pneumoniae and Comamonas acidovorans). For all the five proteins the WSVM method predictived the transmembrane strands in bacterial porins to an average accuracy 84.9%, a higher predictive level than SVM (81.6%) and RNFNN (78.8%) methods. The best test result of the SVM is the precictor with wavelet kernel, which is 84.9% better than other three SVM kernel function of the Gaussian RBF kernel, Polynomial kernel as well as Linear kernel that average 81.6%, 80.3%, and 79.8%, respectively. The experimental results demonstrate the efï¬cacy of the proposed WSVM method.
Keywords: Prediction, Membrane spanning β, strands, Bacterial porin, Wavelet support vector machine, Kernel function
Accurate and reliable prediction of protein structure and function remains a challenge [1]. Of particular importance is the prediction of membrane proteins, as, unlike soluble and fibrous proteins, membrane proteins remain poorly tractable targets for the principal experimental methods of structure determination: X-ray crystallography and multidimensional nuclear magnetic resonance (NMR) spectroscopy [2].
The membrane assembly of outer membrane proteins is more complex than that of transmembrane helical proteins owing to the intervention of many charged and polar residues in the membrane. Accordingly, the predictive accuracy of transmembrane β strands is considerably lower than that of transmembrane α helices [3].
Despite widely different functions, these proteins show a remarkable degree of structural similarity, which has led Schulz to identify 8 rules summarising β-barrel construction [4]. Of these, two are of particular importance when attempting to predict TM β-barrel topology: rule two states that both the N- and C-termini are at the periplasmic end of the barrel, restricting the strand number to even values; and rule 4, that external β-strand connections are long loops (termed L1, L2, etc.), whereas the periplasmic strand connections are generally short (T1, T2, etc.) [2].
Porins are the major component of the outer membrane of Gram negative bacteria. The crystal structures of porins have been studied in atomic detail from three different species namely, Rhodobacter capsulatus [5], Escherichia coli [6], and Rhodopseudomonas blastica [7], Klebsiella pneumoniae and Comamonas acidovorans. They show a common chain fold consisting of 16 anti-parallel β strands of different lengths (6-17 residues) forming a large barrel [3].
A novel type of learning machine called support vector machine (SVM) has been receiving increasing interest in areas ranging from its original application in pattern recognition to other applications such as regression estimation [8-11] due to its remarkable generalization performance. SVM was developed by Vapnik and his coworkers in 1995 [12], and it is based on the structural risk minimization (SRM) principle which seeks to minimize an upper bound of the generalization error consisting of the sum of the training error and a confidence interval [13].
SVM is a new machine learning technology that has been successfully applied in solving problems in the field of bioinformatics. A high-performance method was developed for protein secondary structure prediction based on the dual-layer support vector machine and position-specific scoring matrices (PSSMs). The SVM's performance is usually better than that of traditional machine learning approaches. The performance was further improved by combining PSSM profiles with the SVM analysis [14].
A SVM-based method was developed for predicting families and subfamilies of cytokines using dipeptide composition. The taxonomy of the cytokine superfamily with which the method complies was described in the Cytokine Family cDNA Database (dbCFC) and the dataset used in the study for training and testing was obtained from the dbCFC and Structural Classification of Proteins (SCOP). The method classified cytokines and non-cytokines with an accuracy of 92.5% by 7-fold cross-validation. The method is further able to predict seven major classes of cytokine with an overall accuracy of 94.7% [15].
A support vector machine (SVM)-based method, GPCRpred, has been developed for predicting families and subfamilies of GPCRs from the dipeptide composition of proteins. The method is further able to predict five major classes or families of GPCRs with an overall Matthew's correlation coefficient (MCC) and accuracy of 0.81 and 97.5% respectively [16].
For regression analysis, the non-linear ability of SVM can use kernel mapping to achieve. For the kernel mapping, the kernel function must satisfy the condition of Mercer theorem. The Gauss function is a kind of kernel function which is general used. It shows the good generalization ability. However, for our used kernel functions so far, the SVM cannot approach any curve in L2(Rn) space (quadratic continuous integral space), because the kernel function which is used now is not the complete orthonormal base. This character lead the SVM cannot approach every curve in the L2(Rn) space. Similarly, the regression SVM cannot approach every function [17].
According to the above describing, we need find a new kernel function, and this function can build a set of complete base through horizontal floating and flexing. As we know, this kind of function has already existed, and it is the wavelet functions. Based on wavelet decomposition, this paper propose a kind of allowable support vector's kernel function which is named wavelet kernel function, and we can prove that this kind of kernel function is existent. The Morlet and Mexican wavelet kernel functions are the orthonormal base of L2(Rn) space. Based on the wavelet analysis and conditions of the support vector kernel function, Morlet or Mexican wavelet kernel function for support vector regression machine (SVM) is proposed, which is a kind of approximately orthonormal function. This kernel function can simulate almost any curve in quadratic continuous integral space, thus it enhances the generalization ability of the SVM [17].
In this paper, we develop a wavelet support vector machine (WSVM) algorithm to predict the transmembrane β strands in the family of bacterial porins. A Visual C++ 6.0 program has been developed which takes the amino acid sequence as the input file and gives the predicted transmembrane β strand as output. The proposed WSVM [17] method predicts at an average accuracy level of 84.9% for all the five bacterial porins considered.
If the wavelet function ψ (x) satisfied the conditions: ψ (x)∈L2(IR) , and ψ (x) = 0 , ψ is the Fourier transform of function ψ (x) . The wavelet function group can be defined as
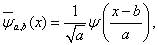 (1)
(1)
where a is the so-called scaling parameter, b is the horizontal floating coefficient, and ψ (x) is called the ''mother wavelet". The parameter of translation b(b∈R) and dilation a ( a > 0 ), may be continuous or discrete. For the function f (x) , f (x)∈L2(R) , The wavelet transform f (x) can be defined as
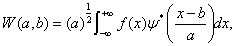 (2)
(2)
where ψ* (x) stands for the complex conjugation of ψ(x).
The wavelet transform W({a,b}) can be considered as functions of translation b with each scale. Eq. (2) indicates the wavelet analysis is a time-frequency analysis, or a time-scaled analysis. Different from the short time Fourier transform (STFT), the wavelet transform can be used for multi-scale analysis of a signal through dilation and translation so it can extract time-frequency features of a signal effectively.
Wavelet transform is also reversible, which provides the possibility to reconstruct the original signal. A classical inversion formula for f (x) is
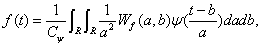 (3)
(3)
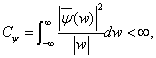 (4)
(4)
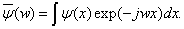 (5)
(5)
For the above Eq. (3), Cψ is a constant with respect to ψ (x) . The theory of wavelet decomposition is to approach the function f (x) by the linear combination of wavelet function group.
Wavelet kernel function
The support vector's kernel function can be described as not only the product of point, such as 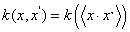 , but also the horizontal floating function, such as k(x, x') = k (x − x' ). In fact, if a function satisfied condition of Mercer, it is the allowable support vector kernel function.
, but also the horizontal floating function, such as k(x, x') = k (x − x' ). In fact, if a function satisfied condition of Mercer, it is the allowable support vector kernel function.
Theorem 1: The symmetry function k(x, x') is the kernel function of SVM if and only if: for all function g ≠ 0 which satisfied the condition of 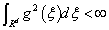 , we need satisfy the condition as follows:
, we need satisfy the condition as follows:
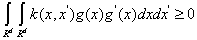 (6)
(6)
This theorem proposed a simple method to build kernel function. For the horizontal floating function, because hardly dividing this function into two same functions, we can give the condition of horizontal floating kernel function.
Theorem 2: The horizontal floating function k(x, x') = k (x − x' ) is allowable support vector's kernel function if and only if the Fourier transform of K(x) need satisfy the condition follows:
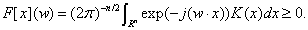 (7)
(7)
If the wavelet function of one dimension is ψ (x) , using tensor theory, the multi-dimension wavelet function can be defined as
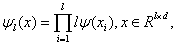 (8)
(8)
where x is a column vector with d dimensions.
We can build the horizontal floating kernel function as follows:
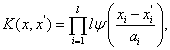 (9)
(9)
where a1 is the scaling parameter of wavelet, a1 > 0. So far, because the wavelet kernel function must satisfy the conditions of Theorem 2, the number of wavelet kernel function which can be showed by existent functions is few. Now, we give an existent wavelet kernel function: Morlet wavelet kernel function. Morlet wavelet function is defined as follows:
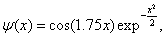 x∈R,w0∈R. (10)
x∈R,w0∈R. (10)
Morlet wavelet kernel function is defined as
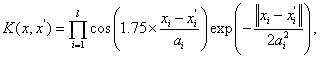 (11)
(11)
where l d , , x R ai R ∈ × ∈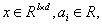 and this kernel function is an allowable support vector kernel function.
and this kernel function is an allowable support vector kernel function.
If we use wavelet kernel function as the support vector's kernel function, the estimation of wavelet support vector machine (WSVM) is defined as
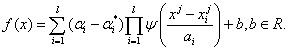 (12)
(12)
For wavelet analysis and theory, see Krantz [18] and Liu and Di [19].
The proposed wavelet support vector machine (WSVM)
In sample set {(xi , yi ),i =1,2,.....,±n} , xi ∈Rn is used as input and yi is used as output. And the ε intensitive loss funcion can be defined as
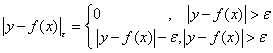 (13)
(13)
The optimal hyper plane of standard support vector machine can be defined as 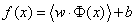
At the same time, combining the wavelet kernel function with support vector machine, we can build a new SVM learning algorithm that is support vector machine on wavelet kernel function (WSVM). The parameter b is taken into account confidence interval of WSVM and form the new variable w of optimal problem, then the new wavelet support vector machine whose e-insensitive tube can be reformulated as
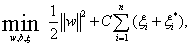 (14)
(14)
Subject to
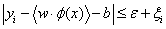 (15)
(15)
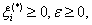 (16)
(16)
where w is a Column vector with d dimensions, C > 0 is a penalty factor, 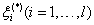 are slack variables.
are slack variables.
Problem (14) is a quadratic programming (QP) problem. By means of the Wolfe principle, wavelet kernel function technique and Karush– Kuhn–Tucker (KKT) conditions, we have the duality problem (16) of the original optimal problem (17)
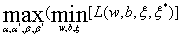 (17)
(17)
and
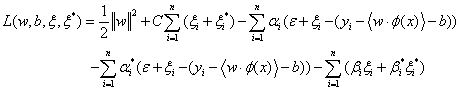 (18)
(18)
The original problem can be transferred to the following problem.
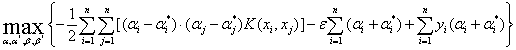 (19)
(19)
Subject to
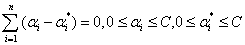 (20)
(20)
According to the KKT condition, we can get the following equation.
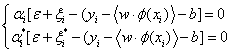 (21)
(21)
Select the appropriate parameters C, and the optimal mother wavelet function which can match well the original series in some scope of scales as the kernel function of WSVM model. Then, WSVM output function is described as following:
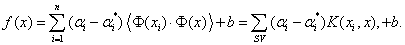 (22)
(22)
Database
The dataset used to derive the statistical models comprises 18 β-barrel membrane proteins of porins found in the Protein Data Bank (Table 1). All proteins share no more than 26% pairwise sequence identity.
| Protein | Organism | PDB ID |
|---|---|---|
| OmpF | Escherichia coli | 1hxx、1hxt、1hxu、1gfo、1gfq |
| OmpC | 2jin | |
| Porin | Rhodobacter capsulatus | 2por、3por |
| Porin | Rhodopseudomonas blastica | 1prn、2prn、3prn、4prn、1bh3、1h6s |
| Ompk36 | Klebsiella pneumoniae | 1osm |
| Omp32 | Comamonas acidovorans | 1e54、2fgq、2fgr |
Table 1: Dataset of 18 β-barrel membrane proteins used for this study.
We applied our predictive method to five different porins from (i) Escherichia coli, (ii) Rhodobacter capsulatus, (iii) Rhodopseudomonas blastica, (iv) Klebsiella pneumoniae, (v) Comamonas acidovorans, for which structures have been determined in atomic detail. We considered the first three proteins (Escherichia coli, Rhodobacter capsulatus and Rhodopseudomonas blastica) as a training set to develop the wavelet support vector machine parameter and the last two (Klebsiella pneumoniae and Comamonas acidovorans ) as a test case.
The accuracy of predicted segments was computed using the equation
Accuracy (%) =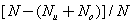
where N, Nu and No are total number of residues, number of residues under-predicted and number of residues over-predicted in a particular protein, respectively [5].
We have predicted the transmembrane β strands for the all five porins and compared our WSVM results with the method of SVM with Gaussian RBF kernel function and RBF neural network (RBFNN). The experimental results are presented in (Table 2). From this table we observe that the WSVM method has the highest predictive accuracy for the protein porin from Rhodopseudomonas blastic (86.8%). Especially the proposed WSVM method predicts the transmembrane β strands of porins from Comamonas acidovorans with higher accuracy (83.4%) than SVM (77.2%) and RBFNN (74.5%) method. By considering all the five proteins, the proposed WSVM method predicts with higher accuracy than SVM and RBFNN methods. The proposed WSVM method predicts the transmembrane β strand for all the five proteins with >83% accuracy and the average accuracy is 84.9%.
| Method | Protein | |||||
|---|---|---|---|---|---|---|
| Escherichia coli | Rhodobacter capsulatus | Rhodopseudomonas blastic | Klebsiella pneumoniae | Comamonas acidovorans | Average | |
| WSVM | 85.2 | 84.6 | 86.8 | 84.7 | 83.4 | 84.9 |
| SVM (RBFkernel) | 84.4 | 82.3 | 82.7 | 81.5 | 77.2 | 81.6 |
| SVM (Polynomial kernel) | 83.2 | 81.4 | 81.3 | 80.1 | 75.5 | 80.3 |
| SVM (Linear kernel) | 82.1 | 80.2 | 80.7 | 79.6 | 76.4 | 79.8 |
| RBFNN | 81.6 | 78.2 | 80.2 | 79.4 | 74.5 | 78.8 |
Table 2: Comparison of predictive ability (%) of three other methods with the present method for bacterial porins.
In our study, wavelet kernel function kernel function is selected as a mapping function. The other popular kernel functions of SVM are:
Gaussian RBF kernel: 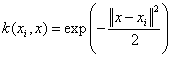
Polynomial kernel: 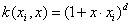
and Linear kernel: 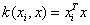
The best test result of the SVM is the predictor with wavelet kernel. The accuracy of SVM with wavelet kernel (84.9%) is better than other three SVM kernel function of the Gaussian RBF kernel, Polynomial kernel as well as Linear kernel that average 81.6%, 80.3%, and 79.8%, respectively. The proposed WSVM method implemented in this study can promote the accuracy of prediction of membrane spanning β strands in bacterial porin.
In this paper, we develop a WSVM algorithm to obtain higher accuracy in transmembrane strand prediction for the family of bacterial porins. The WSVM algorithm algorithm has been automated with a computer program written Visual C++. The proposed WSVM method predicts the membrane spanning β strands with an accuracy of >83% for all the five considered proteins (porins) individually and the average accuracy is 84.9%. These accuracy levels are superior to those of the methods of SVM and RBFNN. The results of application in prediction of membrane spanning β strands in bacterial porin show that the WSVM approach is effective and feasible, the comparison between the SVM method proposed with wavelet kernel function in this paper and other three kernel functions is also given which proves SVM with wavelet kernel function is better than SVM with other kernel functions.