Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2017) Volume 10, Issue 12
It is a recurring limiting factor to obtain sufficient concentrations of soluble proteins using in vitro methodologies. Solubility is an independent characteristic of a protein which can be determined using amino acid compositions under specific experimental conditions. The present study aims at the prediction of protein solubility by adapting machine learning based approaches using the primary structure information. The features involve amino acid compositional features as well as the physiochemical properties of the amino acids i.e. canonical value, hydrophobicity, solubility index and solubility score. For a dataset of 6372 protein sequences (4850 soluble protein sequences and 1522 insoluble protein sequences), all the four features were calculated. Using the calculated values, four different prediction models were developed based on Multilayer Perceptron (MLP), Random Forest (RF), Decision Tree (DT), and Naïve Bayes Classifier (NBC). For performance evaluation, MCC, F-measure, accuracy, precision and recall rate are determined. Among all the four prediction models, MLP has been observed to be the most accurate model for the prediction of protein solubility with an accuracy rate of 95.92%, followed by RF and NBC. The proposed model, based on MLP, can be used for predicting protein solubility as a preprocess of experimental predictions. The method is resource and time efficient, and can help in predicting solubility of proteins instead of laborious and hectic experimental work.
Keywords: Protein solubility; Machine learning; Classification; MLP; D-tree; Naïve bayes classifier; Random forest
Native proteins are always soluble in the host cells when produced in during translation. When these proteins are expressed in Escherichia coli (E. coli) as a recombinant protein, the solubility may alter [1]. Sometimes, the protein is not expressed as a soluble protein and is produced as insoluble inclusion bodies. There are several strategies to refold such inclusion bodies into soluble proteins [2]. One of the strategies is to grow host E. coli cells at very low temperature in order to produce protein slowly [3]. The slow express might help the cell to refold recombinant protein into proper active form. Chaperones, sometimes, helps E. coli to fold the foreign protein into proper refold form. N-terminal detection of the short polypeptide may alter the solubility of the recombinant protein in E. coli [4]. The outer surface of the protein molecule is very important to determine its solubility.
There are two types of amino acids, polar and non-polar. Insoluble proteins, polar residues are exposed to the exterior while non-polar residues, especially hydrophobic residues, are buried in the interior of the protein [5]. These buried non-polar residues confer additional stability to protein. There are many factors which contribute towards solubility recombinant proteins in E. coli. Sometimes, it becomes difficult to get the soluble expression of recombinant proteins in host cells [6]. Even in vitro refolding strategies are unable to fold the protein in active form. In such scenarios, it is important to predict whether a protein would become soluble or insoluble when expressed in the form of recombinant protein in E. coli. Many attempts have been made to predict the solubility of recombinant proteins [7]. There are various parameters which include temperature, pH, charge, protein folding and hydrophobicity [5]. These features have been determined experimentally during the expression of recombinant proteins in E. coli. The sequence and tertiary structure of these proteins play the crucial role in solubilizing protein inside the cell. The present study performs prediction of the solubility based on four classifying models i.e. Multilayer Perceptron (MLP), Random Forest (RF), Decision Tree (DT), and Naïve Bayes classification, along with the performance evaluation.
The methodology was based on four steps, initiating from an input of primary structure of the protein and terminating at the decision, predicting the solubility of that protein (Figure 1).
Dataset
The inputs were taken in the form of amino acid sequences. The dataset was collected from the National Center for Biotechnology Information (NCBI, http://www.ncbi.nlm.nih.gov/) protein database. The query was made using the keyword ‘soluble’ with a SwissProt filter which returned 4850 soluble protein sequences. Another query was made with keyword ‘insoluble’ which returned 1522 sequences. All these 6372 protein sequences were used as dataset for the training and testing of proposed protein solubility prediction model.
Canonical value
The canonical value was determined using the method proposed by Koschorreck et al. [8]. Following equation was used for the calculation of this value.
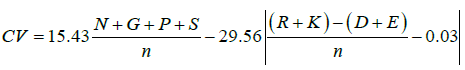
In equation 1, N, G, P and S is the total number of Asparagine, Glycine, Proline and Serine, respectively, in the protein whereas R, K, D and E are the total number of Arginine, Lysine, Aspartic acid and Glutamic acid respectively. Asparagine, Glycine, Proline and Serine are known to form relative turns in the proteins while Arginine, Lysine, Aspartic acid and Glutamic acid represent the total positively and negatively charged amino acids in the protein. The denominator i.e. n represents the total number of amino acid residues in the protein.
Hydrophobicity
The surrounding hydrophobicity of amino acid is represented by the sum of hydrophobic indices of the amino acids which are within the assumed sphere. Therefore, the surrounding hydrophobicity of jth residue in the protein was calculated by assigning the respective hydrophobic indices of jth residue.
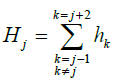
In equation 2, hk represents the hydrophobic index of kth residue, calculated using Kyte and Doolittle [9]. The scale is derived from an amalgam of experimental observations using a moving-window approach which continuously determines the average hydropathy within a defined-size window, moving through the sequence. Using this approach, consecutive scoring is plotted from the N-terminal to the C-terminal. If the hydrophobicity value of amino acid is less than 12.5 than the residue is considered as solvent accessible residue. If the hydrophobicity value is between 12.5 and 13.4 then the residue is considered as partially buried and partially solvent accessible residue. If the hydrophobicity value is greater than 13.4 then the residue is considered as buried.
Solubility index
The solubility index (SI) composition is a mathematic expression used to determine the solubility of protein as proposed by Idicula- Thomas and Balaji [10]. The mathematic expression is as follows:
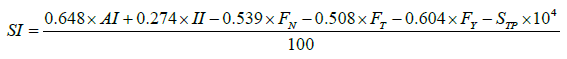
In this parameter, different features were used which are as given below:
• STP = Tripeptide Score
• AI = Aliphatic Index
• II = Instability Index
• FN = frequency of occurrence of Asparagine
• FT = frequency of occurrence of Threonine
• FY= frequency of occurrence of Tyrosine
As the solubility index value depends on the measure of the aliphatic index, instability index and tripeptide score, thus these values need to be computed as well while the frequencies directly refer to count of occurrence. For the calculation of tripeptide score STP , equation 4 is used.
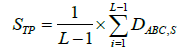
Where L is a total number of proteins while DABC,S is for tripeptide was considered as 0.2. For the calculation aliphatic index (AI), equation 5 learning-based.
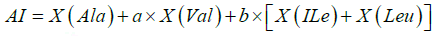
Where X represents a number of residue a=2.9 and b =3.9. Instability index (II) was calculated using equation (6).
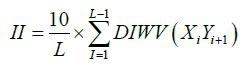
Where L is the number of amino acid residues in the protein and DIWV is the instability weight value for the dipeptide Xi Yi +1, used from the study of Guruprasad et al. [7].
Solubility score
The solubility score was calculated using the Zyggregator method of predicting protein aggregation propensity profiles [11,12]. An initial score was assigned to each residue in the form of a linear combination of specific physicochemical properties, calculated using equation 7.
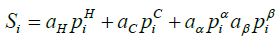
Where 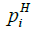 ,
, 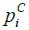 ,
, 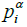 and
and 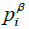 represent the hydrophobicity values from KD scale, charge, α-helix propensity, and the β-strand propensity of residue i, respectively. Moreover, a represents the parameter of the linear combination used from the scale designed by Sormanni et al. [13]. The charge was considered as +1 for positively charged amino acids (Arginine (R) and Lysine (K)) while the negatively charged (Aspartic Acid (D) and Glutamate (E)) were assigned the value of –
represent the hydrophobicity values from KD scale, charge, α-helix propensity, and the β-strand propensity of residue i, respectively. Moreover, a represents the parameter of the linear combination used from the scale designed by Sormanni et al. [13]. The charge was considered as +1 for positively charged amino acids (Arginine (R) and Lysine (K)) while the negatively charged (Aspartic Acid (D) and Glutamate (E)) were assigned the value of –
1. Remaining neutral amino acids were considered with 0 charge value. The α-helix propensity and the β-strand propensity are proposed by Chou and Fasman [14]. From the solubility profile, the solubility score for the whole protein was determined as follows.
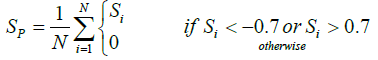
Where N is the length of the protein sequence.
Prediction of protein solubility and performance evaluation
The predictions of protein solubility neighbour on the statistical methods. A model was built to predict the solubility of protein were the amino acid sequence and physiochemical based compositional properties. For the prediction of solubility, four machine learning methods were used. The details of these methods reported in the Table 1.
| Classifier | Classification Approach Used |
|---|---|
| Classifier 1 | Multilayer Perceptron [15] |
| Classifier 2 | Decision Tree [16] |
| Classifier 3 | Random Forest [17] |
| Classifier 4 | Bayes Classifier [18] |
Table 1: Details of Schemes used for prediction of protein solubility.
On the basis of Canonical Values, Hydrophobicity, solubility index and the solubility score, feature set was developed. All the four attributes were considered as individual features and the class label was assigned to each protein. Using these features, four different machine learning classifiers were used for solubility classification of protein.
Firstly, multilayer perceptron was trained to predict the overall solubility of the protein. The network was basically a feed-forward neural network with the backpropagation. The learning rate of the MLP was optimized at 0.3 whereas the momentum rate for backpropagation was set as 0.2. Moreover, a number of epochs were considered as 500 while the threshold for a number of consecutive errors was set as 20. Seeding and percentage of validation set were set as 0, considered default for MLP. Decision Tree, Random Forest and Naïve Baise classifiers were also used for the prediction of protein solubility. A total of 100 iterations were considered for all these approaches. For the Random forest, bagging size was considered as 100.
Through the supervised learning approaches, four models were implemented and the evaluation of these models was based on some statistical approaches. The prediction performance of all the four models was evaluated by dividing the results into four major categories i.e. true positive (TP), true negative (TN), false positive (FP), and false negative (FN). Here TP and TN represent the correctly classified soluble and insoluble protein instances, respectively whereas FP and FN represent the incorrectly classified soluble and insoluble protein instances, respectively. Using these four categories of results, the binary predictions of results were assessed on the basis of different criteria. Accuracy, precision, recall, F-score and Mathew’s correlation coefficient (MCC) were used for evaluation of prediction performance. Accuracy is actually the proportion of the correctly identified instances overall instance whereas precision and recall are based on the correctly identified soluble proteins only. F-score is the harmonic mean of the precision and the recall while the MCC is correlational matrix technique which aids in the adjustment of unbalance results. The statistical evaluation was carried out using equation 9-13.
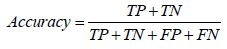
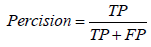
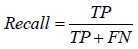
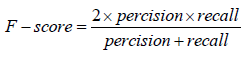
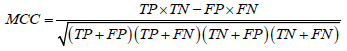
Considering further evaluation, ROC curve was also plotted and are under the curve represented the correctness of models.
Sequence and composition based calculations
The canonical value being observed was different for both types of proteins, soluble and insoluble. The value for soluble proteins was observed to be within the range of 0.7 to 1.65 while the insoluble proteins had values of greater than 1.7. While training the MLP, it was observed that the finalized value of the threshold for the canonical value was 1.706, usually considered as 1.71. Above this value, the proteins were predicted to be insoluble. It was observed that the sequences having more negatively charged residues have increases predicted solubility as compared to that sequence which has positively charged residues. On the basis of solvent accessibility of the residues, the overall hydrophobicity of the protein was calculated. It was observed that for insoluble proteins, the value of hydrophobicity was above 75% while the soluble proteins showed higher value of hydrophilic residues. The solubility index was calculated on the basis of the STP , AI, II and the frequencies of Asparagine, Threonine and Tyrosine. It was observed that the solubility index for soluble proteins was more than or equal to 1 while for insoluble proteins, it was less than 1. On the basis of Zyggregator method, the solubility score was observed to be ranging in 0 to 1 for soluble proteins while it was observed 0 to -1 for insoluble proteins.
Prediction of solubility and performance evaluation
Out of 6372 instances of the proteins, data was divided by the ratio of 70% (n=4460) for training and 30% (n=1912) for testing. For all the 4 classifiers, used for the prediction of solubility, performance and accuracy metrics were computed which are provided in Table 2. MLP was observed to be predicting protein solubility with the highest accuracy among all the 4 classifiers used. The evaluation was made on the basis of the four classes of results i.e. (TP, TN, FP and FN) and ROC area.
| Summary | Multilayer perceptron results | Decision Tree results | Random Forest results | Naïve Bayes classifier results |
|---|---|---|---|---|
| Total Instances for testing | 1912 | 1912 | 1912 | 1912 |
| Correctly classified instances | 95.9205% (n=1834) | 92.7301% (n=1773) | 95.8682% (n=1833) | 95.8912% (n=1833) |
| Incorrectly classified instances | 4.0795% (n=78) | 7.2699% (n=139) | 4.1318% (n=79) | 4.0795% (n=79) |
| True Positive | 1379 | 1312 | 1377 | 1378 |
| False Positive | 78 | 72 | 77 | 77 |
| True Negative | 455 | 461 | 456 | 456 |
| False Negative | 0 | 67 | 2 | 1 |
| True Positive Rate | 0.959 | 0.927 | 0.959 | 0.959 |
| False Positive Rate | 0.106 | 0.111 | 0.105 | 0.104 |
| Precision | 0.961 | 0.927 | 0.961 | 0.961 |
| Recall | 0.959 | 0.927 | 0.959 | 0.959 |
| F-Measure | 0.958 | 0.927 | 0.958 | 0.958 |
| MCC | 0.899 | 0.819 | 0.897 | 0.899 |
| ROC Area | 0.922 | 0.908 | 0.921 | 0.928 |
| PRC Area | 0.935 | 0.897 | 0.935 | 0.933 |
Table 2: Computed accuracy and performance evaluation.
Various models have been proposed in different studies for predicting the protein solubility. Moreover, the approaches being used in each method are different. A thorough comparison is made on the basis of accuracies being reported and the features used. (Table 3) illustrates the comparison. Diaz et al. used molecular weight, Cysteine fraction, hydrophobicity-related parameters, approximate charge average and fractions of amino acids. The dataset for this study contained 212 protein sequences and the accuracy being reported was 93.9% [19]. Another method was proposed by Samak et al. in which dataset contained almost 1600 protein sequences and the features reported were 39 in the count. SVM and Random forest were used for prediction model and highest accuracy reported was 90% using SVM [20]. Xiaohui et al. also used the SVM as predictor model and the dataset contained almost 6000 protein sequences. The accuracy reported was 88% [21]. Huang et al. reported 84% accuracy using the SVM while the feature used was dipeptide composition only. There were four datasets used for the model training and testing, having various numbers of soluble and insoluble protein sequences [22]. Fang and Fang, 2013 presented a model based on random forest classification while they reported the accuracy of 83%. Features reported were 17 in count while the dataset had 1918 protein sequences [23].
| # | Method | Accuracy | Area under curve | F-score | Mathew correlation coefficient | Precision | Recall |
|---|---|---|---|---|---|---|---|
| 1 | Proposed Methodology | 0.96 | 0.922 | 0.96 | 0.9 | 0.96 | 0.96 |
| 2 | Diaz et al., 2010 | 0.94 | - | - | - | - | - |
| 3 | Samak et al., 2012 | 0.90 | - | - | - | - | - |
| 4 | Xiaohui et al., 2014 | 0.88 | - | - | 0.76 | - | - |
| 5 | Wilkinson and Harrison,1991 | 0.88 | - | - | - | - | - |
| 6 | Fang and Fang, 2013 | 0.84 | 0.91 | - | 0.67 | - | - |
| 7 | Huang et al., 2012 | 0.84 | - | - | - | - | - |
| 8 | Chan et al., 2010 | 0.83 | 0.89 | 0.75 | - | 0.73 | 0.78 |
| 9 | Niwa et al., 2009 | 0.8 | - | - | - | - | - |
| 10 | Kumar et al., 2007 | 0.79 | 0.76 | - | - | - | - |
| 11 | Goh et al., 2004 | 0.76 | - | - | - | - | - |
| 12 | Smialowski et al., 2012 | 0.75 | - | - | 0.39 | 0.65 | 0.76 |
| 13 | Stiglic et al., 2012 | 0.75 | 0.81 | - | - | - | - |
| 14 | Magnan et al., 2009 | 0.74 | 0.74 | - | 0.49 | 0.74 | 0.74 |
| 15 | Idicula-Thomas et al., 2006 | 0.74 | - | - | - | - | - |
| 16 | Smialowski et al., 2007 | 0.72 | 0.78 | - | 0.43 | - | 0.72 |
| 17 | Idicula-Thomas et al., 2005 | 0.72 | - | - | - | - | - |
| 18 | Hirose et al., 2011 | 0.71 | - | - | - | 0.85 | 0.74 |
| 19 | Hirose and Noguchi, 2013 | 0.68 | 0.78 | 0.67 | 0.42 | 0.56 | 0.85 |
| 20 | Christendat et al., 2000 | 0.65 | - | - | - | - | - |
| 21 | Bertone et al., 2001 | 0.63 | - | - | - | - | - |
Table 3: Comparison with previously reported studies (sorted on accuracy).
Wilkinson and Harrison presented a regression-based model with an accuracy of 88% while the features being used were based on amino acid correlations. A total of 81 protein sequences were used for model training and testing [24]. Chan et al. used SVM for solubility prediction. Feature set was comprised of 617 features based on recombinant fusion proteins while the 3 different combination models were trained. Highest accuracy was observed to be 83% [25]. Another SVM based approach was reported by Niwa et al. The features being used for this model were molecular weight, isoelectric point (pI) and ratios of each amino acid content. The dataset was comprised of 4312 proteins while the accuracy reported was 80% [26]. The work proposed by Kumar et al., 2007 used an extended approach of SVM as in Granular Support vector machines (GSVM). The model used 27 features with almost 200 proteins sequences. The final accuracy being reported was 79% [27].
Goh et al. worked on a different mechanism for prediction i.e. Decision tree while the random forest method was used for feature selection. The dataset contained 27267 protein sequences and the features used were 5. Results were reported to be 76% accurate [28]. Smialowski et al. reported a model based on two-layered architecture with wrapper method for feature selection while used almost 82000 protein sequences. The accuracy reported was 75%. The results were observed to be more accurate than a previously reported study in 2007, based on a two-level structure comprising of SVM and Bayes classifier [29]. Other decision tree based approach were reported by Christendat et al. and Bertone et al. were 65% and 63% accurate, respectively [30,31].
Stiglic et al., used 21 features in the count while the dataset contained 1625 proteins. Accuracy being observed was 75% [32]. Mangan et al. also reported the SVM based protein solubility prediction mode with an accuracy of 74%. The feature set was observed to be consisting of 23 feature groups while dataset was comprised of 17408 proteins [33]. Idicula-Thomas et al. used a heuristic approach for computing protein solubility using Tripeptide score, aliphatic index, instability index of the N terminus and frequency of occurrence of the amino acids Asn, Thr, and Ty. Dataset was comprised of four groups while the accuracy reported was 72% [10]. Moreover, an extension of work was also reported in 2006, on the basis of SVM, KNN and linear logistic regression and the accuracy observed was 76% [34].
Hirose et al. reported the overexpression and the solubility of human full-length cDNA in E. coli and structural features on protein expression/solubility in each system was evaluated and a minimal set of features associated with them was estimated. The datasets being used were 2 different while features extracted were 437. Model was based on random forest and the results were observed to be 71% accurate [35]. The extension in this work, reported in 2013, using SVM, random forest and nearest neighbor method was only 68% accurate [36].
The extent of protein’s solubility can indicate the quality of its function. Over 30% of synthesized proteins are not soluble. In certain experimental circumstances, including temperature, expression host, etc., protein solubility is a feature eventually defined by its sequence. Until now, numerous methods based on machine learning are proposed to predict the solubility of protein merely from its amino acid sequence. In this study, a computational approach is presented for estimating the possibility of protein solubility from the primary structure of the protein, on the basis of the amino acid compositional features as well as the physiochemical properties of the amino acids. The feature set comprises of canonical value, hydrophobicity, solubility index and solubility score. This study aimed to investigate extensively the machine learning based methods to predict recombinant protein solubility, so as to offer a general as well as a detailed understanding of protein solubility and its relation with primary structure of the protein. MLP was observed to be predicting protein solubility with the highest accuracy among all the 4 classifiers used. The evaluation was made on the basis of the four classes of results i.e. (TP, TN, FP and FN) and ROC area. Among all the four classifiers, MLP has been observed to be the most accurate model for prediction of protein solubility with an accuracy of 95.92%. The computational approach, proposed in this study is observed to be the most accurate in terms of throughput as compared to the methods presented by various researchers, till now.