Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2015) Volume 8, Issue 1
Platinum compounds are very important to treatment of various malignant tumors. However, prediction of platinum-binding sites is very hard to be made. Nevertheless, hydrolysis of leaving groups bounded to platinum compounds plays an important role in delivering platinum to a target molecule. Herein, a study in silico provides an understanding of the molecular surface in atomic level of three-dimensional structure of cisplatin and transplatin and their binding-sites in order to offer some insights in drug designing. The goal of this work was to implement a new approach based on geometric and physicochemical parameters to find platinum-binding sites using parallel computing algorithms for graphics processing units (GPUs). These algorithms were tested and validated by analysing platinum-binding sites in five known proteins. The results indicated that these binding sites were predicted with significant success. In our analysis HexServer and PatchDock server did not find putative binding-sites for cisplatin and transplatin as we found for the five chosen proteins. Herein, we have shown that the present method have had a better prediction of platinum-binding site than HexServer and PatchDock methods.
Keywords: Binding sites, Hydrogen bonds, Cisplatin, Transplatin, Molecular surface, GPU computing
3D: Three-Dimensional; GPUs: Graphics Processing Units; CUDA: Compute Unified Device Architecture; CPU: Central Processing Unit; PDB: Protein Databank; FFT: Fast Fourier Transform
Three-dimensional structures (3D) of proteins and ligands reveal a significant geometrical correspondence between their contact regions [1], i.e., shape complementarity and other physicochemical characteristics of protein surfaces determine the nature of interaction between the protein’s binding-site and the ligand [2]. It is reasonable that analysis of protein’s binding-sites are crucial in order to provide a better understanding of their structure and function, which are important parameters to drug discovery field. As binding-sites contains amino acid residues involved in interactions that require a well-defined arrangement [2], a challenge is to identify groups of interaction between protein and its ligand. Furthermore, bindingsites might be influenced by environment properties, such as pH, ionic strength and high ordering of water molecules [3]. Hence, the process of binding-site analysis relies on identifying atoms likely to establish hydrogen bond, which plays a fundamental role in protein ligand interaction [4] and is pointed as a driven force to the higher degree of selectivity between protein and ligand [4]. For this reason, analysis of binding-site takes into account the atom type and its relative position to neighbouring atoms [5]. In addition, molecular surface characterization at atomic level of platinum compounds affords an opportunity for the development of novel and better drugs. For instance, cisplatin and transplatin are widely used anticancer drugs. They are suitable for many types of cancer, such as testicular, ovarian, cervical, colorectal and relapsed lymphoma cancer [6,7]. Interestingly, the trans isomer of cisplatin known as transplatin is less cytotoxic [8], which is argued as a consequence of steric mechanisms that influence the way transplatin interacts with its target molecules [9]. Generally, methods employed to identify protein binding sites use static 3D protein structures to compute their geometry or energy. Examples of methods that use geometric parameters of protein shape are: CAST [10], PASS [11], PocketPicker [12], and Fpocket [13]. On the other hand, methods that compute the energy simply use van der Waals forces to describe protein shape, i.e., Q-SiteFinder [14]. There are methods that use grid algorithm to compute the energy of an interaction as the sum of Lennard-Jones potential, coulombic attractions and directional hydrogen bond energy terms [15,16]. For instance, Cavbase [17] combine structure and sequence comparison in its analysis process by describing and comparing protein binding pockets on the basis of their geometrical and physicochemical properties. On the other side, to analyse a binding-site, a set of representative conformations of proteins can be obtained from classic molecular dynamics simulations [18-20]. However, static analysis is not always enough to understand the mechanisms of interaction of binding-sites and a representative example of this lack of understanding is cytokine IL-2 [21,22]. Actually, recent advances in parallel computation based on GPUs have improved the computational resources available, allowing GPUs to be used as performance accelerators for a wide variety of scientific applications [23]. In this article, we propose a new approach based on geometric and physicochemical properties to find binding-sites using parallel computing algorithms for GPUs. Herein, cisplatin and transplatin were the chosen ligands for this study in order to analyse how hydrogen bonds drive interactions between protein and ligand. The proposed approach consists in analysing the exposed surface area of each atom of proteins and ligands, as well as its relationship with the point of highest electrical potential on molecular surface. Therefore, to rank the best candidates for binding sites, an empirical scoring function was created. It was made by selecting atoms of highest electrical potential on exposed surface area and adding terms such as lipophilicity [24], which represents the hydrophobic effect [25-27], and geodesic distance between points of highest electrical potential on surface, which exemplifies the geometric complementarity between protein and ligand. A geodesic is a locally length-minimizing curve used for shape analysis, surface evolution and object recognition [28]. This analysis at the atomic level aims to offer new insights towards the understanding of the effectiveness of each atom in establishing hydrogen bonds on molecular surface and inspire development of novel methods to analyse small ligands.
Preparation of ligands structures
Cisplatin and transplatin structures were modeled through GaussView/Gaussian09 [29]. These structures were optimized using MPW1MPW91 [30] method with SDD (Stuttgart/Dresden) [31] basis function. Partial charges were calculated using the QTPIE method [32] implemented by using C++ Open Babel library [33]. Cisplatin and transplatin structures are provided in the supplementary information.
Preparation of protein structures
The proteins were selected for the study based on the protein databank [34]. To make sure about the validation of our method we have chosen five proteins that had binding-sites well determined through experimental data and a description of which residues of each binding-site interact with cisplatin and transplatin. For instance, cuprozinc superoxide dismutase (PDB ID: 2AEO) was selected because its crystallization with cisplatin shows an interaction of platinum with His 19 [35], which can be visualized through electron-density map. For chaperone-monomer (PDB ID: 3IWL) the residues Cys 12 and Cys 15 [36] bind platinum, which also can be seen through electron-density map. In the case of myoglobin (PDB ID: 1MBN) the platinum bindingsite was found through mass spectrometry technique, and His 116 and His 119 [37] were determined as the residues that bind cisplatin and transplatin. In addition, ubiquitin (PDB ID: IUBQ) had also the platinum binding-sites determined by mass spectrometry. Ubiquitin has two binding-sites in which the residue for the first binding-site is Met 1 and the second is His 68 [38]. Finally, the protein BCL-2 (PDB ID: 1G5M) was chosen because its structure was determined by NMR technique and there was a precise description about the residue that binds to platinum, which is Glu 13 [39]. In this work, all selected proteins have no covalently bound HETATM but only coordinated groups such as cofactors (Cu, Zn or Heme group) or water. In addition, we have added hydrogens in proteins whose PDB were missing hydrogens. That was done by using HADD software [40] and partial charges of all atoms within the proteins were calculated by the same method used to ligand structures.
Mapping molecular surfaces
A software named MSProt based on C++ was developed by using the open source framework Qt version 5.3.2 (http://qt-project. org) with OpenGL (http://opengl.org) in order to map and view molecular surfaces in 3D environment structure. A parallel computing platform called CUDA [41] was used to speed up numerical linear algebra operations. Therefore, to map molecular surface area the skin surface method [42] was used, which was implemented through C++ Computational Geometry Algorithms Library (CGAL), library (http://cgal.org). Kuhn, Schmitt and Klebe have employed a method in which they used vectors to define a set of properties that guide molecular recognition: hydrogen bond acceptor and hydrogen bond donor [17]. Adjustments that were made on Kuhn, Schmitt and Klebe’s method is shown in Figure 1. Details about how every vector v was calculated for amino acids and ligands were summarized in the supplementary information. The exposed surface area was calculated by using algorithm 1. Hence, instead of use vector r as proposed by Kuhn, Schmitt and Klebe’s method, a vector p was calculated by taking the point of maximum electric potential on the molecular surface of the region of sphere 3. Further information about this adjustment is provided in Figure 1. To calculate the electric potential at each triangle belonging to the mesh formed by skin surface in sphere 3, the algorithm 2 was used. The sphere 3 represents the region of molecular surface to be coloured according acceptor and donor properties. The function kernelPotenc (explained later on) fixes the exposed area, which can vary between 0-10 Å2 (see Figure 6), according to the values of electrical potential calculated through the partial charges. Therefore, the size of the colored area is determined by the electrostatic potential, and the colored area cannot exceed the maximum radius of 2 Å determined by sphere 3 as defined by Kuhn, Schmitt and Klebe’s method. Figure 2 shows an example of mapping of myoglobin. Figure 3 shows an example of mapping of cisplatin.
Figure 1: Adjustments made on Kuhn, Schmitt and Klebe’s method. For both A and B: 1 - Represents the van der Waals surface. 2 - Represents the molecular surface (skin surface). The sphere 3 represents the local map. Two vectors, v and p, define the exposure of a particular physicochemical property. The standard vector v represents the mean direction of the physicochemical property exposure, herein the acceptor property. Instead of use vector r as a normalized summation of all vectors pointing to the surface grid, vector p was used. The vector p is defined by the point of greatest electrostatic potential on the skin surface inside the sphere 3 region. Cut-off values to β angle between v and p were the same used by Kuhn, Schmitt and Klebe’s method for the vectors v and r. For instance, in A the molecular surface approximates to the van der Waals surface and the value of β is small, while in B the molecular surface moves away from the van der Waals surface and the value of β is large. Therefore, it was considered that the larger the exposed area and the smaller the β angle, the better to atoms establish hydrogen bonds. The acceptor vary from 0 to 10 A2.
The geodesic of ligands
Permutation is defined by analytic combinatorics as an ordered sequence without repetition, this concept was used to list a minimum of two points and a maximum of six points as possible sequences, these limits is due to the number of hydrogen bonds that cisplatin and transplatin can establish. Hence, by taking labelled points on ligand surface, sequences from two to six points were made as shown in figure 3. The length of each sequence of points was calculated by geodesic algorithm [43], and the lowest length was stored for further analysis of the distances between the ligand and protein. This was done for each sequence of points generated by permutation.
The geodesic of protein
The same process of permutation described as before was conducted to the points of the protein molecular surface. In order to calculate the shortest path among these points, a virtual sphere was used to select the points that falls within. That virtual sphere represents the ligand (cisplatin or transplatin) whose measured distance between two internal atoms in the optimized ligand structure was measured as 4.94 Å, which was considered to be the diameter. Hence, the used virtual sphere had a radius of 5 Å whose diameter of 10 Å was assumed to be the double of 4.94 Å, i.e., the size of the virtual sphere was enough to roughly mimic the ligands. The points’ selection was made by positioning the center of the virtual sphere at the first referential point of maximum electric potential, and all points that dropped within the sphere were collected according figure 4. Thus, it was repeated to each labelled location of maximum electric potential of the protein. The same process of permutation created several sequences, which had not exceeded the maximum number of six elements for the reason described in geodesic of ligands.
Ranking of binding sites
The ranking analysis was speeded up by discarding sequences through the employment of four parameters. The first parameter is the geodesic value among points of greatest electrostatic potential between the protein and the ligand. For protein analysis in relation to a chosen ligand, the difference between the paths formed by the geodesic distances was established as 0.4 Å. The second parameter was the perimeter, which was obtained for both the protein and the ligand as the sum of the measured distances of acceptor and donor atoms, respectively. Hence, the difference between the sum of distances among the acceptor atoms of the protein and the sum of distances among the donor atoms of the ligand were calculated and assigned to be lower than 0.2 Å. The third parameter considered was the alignment of these structures. The points of greatest potential were aligned and the rootmean- square deviation (RMSD) [44] was calculated (Figure 5). Herein, the range of 1.1 < RMSD <2.6 was considered satisfactory, whether to determine if the ligand have not superimposed over the protein or if it is in a far region of the binding site. The last parameter was the total acceptor area of the protein and the total donor area of the ligand. In order to calculate the total acceptor area it was summed up the exposed area of each acceptor atom from the sequence that was established by permutation. The same was done to each donor atom of the ligand. Thus, the difference between the total acceptor area and total donor area was determined as being lower than 0.4 Å2. These parameters are shown in figure 5. Figure 6 shows the relationship between the acceptor exposed area and the angle formed between vectors v and p. The present study has considered only the protein’s acceptor atoms and the ligand’s donor atoms to search for binding-sites. Thus, the scoring function was developed based on the relation between acceptor and donor groups found in proteins and ligands respectively. Herein, the goal was to minimize the score function, where the lower the value of the score function the easiest to establish a hydrogen bond, which was in agreement to figure 1. Hence, for ranking of binding-sites it was assumed the following terms to the scoring function:
SF=P+ST (1)
The term P represents the effectiveness of each atom in the hydrogen bond on molecular surface.
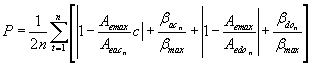 (2)
(2)
Aemax corresponds to the maximum exposed area of each atom whose value is 10 Å2. This value was obtained by our measurements of all exposed areas of the atoms studied (Figure 6). Aeac is the exposed area corresponding to the acceptor atom that interacts with the donor atom whose exposed area is represented by the term Aedo. βmax is the maximum angle between the vectors v and p, which has the value of 100º that was extracted from Kuhn, Schmitt and Klebe’s method. Finally, the sum has n>1 where n corresponds to the number of hydrogen bonds. The c term was prepared to assign a quantitative analysis for the type of each amino acid to be analyzed in relation to its hydrophobicity. This term consists:
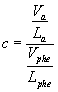 (3)
(3)
Va is the volume of amino acid divided by its lipophilicity (La). La values were extracted from table 2 of El Tayar scale [24] of experimental measurements, as well as volume values were obtained from table 1 [24]. Hence, Vphe and Lphe stand by volume and lipophilicity of phenylalanine, which was chosen as the parameter of comparison. According to Monera [45], phenylalanine is the most hydrophobic amino acid at pH 7.
| PDB ID | Number of triangles | Time (s) |
|---|---|---|
| 1G5M | 10466944 | 1457.64 |
| 1MBN | 9422144 | 1130.57 |
| 2AEO | 15059136 | 3598.5 |
| 1UBQ | 4667712 | 353.12 |
| 3IWL | 3426496 | 227.54 |
Table 1: Number of triangles of the triangular mesh and execution time for the algorithms on GPUs.
| PDB ID | Rank 1 | Rank 2 |
|---|---|---|
| 1G5M | 2 | * |
| 1MBN | 1 | 5 |
| 2AEO | 3 | * |
| 1UBQ | 2 | 1 |
| 3IWL | 1 | * |
*Data not found in the literature about the binding sites of these proteins with transplatin.
Table 2: Ranking for each site found. Rank 1-position of the binding site found in relation to the ten best ten candidates for cisplatin. Rank 2-position of the binding site found in relation to the ten best candidates for transplatin.
The term S describes the quality of fitting:
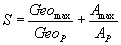 (4)
(4)
GeoP represents the geodesic of protein. AP is the total acceptor area of protein. Herein, the value of 8 Å for Geomaxwas the maximum allowed by fitting the ligand. As the total number of allowed hydrogen bonds is six, Amax assumes the value of 60 Å. That total number of allowed hydrogen bonds corresponds to possible hydrogen bonds of cisplatin or transplatin.
The term T represents the fit between the protein and the ligand. Ideally, this term is equal to 1, which indicates a good fit.
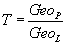 (5)
(5)
GeoLig is the geodesic of ligand.
Algorithms for GPUs
In CUDA’s architecture, Device is the given name to GPUs and Host is the CPU, further information is provided by CUDA C Programming Guide (http://www.nvidia.com). To make a good use of all hardware capabilities provided by GPUs an appropriate number of threads is selected per block, and an efficient access to global memory is ran. CUDA’s architecture is based on the implementation of extended functions of C language called kernels. These functions are executed n times in parallel by n different threads. Herein, the source code of the kernel functions’ implementation is provided in the supplementary information to show how they work. Two algorithms were employed to analyse biomolecules, the first one was labelled as kernelExposeArea as well as the second as kernelPotenc. The first algorithm was employed to calculate the exposed area of each atom that represents a physicochemical property, and the second algorithm was applied to calculate the electric potential of each triangle on the molecular surface by taking into account each atom that belongs to the protein’s structure and its partial charge.
Steps of the algorithm 1 in kernelExposeArea
1 - Memory allocation of points from the center of the atom and the vector points v. These data will be shared by each thread of the same block.
2 - Synchronize threads before continuing execution.
3 - Calculate the midpoint representing the center of the triangle, which will be the vector b. The vector b is only an auxiliary vector for calculating the area of the exposed property.
4 - Check if the triangle is inside the sphere 3 (Figure 1) through the vector b module. That sphere has a radius of 2 Å, which can be subsequently influenced by the electric potential as described in the mapping of molecular surfaces.
5 - If the vector b is within the sphere then calculate the angle between v and b.
6 - If the angle is less than or equal to 100º, the triangle’s vertices are stored in global memory and sent to the Host.
In Host with these selected vertices, the exposed area was calculated. These selected vertices were sent to Device and ran in the kernelPotenc. Figure 7 shows how the kernelExposeArea was implemented regarding the threads and memory access.
Steps of the algorithm 2 in kernelPotenc
1 - Calculate the midpoint representing the center of a triangle.
2 - Calculate the vector between the triangle’s midpoint and the atom’s centre.
3 - Calculate the magnitude of the vector r.
4 - Read in global memory each atom position and partial charges.
5 - Calculate the electric potential at the midpoint of the triangle by vector r.
6 - Store the electrical potential of the triangle in the global memory to be sent to Host.
The kernelPotenc is performed for all triangles that fall inside of the sphere 3 (Figure 1), and along this calculation the maximum value to form the vector p is extracted. Figure 8 shows how the kernelPotenc was implemented regarding the threads and memory access. In implementing this work, a computer with 32 GB DDR 3, a core i7 processor 3.40 GHz and a video card Titan Black from Nvidia with 2880 CUDA cores and 6144 MB memory was used.
Compare results with other methods
In order to compare our method to existing methods we have chosen HexServer [46] and PatchDock [47] to run an analysis in which the binding-sites of cisplatin and transplatin were investigated. Protein docking algorithms, such as HexServer and PatchDock, usually assume that the proteins are rigid, though proteins are intrinsically flexible. These algorithms use geometric hashing [48] or fast Fourier transform (FFT) correlation techniques [49] in order to find a reduced number of putative docking orientations that could be enhanced using other techniques. HexServer is a FFT-based protein docking server based in GPUs and PatchDock is based on a rigid-body geometric hashing algorithm. Thus, we ran HexServer and PatchDock using their default conditions and in our analysis and we have compared our method with the ten first results of HexServer and PatchDock.
Figure 9 shows the total execution time of kernels. By viewing Figure 9, we note that the kernels execute much faster on GPUs. The number of triangles processed by kernels is shown in Table 1. Given that the binding-sites were found, deletion of HETATM has had no influence over the determining of the platinum binding-sites of the chosen proteins. For instance, the PDB of chaperone-monomer (PDB ID: 3IWL) has as HETATM two sulfates, a TCEP ligand (3,3',3''-phosphanetriyltripropanoic acid) and water molecules, and all these HETATM are not covalently bound to chaperone-monomer. For myoglobin (PDB ID: 1MBN) there were water molecules and one heme group, which were not covalently bound to myoglobin and do not interfered in finding the platinum binding-site. On the other hand, cuprozinc superoxide dismutase (PDB ID: 2AEO) has metallic cofactors (two of each: Zn and Cu) and water molecules as HETATM. They were removed without disturbing the location of platinum binding-site. Ubiquitin (PDB ID: 1UBQ) had only water molecules as HETATM and their deletion did not bring any concerns to our proposed work. Lastly, BCL-2 (PDB ID 1G5M) had no HETATM on its PDB. We could determine if a found binding-site was a false positive by comparing our results with the literature. If a found binding-site was not the same as described by the literature or close enough to the known binding-site, we took our result as a false positive (see supplementary information). Table 2 summarizes the best candidates for the binding-site of the initial process of molecular recognition. For instance, the first analysed protein was superoxide dismutase cuprozinc, which has a platinumbinding site located at His 19 [35]. Herein, the platinum-binding site containing this amino acid was ranked in the third place. Therefore, the ranked binding-site was taken as valid. On the other hand, ubiquitin has a platinum-binding site on Met 1 and His 68 [38]. The bindingsite His 68 was ranked in second place. However, Met 1 binding-site was not found, which could be interfered by the lack of hydrogens at the beginning of the analysed protein. The developed method has not considered adding or removing hydrogens in the protein structure in order to mimic the pH in vivo, which certainly influence the surface potential. The next analysed protein was myoglobin [37]. Myoglobin has a site located exactly between His 116 and His 119, which were accurately found by the present method in first place. The penultimate protein analysed was chaperone-monomer, which the platinumbinding sites are Cys 12 and Cys 15 [36]. Herein, our method found Cys 15 and Lys 60 as platinum-binding sites of chaperone-monomer. As these binding sites were extremely close to Cys 12 and Cys 15 and they were ranked in first place, it was suggested that the binding-site is valid. For BCL-2 protein the analysis were more complicated, because the structure of this protein was defined by NMR technique that provides several models, and only the first model was analysed. According to article [39] there are some potential binding sites for cisplatin such as Glu 13. Indeed, in our method Glu 13 was ranked in second place. Once binding-site for cisplatin was investigated we started to seek for transplatin binding-sites. By analysing how transplatin binds to ubiquitin [38] it was seen that transplatin binds at the same region that cisplatin binds in ubiquitin. In addition, for myoglobin the transplatin binding-site His 116 was found, as it was expected according to the literature [37]. As the literature shows that cisplatin and transplatin binds similarly to myoglobin, it was considered that the present method pointed the binding site to transplatin in a very satisfactory way. Table 3 represents binding sites found for cisplatin and table 4 demonstrates the binding sites to transplatin. Finally, we ran HexServer and PatchDock to compare with MSProt. Intriguingly, HexServer did not find putative binding-sites for cisplatin and transplatin as we found for the chosen proteins. In addition, PatchDock only found Glu 13 in the first place of PatchDock’s ranking as the residue that binds just cisplatin for 1G5M, but not to any other residues for the remaining proteins. Further information of our analysis can be found at the supplementary information.
| PDB ID | Binding sites | Acceptor atoms | Donated atoms |
|---|---|---|---|
| 1G5M | Met 16 | SD | H5 |
| Glu 13 | OE1 | H2 | |
| 1MBN | His 116 | O | H1 |
| His 119 | O | H3 | |
| Pro 120 | O | H4 | |
| 1UBQ | Ile 44 | O | H3 |
| His 68 | NE2 | H1 | |
| 2AEO | Thr 30 | OG1 | H6 |
| His 19 | NE2 | H3 | |
| 3IWL | Lys 60 | NZ | H3 |
| Cys 15 | SG | H4 |
Table 3: All binding sites for cisplatin.
| PDB ID | Binding sites | Acceptor atoms | Donated atoms |
|---|---|---|---|
| 1UBQ | Ile 44 | O | H6 |
| His 68 | NE2 | H4 | |
| 1MBN | His 116 | NE2 | H6 |
| Gln 128 | NE2 | H1 |
Table 4: All binding sites for transplatin.
In our method we first decide which atoms are important to calculate the vector v, which is used to limit the acceptor and donor areas of each residue. As MSProt is still in development, in future work our method will take into account all hydrogen bonds and interaction forces that hold cofactors seen as HETATM, and we are going to use that approach to increase the range of proteins that could be submitted to our method. Herein, we showed the applicability of algorithms to predicting binding-sites of cisplatin and transplatin compounds. As a perspective of future, an analysis of several models of BCL-2 protein shall be made in order to provide a better understanding of how our method works to the many structures obtained through NMR. As shown in results, the binding site Met 1 of ubiquitin was not found due to absence of hydrogens in the first amino acid of the analysed protein, which has misled into a wrong electrical potential of the Met 1 residue. Hence, next studies will seek to include adding/removing hydrogens algorithm in order to take into account the pH range and enhance the mapping of molecular potential surface. This will make the study more realistic, and the scoring function can be used to test other types of ligands. In order to improve the method and wash out the false positives, we are conducting studies to take into account the electronic density on the molecular surface based on quantum chemistry [50]. In addition, we will include in future work a molecular dynamic approach [51] in order to see how our method deals with structures in motion. Therefore, MSProt had a better prediction of cisplatin and transplatin binding-sites than HexServer and PatchDock methods, which provide a more precise insight to assist in new drugs designing.
We thank Jose R. Ruggiero for helpful discussions and comments. This work was supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq).