Journal of Proteomics & Bioinformatics
Open Access
ISSN: 0974-276X
ISSN: 0974-276X
Research Article - (2013) Volume 6, Issue 7
The classification of the structures of proteins provides preliminary information for the further detailed theoretical analyses. Classified information of protein folds might be utilized for the structural alignment while fold class prediction might help ab inito prediction of protein structures. Here, prediction of structural fold class of proteins with torsion angle based secondary structure profile library and multi-class linear discriminant analysis was performed. All-versus-all method was utilized to circumvent the problem of data imbalance of one-versus-others approach. From nonredundant structure files, a tripeptide secondary structure profile library was constructed and used to calculate the probable secondary structure content of protein folds. The mean and covariance matrices of the reference classes of the training set were derived using this library. Based on this information, fold classes of test set proteins were predicted using multi-class linear discriminant analysis. The result was highly accurate according to the low error rates. This highly accurate fold class prediction might be further utilized in the application of secondary structure predictions exploiting the benefits of larger scrutinizing windows. Appropriateness of the torsion angle representation in local structure analysis has also been partly proved.
Keywords: Protein fold classification; Linear discriminant analysis; Backbone torsion angle
Protein structure is determined by experimental methods including X-ray crystallography and NMR. There are about 83000 structures in the repository of Protein Data Bank as of August, 2012. However, this number still lags from the number of revealed protein sequences of more than 1 million. Analysis of experimentally determined structure and theoretical modeling of three-dimensional structure from protein sequence are, thus, fields of strong concern in computational biology. There exist many types of discrimination methods including homology searches and local structure delineations. The classification of the currently known structures of proteins provides preliminary information for the further detailed theoretical analyses. Classified information of protein folds might be utilized for the structural alignments while fold class predictions might help ab inito prediction of protein structures.
Protein local structure adopts typical secondary structural topology within the specific region of the whole protein. These structures usually adopt cork-screw like helical structure or zig-zag patterned extended structures while any other structures are called as “others” structure. The most common helical structure is α-helix, while the most common extended structure is β-strand. Many protein structure databases, including PROSITE [1-3], PRINTS [4], Blocks [5], Pfam [6], ProDom [7], SCOP [8], CATH [9], InterPro [10] and Swiss-Prot [11], refer information of the local secondary structure as important criteria for classification. Most of common protein structure databases classify folds according to the content of α-helix and β-strand structure as all-α, all-β, and α-and-β in the top level of the hierarchy. SCOP [8] is the hierarchical structure database with Class, Fold, Superfamily and Family levels. SCOP classifies folds into all-α, all-β, α/β, and α+β classes, where α/β and α+β classes are different in their matter of segregation of α and β structural moieties.
While most of the classifications of folds are conducted based on the observation of experimentally determined structures, protein fold structure classes are usually anticipated from sequence properties including amino acid composition, hydrophobicity, polarity, and van der Waals volume. Recently, Ding and Dubchak [12] devised support vector machine and neural network method to predict fold class from sequence data and Tan et al. [13] applied ensemble learning algorithm to the prediction of the fold class. Ding and Dubchack [12] tried to remedy two classes (one-versus-others) approach by additionally utilizing all-versus-all model of multiclass discrimination method. Most datasets would be imbalanced in one-versus-others approach in multi-class problems for discriminations and this imbalance would contribute to the poor accuracy as typically in the case of decision trees. Tan et al. [13] investigated if their ensemble learning classifier would show improvements for imbalanced datasets and if pattern level combination of data would be useful.
The three dimensional structure of proteins are possible to be represented with torsion angle system. The conformational change of proteins follow rotational movements along covalent single bond axes for the lack of significant change of the length and angle of covalent bonds for high energy barriers. The topology of the backbone of proteins could be relatively represented with backbone torsion angles only. The robustness of structural representation of proteins using backbone torsion angles was partly presented with previous structure alignment study [14]. Here, all-versus-all approach using multiclass LDA (Linear Discrimination Analysis) was conducted for secondary structural fold class predictions (Figure 1). Three-dimensional atomic coordinates from PDB (Protein Data Bank) and classification of the SCOP database were utilized for the training and validation of the algorithm. Backbone dihedral angle values were obtained from this information and applied to find the probable secondary structure content of protein folds. This new approach performs LDA on query folds referring mean and covariance matrices of secondary structure contents of reference classes. Fold class anticipations usually yield better accuracy in the predictions than residue-wise anticipations for the consideration of much larger numbers of informative sites. The better accuracy of fold class discriminations might support the validity of the consideration of longer segments in the secondary structure predictions. New method that predicts secondary structure using backbone torsional characteristics and LDA could be developed by utilizing the merit of longer segments for frame shifting window.
Figure 1: Flow diagram of the process of secondary structural fold class prediction. The flow of the secondary structural protein fold class prediction is described. An 8000 (203) tripeptide library of the probable secondary structure content was built from non-redundant PDB entries. Training sets of all-α, all-β and others (α+β) class members were collected referring SCOP classifications. Relevant PDB entries were used to generate information of the reference classes. LDA was conducted using the covariance matrices of reference classes and the secondary structure content of a query protein. Accuracy analysis as error rate calculation was conducted after the prediction of the secondary structural fold class by LDA.
Prediction of the fold class of proteins was performed based on the tripeptide secondary structure profile library which was constructed from non-redundant protein structures. The probable secondary structure content of each protein of training set and validation sets was predicted from this library. The mean and covariance matrices of the reference fold classes of the training set were derived from the probable secondary structure content of proteins of each class. Based on this information and the probable secondary structure content information of query proteins, classification of the fold class of a protein was conducted using multi-class LDA. The error rate and accuracy was measured for the validation sets from SCOP domains and CASP7 target models.
Secondary structure classification based on backbone torsion angles
The φ angle is the torsion angle of C-N-Cα-C atoms of protein backbones. The ψ angle is the torsion angle of N-Cα-C-N atoms of protein backbones. Secondary structure determination for each residue of training and validation set proteins was conducted referring the predicted characteristics derived from these two backbone torsion angles of non-redundant structures. Calculation of the torsion angle of A-B-C-D exploited the inner product of the normal vectors of the planes of A-B-C and B-C-D. The secondary structure of an amino acid residue was classified as α-helix if the backbone torsion angles belong to the range of (φ, ψ)=(-155°~-47°, º-62°~-52°), (-104°~-47°, -52°~-37°) and (-117°~-104°, -52°~-37°). A residue was classified as β-sheet secondary structure if the backbone torsion angles belong to the range of (φ, ψ)=(-155°~-138°, 90°~155°), (-140°~-64°, 90°~180°) and (-64°~-53°, 90°~100°) or 110°~168°). Residues of backbone torsion angles belonging to other ranges were considered to be others secondary structures. Typical Ramachandran plot was exploited for the classification scheme of the secondary structures.
Tripeptide secondary structure profile library
Amino acid trimer secondary structure profile library was constructed for the calculation of probable secondary structure content from the sequence of proteins of training set and validation sets. Profile of each tripeptide consists with three values of percent content of each secondary structure of α-helix, β-sheet, and others. Among many possible values of k for the k-mers, tripeptide was chosen by considering both the wealth of information and the amenability of smallness. The dihedral angles of the bonds between amino acids of tripeptides were first calculated. Tripeptides were collected from the proteins of PDB database with sequence homology of 90% or more were removed. The dihedral angles of numerous tripeptides were averaged for each case of occurrences. Thus, each case of tripeptide has average value of dihedral angles. This dihedral angle was used for the classification of the secondary structure of the middle residue of the tripeptide. The tripeptides with known secondary structure of the middle residue were used for the assignments of the secondary structures of the residues of a protein fold following the correspondence of the types of tripeptides. The proportions of a secondary structure within a fold were, then, used for the multiclass linear discriminant analysis.
LDA for classification of protein secondary structure
Protein fold class prediction was performed using multi-class LDA with probable secondary structure content variables, which was derived from backbone torsion angles. Each protein has three types of variables of α-helix (S1), β-sheet (S2), and others content (S3). A reference class with members of folds has means of S1, S2, and S3 values and a covariance matrix derived from these variables. Multi-class LDA was used to determine to which reference group an unknown protein belongs. LDA is a type of multivariate analysis that enables the statistical discrimination of a query group among multiple reference groups. This analysis utilizes the assumptive normal distribution of the Mahalanobis distances of observations of reference groups. The classification of queries of unknown groups can be performed with this statistical method [15].
Secondary structural content are represented in the form Si,j, where i and j denote the observation number and secondary structure content type (α-helix (1), β-sheet (2), and others (3)), respectively. Three variables of secondary structure content of a fold were calculated as the sums of respective contents from trimer library that corresponds with the sequence of a given fold. Two flanking terminal residues which are impossible to be matched into the trimer secondary structure profile library as the middle residue were omitted in this process. The matrix of secondary structure content of group k with l entries is as follows, where k denotes the number of each of the three groups of α-fold (1), β-fold (2) and others-fold (3).
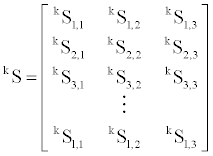
Each group has three-dimensional average vectors of secondary structure content. Calculation of mth element of average vector of group k with l elements is as follows,
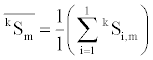
where m denotes the type number of secondary structure content of α-helix (1), β-sheet (2), and others structure (3).
Covariance of variables of each group is needed for the calculation of the Mahalanobis distance. SAS (ver. 9.1) was used for the calculation of covariance of each group. The averages calculated as described above were used for the calculation of the covariance values. Each entry of the covariance matrix of the reference group k is calculated as follows,
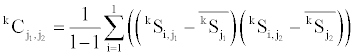
where j1 and j2 denotes the type of the secondary structure content variable. The square of the Mahalanobis distance (D2) of an observation from the reference group k is as follows,
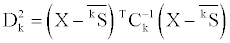
where X is a three-dimensional vector of the secondary structure content of an observation, kS is the mean vector of the secondary structure content and Ck is the covariance matrix of group k. Under the assumption of normal distribution of the Mahalanobis distances of observations, the likelihood of an observation to belong to the reference group k is as follows,
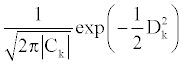
LDA assumes the covariance matrices to be identical among the reference groups. Thus, the comparison of likelihood may be reduced into the comparison of the squares of the Mahalanobis distances by applying logarithm and numerical operations. Here, the group to which a protein belongs was determined as the group that shows the lowest D2 value. The accuracy of the discrimination function can be calculated with the error rate (ERR) which is the probability of misclassification which can be expressed as follows,
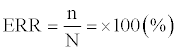
where n signifies the number of proteins that are erroneously predicted out of N total predictions. The accuracy (ACC) of protein secondary structure prediction is also measured as follows,
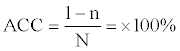
LDA analyses and calculations were conducted with codes written in JAVA language.
Data sets
SCOP folds of all-α class were classified into α-fold group and folds of all-β class were classified into β-fold group. DNA-containing files were omitted among the 7621 all-α structures and the 10,047 all-β structures. 11,037 domains of the α+β SCOP class were classified into others-fold group. The α+β class was used as the reference for the others class because of their rather even helix/extended/others content. A similar class of α/β was omitted to level the number of entries among the reference classes. 50 folds from each of these three reference groups were used for the validation set. 90 SCOP folds from 42 proteins of CASP7 models were also used to test the accuracy.
Fold class prediction of proteins was performed using a tripeptide secondary structure profile library based on backbone torsion angles with LDA. Each query protein of the validation sets was assigned to α-fold, β-fold or others-fold class. The result was highly accurate with low error rate of the classification of validation sets. General concordance between secondary structure content and the assigned fold class was observed in α-fold and β-fold classes. Insignificant inclination toward any specific secondary structure of α-helix and β-sheet was observed in the others-fold class.
Backbone torsion angle based prediction of probable secondary structure content
The magnitude of the percent contents of the probable secondary structures of each of α-helix and β-sheet of query folds showed a highly concordant tendency to the corresponding classes. The α-fold class proteins showed a much higher proportion of α-helix structures than β-sheet structures, and the β-fold class showed a much higher proportion of β-sheet structures than α-helix structures. The othersfold class of SCOP α+β class, however, showed rather even proportions of the three types of secondary structure. These rather common results partly suggest that the secondary structure classification based on backbone dihedral angles is appropriate. Test set proteins with rather high others secondary structure content were classified as others-fold class for its longer distance from α-fold class and β-fold class originated from the large difference from the mean α-helix and β-sheet contents of each class.
Prediction of fold classes using LDA
LDA was performed with the predicted percent content values of the secondary structures of a query fold and mean values and covariance matrices of the probable secondary structure contents of reference classes. The predictions of secondary structure contents of both the query and reference group proteins were made referring the 8000 (203) tripeptide secondary structure profile library. LDA of the validation set was performed and showed high accuracy with a very low error rate of 6.67% (i.e. accuracy of 93.33%; Table 1). Ten erroneous classifications were observed from the test set of 150 SCOP test folds. Similar results of error rate of 8.89% (i.e. accuracy of 91.11%) were observed from the analysis of the 90 SCOP folds from 42 proteins of CASP7 targets (Table 1). Eight erroneous classifications were observed out of 90 folds in this test set. Mean accuracy of 92.5% was observed from the total of 240 test queries. This high accuracy may have partly originated from the rather concentrated distribution of secondary structure proportions of the folds to the mean values of each corresponding group. The high accuracy of the prediction also arises from the accurate representation of the tripeptide secondary structure profile library of the states of local structures. This also indicates that secondary structure states of tripeptides are rather conserved. A more detailed reference profile library including longer peptide library and Markovian library with series of tripeptides might be helpful to improve incorrect protein structure class predictions. Iterative k-fold or leave k-out validations were not performed considering the narrow distribution of secondary structure contents among the members of the three fold classes.
| Validation set | Error proportion* | Error rate (%) | Accuracy (%) |
|---|---|---|---|
| Spared training set | 10/150 | 6.67 | 93.33 |
| CASP7 set | 8/90 | 8.89 | 91.11 |
| total | 18/240 | 7.5 | 92.5 |
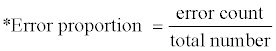
Table 1: Result of class predictions of validation sets using LDA.
The percent accuracy of this fold class prediction and the Q3 values of the secondary structure predictions of numerous methods are compared in Table 2. EVA server results of the accuracies of secondary structure prediction algorithms of DBNN, which uses dynamic Bayesian networks, PSIPRED, JPRED, PHD, and PROSITE, which uses DA (Discriminant Analysis), are illustrated in Table 2 [16]. The mean percent accuracies of fold class predictions from the validation set of 150 folds and 90 CASP7 target folds were also listed in the Table 2 for comparison. The higher accuracy of the fold class predictions than typical secondary structure predictions might be responsible for the larger scope of the reference of information. Secondary structure prediction generally concerns about 5 to 10 local residues to determine the local structure of a single amino acid residue. The classification of a fold, however, usually incorporates information on more than 50 residues. This point is also possible to be explained in terms of probability. Average tendency of 60% and 70% of α-helix would signify a definitively different fold of odds ratio in the case of long polypeptides according to the multiplied probability with Markovian dependency, while it would be similar in the local structure prediction of short amino acid residues. The error rate might be reduced by the larger difference in actual probability from the same average tendency difference in the case of fold-wise predictions. The better accuracy of fold class prediction possibly implies the benefit of larger scope of the analysis window. The high accuracy of this fold class prediction method also partly signifies the appropriateness of the backbone torsion angle system for the representation and analysis of local structures. The method of LDA with backbone dihedral angles might be utilized in the secondary structure predictions by focusing into the vicinity of the subject residues while exploiting the scheme of larger windows than those in typical algorithms.
| Method | Q3 (%) | Accuracy (%) |
|---|---|---|
| Secondary Structure Prediction | ||
| DBNN | 77.8 | |
| PSIpred | 77.8 | |
| PROFsec | 76.7 | |
| PHDpsi | 75.0 | |
| PROSITE | 78.0 | |
| Fold Class Prediction | ||
| Backbone Torsional Tripeptide Library LDA | 92.5 |
Q3: three-state per-residue accuracy (percentage of correctly predicted residues)
Table 2: Performances of torsional LDA fold class prediction and residue structure predictions.
Although structural studies of proteins have been an area of concern for more than 50 years, the accuracy of predictions has been limited to certain degrees despite of scientific and technological developments and various statistical applications. Considering that correct secondary structure anticipation is quite necessary for the prediction of the threedimensional structure of proteins, the limitations of the accuracy of the secondary structure prediction might be considered to be the one that makes the decipherment of biological phenomena difficult. A library of α-helix, β-sheet and others secondary structure profile of 8000 (203) tripeptides was constructed referring the backbone torsion angles. Trimer polypeptide was selected considering both the wealth of information and amenable smallness. Nonredundant PDB entries with 90% sequence similarity cutoff were used to calculate backbone torsion angles to build the secondary structure profile library of the central residue of 8000 tripeptides. The proportions of three secondary structures of folds from validation sets and reference set were predicted using this library. The mean and covariance matrices were derived for each of the three reference fold classes from the predicted secondary structure proportions. LDA was exploited for the prediction of fold classes of queries from test sets. In the present study using LDA, the classification of query folds with unknown structure showed an accuracy of over 90%. Erroneous classifications of the members between α-fold and β-fold classes were rare, while the misclassifications of the othersfold group was more frequent, partly indicating the necessity of more definite references for the others-fold class.
The fold class prediction might be applied to the secondary structure prediction with modifications and also might be utilized in the prediction of the tertiary structure of a protein. Secondary structure prediction methods have been used in the prediction of tertiary structure by predicting local topologies, which partly indicates the importance of secondary structure information in numerous fields of theoretical biology. Three-dimensional structure information of protein might be exploited for the anticipation of protein functions and other relevant properties, including protein-protein interactions. Secondary structure and fold class information also could be utilized in the prediction of diverse biological phenomena including epidemiological issues. Knowledge based anticipation of the possibility of zoonosis [17] based on the property of host cell receptors might utilize local and fold-wise secondary structure properties. Anticipation of pandemic outbreaks might also utilize the secondary structural properties of host cell receptor proteins. Further study based on our work might perform the secondary structure predictions implementing the benefit of larger scope of scrutinized residues, which might be helpful for relevant protein structural studies.
This work was supported by the NRF (National Research Foundation of Korea) grant funded by the Korean government, MSIP (Ministry of Science, ICT and Future Planning, No. 2012008344). This research was also supported by the NRF funded by the MSIP (No. 2012M3A9D1054622). Support from KISTI (Korea Institute of Science and Technology Information, K-13-L01-C02-S04) is gratefully acknowledged.