Journal of Geology & Geophysics
Open Access
ISSN: 2381-8719
+44 1478 350008
ISSN: 2381-8719
+44 1478 350008
Research Article - (2014) Volume 3, Issue 3
The quantitative evaluation of carbonate reservoir is one of the key issues of oil and gas exploitation. However, due to the characteristics of carbonate reservoir, such as diverse physical distribution, complex pore-throat structure and strong heterogeneity, its quantitative evaluation is relatively difficult. Take the Lei 1 Member carbonate reservoir of Middle Triassic Leikoupo Formation in the Moxi gas field of Sichuan Basin as the example. The improved analytic hierarchy process is adopted based on 9 prioritized parameters which have direct influence on the quality of carbonate reservoir, namely porosity, permeability, water saturation, displacement pressure, average pore-throat radius, effective reservoir thickness, permeability variation coefficient, permeability rush coefficient and permeability range, to build a multi-level hierarchical structure model and quantitatively determine the relative importance quantitative indicators of all the parameters for reservoir quality. And fuzzy comprehensive evaluation method is used to build a quantitative evaluation model of carbonate reservoir. The evaluation results are well consistent with the actual gas capacity, which indicates that the mathematical model is available for quantitatively evaluating the carbonate reservoir and has relatively good feasibility.
Keywords: Multi-level, Fuzzy theory, Quantitative evaluation, Carbonate reservoir, Leikoupo formation, The Moxi gas field of Sichuan Basin
With the development of reservoir geology, the trend of reservoir evaluation is to realize the combination of “qualitative and quantitative” aspects, “macro and micro” aspects as well as “general and specific” aspects [1,2]. Due to the characteristics of carbonate reservoir, such as diverse physical distribution, complex pore-throat structure and strong heterogeneity [3], its quantitative evaluation is relatively difficult. Take the Lei 1 Member carbonate reservoir of Middle Triassic Leikoupo Formation in the Moxi gas field of Sichuan Basin as the example, and the physical property, pore-throat structure, effective reservoir thickness and heterogeneity of carbonate reservoir are comprehensively considered. The improved analytic hierarchy process is adopted based on 9 prioritized parameters which have direct influence on the quality of carbonate reservoir, namely porosity, permeability, water saturation, displacement pressure, average pore-throat radius, effective reservoir thickness, permeability variation coefficient, permeability rush coefficient and permeability range, to build a multi-level hierarchical structure model and quantitatively determine the relative importance quantitative indicators of all the parameters for reservoir quality. And fuzzy comprehensive evaluation method is used to build a quantitative evaluation model of carbonate reservoir, achieving the purpose of quantitatively evaluating the quality of Lei 1 Member carbonate reservoir in study area.
The Sichuan Basin is a diamond-shaped structural-sedimentary Basin in southwest China [4]. It is situated between the longitude 103°45’~108°43’E and the latitude of 28°42’~33°03’N. It includes eastern Sichuan and western Chongqing, covering an area of approximately 19×104km2. The Moxi gas field is located in the central low-flat belt of the Sichuan Basin, trending roughly in northeast to southwest (Figure 1a) [4]. It has succeeded in gas exploration and exploitation since the first well drilling of Moshen 1 in 1977 (Figure 1b). The gas production and proven reserve is about 4.0×108m3 per year and 3.3×1010m3, respectively [4]. The Middle Triassic Leikoupo Formation belongs to marine deposits and can be divided into four lithologic stages ranging from Lei 1 Member to Lei 4 Member [5]. Lei 1 member (in the lower part) is mainly constituted by unequal-thickness limestone, dolomite and gypsum rock interbeds, ranging from 0-100 meters. It can be further subdivided into two sub-members, namely Lei 11 sub-member and Lei12 sub-member. At the bottom of Lei 11 submember, datolite acts as the boundary with the underlying Low Triassic Jialing jiang Formation. And the lower part of Lei 11 is the unequalthickness interbeds of dark gray massiveness, lamellar anhydrock and argillaceous dolomite, and pelitic dolostone.
Figure 1: (a) Tectonic units in the Sichuan Basin and the location of the Moxi gas field. (b) Some representative wells in the Moxi gas field. (c) Generalized stratigraphy of the Moxi gas field.
The middle and upper parts is consisted of light gray-brown grain limestone and brown gray-khaki sparry grain dolostone, with reservoir mainly developed in grain dolostone (Figure 1c). The carbonate reservoir is the main target for gas exploitation in the Lei 1 Member of Leikoupo Formation in the region.
According to the basic idea of fuzzy theory, the main factors that influence the reservoir quality are reasonably selected (i.e. build the factor set), and appropriate weight is allocated to these factors (i.e. build the weight set). Based on a certain evaluation rule (i.e. build the evaluation set), the appropriate membership function is chosen to get the grade of membership after trail calculation. And the prioritization principle is adopted to select the objects with high grade of membership and abandon the ones with low grade of membership, so that the comprehensive evaluation model for carbonate reservoir can be built and the quantitative evaluation for the reservoir quality can be made (Figure 2).
Figure 2: The quantitative evaluation model of carbonate reservoirs.
The improved analytic hierarchy process is adopted to determine the weight. The improved AHP inherits the method of the traditional analytic hierarchy process that the thinking process is mathematized, which not only simplifies the systematic analysis and calculation, but also helps the decision-maker maintain the consistency of his thinking process. When the importance of 2 factors is compared in the judgment matrix, 3 scales method (i.e. (0, 2) scale method) judgment which is easily provided by people is adopted to replace the 9 scales judgment which is hard provided through the traditional analytic hierarchy process exactly [6-9]. This has solved the tedious process of the traditional analytic hierarchy process that uses 1-9 scale method to build the judgment matrix. And for the test method of results, sub optimal matrix is obtained through the optimal transmit of the judgment matrix. In this way, the repeated checks of consistency, which is required by the traditional analytic hierarchy process and results in constant adjustments of the judgment matrix, have been avoided. Therefore, the importance of all the factors can be objectively determined in the reservoir evaluation, the weight coefficient can be appropriately obtained, and the weight set can be successfully built.
Defining factor set
With the physical properties, pore-throat structure, effective reservoir thickness, heterogeneity and other factors of carbonate reservoir being considered, priorities are given to 9 parameters with direct influence on the quality of carbonate reservoir so as to build the factor set, including porosity (?), permeability (k), water saturation (Sw), displacement pressure (Pd), average pore-throat radius (r50),effective reservoir thickness (H), permeability variation coefficient (VK), permeability rush coefficient (TK) and permeability range (JK).
Porosity (? ) and permeability (k) can reflect the physical nature of the reservoir rock in the reservoir; water saturation (Sw) can indicate the water-containing condition, which has certain impacts on the oilgas capacity of the reservoir; displacement pressure (Pd) and average pore- throat radius (r50) can reflect the characteristics of microcosmic pore-throat structure; effective reservoir thickness (H) has important impacts on the oil-gas capacity of the reservoir; permeability variation coefficient (VK), permeability rush coefficient (TK) and permeability range (JK) can show whether the heterogeneity within the reservoir is strong or weak [10-12].
Thus, the factor set U of quantitative evaluation for carbonate reservoir can be built (Equation 1):
U = (u1 u2 u3 u4 u5 u6 u7 u8 u9) = (?, k,Sw, Pd, r50, H, VK, TK, JK), n=9 (1)
Defining the weight set
Weight refers to the influence level of each evaluation factor on the carbonate reservoir quality, or the contribution value of each evaluation parameter to a certain reservoir system [13-15].
The improved analytic hierarchy process is adopted to determine the weight coefficient of all the factors, and steps of building the weight set are shown as follows (Figure 3)
Figure 3: Flow chart of weight coefficients calculation.
Step One: build a multi-level analytic hierarchy model.
The main purpose of building the analytic hierarchy model is to make the systematic problem hierarchical, which means the problem will be separated into different component factors according to its nature and the overall goal needed to be achieved. The factors will be aggregated in different levels according to the mutually related influence and the membership relationship among the factors, so that a multi-level analytic hierarchy model can be built. Among them, the levels include: goal level, the highest criterion level, middle level (maybe several ones) and the lowest level.
The participating parameters, namely porosity (?), permeability (k), water saturation (Sw), displacement pressure (Pd), average pore-throat radius (r50), effective reservoir thickness (H), permeability variation coefficient (VK), permeability rush coefficient (TK) and permeability range (JK), are defined as sub-criterion level C; physical properties, pore-throat structure, sedimentary factor and heterogeneity are defined as the criterion layer B; and evaluation of carbonate reservoir is defined as the goal level A. Therefore, the evaluation hierarchical structure model for carbonate reservoir can be generated (Figure 4).
Figure 4: The hierarchical structure model ofcarbonate reservoir evaluation.
Step Two: build a judgment matrix
3 scales method (or (0, 2) scale method) is adopted to build the judgment matrix. When the factor i and factor j are compared with each other, 2 means that factor i is more important than factor j; 1 means that factor i is as important as factor j; and 0 means that factor i is less important that factor j. The form of judgment matrix θij (Equation 2) is built as follows:
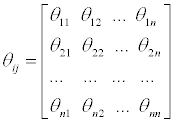(2)
Where
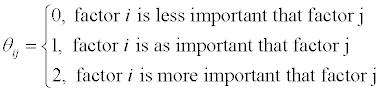
And when θij =1 , it means the factor has equivalent importance compared with itself.
Step Three: strike the sub optimal matrix and eigenvectors of the judgment matrix
After the obtained judgment matrix θij is processed as the optimal transmit and sub optimization, the sub optimal matrix θij’ of the judgment matrix θij can be obtained. The processing formula of sub optimization is shown as follows (Equation 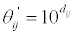3):
(3)
Where,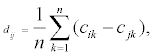 
cjk and cjk respectively indicate the Line k optimal transmit results of the judgment matrix θij
The eigenvector Wi of sub optimal matrix θij’ can be obtained through square root method. And the calculation formula is shown as follows (Equation 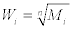4):
(4)
Where,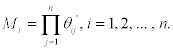 
Step Four: strike the weight through multi-leveled overall ranking.
To calculate the accumulated weight of factors in each level with respect to the goal level means to calculate the weight of factors in each level through multi-level overall ranking. The process is carried out from the highest to the lowest. The weight eigenvector obtained through the improved analytic hierarchy process will be processed by normalization to strike the weight coefficient of each factor in the reservoir quantitative evaluation and to build the weight set A.
Defining evaluation set
According to the industrial standard for the quality classification of oil and gas reservoir in China [16], which classifies reservoir quality into 4 categories, the evaluation set is built V (Equation 5).
V = (I, II, III, IV) (5)
Where, I, II, III and IV represent good reservoir, relatively good reservoir, ordinary reservoir and bad reservoir respectively.
Defining the membership function
During the fuzzy evaluation process of carbonate reservoir, the final influence of each factor on reservoir quality can be indicated by its grade of membership for the reservoir quality. And the premise of getting the grade of membership is to define an appropriate membership function [17,18].
Currently, the membership functions usually used by scholars include “rectangular distributed function”, “trapezoidal distributed function”, “Cauchy distributed function”, “concave-convex distributed function”, “ridge-shaped distributed function”, etc... After many times of test calculation, the “middle ridge-shaped distributed function” is adopted as the membership function for the quantitative evaluation of carbonate reservoir, and the equation μA(x) is shown as follows (Equation 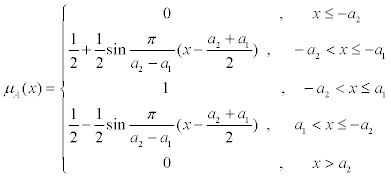6):
(6)
The distribution curve of the “middle ridge-shaped distributed function” is shown in the following (Figure 5):
Figure 5: The middle ridge-shaped distributed function.
Building fuzzy relation matrix
The fuzzy relation matrix R is determined and constituted by the membership grade rij ( i=1,2,... n; j = 1,2,...m ) of the ith sample for the reservoir quality, with the effects of the ith evaluation factor:
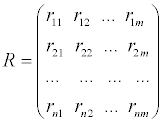(7)
R is the fuzzy relation between evaluation factors and results, through which the evaluation factors can be turned to evaluation results [17,18].
Comprehensive evaluation
Because the status of each factor may be unequal, each factor needs to be weighted so as to be combined with R, which constitutes the comprehensive evaluation of each factor. According to the compound operation of matrix, an variation has been determined by R: after a fuzzy subset A is given to U based on the actual data, a fuzzy subset can be determined for B, namely fuzzy comprehensive evaluation mode B (Equation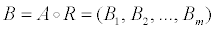8):
(8)
According to the processing method of fuzzy comprehensive evaluation method for evaluation indicator, the method of maximum membership grade is adopted for processing the evaluation factors, which means the element Vj in evaluation set corresponded to the maximum evaluation indicator Max (Bj) is taken as the evaluation result [17,18].
Case Study
Take the Lei 1 Member carbonate reservoir of Middle Triassic Leikoupo Formation in China’s central Sichuan Basin as the example, and the quantitative evaluation is carried out for Lei 1 Member carbonate reservoir of the single well in the study area to analyze the application of the evaluation model in the quantitative evaluation of carbonate reservoirs.
Defining the factor set and weight set
The factor set is built according to Equation 1, namely the evaluation factor set U of carbonate reservoir. Then, the weight coefficients of all the parameters are defined based on the improved AHP, as shown in the Table 1.
| u1 | u2 | u3 | u4 | u5 | u6 | u7 | u8 | u9 | |
| U | ϕ | k | Sw | Pd | r50 | H | VK | TK | JK |
| Ai | 0.15 | 0.14 | 0.13 | 0.11 | 0.13 | 0.12 | 0.09 | 0.07 | 0.06 |
Table 1: Factor Set and Weight Set.
Defining the evaluation set
The evaluation set V is built according to Equation 5, which classifies the quality of carbonate reservoir in the study area into four categories.
Defining the membership function
Based on the industry standard for quality classification of oil and gas reservoirs and combined with the carbonate reservoirs of Lei 1 Member in the Moxi gas field, the optimal statistical classification method is adopted to get the evaluation standards for various kinds of reservoirs, as shown in Table 2. The factors with positive correlation with the reservoir quality (including porosity (? ), permeability (k), average pore-throat radius (r50), and effective reservoir thickness (H)) are obtained through “rising part of ridge-shaped distributed function”; and the factors with negative correlation with reservoir quality (including water saturation (Sw), displacement pressure (Pd), permeability variation coefficient (VK),permeability rush coefficient (TK)and permeability range (JK)) are obtained through “descending part of ridge-shaped distributed function ”.
| Evaluation Parameter | Category I Good Reservoir | Category II Relatively Good Reservoir | Category III Ordinary Reservoir | Category IV Bad Reservoir |
|---|---|---|---|---|
| ϕ( % ) | >12 | 8-12 | 4-8 | <4 |
| k(×10-3μm2) | >10 | 1-10 | 0.1-1 | <0.1 |
| Sw(%) | <10 | 10-30 | 30-50 | >50 |
| Pd (MPa) | <4 | 4-8 | 8-12 | >12 |
| r50 (μm) | >0.5 | 0.3-0.5 | 0.1-0.3 | <0.1 |
| H (m) | >10 | 4-10 | 1-4 | <1 |
| VK | <0.4 | 0.4-0.8 | 0.8-1.2 | >1.2 |
| TK | <2 | 2-3 | 3-4 | >4 |
| JK(after logarithm) | <0.5 | 0.5-1 | 1-2 | >2 |
Table 2: Fuzzy Comprehensive Evaluation Standard of Lei 1 Member Carbonate Reservoir, Moxi gas field.
For example, the membership function of porosity (?) which has positive correlation with the reservoir quality is shown as follows:
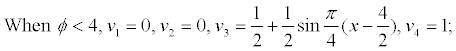
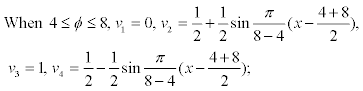
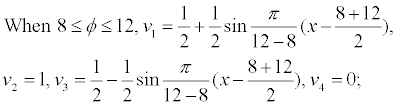
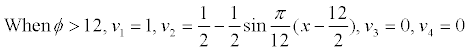
The membership function of displacement pressure (Pd) which has negative correlation with the reservoir quality is shown as follows:
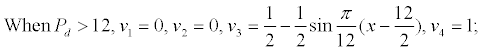
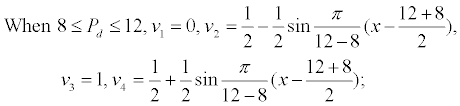
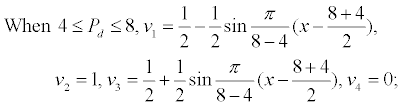
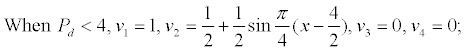
Building fuzzy relation matrix
Take the data of Lei 1 Member carbonate reservoir of Well Mo22 in the Moxi gas field as the example, and Equation7 is adopted to build the fuzzy relation matrix R as follows (Table 3):
| Parameters | ϕ | k | Sw | Pd | r50 | H | VK | TK | JK |
| Data | 13.72 | 5.74 | 9.25 | 5.4 | 0.37 | 3.8 | 0.22 | 1.6 | 0.72 |
Note: ϕ -%, k -×10-3μm2, Sw -%, Pd - Mpa, r50 -μm, VK, TK - dimensionless value, JK - numerical value after the Logarithmic process.
Table 3: Original Data of Lei 1 Member Carbonate Reservoir of Well Mo 22.
Fuzzy comprehensive evaluation
According to the fuzzy comprehensive evaluation Equation 8, the fuzzy comprehensive mode B is generated: B = A? R
According to the method of maximum membership grade, the Lei 1 Member carbonate reservoir of Well Mo22 is evaluated as the relatively good reservoir, belonging to Category II. Similarly, the Lei 1 Member carbonate reservoir quality of other wells in the Moxi gas field can also be identified (Figure 6).
Figure 6: Quality Evaluation Result of Lei 1 Member Carbonate Reservoir of Wells, Moxi gas field.
Inspection on the evaluation results
Comparison is made between the results of reservoir quantitative evaluation and the actual oil-gas capacity in the Moxi gas field. And the Figure 7 shows the Lei 1 Member carbonate reservoir reservoir daily gas production of representative wells. From the figure, Well Mo 41, Well Mo 22 and Well Mo 24 have relatively good capacity, and they are evaluated as the Category I (good reservoir) or Category II (relatively good reservoir) according to the evaluation results; the Well Mo 205 has ordinary capacity, and it is evaluated as Category III (ordinary reservoir) according to the evaluation results; the capacity of Well Mo 005-2 and Well Mo 27 is relatively bad, and they are evaluated as Category IV (relatively bad reservoir) according to the evaluation results. These reflect that the actual oil-gas capacity is consistent with the result of quantitative evaluation.
Figure 7: The Lei 1 Member carbonate reservoir reservoir daily gas production of representative wells, Moxi gas field.
(1) The carbonate reservoir quantitative evaluation model of multi-level fuzzy theory is built to evaluate carbonate reservoir. The improved analytic hierarchy process is adopted based on 9 prioritized parameters which have direct influence on the quality of carbonate reservoir, namely porosity, permeability, water saturation, displacement pressure, average pore-throat radius, effective reservoir thickness, permeability variation coefficient, permeability rush coefficient and permeability range, to build a multi-level hierarchical structure model and quantitatively determine the relative importance quantitative indicators of all the parameters for reservoir quality. And fuzzy comprehensive evaluation method is used to build a quantitative evaluation model of carbonate reservoir.
(2) The carbonate reservoir quantitative evaluation model of multilevel fuzzy theory is feasible because its results are consistent with actual oil-gas capacity of Lei 1 Member carbonate reservoir in the Moxi gas field.