Bland and Altman, (1986) introduced a useful graphical procedure for comparing two methods of measurement of a continuous biological variable. The Bland-Altman plot of differences (ordinate) versus means (abscissa) of paired measurements is simple and elegant, and has become a standard for agreement studies, especially when combined with limits of agreement. Typically, 95% limits of agreement lines are superimposed on the Bland-Altman plots; these provide an interval within which 95% of differences between future measurements by the two methods would be expected to lie.

If one wishes to compare more than two matched measurements, pairwise Bland-Altman plots can be shown. This might prove cumbersome, however, with increasing numbers of measurements being compared. Bland and Altman, (1999) and Bland and Altman, (2007) have proposed rigorous statistical methods for such studies, devolving from formal analyses of variance of the method comparison studies. Similarly, an informal graphical procedure is available from the quality control literature, namely, Shewhart control charts for the range (Shewhart, 1939; Montgomery, 2001). Conceptually, one plots the ranges (ordinate) versus the means (abscissa) of the matched samples for the range chart.

In this note, we describe range charts for multiplymatched comparison studies, and illustrate some techniques for imposing limits of agreement on the charts. We illustrate this method with data arising from a recent study we had undertaken, to investigate the reproducibility of raw mass spectrometry features of abundance, including spectral count, peptide number and ion intensity values, across replicate 2DLC mass spectrometry measurements.

Reference Intervals

In comparison studies of two methods, the limits of agreement advocated by Bland and Altman can be interpreted as reference intervals, and delineate the range within which most differences between measurements might be expected to lie. The reference interval is generally defined by the range between two centile values of a population, centered about the median value. For example, the standard limits of a 95% reference interval would be the 2.5th and 97.5th centiles.[See Altman and Bland,(1994) for some discussion of terminology regarding centiles, quantiles, and related quantities.]

There are many ways of constructing reference intervals, as elegantly summarized by Wright and Royston, (1999) and Bland and Altman, (2007). We here describe two simple nonparametric techniques, which make no assumptions about the underlying distributions of the data comprising the range charts, followed by a semi-parametric technique, related to underlying normality.

Harrell-Davis

Harrell and Davis (1982) introduced an elegant distribution- free quantile estimator, which may be invoked to estimate the centiles of an underlying distribution.

This approach is formulaically straightforward, but does require computational capabilities involving mathematical functions. For reference, we state Harrell and Davis's formula in the Appendix.

Bootstrap

A second nonparametric approach utilizes the bootstrap (Efron and Tibshirani, 1993), as an extension of the simple approach of estimating empirical centiles directly from the ordered observations. Draw, say, 1000 bootstrap samples of the same cardinality from the underlying observations. From each bootstrap sample, compute the desired empirical centiles, using interpolation if necessary between the nearest two order statistics. Then, average the corresponding empirical centiles over the bootstrap samples to establish the reference interval limits. This approach is computationally involved, but formulaically simple.

Box-Cox Transformation Procedure

Box and Cox, (1964) introduced a power function that has been widely adopted to transform data to approximate normality. In the present context, one would invoke the Box- Cox procedure on the sample ranges, determine limits of agreement on the Box-Cox transformed scale, and then back-transform to the original range scale. There is some computational complexity involved in finding the Box-Cox transformation parameter [see Appendix],but determination of limits of agreement on a putatively normal scale is straightforward.

An Application

We illustrate range charts and reference intervals with the following example. Yu and colleagues, (2008) have undertaken an extensive study of computational and statistical considerations relating to proteomic analyses of label-free mass spectroscopy (MS) data. We utilize one dataset from their study, consisting of normalized spectral indices of 174 peptides found in normal liver tissue from three replicate MS runs. Yu et al., 2008 investigate fundamental issues of reproducibility and effects of normalization in this and other datasets, and we make no attempt to recapitulate their analyses here. Rather, our use of range charts is meant to be complementary to their more comprehensive study.

In Figure 1, we give the range chart for the 174 replicates. Clearly, variability increases with sample mean, an important diagnostic from these plots. We may take a simple log transformation (Bland and Altman, 1986, Bland and Altman,1996) of the spectral indices, with the intent to render the variance independent of the mean. As shown in Figure 2, the log transform goes far toward ameliorating the increasing variability with mean in the original spectral data.

Figure 1: Range chart for spectral index measures from 174 peptides, as determined from three independent mass spectrometry runs. Red lines delineate a nonparametric 90% tolerance interval for future determinations.

Figure 2: Range chart derived from the log-transformed data described in Figure 1, along with nonparametric 90% tolerance intervals.

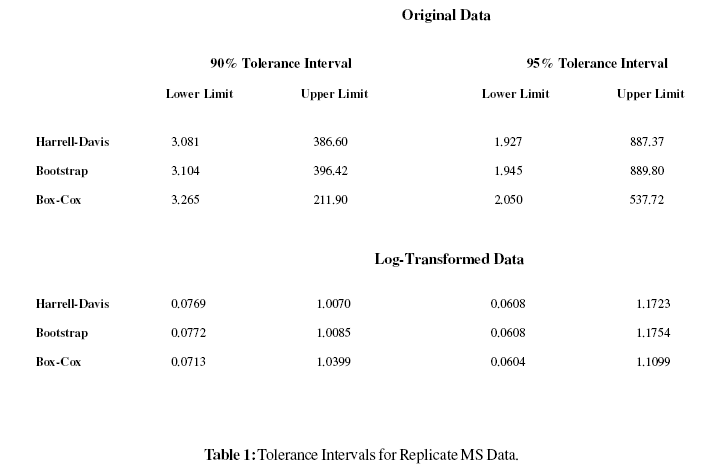
We turn next to the issue of tolerance intervals. In Table 1 we give the limits of the 90% and 95% tolerance intervals for the original data as well as the log-transformed data, for the three methods described earlier. That the Harrell-Davis and bootstrap estimates are nearly coincident is unsurprising: Sheather and Marron (1990) have noted the interconnection of the two methods. The Box-Cox method is somewhat deviant from the other methods, particularly in the upper limits for the original data. Here, there are 14 values (8.0%) exceeding 211, 7 (4.5%) exceeding 386 or 396, 5 (2.9%) exceeding 537, and 4 (2.3%) exceeding 887 or 889; the nonparametric approaches appear to have coverages nearer the desired levels of 5% or 2.5% than Box-Cox. We comment that with the original data, Box-Cox was not altogether successful in achieving normality: sample skewness was reduced from 5.27 to 0.004 (target 0), but sample kurtosis was reduced from 33.32 to 3.59 (target 3). Further correction for kurtosis might be desirable. In Figure 1and Figure 2 we have also superimposed the nonparametric twosided 90% tolerance intervals; again, the log transformation seems quite suitable.

Our motivation for investigating range charts was a comprehensive study we had undertaken, to investigate the reproducibility of raw mass spectrometry (MS) features of abundance, including spectral count, peptide number and ion intensity values, across replicate 2DLC mass spectrometry measurements. We found that typically raw features were not very reproducible across replicates. We could verify this formally via analyses of variance; our search for an informal graphical procedure led us first to Bland-Altman plots, and then to range plots as an appropriate extension to greater than two replicate runs. The range plots gave us immediate indication that log transformation would ameliorate the increasing variability problem. We went on to develop a more involved normalization technique which also tended to work well with our experimental data.

The reproducibility of a proteomics experiment can be viewed in two ways, 1) reproducibility in terms of the proteins identified, i.e., are we identifying the same proteins in replicate 2 as we did in replicate 1, and 2) reproducibility in the relative quantity of these proteins detected across the replicates, i.e., is the relative abundance of protein A the same in replicate 1 as in replicate 2. In terms of protein identification, Durr et al., (2004) previously showed that any second replicate "shotgun" MS measurement will identify 30-40% of proteins not found in a single MS measurement of an identical sample, inferring an approximate 60% overlap in protein identifications between replicate measurements. This also demonstrates the requirement for multiple replicate measurements in order to achieve significant coverage of the sample of interest; we refer the interested reader to Koziol et al., (2006), where we give some practical guidelines for experimental design. Nevertheless, the Yu et al.,2008 study clearly demonstrated [both formally and with range charts] that the abundance features for these common proteins are not very reproducible across replicate MS measurements. As a result, normalization of these features (by such method as developed by Yu et al., 2008) is required to control for the variation, which in turn enhances the reproducibility of the replicates thus allowing their direct comparison.

Range charts are conceptually straightforward, and are an economical way of depicting levels of agreement among multiple measurements. Compared to pairwise Bland-Altman plots, one range chart summarizes the entire agreement study; however, signed differences revelatory of systematic large or small values in one method compared to a second method may be obscured.

There are various ways of establishing reference intervals on range charts. We have focused on nonparametric and semiparametric methods that are relatively easy to implement, and dispense with sometimes restrictive distributional assumptions attending ranges. We mention in passing that we also explored quantile estimation based on Edgeworth and Cornish-Fisher expansions (Cornish and Fisher, 1937; Stuart and Ord, 1987), but results were less satisfactory than with Box-Cox. The distribution of the range with normally distributed random variables has been extensively studied, leading to parametric approaches to establishing reference intervals; see Montgomery, (2001) for details. And, one could plausibly impose one-sided limits of agreement with range charts, in settings where upper limits of agreement are of primary interest

We remark that, with two matched measurements, the range chart displays the absolute values of the signed differences from the Bland-Altman plot. This relationship generalizes to our setting of three MS determinations, a consequence of the mathematical identity: range{x₁, x₂, x₃} = ½ ( |x₁ - x₂| + |x₂ - x₃| + |x₃ - x₁| ), for any real numbers x₁, x₂, x₃. That is, the range of 3 observations [as in a range chart] can be recovered from the pairwise differences [as in the Bland-Altman plots], though not conversely.

In summary, reproducibility is an important criterion for assessing proteomic experiments, and is an essential property of validation. In this regard, range charts provide immediate graphical representation of comparison studies, from which unacceptable or untoward levels of variability can be discerned. Range charts constitute straightforward assessments of method comparison and agreement, and are complementary to more formal assessments of agreement, as described by Bland and Altman, (1999) and Bland and Altman, 2007.

We thank the reviewers for their insightful comments. This research was support in part by grant PO1CA164898 from the National Institutes of Health.