Organic light-emitting diodes (OLEDs) have received considerable interest due to their promising applications in the large-area flat-panel displays and solid-state lighting [1-6]. The devices using organic materials have shown several advantages over their inorganic counterparts, for example, light weight, potentially low cost, capability of thin-film, largearea, and flexible device fabrication, and wide selection of emission colors via molecular design of organic materials. However, the lower efficiency of OLEDs is a thorny obstacle to the application of efficient light-emitting devices. Since the first report on OLEDs in 1987, the light generation efficiencies of OLEDs have been steadily increased by using novel materials and the different device structures [7-9]. Unfortunately, most OLEDs emitters are still not satisfactory. Therefore, the design and synthesize for new emitting materials with high efficiency and thermal stability remain one of the most active areas of the studies. A number of studies demonstrate that the interplay between theory and experiment is capable of providing useful insights into the understanding of the the nature of molecules [10,11]. Among the various kinds of OLEDs materials, 1,8-naphthalimide (NI) derivatives usually exhibit strong fluorescence and good photostability [12-14]. They have been widely used as the most important materials for fabrication of OLEDs. Furthermore, NI derivatives have high electron affinity and excellent transport property due to the existence of an electron-deficient centre. Thus, NI derivatives have been extensively applied in many fields such as coloration and brightening of polymers [15], potential photosensitive biologically units [16], fluorescent markers in biology [17], light emitting diodes [18,19], fluorescence sensors and switchers [20], and electroluminescent materials , and electroluminescent materials [21]. A large variety of auxochromic groups in NI derivatives may be easily grafted to fine tune the absorption and emission wavelengths. Naphthalimides comprise a class of fluorophore whose electronic absorption and emission depend upon the properties of the surrounding medium. The emission spectrum can be tuned by introducing different electron-donating substituent groups, such as N-substituted groups [22], C-substituted groups [23], and O-substituted groups [24]. Furthermore, substitution of electrondonating groups usually increases the intensity of the fluorescence emission, particularly when a methoxy or amino group at C-4 position is used. Recently, some starburst amorphous molecules 1,3,5-Tris(1,8- naphthalimide-4-yl)benzenes have been reported [25]. It was found that the devices using these molecules performance are better than using the most prevalent tris(8-quinolinato)aluminum (Alq3) as a counterpart.

With the above considerations, in this work, we investigated a series of star-shaped molecules with benzene as core and NI derivatives as end groups for OLEDs applications (Scheme 1). An in-depth interpretation of the optical and electronic properties of these compounds has been presented. Several derivatives (1–6), as shown in Scheme 1, have been designed to provide a demonstration for the rational design of novel luminescent and charge transporting materials for OLEDs (Scheme 1).

Scheme 1: Geometries of Designed Molecules 1–6.

All calculations have been performed using Gaussian 09 code [26]. Generally, the B3LYP method appeared notably adapted to NI derivatives [27-31]. Therefore, The geometry optimization of designed molecules in ground states (S0) were carried out by the B3LYP method using the 6-31G(d,p) basis set. The corresponding geometry in the first excited singlet state (S1) were optimized using the TD-B3LYP with 6-31G (d,p) basis set. The harmonic vibrational frequency calculations using the same methods as for the geometry optimizations were used to ascertain the presence of a local minimum. The absorption and fluorescent properties of 1–6 have been predicted using the TD-B3LYP/6-31G(d,p) method based on the S0 and S1 optimized geometries, respectively. To investigate the influence of solvents on the optical properties for the S0 and S1 states of the molecular systems in chloroform (dielectric constant: 2.0906) solvent, we performed the polarized continuum model (PCM) [32] calculations at the TD-DFT level.

The stability is a useful criterion to evaluate the nature of devices for charge transport and luminescent materials. To predict the stability of 1–6 from a viewpoint of conceptual density functional theory, the absolute hardness, η, of 1–6 were calculated using operational definitions [33,34] given by:

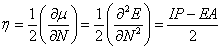        (1)

Where, μ is the chemical potential and N is the total electron number. In this work, the values for IP (ionization potential) and EA (electron affinity) were determined according to the equation IP = E_cr - E_p and EA = E_p - E_ar, where p, cr, and ar indicate the parent molecule and the corresponding cation and anion radical generated after electron transfer.

Frontier molecular orbitals

To characterize the optical transitions and the abilities of electron and hole transport, it is useful to examine the frontier molecular orbitals (FMOs) of the compounds under investigation. The origin of the geometric difference introduced by excitation can be explained, at least in qualitative terms, by analyzing the change in the bonding character of the orbitals involved in the electronic transition for each pair of bonded atoms. An electronic excitation results in some electron density redistribution that affects the molecular geometry [35]. We calculated the distribution patterns of FMOs for 1–6 in S₀ (Figure 1). The total and partial densities of states (TDOS and PDOS) on each fragment of the investigated molecules around the HOMO – LUMO gaps were calculated based on the current level of theory. The FMOs energies EHOMO and ELUMO, HOMO – LUMO gaps, and the contributions of individual fragments (in %) to the FMOs of 1–6 are given in Table 1. As shown in Figure 1, the S₀ → S₁ excitation process can be mainly assigned to the HOMOs → LUMOs and HOMOs-1 → LUMOs transitions, which correspond to a π–π* excited singlet state. For 1, 2, and 5, the HOMOs are distributed on the 1,8-naphthalimide (NI) and benzene (BZ) moieties, with minor contributions from N-substituent groups (SG). The sum contributions of NI and BZ fragments of HOMOs are larger than 97.2%, while the corresponding contributions of SG fragments are within 2.8%, respectively. For 3 and 6, the HOMOs are mainly localized on the SG fragments with only minor contributions from NI and BZ fragments. The contributions of SG fragments of HOMOs are larger than 95%, while the corresponding sum contributions of NI and BZ fragments are within 4.9%, respectively. For 4, the HOMOs are distributed on the NI and SG fragments, with minor contributions from BZ fragment. However, the LUMOs of 1–6 are mainly composed of contributions of NI, with minor contributions from SG and BZ fragments. The contributions of NI fragments of LUMOs are larger than 92.6%, while the corresponding sum contributions of SG and BZ fragments are within 7.4%, respectively.

Figure 1:Electronic density contours of the frontier molecular orbitals for investigated derivatives.

The distribution patterns of the FMOs also provide a remarkable signature for the charge-transfer character of the vertical S₀ → S₁ transition. Analysis of the FMOs indicates that the excitation of the electron from the HOMO to LUMO leads the electronic density to flow mainly from the SG and BZ fragments to NI fragments for 1, 2, 4, and 5. The percentages of charge transfer are the differences between the contributions of fragments for LUMOs and the corresponding contributions for HOMOs in the compounds under investigation. The percentages of charge transfer from SG and BZ fragments to NI fragments are 7.2, 8.2, 39.2, and 9.1%, respectively. On the contrary, for 3 and 6, the excitation of the electron from the HOMO to LUMO leads the electronic density to flow mainly from SG fragments to BZ and NI fragments. The percentage of charge transfer of 3 and 6 are 95.1 and 98.1%, respectively.

Another way to understand the influence of the optical and electronic properties is to analyze the E_HOMO, E_LUMO, and E_g values. From Table 1, one can find that the E_HOMO values of 2, 4, and 5 decreases, while the corresponding value of 3 and 6 increase compared with that of 1. The HOMOs energies are in the order of 3 > 6 > 1 ≈ 2 > 5 4. However, the values of ELUMO and HOMO–LUMO gaps Eg for 2–6 decrease compared with those of 1. The sequence of LUMOs energies is 1 ≈ 2 ≈ 5 > 3 6 > 4. The Eg values are in the order of 1 ≈ 2 ≈ 5 > 4 3 > 6. It implies that the introduction of different donor groups to the 1 leads to the change of the E_HOMO, E_LUMO, and Eg values for its derivatives. The absorption and fluorescence spectra can be tuned by donor groups, providing a powerful strategy for prediction of the optical properties of novel electroluminophores.

Absorption and Fluorescence Spectra

The absorption λ_abs and fluorescence λ_fl wavelengths, main assignments, and the oscillator strength f for the most relevant singlet excited states in each molecule are listed in Tables 2 and 3, respectively. The λ_abs and λ_fl values of 1 are all in agreement with experimental results [25], the deviations are 5 and 25 nm, respectively. The Stokes shift of 1 is 36 nm, which is comparable to the experimental 66 nm. Thus, this result credits to the computational approach, so appropriate electronic transition energies can be predicted at these levels for this kind of system.

For the absorption spectra, the excitation to the S1 state corresponds mainly to the HOMO-1 → LUMO for 1, while the corresponding excitations for 2–6 correspond mainly to the HOMOs → LUMOs and HOMOs → LUMOs+1 and/or HOMOs → LUMOs + 2. From Table 2, one can find that the λabs values of 1–6 are almost equal to that of 1. It suggests that the substituent effects do not significantly affect the absorption spectra of 2–6 compared with those of 1. Moreover, 2–6 have nearly equal values of oscillator strengths, being smaller slightly than the value of 1. The oscillator strength for an electronic transition is proportional to the transition moment [36]. In general, larger oscillator strength corresponds to larger experimental absorption coefficient or stronger fluorescence intensity. This implies that these bipolar molecules shown large absorption intensity.

For the fluorescence spectra, the HOMO ← LUMO+1 and HOMO- 1 ← LUMO excitations play a dominant role for 1. The fluorescence peaks of 2, 3, and 5 are mainly correspond to HOMOs-1 ← LUMOs excitations. The λfl value of 2 is almost equal to that of 1, while the λfl values of 3–6 show bathochromic shifts 5, 27, 8, and 53 nm compared with that of 1, respectively. The Stokes shifts of 3–6 are 41, 58, 44, and 86 nm, respectively. Furthermore, the f values 2–6 are almost equal to that of MEBN, corresponding to strong fluorescence spectra. This implies that 2–6 have large fluorescent intensity and they are promising luminescent materials for OLEDs. As shown in Table 3, it clearly shows that the substituent groups can affect the fluorescence spectra of these molecules. The emissions color of molecules can be tuned by the N-substituent groups. Furthermore, all the substituted derivatives show stronger fluorescence intensity (Tables 2 and 3).

The charge transfer rate can be described by Marcus theory [37,38] via the following equation:

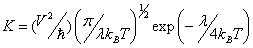               (2)

Where, T is the temperature, k_B is the Boltzmann constant, λ represents the reorganization energy due to geometric relaxation accompanying charge transfer, and V is the electronic coupling matrix element (transfer integral) between the two adjacent species dictated largely by orbital overlap. It is clear that two key parameters are the reorganization energy and electronic coupling matrix element, which have a dominant impact on the charge transfer rate, especially the former.

For the reorganization energy λ, they can be divided into two parts, external reorganization energy (λ_ext) and internal reorganization energy (λ_int). λ_ext represents the effect of polarized medium on charge transfer, which is quite complicated to evaluate at this stage. λ_int is a measure of structural change between ionic and neutral states [39,40]. Our designed molecules are used as charge transport materials for OLEDs in the solid film; the dielectric constant of the medium for the molecules is low. The computed values of the external reorganization energy in pure organic condensed phases are not only small but also are much smaller than their internal counterparts [41,42]. Moreover, there is a clear correlation between λ_int and charge transfer rate in literature [43,44]. Therefore, we mainly study the λ_int of the isolated active organic π-conjugated systems owing to ignoring the environmental changes and relaxation in this work. Hence, the λ_e and λ_h can be defined by equations (3) and (4): [45]

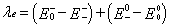            (3)

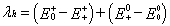              (4)

Where, E₀⁺ ( E₀⁻ ) is the energy of the cation (anion) calculated with the optimized structure of the neutral molecule. Similarly, E₊⁺ ( E₋⁻ ) is the energy of the cation (anion) calculated with the optimized cation (anion) structure, E⁰₊ ( E⁰₋ ) is the energy of the neutral molecule calculated at the cationic (anionic) state. Finally, 00 E is the energy of the neutral molecule in ground state. For comparing with the interested results reported previously [46,47], the reorganization energies for electron (λ_e ) and hole (λ_h) of the molecules were calculated at the B3LYP/6-31G (d,p) level on the basis of the single point energy.

The calculated reorganization energies for hole and electron are listed in Table 4. It is well-known that, the lower the reorganization energy values, the higher the charge transfer rate [37,38]. The results displayed in Table 4 show that the calculated λ_e values of 1–6 (0.110 – 0.180 eV) are larger than that of tris(8-hydroxyquinolinato) aluminum(III) (Alq3) (λ_e = 0.276 eV), a typical electron transport material [46]. It indicates that their electron transfer rates might be higher than that of Alq3, suggesting that 1–6 could be good electron transfer materials from the stand point of the λe values. On the other hand, the calculated λh values of 2–6 (0.292 – 0.328 eV) are larger than that of N,N’-diphenyl-N,N’-bis(3- methylphenyl)-(1,1’-biphenyl)-4,4’- diamine (TPD), which is a typical hole transport material (λ_h = 0.290 eV) [47]. It indicates that their whole transfer rates might be lower than that of TPD. It indicates that 1–6 can be used as promising electron transport materials in OLEDs from the stand point of the smaller reorganization energy.

As the stability is a useful criterion to evaluate the nature of devices for charge transport and luminescent materials. The absolute hardness η is the resistance of the chemical potential to change in the number of electrons. As expected, inspection of Table 4 reveals clearly that the η values of 2–6 are almost equal to that of values of 1. These results reveal that the different π-conjugated bridges do not significantly affect the stability of these bipolar molecules.

In this paper, a series of star-shaped molecules with benzene core and naphthalimides derivatives end groups have been systematically investigated. The FMOs analysis have turned out that the vertical electronic transitions of absorption and emission are characterized as intramolecular charge transfer (ICT). The calculated results show that their optical and electronic properties are affected by their substituent groups in N-position of 1,8-naphthalimide. The study of substituent effects suggest that the λ_abs values of 2–6 are almost equal to that of the parent compound 1, while the λ_fl of 2–6 show bathochromic shifts compared with that of 1. Furthermore, 2–6 have large fluorescent intensity. The different substituent groups do not significantly affect the stability of these molecules. Our results suggest that 2–6 are expected to be promising candidates for luminescent materials and electron transport materials for OLEDs.

Financial support from the Inner Mongolia Key Laboratory of Photoelectric Functional Materials and Natural Science Foundation of Inner Mongolia Autonomous Region (No. 2011ZD02) are gratefully acknowledged.