Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2014) Volume 3, Issue 3
The properties of the historical real exchange rate series constructed in Taylor have been re-examined in this paper. Focusing on two significant sources of bias (structural change and small sample bias), our results do not support for Taylor’s claim that the abrupt changes which occurred throughout the twentieth century (political, economic, institutional, and so on) do not have any effect on the persistence of the real exchange rates. Our results indicate that both the assumption of structural stability and the hypothesis of nominal exchange rate neutrality are violated. The degree of shock persistence shows remarkable heterogeneity between and within monetary regimes. As a consequence, the monetary policymakers’ decisions seem to have a substantial impact on the different reverting dynamics.
<Due to the difficulty of proving the stationarity of the real exchange rates (hereafter RERs) definitively, the tendency has been to extend the sample size in order to increase the power of the tests [1,2] because merely increasing the frequency of observation was not sufficient [3]. Paradoxically, the more bigger the sample, the more important it is to consider structural changes [4]. Empirical exchange rate literature has not paid sufficient attention to the effect which different monetary regimes may have on the stochastic properties of real exchange rates. Furthermore, all the studies which have recently reviewed the general state of the issue [2,5-7] have placed special emphasis on the fact that the conclusions reached have not taken into account the potential effect
With different institutional regimes might have on the behaviour of the RERs. Quite a few studies have used a large time span to analyse the behaviour of the so-called industrialized countries1. Only some of them, however, have studied the stability of the regression parameters. Moreover, when they did so, the evidence was rather mixed. Lothian and Taylor [8], for instance, using a Chow test, did not find different behaviour in the U.S. dollar-British pound and French franc-British pound RERs as a result of the collapse of Bretton Woods. Neither did Lothian and McCharty [9] find evidence of structural change for the case of the Irish pound against the German mark, the British pound and the U.S. dollar as a result of the transition to a floating regime during the seventies. However, the setting up of the European Monetary
System provoked a break in the behaviour of the Irish pound and the German mark. The results of Hegwood and Papell [4] are more promising because the consideration of the parameter instability helps to resolve the ‘purchasing power parity (PPP) puzzle’ [5]. This puzzle refers to the apparent contradiction between the high persistence of RERs found in empirical studies2 and the strong variability of these in a world where financial and monetary shocks are predominant. Hegwood and Papell [4] introduced a substantial innovation into the analysis of RER behaviour: the endogenous detection of break dates. Re-examining the data set of Lothian and Taylor [8] allowed them to discover permanent shocks. It also led them to coin the concept of ‘quasi purchasing power parity’: RERs are still mean reverting (return quickly to their long-run equilibrium after a shock) but the equilibrium value is altered as a consequence of a few shocks whose effects do not dissipate over the time. However, the break points found by Hegwood and Papell [4] did not follow an identifiable common international pattern. They seem to be explained by autochthonous factors, supporting the nominal exchange rate neutrality hypothesis.
Nevertheless, some economists suppose that the stochastic properties of the RERs are conditioned by the nature of monetary regimes [10-12]. In particular, the variability of nominal and real exchange rates are persistently higher under floating nominal exchange rate regimes than under fixed regimes. Mussa [10] for instance, quantified this difference as eight to eighty times greater by using data of thirteen industrialized countries versus the United States over the post-war period. On the contrary, Grilli and Kaminski [13] claim that these differences were due to the specific historical periods rather than to institutional agreements. Similarly, Pozo [14] analysing the real exchange rate of the British pound relative to the U.S. dollar over the period 1900-1940, found that, if the explosion of RER volatility at the start of floating regimes is removed, the volatility seems to be the same in fixed and floating exchange rate regimes.
Frankel and Rose [15] highlight that not only can the volatility of the RERs change across nominal rate regimes but also the speed of convergence to equilibrium after a shock. Previously, Caporale et al. [16] studying the Persistence of several real macroeconomic variables, including exchange rates, showed that a shock Disappears markedly more slowly during floating exchange regimes than during fixed ones. That is, the same outcome that Mussa [10] had highlighted for nominal and real exchange rates. Sarno and Valente [17], on the contrary, have recently demonstrated that nominal exchange rates are primarily responsible for restoring the equilibrium under floating regimes. Additionally, it is allegedly for this reason that the persistence of RERs is shorter. Nominal exchange rates absorb the effect of shocks. On the contrary, relative prices are the main drivers of the process of adjustment during fixed nominal exchange regimes and, as a result, a higher persistence of shocks for RERs is reported.
We re-examine the conclusions reached by Taylor [1], for whom institutional agreements have not had any effect on RER persistence. The contributions of our paper are threefold. Firstly, in a univariate framework, the structural stability hypothesis is assessed using the method proposed by Bai and Perron [18,19]. Hegwood and Papell [4] provided evidence of the great significance of this issue in RER analysis. However, their reasoning is based on the assumption that the speed at which shocks die out is the same in the resulting regimes. That is, only the long-run equilibrium value to which the RERs revert changes. When both the equilibrium and the speed of convergence of RERs to this equilibrium value are allowed to change, the estimated break dates suggest a common international pattern of behaviour in RERs. We find that the abandonment of the Classical Gold Standard, once the First World War ended, and the collapse of the Bretton Woods system are shocks that clearly disturb the RER dynamics. Secondly, this latent common pattern is analysed within a multivariate framework. The central aim is to estimate these shocks more precisely [20,21]. We find that the best model to capture the RER behaviour is one that allows four exchange rate regimes. Furthermore, the resulting regimes seem to match the well-known international monetary regimes. Therefore, nominal exchange rate regimes are important in determining RER behaviour. Thirdly, one of the pricing puzzles [22], the PPP puzzle, is addressed. Structural change and small sample bias are both considered when the RER persistence is analysed. Even though our results clash with the PPP puzzle, perhaps because of the restrictions of our model (linearity), they reveal some outstanding ideas. One, a great heterogeneity in RER persistence between and within regimes is discovered. Two, unexpectedly, the persistence of the RERs during the Bretton Woods period, a seemingly stable regime, is the most heterogeneous. Moreover, this regime is the most persistent. Three, only the persistence over the interwar period can be explained, for example, by sticky price macroeconomic models which predict a half-life of between 1 and 2 years. And four, although the relationship between nominal regimes and the persistence of RERs is unclear in the empirical literature [10,16,17], a substantial –and general– increase in RER persistence is found when we switch from the interwar regime, with broadly floating rates, to the Bretton Woods parities system.
The rest of the paper is organized as follows. In Section 2 the data set is presented. The existence of structural changes is analysed in Section 3 in two complementary frameworks: equation by equation and setting a system of equations. Econometric methods and empirical results are also discussed. Section 4 takes the previous results into account to study the persistence of RERs. Finally, the conclusions are presented in Section 5.
Data
The data set is obtained from the seminal paper of Taylor [1]. This paper is certainly helpful since it considers a great deal of information about the evolution of the nominal exchange rates and some price indexes for a broad sample of countries over an extensive period. RERs are constructed for 17 countries: Argentina, Australia, Belgium, Canada, Denmark, Finland, France, Germany, Italy, Mexico, the Netherlands, Norway, Portugal, Spain, Sweden, Switzerland and the United Kingdom, using the consumer price deflators. Therefore, the sample is mostly composed of the so-called industrialized countries, although it also includes two Latin American countries. All variables were US consumer price deflator at t . Accordingly, the U.S. dollar is taken as the numeraire currency. Annual data from 1870 to 1996 is used in the sample although we do not have a balanced panel at our disposal before 1892 (Table 1).
| WD max | Break date estimates TBj | |||||||
|---|---|---|---|---|---|---|---|---|
| α = 0.05 | [95% confidence intervals] | |||||||
| RER | Sample | p | UD max | α = 0.01 | j = 1 | j = 2 | j = 3 | j = 4 |
| Argentina | 1884-1996 | 2 | 8.879 | 16.639** | 1974 | |||
| 18.614 | [1934-1983] | |||||||
| Australia | 1870-1996 | 1 | 13.517** | 13.517** | 1916 | |||
| 13.517 | [1880-1919] | |||||||
| Belgium | 1880-1996 | 1 | 68.202*** | 80.233** | 1918 | 1935 | ||
| 86.277*** | [1916-1919] | [1933-1937] | ||||||
| Canada | 1870-1996 | 1 | 9.765 | 15.510** | 1976 | |||
| 17.276*** | [1957-1983] | |||||||
| Denmark | 1880-1996 | 1 | 20.416*** | 24.018** | 1970 | |||
| 25.827*** | [1957-1978] | |||||||
| Finland | 1881-1996 | 1 | 68.761*** | 68.761** | 1901 | 1918 | 1939 | |
| 68.761*** | [1897-1902] | [1916-1920] | [1929-1946] | |||||
| France | 1880-1996 | 2 | 19.355*** | 19.355** | 1927 | |||
| 20.755*** | [1906-1933] | |||||||
| Germany | 1880-1996 | 3 | 10.388 | 12.213 | ||||
| 12.884 | ||||||||
| Italy | 1880-1996 | 2 | 25.177*** | 32.761** | 1920 | 1945 | 1962 | |
| 36.125*** | [1918-1925] | [1958-1967] | [1942-1948] | |||||
| Mexico | 1886-1996 | 1 | 12.014** | 23.555** | 1918 | 1980 | ||
| 26.378*** | [1894-1925] | [1935-1983] | ||||||
| Netherlands | 1870-1996 | 1 | 13.541** | 15.930** | 1970 | |||
| 17.130*** | [1937-1974] | |||||||
| Norway | 1870-1996 | 2 | 29.503*** | 29.503** | 1918 | 1947 # | 1969 | |
| 29.503*** | [1910-1922] | [1920-1977] | [1966-1974] | |||||
| Portugal | 1890-1996 | 1 | 15.481*** | 24.697** | 1920 | |||
| 27.509*** | [1917-1950] | |||||||
| Spain | 1880-1996 | 2 | 22.298*** | 34.445** | 1901 | 1918 | 1948 | 1970 |
| 38.557*** | [1898-1908] | [1913-1919] | [1943-1950] | [1967-1973] | ||||
| Sweden | 1880-1996 | 1 | 28.426*** | 28.426** | 1918 | 1935 | ||
| 28.751*** | [1913-1920] | [1926-1945] | ||||||
| Switzerland | 1892-1996 | 2 | 15.870** | 22.360** | 1914 | 1972 | ||
| 25.014*** | [1897-1918] | [1964-1973] | ||||||
| United Kingdom | 1870-1996 | 1 | 13.119** | 18.667** | 1918 # | 1948 | 1976 | |
| 20.792*** | [1895-1923] | [1944-1950] | [1969-1979] | |||||
NOTES: Estimate results for Model (1). p is chosen by a specific-to-general approach (see text). UDmax and WDmax test statistics are computed imposing an upper bound
M = 5 for m and a trimming parameter of 0.15.
*, **, *** Indicate statistical significance at the 10, 5 and 1% levels, respectively.
# Denotes a significant break date at the 10% level.
Table 1: Break date estimates using the Bai and Perron procedure.
Structural change
There are many factors, of all kinds, which may disrupt the dynamics of economic variables and it would be unwise to ignore them. Furthermore, once the importance of these factors has been admitted, one should be generous and let the time series data themselves discover the best model to capture their presence. Studying a significant number of macroeconomic time series, representative of the post-war U.S. economy, Stock and Watson [23] reached the conclusion that the parameter stability assumption did not seem warranted. The same was true, and even more so, for times series related to prices indexes. In a similar manner, Clarida et al. [24] underlined that the monetary policy adopted by the Federal Reserve from 1979 may have changed the U.S. macroeconomic behaviour.
The purpose of this section is to assess the instability hypothesis of RER behaviour only focusing on the model parameter stability or its absence, discerning whether the behaviour of RERs has remained safe from the brusque institutional, political and economic changes which have taken place throughout the twentieth century. This work has been carried out using two complementary approaches but always within a linear framework: equation by equation and setting a system of equations.
Univariate analysis
Instability tests: A methodology which consistently estimates the unknown break points together with the remainder of the model parameters is proposed by Bai and Perron [18,19].
The dynamics of the RERs are expressed as follows:
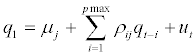 (1)
(1)
For 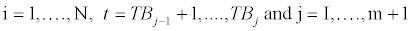 m co-breaks are allowed which occur at the unknown points (TB1,…..TBm) and the convention TB0 =0 and TBm+1 =T. Equation (1) is a simple autoregressive model of order p where both order the regression coefficients that control the persistence of the RERs and the regression coefficient that controls the mean of the process are regime-dependent3. It is what is known as a pure structural change model in this strand of literature. In the specific case of RERs, a first order autoregressive process is enough to capture their evolution, at least, when working with yearly data [25,26]. Nevertheless, a higher order is allowed to avoid serially correlated errors which would mean that the AR 1 model is inadequate. Likewise, changes in the variance of the errors are allowed but, since the parameter estimation method is based on the least squares principle, these changes, if there are any, must occur at the same point as the remainder of the model parameters [27]. Lastly, it is important to impose a large trimming parameter. In other words, a minimum length of the regimes
m co-breaks are allowed which occur at the unknown points (TB1,…..TBm) and the convention TB0 =0 and TBm+1 =T. Equation (1) is a simple autoregressive model of order p where both order the regression coefficients that control the persistence of the RERs and the regression coefficient that controls the mean of the process are regime-dependent3. It is what is known as a pure structural change model in this strand of literature. In the specific case of RERs, a first order autoregressive process is enough to capture their evolution, at least, when working with yearly data [25,26]. Nevertheless, a higher order is allowed to avoid serially correlated errors which would mean that the AR 1 model is inadequate. Likewise, changes in the variance of the errors are allowed but, since the parameter estimation method is based on the least squares principle, these changes, if there are any, must occur at the same point as the remainder of the model parameters [27]. Lastly, it is important to impose a large trimming parameter. In other words, a minimum length of the regimes 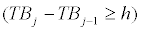 has to be imposed because regimes which are too short might produce imprecise parameter estimates and tests with substantial size distortions4 [18].
has to be imposed because regimes which are too short might produce imprecise parameter estimates and tests with substantial size distortions4 [18].
Furthermore, notice that, in Model (1), the presence of a deterministic time trend is not allowed. Although Cuddington and Liang [28] and Lothian and Taylor [29] started the interesting debate of the inclusion of deterministic trends in RER specifications, these have not been here considered for two reasons. The main one is related to the Cassellian version of the PPP theory [30,31], RERs are not continually at their PPP level because there are some factors that make this impossible, but disturbances disappear in a reasonably short time.
In the long run, however, RERs should revert to a constant mean and not to a constant time trend. International arbitrage is the mechanism that causes international prices to be equalized and, therefore, restores the stable equilibrium level of RERs. The second reason, no less powerful than the first, is that the presence of trending regressors is precluded in the Bai and Perron [18,19] methodology.
The Bai-Perron procedure implies the estimation of Model (1) considering that the break may appear in any period of the sample. A Chow-type test is then defined in order to determine the existence of a first break, which coincides with the period where this Chowtype statistic reaches its maximum value. The existence of multiple breaks is analyzed by applying this procedure sequentially, combining with the repartition method described in Bai [32]. To prove evidence supporting the structural change hypothesis, we use the double maximum test statistics, which test for the null hypothesis of no structural breaks against the alternative of the presence of an unknown number of breaks, given some upper bound M for the possible number of breaks m. Once we can offer evidence against the absence of breaks, we can then apply a sequential procedure in order to determine the most appropriate number of breaks. This approach is based on the sequential application of the 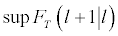 statistic starting with a value of l equal to one. The
statistic starting with a value of l equal to one. The 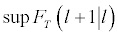 statistic is defined as the difference between the sum of squared residuals obtained with l breaks and that obtained with (l+1) breaks. The l+1 break point estimation
statistic is defined as the difference between the sum of squared residuals obtained with l breaks and that obtained with (l+1) breaks. The l+1 break point estimation 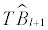 does not need to have been obtained from a global minimization of the sum of squared residuals; a partial minimization is sufficient. Bai and Perron [19] noticed that pursuing a different strategy makes it difficult to obtain the asymptotic distributions of the test statistics (see Bai [20] who follows a different approach).
does not need to have been obtained from a global minimization of the sum of squared residuals; a partial minimization is sufficient. Bai and Perron [19] noticed that pursuing a different strategy makes it difficult to obtain the asymptotic distributions of the test statistics (see Bai [20] who follows a different approach).
RER instability
Table 1 summarizes the results of applying the Bai-Perron procedure. However, before implementing it, we must ensure that the RER series do not exhibit a unit root or, in other words, we must find significant evidence of stationarity. Otherwise, hypothesis tests based on asymptotic theory might be misleading. Taylor [1], whence the data set has been taken, has emphasized that it is not more productive to devote more effort to the RER stationarity inquiry since the PPP has held in the long run throughout the twentieth century. We assume that Taylor’s outcomes are correct although this topic remains a thorny issue (see, for instance, Lopez et al. [33] and Papell and Prodan [31]) 5.
A specific-to-general approach is pursued to choose the order p of the autoregressive model. The idea is to test the entire sample for no serial correlation in the errors using the Ljung-Box portmanteau test. The process starts by specifying an AR 1 model and increasing the order p iteratively until the null hypothesis of serially independent errors cannot be rejected. The value of p chosen is how many times the null hypothesis is rejected plus one. As Table 1 highlights a first-order autoregressive model is generally sufficient to capture the behavior of the RERs. However, Argentina, France, Germany, Italy, Norway, Spain and Switzerland have required a higher order.
The statistical significance of the double maximum tests reported in Table 1 indicates that the parameter stability hypothesis only holds for the case of Germany. Consequently, the remaining 16 RERs show strong evidence of structural change. The most straightforward explanation that comes to mind for this exception is the fact that the German RER has needed an autoregressive order higher than two in this specification. Moreover, the number of structural changes determined by the Bai-Perron procedure differs substantially between RERs. In some of them, a single break date is chosen but the majority needs a model with at least two breaks. For instance, four changes are detected in Spain and three in Finland, Italy, Norway and the United Kingdom, although, in the last two, the third break is only statistically significant at the 10 percent level.
However, even though the rejection of the hypothesis of parameter stability is undoubtedly important, the most striking result derived from Table 1 is related to the question of the neutrality of nominal exchange rate regime [16,17,22]. That is, Table 1 shows that the breaks are located at two specific points of time which are constantly repeated: 1918 and a year close to 1970. When we consider the confidence intervals of the estimated break dates, 12 of the 16 RERs in which structural change has been detected contain the first estimated break date and 10 RERs have the second date.
Therefore, both the abandonment of the Classical Gold Standard, once the First World War ended, and the collapse of the Bretton Woods parities system have apparently shaped the dynamics of RERs over the twentieth Century. This result significantly contradicts the conclusions reached by Hegwood and Papell [4] who claim that the change points are due to country-specific features (economic, political) and not to major international Agreements. Lastly, notice also that there is another break date for a few countries in the second half of the 1930’s or 1940’s. Moreover, the Spanish and Finnish RERs display an additional estimated break date in the Classical Gold Standard when it was set in motion effectively. Paradoxically, the Spanish peseta, a peripheral currency, never adhered to this great institutional agreement [34].
To sum up, individual RER evidence suggests an average of at least two structural break dates in the twentieth century. Furthermore, the estimated break dates seem to draw an international common pattern of behaviour in the RERs. Nevertheless, this apparent regimentdependence has not always been supported by the empirical literature. The analysis carried out in [1] involves the separation of RER evolution into different monetary regimes. Even though the resulting exchange rate regimes are closely linked to very well known historical episodes, we consider it more appropriate to determine these periods without imposing any a priori restriction, obtaining this information directly from the time series data by way of the application of powerful econometric techniques to detect and estimate the presence of structural breaks. The next section is devoted to assessing the validity of this potential common international pattern of behaviour.
System of equations: co-evolution
Heretofore we have addressed the dynamics of the RERs in an individual way: equation by equation. In this sub-section, an analogous analysis is carried out but more information is added to the initial model. Since all the RERs exist in a common international environment and the decisions of economic policy taken by different national governments are strongly interrelated, all RERs should be exposed to the same shocks. That is why a model that takes into account the contemporaneously correlated disturbances between equations can provide a more accurate depiction of RER behaviour. Likewise, it may shed more light on the shocks that are really important in the dynamics of RERs. Of course, these shocks substantially alter the stochastic properties of the RERs, but these properties will be discussed later on.
So, we employ a Seemingly Unrelated Regression (SUR) model. As before, the linear property is maintained. The estimation method is basically a least squares estimator with a special covariance matrix. To be exact, it is a Feasible Generalized Least Squares (FGLS) estimation: the so-called SUR estimation [35]. The purpose of using a multivariate regression model is widely known: there is a significant efficiency gain in the parameter estimation when information from different equations is combined, which we shall try to make good use of for estimating cobreak points6.
The empirical results of the structural change analysis in an individual framework seem to provide fairly clear evidence of a de facto international common pattern, namely, a set of shocks which no country is able avoid and whose effects persist in RER behavior. Again, the purpose of this sub-section is to estimate break points but now in the context of a system of equations: locating co-break dates.
Tests
To study whether there is a unique common international pattern in RER behaviour, the following system of equations is considered in which co-breaks are modeled using dummy variables:
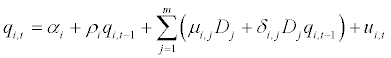 (2)
(2)
where the number of equations i =1,…,17 and the data span the period t=1892,…,1996 . Dj is a dummy variable that takes the value 1 when t>TBjand the value 0, otherwise. TBj denotes the time where the j co-break point appears (j=1,…,m) and m denotes the number of co-breaks, both of which are treated as unknown. Note that a modified AR(1) model with m+1 regimes is considered, that is, as above, a pure structural change model7. Model (2) is estimated by the iterated FGLS method, which is equivalent to the maximum likelihood estimation [36]
A Likelihood Ratio (LR) statistic for testing the null hypothesis of m co-breaks against the alternative hypothesis of m+1 co-break is defined as:
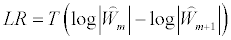 (3)
(3)
where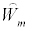 and
and 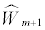 are the residual sums of squares and cross-product matrices in a model with m and m+1 co-breaks, respectively. T denotes the number of available observations. The LR statistic is asymptotically distributed under the null hypothesis as a chi-square with as many degrees of freedom as the number of restrictions imposed. Instead of using chi-square critical values, in view of the fact that they could be inappropriate [37] a parametric bootstrap distribution is computed assuming, when the pseudo-samples are generated, that the p initial values are known (see Table 2); p being the autoregressive process order.
are the residual sums of squares and cross-product matrices in a model with m and m+1 co-breaks, respectively. T denotes the number of available observations. The LR statistic is asymptotically distributed under the null hypothesis as a chi-square with as many degrees of freedom as the number of restrictions imposed. Instead of using chi-square critical values, in view of the fact that they could be inappropriate [37] a parametric bootstrap distribution is computed assuming, when the pseudo-samples are generated, that the p initial values are known (see Table 2); p being the autoregressive process order.
| Test | Null hypothesis / alternative | LR Statistic | Co-break date estimates 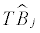 |
|||
|---|---|---|---|---|---|---|
| j=1 | j=2 | j=3 | j=4 | |||
| I | 0 Co-breaks/1 Co-Break | 132,3*** | 1918 | |||
| II | 1 Co-Break at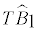 / 2 Co-Breaks / 2 Co-Breaks |
227,7*** | 1939 | |||
| III | 2 at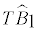 , ,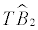 / 3 Co-Breaks / 3 Co-Breaks |
110,3*** | 1976 | |||
| IV | 3 at,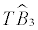 , / 4 Co- Breaks , / 4 Co- Breaks |
81,6 | 1954 | |||
Notes: *** Denotes significance at 1% level.
LR is the Likelihood Ratio test statistic defined in (3).
2,000 pseudo-samples are generated under the null hypothesis following model (2) by the iterated FGLS method through a parametric bootstrap (assuming p initial values
as known). Due to the special nature of the Finnish RER during the first regime, these pseudo-subsamples are not generated.
Bootstrap critical values are the following: Test I: 76,0 and 88,8; Test II: 70,4 and 80,8; Test III: 77,8 and 89,8; Test IV: 81,8 and 99,4 for the significance levels of 5 and
1%, respectively.
Table 2: Estimate results for a system of AR (1) SUR equations.
To estimate the points and the number of co-breaks, a sequential test procedure is proposed. This method, similar to others proposed in the literature, is not intensive computationally. The procedure is based on locating the dominant co-break point conditional on the previously estimated co-break(s). That is, the co-break point at which the greatest reduction in the determinant of the residual covariance matrix is achieved. So,
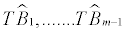 given the previously estimated co-breaks
given the previously estimated co-breaks 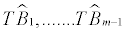 and the imposition of
and the imposition of 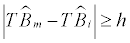 for i=0,1,…… ,m-1, m+1 with
for i=0,1,…… ,m-1, m+1 with 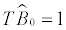 =1and
=1and 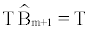 = T 8. The procedure starts with m=0 and increases iteratively until the LR test statistic can not reject the null hypothesis of m co-breaks. Consequently, the estimation of the number of co-break points is how many times the null is rejected. As can be seen, the method is not at all sophisticated; it is just based on testing whether the estimation of an additional co-break point is statistically significant.
= T 8. The procedure starts with m=0 and increases iteratively until the LR test statistic can not reject the null hypothesis of m co-breaks. Consequently, the estimation of the number of co-break points is how many times the null is rejected. As can be seen, the method is not at all sophisticated; it is just based on testing whether the estimation of an additional co-break point is statistically significant.
Real exchange rates: co-break dates
The outcomes of applying this procedure are displayed in Table 2. The first dominant co-break is located in 1918 and, in accordance with the LR test statistic, is significant at the 1 percent level since 132.3 is plainly higher than the parametric bootstrap critical value. It is worth noting that the twelve RERs that show evidence of structural change locate the break point in this year (Table 1). From this table, one would expect the second co-break date to be located in the 1970’s. Surprisingly, once this first co-break point is fixed, the second dominant co-break is located in 1939. This date yields the greatest reduction of the determinant of the residual covariance matrix. The LR test statistic is again significant at the conventional level which is evidence of the existence of a model with at least two co-breaks. The next step consists of testing the null hypothesis of two co-breaks in 1918 and 1939 against the alternative of an additional co-break point. The determinant of the residual covariance matrix attains its minimum value in 1976. This new co-break date is once again statistically significant since the LR statistic is visibly higher than 77.8. The final test (test IV) shows that dummy variables which incorporate a fourth change point into the model are insignificantly different from zero. So, the evidence does not support the existence of a fourth co-break.
Thus, the model that best describes the RER time series is that which allows three co-breaks, in other words, one that admits four exchange rate regimes. The resulting regimes fit nicely into the well known monetary regimes. The first 27 years of the sample (1892-1918) make up the first regime and coincide with the Classical Gold Standard. The second regime is slightly shorter, covering the period 1919- 1939. It corresponds to the interwar period. It is a regime subjected to the flexibility of exchange rates as well as an attempt to regain the credibility and the stability that existed under the Classical Gold Standard [38]. The third regime (1940-1976) mainly includes World War II and the years during which exchange rates are determined by the Bretton Woods system. Finally, the collapse of the Bretton Woods system establishes the beginning of an additional exchange rate regime, the fourth and last, which extends from 1977 to 1996.
Robustness of the results
In this subdivision, the robustness of the results described above is examined. There seem to be two vulnerable premises in our analysis. Firstly, the econometric method with which the co-break dates are determined. The sequential (one-by-one) estimation approach may condition the estimation of co-break dates. Bai [39], for instance, proposed a simple iterative refinement procedure when m=2 with the advantage that the asymptotic factors that hinder the comparison between these two groups. The data set is now modified in order to solve these weaknesses. Only the 16 industrialized countries are considered here. Moreover, the sample length is cover the period 1881 to 2008 (see Appendix for additional details). Likewise, the dummy variables are removed from the specification of the system of AR p SUR equations:
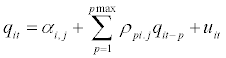 (4)
(4)
For i=1,…..,N, For i=1,…..,N,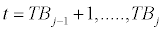 and j=1,….,m+1. M co-breaks are allowed which occur at the unknown points ( ) 1,....., m TB TB and the convention TB0=0 and TB m +1 = T is used. Pmax=2, that is, the auto aggressive order is the same for the whole system and all the regimes. The model is again estimated by the iterated FGLS method.
and j=1,….,m+1. M co-breaks are allowed which occur at the unknown points ( ) 1,....., m TB TB and the convention TB0=0 and TB m +1 = T is used. Pmax=2, that is, the auto aggressive order is the same for the whole system and all the regimes. The model is again estimated by the iterated FGLS method.
A simultaneous approach instead of the sequential method is used9. The procedure is based on estimating the number and the locations of the co-breaks by minimizing the multivariate version of the Schwarz Bayesian information criterion which is defined as:
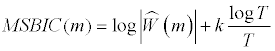 (5)
(5)
Where 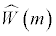 denotes the estimation of the residual covariance matrix in model (4) with m co-breaks, k=N(1+p)(m+1) is the total number of regression coefficients in a system of N equations and T is the number of observations. Explicitly, the estimated number of co-breaks points given an upper bond M for m is
denotes the estimation of the residual covariance matrix in model (4) with m co-breaks, k=N(1+p)(m+1) is the total number of regression coefficients in a system of N equations and T is the number of observations. Explicitly, the estimated number of co-breaks points given an upper bond M for m is 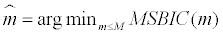 Because, in the univariate analysis described above, the maximum estimated number of breaks chosen was four, an upper bound M=4 is imposed.
Because, in the univariate analysis described above, the maximum estimated number of breaks chosen was four, an upper bound M=4 is imposed.
Table 3 shows that the number of estimated co-breaks under this approach is two, regardless of whether a system of AR 1 equations or a system of AR 2 equations is considered10. Moreover, the estimated co-breaks completely match those previously estimated, which can be interpreted as a sign of the robustness of our empirical results. 1918 and 1939 (1937 in the case of a system of AR 2 equations), once again, are found to be years which decisively disrupt the behaviour of RERs. Unlike the sequential procedure, the simultaneous method only draws three great exchange rate regimes. The extensive regime 1940-2008 is split into two autonomous regimes under the sequential procedure. Even so, from the results in Table 1, it might be excessive to say that this is largely due to the Latin American currency dynamics.
| m | MSBIC | Co-break date estimates TBj | ||||
|---|---|---|---|---|---|---|
| j = 1 | j = 2 | j = 3 | j = 4 | |||
| System of AR(1) SUR equations | ||||||
| 0 | -83.594 | |||||
| 1 | -83.485 | 1922 | ||||
| 2 | -84.160*** | 1918 | 1939 | |||
| 3 | -83.779 | 1918 | 1939 | 1972 | ||
| 4 | -83.096 | 1918 | 1937 | 1956 | 1984 | |
| System of AR(2) SUR equations | ||||||
| 0 | -83.2 | |||||
| 1 | -83.193 | 1919 | ||||
| 2 | -83.991*** | 1918 | 1937 | |||
| 3 | -83.162 | 1918 | 1937 | 1972 | ||
| 4 | -82.128 | 1918 | 1937 | 1956 | 1976 | |
Notes: *** Denotes the model selected under the minimization of the MSBIC criterion.
Table 3: Co-break estimates using the Schwarz information criterion.
Stochastic Properties of Real Exchange Rates: Persistence
Concept and background
In time series analysis, the concept of persistence refers to the dependence between distant time series data. It is said that RER dynamics are persistent since, after a shock, they take a long time to converge to their equilibrium level: their speed of adjustment is extremely slow. The most common scalar measure of persistence in the empirical RER literature is the half-life, a concept adopted from physics, which is defined as the time that a unit shock needs to be permanently reduced to one half. Cheung and Lai [40], nevertheless, noted that the half-lives of shocks may be an imprecise persistence measure. That is why these authors suggest using impulse response analysis for their computation. A large half-life of deviations from equilibrium is associated with the predominance of real shocks, such as technology and tastes. However, RERs, and nominal exchange rates as well, fluctuate extraordinarily in the short term. This high volatility in the time series data may be explained by shocks of a nominal nature, such as monetary and financial shocks which have a transitory effect on the RER behavior. But if RERs oscillate so much in the short term, why do they not return to their long-run equilibrium level more quickly, say one or two years, as nominal wages and prices do in response to the shocks. This issue is what Rogoff [5] has called the ‘PPP puzzle’: the inability of empirical studies to report half-life estimates below an interval of between three and five years.
A number of latent biases, nevertheless, have been underlined in the RER persistence analysis. Quite a few of them greatly increased the degree of scepticism in the interpretation of the RER persistence. Aggregation, either temporal (Taylor, 2001) or cross-sectional [41], non-linearities [1], sample sizes that are too small [42-46,26] or structural instability [4] have, at some moment, been at the centre of the discussion as sources of bias. We are here concerned with the last two, small samples and structural instability, but addressed jointly
It is well known that the inclusion of lagged dependent variables as regresses yields consistent but biased ordinary least squares (OLS) estimates in finite samples. However, it is hard to find a function which relates the bias of the OLS estimates to the parameter values. Analytically there are some approximations. Shaman and Stine (1988) demonstrated the mean-bias of the OLS estimator to order T 1 ; e.g., in a stationary second-order autoregressive model with coefficients 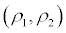 , is
, is 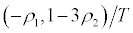 when the mean of the time series process is known and
when the mean of the time series process is known and 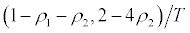 when the mean has to be estimated, where T is the sample size. But the bias function may also be estimated effortlessly through simulation techniques. Following this approach, the mean-bias and median-bias of the estimated coefficients were obtained by Tanizaki [47]. Both mean-bias and median-bias are considerable in small samples although the problem gets even worse as the parameter value 1 approaches unity (the degree of persistence increases) and the number of unnecessary exogenous variables becomes greater, at least, in a first-order autoregressive process.
when the mean has to be estimated, where T is the sample size. But the bias function may also be estimated effortlessly through simulation techniques. Following this approach, the mean-bias and median-bias of the estimated coefficients were obtained by Tanizaki [47]. Both mean-bias and median-bias are considerable in small samples although the problem gets even worse as the parameter value 1 approaches unity (the degree of persistence increases) and the number of unnecessary exogenous variables becomes greater, at least, in a first-order autoregressive process.
Murray and Papell [42,44] mindful of the fact that the measurement of RER persistence used in the empirical research was downwardly biased, employed the exact (and approximate) median unbiased estimation methods proposed by Andrews [48] and Andrews and Chen, [49] to obtain a realistic indicator of the true RER persistence value. This correction, nevertheless, provided even stronger evidence supporting the ‘PPP puzzle’. The point unbiased half-life estimates lay inside the implicit interval of between three and five years pointed out by Rogoff [5] but the upper bounds of the confidence intervals were infinite. That is, they depicted an incomplete picture in which RER shocks died out and the ‘PPP puzzle’ grew in strength. Furthermore, Caporale et al. [46] evidenced that, when obtaining the confidence intervals, the normality assumption in Murray and Papell [42] was relaxed, the estimates of the degree of persistence of deviations from the equilibrium were even higher. Cashin and McDermott [45], however, showed that point and confidence interval estimates of the half-lives, might both be remarkably reduced when median-unbiased estimators that were robust to the presence of heteroskedasticity were utilized. Panel econometric methods, likewise, seemed to be going in the right direction to solve the ‘PPP puzzle’ but, once the small-sample bias was corrected, the results were far from clear. For instance, Murray and Papell [43], in a quarterly panel of 20 countries over the post-Bretton Woods floating period, found that confidence intervals were tighter but still too wide to be consistent with models based on sticky prices. The same results were reported by Choi et al. [26] but several sources of bias were simultaneously corrected.
Lastly, the degree of persistence of macroeconomic time series might be overestimated if potential structural changes are not taken into account [50]. Despite being widely known, this outcome has not been consolidated in the empirical literature of RER persistence. However, as illustrated by Hegwood and Papell [4], the half-life estimates undergo a noteworthy reduction (between 26 and 65 percent) when RERs are allowed to revert to an occasionally changing mean. In the same way, in a non-linear framework, Sarno and Valente [17] found that, when different nominal exchange rate regimes are distinguished, the persistence of RERs is not as puzzling as we had thought.
Method
The aim of the present section is to study the stochastic properties of the RERs over the twentieth century, namely, persistence. As has been noted, several factors might cast doubts on the persistence estimates. Two sources of bias in half-life estimation will be jointly tackled here: structural breaks and small-sample bias11. Both seem to perform in opposite directions, so the final effect on the unbiased estimate of the RER persistence will be uncertain at first glance. The first bias, the structural instability bias, will be removed taking the previous empirical results (Section 3.2.B). That is, once the permanent shocks have been located (the so-called co-breaks above), several exchange rate regimes can be distinguished for which the structural stability hypothesis holds and, consequently, the potential structural instability bias is ruled out. Obviously, dividing the whole sample into different regimes and separately analysing them heightens the smallsample bias. It is known that both the SUR and OLS estimators are seriously downwardly biased in small samples.
However, it is hard to prove analytically which of the two is more unbiased. We continue to rely on the SUR approach under the argument of gaining efficiency.
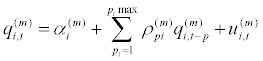 (5)
(5)
where m=1,…,4 denotes the regime under study and t=1892,…..,1914 if m=1; t=1919,…,1939 if m=2, and so on (see Table 2 above for details)12. The lag length Pi is allowed to differ between and within exchange rate regimes. This element is crucial since Model (5) is estimated by the feasible GLS method [35] so coefficients. would be inconsistently estimated if the model was misspecified. Accordingly, pi is chosen, equation by equation, using a general-to-specific criterion with a maximum number of lagged endogenous variables of T 1/ 3. (pi max T 1/ 3). Moreover, a liberal 10 percent is used as the criterion for significance. Finally, notice that, unlike another multivariate studies, e.g., Murray and Papell [43] and Choi et al. [26], cross-sectional persistence heterogeneity is explicitly allowed for in Model (5).
The ‘bootstrap-after-bootstrap’ method of Kilian [51] for the estimation of half-lives is employed through impulse response functions. Kilian’s procedure is based on carrying out a bias-corrected procedure for parameter estimators before running the standard bootstrap. Additionally, a stationarity correction is made to this bias adjustment whenever the initial parameter estimates fail to reject the stationarity assumption. As described by Kilian [51], this stationarity correction merely prevents pushing stationary parameter estimates into the non-stationary region.
The next subsection describes the empirical results of utilizing this procedure.
Empirical results
Table 4 challenges some of the ideas presented in the empirical literature on the persistence of RERs. In the first place, multivariate analysis methods, to be more specific, panel econometric models, show tighter confidence intervals for half-life deviations. For instance, Murray and Papell [43] and Choi et al. [26] both detailed a meanunbiased lower bound of the confidence interval of around 2.5 years over the post-Bretton Woods era and an upper bound of 4 and 5 years, respectively. Nevertheless, these confidence intervals were obtained under the assumption of cross-sectional homogeneity. That is, the persistence across countries in the panel study is identical within the regime under consideration. Undoubtedly, in accordance with Table 4, if it is more reasonable not to reject the assumption of homogeneity in any of the regimes, it should be during the post-Bretton Woods regime (period 1977-1996). In this period, point estimates of half-life deviations from their long-run equilibrium are close to 3 years for most currencies. But notice that the upper bounds estimates of half-lives are markedly different across countries, ranging from 4 years in the case of Portugal to 46 years in Switzerland.
| Regimes | 1892-1914 | 1919-1939 | 1940-1976 | 1977-1996 | ||||
|---|---|---|---|---|---|---|---|---|
| RER | HLMU | 95% CI | HLMU | 95% CI | HLMU | 95% CI | HLMU | 95% CI |
| Argentina | 4.41 | [0.76-7.92] | 1.03 | [0.52-2.45] | 3.51 | [1.15-7.55] | 2.48 | [1.00-6.41] |
| Australia | 3.24 | [0.71-10.70] | 0.64 | [0.40-1.22] | 2.81 | [1.27-4.30] | 3.61 | [1.35-16.41] |
| Belgium | 0.82 | [0.42-14.30] | 4.43 | [1.39-12.30] | 9.38 | [2.51-28.95] | 2.59 | [1.07-4.86] |
| Canada | 3.03 | [0.96-7.09] | 0.97 | [0.49-2.51] | 7.43 | [1.79-14.62] | 3.31 | [0.63-17.64] |
| Denmark | 0.85 | [0.47-1.74] | 1.75 | [0.58-5.31] | 1.88 | [0.92-3.24] | 2.38 | [0.57-9.31] |
| Finland | 1.46 | [0.55-3.28] | 16.31 | [1.80-∞) | 9.74 | [2.37-30.34] | 2.89 | [1.07-6.00] |
| France | 2.33 | [0.62-6.01] | 1.95 | [0.58-6.66] | 8.34 | [3.84-11.63] | 2.95 | [1.29-5.67] |
| Germany | 2.15 | [1.28-2.93] | 3.19 | [1.32-10.16] | 21.27 | [1.43-∞) | 3.2 | [1.20-6.76] |
| Italy | 2.08 | [0.49-∞) | 1.82 | [0.83-3.44] | 16.51 | [2.00-∞) | 3.75 | [1.64-8.22] |
| Mexico | 1.19 | [0.59-1.85] | 1.67 | [0.81-3.04] | 1.9 | [1.32-2.49] | 3 | [1.19-5.99] |
| Netherlands | 1.79 | [0.56-3.90] | 4.75 | [0.71-33.67] | 3.92 | [2.37-5.45] | 3.39 | [1.42-7.00] |
| Norway | 2.2 | [0.80-4.27] | 0.92 | [0.49-2.48] | 6.54 | [1.70-17.28] | 2.46 | [1.10-4.87] |
| Portugal | 1.92 | [0.66-4.30] | 0.93 | [0.50-2.02] | 1.94 | [0.84-3.35] | 2.28 | [1.05-4.03] |
| Spain | 3.7 | [0.69-11.82] | 1.68 | [0.52-5.57] | 1.23 | [0.65-2.46] | 3 | [0.68-18.80] |
| Sweden | 1.78 | [0.83-∞) | 8.18 | [0.78-∞) | 2.03 | [0.84-4.09] | 1.61 | [0.55-7.33] |
| Switzerland | 4.44 | [0.66-20.99] | 0.9 | [0.48-2.58] | 6.14 | [3.40-9.54] | 6.35 | [1.76-46.30] |
| United Kingdom | 6.19 | [0.73-28.05] | 4.52 | [1.36-14.24] | 11.46 | [3.76-35.02] | 2.73 | [0.88-7.45] |
| Median | 2.15 | [0.66-7.09] | 1.75 | [0.58-5.31] | 6.14 | [1.70-9.54] | 2.95 | [1.07-7.00] |
Notes: Mean-unbiased half-life (HLMU) estimates are computed using impulse response analysis following the ‘bootstrap-after-bootstrap’ method proposed by Kilian (1998).
Model (5) is estimated by the SUR methodology and the lag length is determined, equation by equation, according to a ‘general-to-specific’ criterion with a maximum of
lags of T1/3 (10% is chosen as the criterion for significance). 95% confidence intervals (CI) are obtained through bootstrapping with (1000 + 1000 × 1000) replications. The
upper bound estimates of more than 50 years are interpreted as infinite.
Table 4: Mean-unbiased half-life estimates.
On the other hand, the largest heterogeneity is unexpectedly found in the Bretton Woods regime (period 1940-1976) where the point mean-unbiased half-life estimates are between 1.2 years (Spain) and 21.3 years (Germany), with a median of 6.1 years. Some researchers have timidly suggested this heterogeneity as the foundation of a new puzzle [52, 53] and the results summarized here seem to give strong support to this issue. What is more, the outcomes reported in Table 4 reveal that this heterogeneity in the Degree of persistence is not only produced within a specific monetary regime but also commonly emerges across regimes.
Therefore, this underlying heterogeneity in the persistence of RER shocks both between different regimes and within regimes is a puzzle in itself. Ignoring it only introduces a new bias in the half-live estimation. The performance of the fundamental macroeconomic variables behind these persistence patterns probably help to explain this question but it is still an under-researched topic which needs further work to be better understood13.
Secondly, the major conclusions drawn from Table 4 do not support the statement of Taylor [1] when he asserts that the persistence of RERs has remained stable throughout the twentieth century. In fact, each regime, and as previously mentioned, each RER within each regime, shows very disparate properties. Individual RERs return to their long-run equilibrium after a shock at remarkably different speeds of adjustment. The least persistent regime, in which shocks vanish more quickly, is the interwar regime (the period from 1919 to 1939). This is an epoch in which monetary shocks prevailed. Half-life estimates are below two years for two thirds of the examined countries whereas, in the most persistent regime, the Bretton Woods regime, only four countries do so. Even though, during the interwar regime, some unbounded upper bounds of the confidence intervals are found, half of them do not exceed 5.3 years.
Thirdly, some researchers have found an apparent connection between the nominal exchange rate regimes and the degree of the persistence of RERs [10,16,52,9,54,17]. Although the magnitude and the direction of this relationship is not clear, Sarno and Valente [17] unequivocally underlined that fixed nominal exchange rate regimes are more persistent than floating nominal regimes. For instance, a shock of one percent lasts an average of 1.8 years during floating exchange rate regimes, whereas the same shock may take 15 years to die out during a fixed one. Nevertheless, the overall impression of Table 4 does not seem to support this sort of evidence. As just noted, the least persistent regime, namely the interwar period, was a regime of broadly floating nominal exchange rates. But RER shocks during the Gold Standard regime (period 1892-1914), a fixed nominal exchange rate system which operated with firm institutional rules, are less persistent than during the post-Bretton Woods flexible regime. Actually, half-life estimates in the Gold Standard regime are close to those of the interwar regime although the confidence intervals in the latter are slightly narrower. Separately, only a small number of RERs (Argentina, Canada, France, Italy, Norway and the United Kingdom) find that the transition from a fixed regime to a floating regime actually reduces the point estimates of half-life deviations.
By way of contrast, the persistence of RER shocks increases when one moves from a floating regime to a fixed nominal exchange rate regime. For the other RERs under study, this pattern is unclear. However, the change from the interwar to the Bretton Woods regime shows a widespread increase of the RER persistence. And finally, although two important sources of bias have been corrected, in a multivariate framework in which more precise estimates are obtained and the potential heterogeneity across countries in the speed at which shocks dissipate has been taken into account, the degree of RER persistence fluctuations remains an absolute puzzle. Regardless of the monetary regime, the mean-unbiased estimates of half-life deviations are too high to be explained by the stickiness of nominal wages and prices. Only for the interwar period are the point half-life estimates below two years for most countries.
In the empirical analysis of the properties of RERs, it has been implicitly assumed that the underlying data generating process is the same across remote periods of time. In this study, applying powerful econometric tools, it has been proved that taking the structural change in the RER dynamics into consideration generates a substantial bias in the estimation of the RER properties. Furthermore, taking interest in this instability emphasizes another source of bias, namely, working with small samples. This matter has also been treated here.
A great number of permanent shocks have been identified by the univariate analysis. Even though, separately, RERs exhibit specific shocks, a common international pattern seems to emerge. The abandonment of the Classical Gold Standard, after the end of the First World War, and the breakup of the Bretton Woods system seem to have had a significant impact on the behaviour of RERs. Moreover, an additional break in the decade of 1930’s or 1940’s seems to appear. This de facto common pattern has been confirmed by a multivariate analysis in which the interrelation between the different currencies is used in order to obtain more precise estimations of these shocks
The analysis of the persistence of RERs has been carried out taking into account the effect of these shocks. In a multivariate framework, though we still clash with the ‘PPP puzzle’, our results add some ideas to the debate. Firstly, it does not seem rational to rely on the assumption of cross-sectional homogeneity when working with econometric methods for panel data, at least when estimating the confidence intervals of the half-lives. Additionally, this heterogeneity is found not just within a specific monetary regime but also between different regimes. Ignoring this potential heterogeneity only adds a further bias to the persistence estimation. Secondly, although Taylor [1] unwaveringly believes that RER persistence has been stable throughout the twentieth century, this is not apparent. The interwar regime, a period characterized by strong monetary shocks, is the only regime that shows half-life estimates below two years, which is a reasonable period of time for RERs to return to their long-run equilibrium in accordance with the prevailing macroeconomic models. Thirdly, some empirical research has directly linked the nominal exchange regime to the speed at which the RER shocks disappear. Though the sign of this correlation is unclear, Sarno and Valente [17] highlighted that shocks take less time to die out during floating exchange rate regimes. The results described above, nevertheless, show a more ambiguous linkage. We only find a substantial increase in RER persistence in the switch from the interwar to the Bretton Woods regime. Unexpectedly, the latter regime, besides being the most persistent, is extremely heterogeneous.
Accordingly, despite the limitations of our framework (linearity, non-inclusion of deterministic trends), our results open new questions within the RER debate. It is likely that the observed differences in RER dynamics can be attributed to economic policy, that is, that the decisions taken by monetary policymakers cause shocks to be absorbed more quickly.
The main database comes from Taylor [1] updated with the International Monetary Fund’s International Financial Statistics, unless otherwise stated, as follows:
1. End-of-the period annual nominal exchange rates (national currency per U.S. dollar) are collected from 1997 to 2008. For Switzerland, from 1992 to 2008. In eurozone countries, from 1999 onwards, the value of the euro against the U.S. dollar and the irrevocable fixed rates of conversion between national currencies and the euro are used. In the case of Portugal, until 1889, the conversion ₤ 1 = 4500 réis [55] and the value of the British pound against the U.S. dollar [1] are utilized.
2. Price indices are consumer prices. The updated period is indicated (in brackets): Australia, Belgium, Norway, the United Kingdom, the United States (1997-2008); Canada, Japan, Portugal, Spain, Sweden (1948-2008); Denmark, the Netherlands (1949-2008); Finland, France, Italy (1996-2008); Germany (1992-2008) and Switzerland (1993-2008). For Japan, the information of 1880 corresponds to the wholesale price index (Mitchell, 1992) and the period 1881-1947 corresponds to the inflation in Bordo et al. (2001). Switzerland (1880-1992) comes from the Historical Statistics of Switzerland in ‘The Swiss Economic and Social History online database’ (Preise. Table H.1): https://www.eso.uzh.ch/modul4.html.
1 Other studies were focused on a specific monetary regime. For instance: Diebold et al. [56], Culver and Papell [57] and Catão and Solomou [58] analysed the Classical Gold Standard; Eichengreen [38], Taylor and MacMahon [59] and Michael et al. [60] the interwar period and Abauf and Jorion [61], Taylor and Sarno [62] and Gadea et al. [63], among many others, the post-Bretton Woods regime.
2 Murray and Papell [42-44], Cashin and McDermott [45], Caporale et al. [46] and Choi et al. [26], among others.
3 In Hegwood and Papell [4], changes in the autoregressive parameter are not allowed.
4 Throughout the section, to obtain an adequate power of tests for structural change, a trimming parameter of 0.15 is imposed.
5 Taylor [1] rejects the null hypothesis of a unit root in the RER data using a DFGLS test.
6 Bai, Lumsdaine and Stock [64] and Qu and Perron [21] showed that, in systems of multiple equations, more precise estimates are obtained. Qu and Perron [21], moreover, showed that the estimation of a specific break point in an equation may be more precise when the system includes other equations, although these equations do not contain this precise break, as long as the errors are contemporaneously correlated.
7 With the suspicion that the individual disturbances ui,t would not be able to satisfy the classical assumptions of the general linear model, an AR(2) model has also been considered.
8 That is, the resulting regimes must be a minimum length of h.
9 Notice that the simultaneous estimation procedure is computationally intensive since it requires operations of order O T m . Although Qu and Perron [21] discuss a more efficient algorithm, an extension of the algorithm proposed by Bai and Perron [18], we follow a standard grid search.
10 If the MSBIC criterion is utilized for discriminating between these two rival models, a system of AR(1) SUR equations is unequivocally selected.
11 These bias sources have recently been taken into account by Ozer-Balli et al. [65]
12 Data from 1915 to 1918 are removed in an attempt to prevent atypical observations derived from the World War I period which might induced an explosive root into the autoregressive parameters.
13 Some preliminary results are identified by Cheung and Lai [52] and Cashin and McDermott [54]. For a more refined analysis see, for instance, Kanas [66].