Journal of Ergonomics
Open Access
ISSN: 2165-7556
ISSN: 2165-7556
Research Article - (2017) Volume 7, Issue 3
Mechanical stress on articular cartilage and long-duration standing postures are risk factors for hip osteoarthritis progression. This study aims to examine the relationship between hip flexion contracture and the hip-joint contact force in standing postures using computer simulation. A musculoskeletal model composed of seven segments (Head, Arms, and Trunk (HAT) and thighs, shanks, and two feet) was created. Various standing postures (708 variations) were generated, and five hip flexion contracture conditions were set: zero contracture and flexions of 0°, 10°, 20°, and 30°. A standing posture satisfying the hip flexion contracture condition with the minimum sum of the muscle activations was obtained as the optimal standing posture, and the hip-joint contact force in the optimal standing posture was calculated. A sensitivity analysis was conducted by varying four parameters (the objective function, physiological cross-sectional area, force-length relation, and muscle moment arm length). The hip-joint contact force and hip extensor muscle forces (i.e., those of the gluteus maximus, semitendinosus, semimembranosus, and biceps femoris long head) during standing increased with the development of hip flexion contracture. The hip-joint contact force for the standing posture with a 30° hip flexion contracture was almost twice that for the no-contracture condition (8.7 and 3.7 N/kg, respectively). The sensitivity analysis showed that variation of the four parameters did not affect our main finding. The main finding of this study is that hip-joint contact force during standing increases with the development of hip flexion contracture. The findings of this study may help to prevent hip osteoarthritis progression.
Keywords: Standing posture; Hip-joint; Hip flexion; Computer simulation
A patient’s tendency to feel joint pain with increasing Osteoarthritis (OA) severity [1] has been reported and hip-joint pain is a factor that reduces Short Form 36 physical functioning [2] and walking speed [3]. Moreover, Mannoni et al. [4] have reported that hip OA is strongly associated with disability, and Hall et al. [5] have reported that hip OA causes decreased physical functioning on the Western Ontario and McMaster Universities Osteoarthritis Index. Therefore, it is important to prevent hip OA progression via medical treatment. Mechanical stress on articular cartilage is a risk factor for OA progression [6]. In addition, it has been reported that obesity is also a risk factor [7-9], as increased body mass encourages degeneration of the hip-joint articular cartilage. Therefore, it is essential to avoid overloading this articular cartilage.
Although standing postures are necessary in daily life (e.g. in occupational or household work), it has been reported that long-duration standing postures correspond to an increased risk of hip OA [10,11]. Croft et al. [10] have investigated the relationship between hip OA and occupational activity and reported that severe disease is associated with prolonged standing at work. Thus, it is important to clarify standing postures corresponding to low hip-joint loads for hip OA patients employing long-duration standing postures in daily life.
To maintain a standing posture, it is necessary to position the center of mass over a base of support [12,13], and a specific lower-limb-joint range of motion and muscle actions are also required [14]. According to several previous studies, hip OA decreases both the range of motion [15] and muscle strength [5,16]. In particular, we believe that decreased lower-limb-joint range of motion affects standing posture. It has been reported that hip OA (including knee OA) patients have decreased hip extension ranges of motion [15]. We hypothesize that a decreased hip extension range of motion (i.e., hip flexion contracture) affects the hip joint load (i.e., hip-joint contact force) in a standing posture.
Gilleard and Smith [17] have examined the hip-joint moment during a standing task for both obese and normal weight groups. However, no studies have examined the relationship between hip flexion contracture and hip-joint contact force in a standing posture. Knowledge of this relationship may help to prevent hip OA progression in patients who employ long-duration standing postures in daily life. Thus, the purpose of this study is to examine the relationship between hip flexion contracture and hip-joint contact force in a standing posture. As it is ethically difficult to reproduce hip-joint contracture invasively, we examine this relationship using computer simulation.
Musculoskeletal model
A sagittal-plane musculoskeletal model composed of seven segments (Head, Arms, and Trunk (HAT) and thighs, shanks, and two feet) was created and used. The height and weight of the musculoskeletal model were set to 1.7 m and 65.0 kg, respectively. The musculoskeletal model parameters (segment mass and length, center of mass, and ankle joint position relative to foot length) were set according to previous studies [18-21].
Twelve muscles (iliacus, psoas, gluteus maximus, vastus, biceps femoris short head, rectus femoris, semitendinosus, semimembranosus, biceps femoris long head, tibialis anterior, soleus, and gastrocnemius) were actuated in the right lower limb. The musculoskeletal model was assumed to be bilaterally symmetrical, and the twelve muscles in the left lower limb were actuated in the same manner as those in the right lower limb. All muscles were based on the Hill model and were composed of contractile, passive, and series elements (Figure 1). The active force–length curve was obtained via spline interpolation of the force–length curve reported by Zajac [22]. The passive force–length curve was obtained from the function reported by Thelen [23]. The specific muscle tension [24] was set to 61 N/cm2. The muscle moment arm length and muscle fiber length ratio were exported from Lower Limb Model 2010 [24-27] on OpenSim [28]; these values were obtained for each muscle by determining the hip-, knee-, and ankle-joint angles during standing. The pennation angle was not considered in this study.
Standing posture generation
In this study, two constraints were set to generate various standing postures. As it is necessary to position the center of mass on a base of support to maintain a standing posture [12,13], the horizontal component of the center of mass of the musculoskeletal model was set at the midpoint of the foot, as the first constraint. The ranges of motion of the hip, knee, and ankle joints were set from 20° extension to 50° flexion, from 50° flexion to 0° extension, and from 30° plantar flexion to 20° dorsiflexion, respectively, as the second constraint.
First, all ankle- and knee-joint angle combinations were generated (i.e., 51 × 51=2,601 variations). Next, the hip-joint angles satisfying the first and second constraints were calculated. The number of standing postures satisfying the first and second constraints was 708 (Figure 2).
Criteria for determining optimal standing posture
Although there are many choices of hip-, knee-, and ankle-joint angles, an individual unconsciously selects the optimal standing posture from among the various possibilities. A previous study [29] has reported that minimizing muscle activations yields joint motion predictions closest to the average values measured for human subjects. Therefore, a standing posture in which the sum of the muscle activations is at a minimum was assumed to constitute an optimal standing posture.
Calculation of joint moments, muscle forces, and sum of muscle activations
The muscle force and maximum muscle force of a contractile element are needed to calculate the muscle activation. The hip-, knee-, and ankle joint-moments for all standing postures (i.e., the 708 variations) were calculated via inverse dynamics. The active joint moment of each joint was obtained by subtracting the passive joint moment from the net joint moment.
An optimization method to estimate a muscle force has been reported previously [30], wherein differences in the objective function affect the resulting muscle force values. In a simulation study by Yoshioka et al. [21], a sensitivity analysis was conducted using multiple objective functions. In the present study, two objective functions were used to estimate the muscle forces of the contractile elements. The first objective function was the sum of the squares of the muscle activations, and the second objective function was the sum of the squares of the muscle stresses, defined as follows:
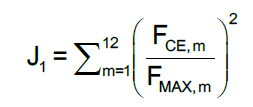 (1)
(1)
Second objective function:
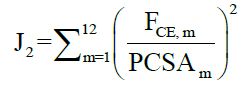 (2)
(2)
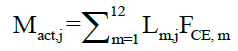 (3)
(3)
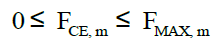 (4)
(4)
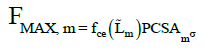 (5)
(5)
The sum of the muscle activations is defined as:
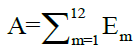 (6)
(6)
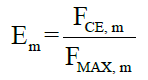 (7)
(7)
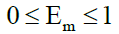 (8)
(8)
The sum of the muscle activations for each standing posture was calculated using the above equations; the variables used are defined as follows:
• m: Muscle number (1-12);
• F CE: Muscle force of contractile element;
• FMAX: Maximum muscle force of contractile element;
• PCSA: Physiological cross-sectional area;
• σ: Specific muscle tension;
• Mact: Active joint moment;
• j: Joint (hip, knee, or ankle);
• L: Muscle moment arm length;
• f ce: Normalized muscle force (active force–length curve);
• L˜: Ratio of muscle fiber length;
• A: Sum of muscle activations;
• E: Muscle activation.
Hip flexion contracture conditions
Five hip flexion contracture conditions were set: zero contracture and flexions of 0°, 10°, 20°, and 30°. As an example, when the hip flexion contracture condition is 20°, the hip-joint angle while standing is greater than 20°.
Calculation of hip-joint contact force
The hip-joint contact force was calculated from the muscle forces across the hip joint (i.e., those of the iliacus, psoas, gluteus maximus, rectus femoris, semitendinosus, semimembranosus, and biceps femoris long head), and the hip-joint force was calculated using inverse dynamics. The coordinate points of the muscle origin and insertion were exported from Lower Limb Model 2010 [24-27] on OpenSim [28]; these values were obtained for each muscle by determining the hip-, knee- and ankle-joint angles during standing. The hip-joint contact force was calculated as follows:
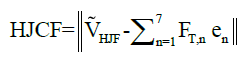 (9)
(9)
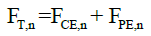 (10)
(10)
Where the variables are:
HJCF: Hip-joint contact force;
V ̃HJF: Hip-joint force vector;
F T: Total muscle force;
n: Number of muscle across hip joint (1-7);
e ̃: Muscle line of action unit vector;
FPE: Muscle force of passive element.
Sensitivity analysis
The hip-joint contact force calculated using the musculoskeletal model was affected by changing the model parameters. Previously, Yoshioka et al. [31] conducted a sensitivity analysis by changing four parameters (the objective function, physiological cross-sectional area, force–length relation, and muscle moment arm length). Therefore, we also conducted a sensitivity analysis by changing four parameters, including the objective function (two options) and the physiological cross-sectional area (three options [24,27,32].
Random values (within ±10%) were added to normalized muscle forces (i.e., f ce (L̃ m) in Equation 5) for each muscle, and modified and normalized muscle forces (i.e., f ' ce, m) were obtained to change the force–length relation. The modified and normalized muscle forces were calculated as follows:
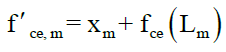 (11)
(11)
Where the variables are:
f ' ce Modified and normalized muscle force;
x: Random value (within the range from -0.1 to 0.1).
When a value of f ' ce was greater than 1, the value was replaced by 1. f ' ce (L ̃m) in Equation 5 was replaced by f ' ce, m for each muscle to change the force-length relation.
The muscle moment arm lengths were set randomly within the range of 90-110% [31]. Figure 3 presents a flowchart of the simulation implemented in this study. The four parameters mentioned above and the hip flexion contracture conditions (five options) were set randomly. The process for obtaining an optimal standing posture was iterated 1,000 times, and we examined the relationships between the hip-joint contact force, joint angle, joint moment, and muscle forces. All script codes for this computer simulation were written in Scilab 6.0.0 (Scilab Enterprises) and in MATLAB R2016a (MathWorks).
Figure 3: Simulation procedure. First, all standing postures were generated and the corresponding joint moments were calculated. Four parameters (the objective function, physiological cross-sectional area, force–length relation, and muscle moment arm length) were set randomly, and the muscle forces during standing were estimated via optimization. Next, the hip flexion contracture condition was set randomly, and the optimal standing postures were obtained. Finally, the hip-joint contact forces in the optimal standing postures were calculated.
Figure 4 shows the relationship between hip flexion contracture and hip-joint contact force in a standing posture. The hip-joint contact force during standing increases with the development of hip flexion contracture. The hip-joint contact forces during standing were obtained as 3.7 ± 0.1, 3.9 ± 0.2, 4.8 ± 0.6, 6.6 ± 0.6, and 8.7 ± 0.4 N/kg for the cases of zero contracture and of hip flexion contractures of 0°, 10°, 20° and 30°, respectively. The hip-joint contact force for the standing posture with a 30° hip flexion contracture was almost twice that obtained for the no-contracture condition.
Figure 5 shows all five standing postures, without and with hip flexion contracture. For the standing posture without hip flexion contracture, the knee joint, hip joint, and top of the HAT are 7.4, 8.6, and 8.9 cm anterior to the ankle joint, respectively. With the development of hip flexion contracture, the hip and knee flexion angles and the ankle dorsiflexion angle increase.
The purpose of this study was to examine the relationship between hip flexion contracture and hip-joint contact force in a standing posture using computer simulation. Our hypothesis was confirmed, and the main finding of this study is that the hip-joint contact force during standing increases with the development of hip flexion contracture (Figure 4). Although several studies [17,33] have examined the hip-joint moment during a standing task, the hip-joint contact force had not been examined. Therefore, the information presented in this study constitutes a new finding.
Table 1 shows the relationship between hip flexion contracture and the joint angle, joint moment, and muscle forces. When the hip flexion contracture increases, the hip and knee flexion angles, the ankle dorsiflexion angle, and the hip and knee extension moments also increase. Moreover, the hip extensor muscle forces (those of the gluteus maximus, semitendinosus, semimembranosus, and biceps femoris long head) also increase.
| Hip flexion contracture conditions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Zero contracture | 0° | 10° | 20° | 30° | ||||||
| Joint angle | ||||||||||
| Hip flexion | -1.5 | (0.4) | 0.6 | (0.3) | 10.3 | (0.2) | 20.2 | (0.1) | 30.3 | (0.0) |
| Knee extension | -8.6 | (0.9) | -11.2 | (2.4) | -22.9 | (4.4) | -30.7 | (3.6) | -37.5 | (2.0) |
| Ankle dorsiflexion | 10.3 | (0.5) | 11.3 | (1.5) | 15.7 | (2.8) | 17.5 | (2.3) | 18.7 | (1.2) |
| Joint moment | ||||||||||
| Hip flexion | -0.01 | (0.00) | -0.02 | (0.02) | -0.09 | (0.04) | -0.20 | (0.03) | -0.32 | (0.02) |
| Knee extension | -0.05 | (0.02) | -0.02 | (0.05) | 0.12 | (0.09) | 0.18 | (0.07) | 0.21 | (0.04) |
| Ankle dorsiflexion | -0.39 | (0.00) | -0.39 | (0.00) | -0.39 | (0.00) | -0.39 | (0.00) | -0.39 | (0.00) |
| Muscle force | ||||||||||
| Iliacus | 0.07 | (0.01) | 0.05 | (0.01) | 0.00 | (0.00) | 0.00 | (0.00) | 0.00 | (0.00) |
| Psoas | 0.13 | (0.05) | 0.12 | (0.05) | 0.06 | (0.02) | 0.03 | (0.01) | 0.00 | (0.00) |
| Gluteus maximus | 0.13 | (0.02) | 0.31 | (0.22) | 1.25 | (0.48) | 2.50 | (0.46) | 3.68 | (0.58) |
| Vastus | 0.26 | (0.20) | 0.98 | (0.94) | 4.11 | (1.70) | 6.06 | (1.59) | 8.10 | (1.14) |
| Biceps femoris: s.h. | 0.15 | (0.03) | 0.13 | (0.02) | 0.07 | (0.01) | 0.04 | (0.01) | 0.02 | (0.01) |
| Rectus femoris | 0.00 | (0.00) | 0.03 | (0.04) | 0.05 | (0.06) | 0.00 | (0.00) | 0.00 | (0.00) |
| Semitendinosus | 0.02 | (0.01) | 0.03 | (0.00) | 0.03 | (0.01) | 0.07 | (0.02) | 0.12 | (0.03) |
| Semimembranosus | 0.03 | (0.02) | 0.06 | (0.05) | 0.14 | (0.15) | 0.52 | (0.19) | 1.15 | (0.35) |
| Biceps femoris: l.h. | 0.02 | (0.01) | 0.03 | (0.02) | 0.08 | (0.06) | 0.29 | (0.10) | 0.59 | (0.20) |
| Tibialis anterior | 0.00 | (0.00) | 0.00 | (0.00) | 0.00 | (0.00) | 0.00 | (0.00) | 0.00 | (0.00) |
| Soleus | 7.36 | (0.42) | 7.45 | (0.44) | 8.08 | (0.57) | 8.31 | (0.65) | 8.49 | (0.63) |
| Gastrocnemius | 2.70 | (0.34) | 2.71 | (0.33) | 2.59 | (0.39) | 2.46 | (0.43) | 2.35 | (0.52) |
Table 1: Relationship between hip flexion contracture and joint angle, joint moment, and muscle forces. Mean (SD) joint angle (°), joint moment (Nm/kg), and muscle force (N/kg) for standing postures without and with hip flexion contracture. s.h.: Short Head; l.h.: Long Head.
Joint moment, muscle forces, and hip-joint contact force during standing
The results of this study show that the hip and knee flexion angles, ankle dorsiflexion angle, and hip and knee extension moments increase when hip flexion contracture develops (Table 1). This result agrees with the findings of a previous simulation study [34]. When the hip joint is flexed via hip flexion contracture during standing, the center of mass moves forward, and the hip extension moment increases. Therefore, the knee extension moment may also increase in order to suppress an excessive increase in the hip extension moment. However, the ankle joint moment does not change with increased hip flexion contracture. In this study, the center of pressure was assumed to be located at the midpoint of the foot segment. Moreover, the horizontal component of the ground reaction force was assumed to be zero in this study because of the static standing posture. For these reasons, the ankle joint moment did not change with increased hip flexion contracture.
Furthermore, the hip extension muscle forces (i.e., those of the gluteus maximus, semitendinosus, semimembranosus, and biceps femoris long head) were found to increase with increased hip flexion contracture (Table 1). Note that the joint moment is the sum of the product of the muscle moment arm length and the muscle force for each muscle across a joint (Equation 3). Thus, the hip extension muscle forces increase with increased hip extension moment.
Moreover, the hip-joint contact force is affected by the muscle forces across the hip joint (Equation 9) and the hip-joint moment (Equation 3). We believe that increased hip extensor muscle forces are the cause of the increased hip-joint contact force. Although the joint moment is often used instead of a joint load index, the former property is not exactly a joint load index. A previous study [35] has reported that a decreased knee-joint moment does not guarantee a knee contact force.
Therefore, in this study, it was considered appropriate to use the joint contact force as a joint load index.
The hip-joint contact force for the standing posture with zero contracture found in this study (3.7 N/kg) was smaller than that reported by Bergmann et al. [36] (approximately 7.5 N/kg) and that by Davy et al. (1 body weight, i.e., 9.8 N/kg) [37]. The likely cause for this difference is that a sagittal musculoskeletal model was used in this study, with the muscle forces in the frontal plane being neglected. A previous study [38] examined hip joint moments during a squat; it found that when the hip flexion angle was 0° (i.e., a standing posture), a hip abduction moment was within the range of approximately −10 to 20 Nm. In this study, for example, if the hip abduction moment during the standing posture is assumed to be 10 Nm, the hip-joint contact force at the frontal component is roughly 3.7 N/kg, as calculated from (10 Nm/0.042 m)/65 kg. (The value 0.042 m is the muscle moment arm length of the gluteus medius from Lower Limb Model 2010 [24-27] on OpenSim [28]). In other words, the hip-joint contact force of 7.4 N/kg (calculated from 3.7 N/kg (sagittal component in this study)+3.7 N/kg (tentative frontal component)) is close to the values found in the previous studies [36,37], and the hip-joint contact force added to that of the tentative frontal component is quantitatively reasonable.
Moreover, the standing postures in Figure 5 are similar to the initial phases of a squat. A previous study [38] also reported that when the hip flexion angle during a squat increased from 0° to 30°, the hip abduction moment in the phase did not change very much within approximately -10-20 Nm. Therefore, it is unlikely that development of a hip flexion contracture causes a change in the hip abduction moment and hip-joint contact force in the frontal component during a standing posture.
In this study, it was possible to obtain the main finding that the hip-joint contact force during standing increases with hip flexion contracture. However, a new method may be required to obtain a realistic value for the hip-joint contact force during standing, and a three-dimensional musculoskeletal model should be used in the future to determine a realistic hip-joint contact force during standing.
Validity of criteria for determining optimal standing posture and sensitivity analysis
Regarding the standing posture without hip flexion contracture (Figure 5), the knee joint, hip joint, and top of the HAT were anterior to the ankle joint by 7.4, 8.6, and 8.9 cm, respectively. Woodhull et al. [38] have examined the positions of standing posture landmarks in healthy people. In their study, the knee joint, hip joint, and ear were found to be anterior to the ankle joint by 3.8, 6.2, and 5.9 cm, respectively. The relative positions of the landmarks in the standing posture with zero contracture considered in this study were almost identical to those of Woodhull et al. [38] and the landmark alignment for the standing posture with zero contracture was almost perpendicular to the floor. These results suggest that the criterion for determining optimal standing postures employed in this study (i.e., minimization of the sum of the muscle activations) is reasonable.
Moreover, we conducted a sensitivity analysis, as the hip-joint contact force is affected by the parameters of the musculoskeletal model. Although the simulation was executed 1,000 times and the parameters (the objective function, physiological cross-sectional area, force–length relation, and muscle moment arm length) were randomly adjusted, the main finding of this study was not greatly affected. Hence, the main finding that the hip-joint contact force during standing increases with hip flexion contracture is reasonable.
Mechanical stress on articular cartilage is a risk factor for OA progression [6], and it has been reported that long-duration standing increases the risk of hip OA [10,11]. As noted above, the results of this study suggest that the hip-joint contact force during standing increases with hip flexion contracture. Therefore, a decreased hip extension range of motion may encourage progression of hip OA in patients who employ long-duration standing postures in their daily lives.
Firstly, although in reality the trunk moves with flexion or extension in the sagittal plane, in this study the trunk was assumed to be a single segment. Therefore, if hip flexion contracture occurs in reality, a different compensatory standing posture may appear (e.g., trunk extension). Secondly, the hip-joint contact force during standing with a hip flexion contracture of 30° was found to be almost twice that for the zero-contracture case in this study. However, this value is smaller than previously reported values for walking, ascending (or descending) stairs, and sitting-to-standing (or standing-to-sitting) motions [36,37,39-41]. It is unclear whether the difference between the hip-joint contact force during standing with zero contracture and that with hip flexion contracture is meaningful. Hence, a cohort study examining the relationship among hip flexion contracture, standing posture duration and OA stage is required.
We examined the relationship between hip flexion contracture and hip-joint contact force in a standing posture using computer simulation.
We concluded the following from the results of this study:
1. The hip-joint contact force in the standing posture increases with hip flexion contracture.
2. The reason for the above effect is that the hip extensor muscle forces (i.e., those of the gluteus maximus, semitendinosus, semimembranosus, and biceps femoris long head) increase.