Journal of Physical Chemistry & Biophysics
Open Access

Relativistic Clocks and the Nature of Time

Richard Oldani^{* *}Correspondence: Richard Oldani, Illinois Institute of Technology, Clymer, New York, USA, Email:

Author info »

Introduction

The concept of time

Of the four dimensions verifiable through experience, time is the least understood. Before clocks were invented, St. Augustine described the problem in a way that still applies today, “What then is time? If no one asks me, I know what it is. If I wish to explain it to him who asks, I do not know.” We have the ability to measure time with incredible accuracy using atomic clocks; and though we all agree about clock properties and how time is measured there is no consensus on how to interpret what is being measured [1-4]. The stumbling block preventing an improved understanding, we shall maintain here, is quantum mechanics. The foundations of quantum mechanics are formulated with respect to inertial systems, so they are only valid for experiments performed in the absence of gravitational fields. However, recent clock experiments are able to distinguish gravitational potential differences of less than a millimetre with no theoretically predicted minimum separation [5]. This means that for all intents and purposes gravitational potentials are continuously differentiable. The extreme accuracy of atomic clocks, which was unknown to the founders of quantum mechanics, suggests that all theories of mechanics, also quantum mechanics, should take into account gravitational fields by being formulated in non-inertial frames.

Quantum mechanical time

In nonrelativistic quantum mechanics clocks are devices that read out a one-dimensional sequence of increasing numbers so that clocks and time are treated operationally as one and the same thing. Time is not an observable in quantum mechanics. Observables are measured by bringing a measuring device into contact with the physical system and different values of the observable are obtained depending on the state of the system. In quantum mechanics time measurements are performed without making contact with the observed physical system, a clock. So the time “measured” by clocks is not a quantum mechanical observable. It is just a numerical parameter, one of four coordinates, the same as in classical physics, and clocks are treated as simple measuring devices of absolute time.

Relativistic time

Atomic clocks are quantum oscillators consisting of electrons that transition between orbitals while registering time as a series of ticks. However, the time clocks measure is relativistic in nature and varies continuously according to a clock’s motion and gravitational potential. In order to calculate the passage of time on the earth’s surface corrections are routinely applied to satellite time based on factors such as velocity and altitude relative to the earth’s surface that are unrelated to clock function. Clock corrections are applied, but without knowing from a quantum mechanical perspective why it is necessary. In other words, clocks register ticks absolutely in rigid succession, but time is perceived relativistically as a continuous variable. If clocks are conceived of as operationally singular mechanisms that indicate time with a string of ticks caused by a transitioning electron, then it is difficult to comprehend how the electron, transitioning within the atom in a regular way, is able to process inputs from two physically distinct external sources, velocity and gravitational potential. Moreover, corrections made to orbiting clocks due to velocity and gravitational potential are applied simultaneously and currently there is no way to describe the effect of two independent physical variables at a single point.

Literature Review

Properties of quantum systems

There is ample experimental evidence to show that the rate of an atomic clock is simultaneously influenced by its position and its motion with respect to a gravitational field. The ticks of a clock are equivalent to electron cycles, but it is not immediately clear how an electron is able to alter its rate of oscillation as it changes energy states in an atomic clock. We can hold gravitational potential constant to determine how clock rate varies with respect to velocity or we can hold velocity constant to determine the dependency of clock rate on gravitational potential, but we cannot derive an equation to describe clock rate with respect to both variables simultaneously. Therefore it is impossible to derive an equation of motion for clocks in a gravitational field that can predict experimental results. This is why theories have been proposed that assign general relativistic effects to space-time geometry acting at the Planck level, as suggested by loop quantum gravity. A theory of that type would be beyond the possibility of experimental verification.

A possibility that has not been tried is to follow Einstein’s classically inspired approach based on the equivalence principle and ask if it is possible for an electron to change its rate of oscillation as it transitions between discrete energy states in an atomic clock. In fact there is considerable experimental evidence that quantum systems evolve continuously during changes of state. The quantum Zeno effect [6], for example, “describes the situation in which the time evolution of any quantum system can be slowed by sufficiently frequent ‘observations’”, where “slowing” refers to induced changes in an electron’s classically defined equations of motion and intervention occurs by means of “a direct interaction, for example with an external field”. The external fields referred to in these experiments are electromagnetic, but it is hypothesized that gravitational fields could have the same effect through intermediation of the equivalence principle.

Additional evidence that classical equations may be used to describe the continuous motion of an electron transitioning between energy levels is obtained from “Penning traps”. Single electrons are trapped by surrounding them with a homogeneous axial magnetic field and an inhomogeneous quadrupole electric field while non-demolition measurements are performed [7]. The trapped electron constitutes an artificial atom or “quantum cyclotron”, the simplest quantum mechanical system possible. Applying a magnetic field to the trap causes the electron to execute two different types of motion simultaneously; circular orbits perpendicular to the field and axial drifts parallel to it. Continuously applied corrections to the electron’s equations of motion are found to be necessary due to “relativistic shifts” of mass and energy levels. It is hypothesized that the relativistic effects induced in a Penning trap are physically equivalent to relativistic effects imposed by the equivalence principle and reflect a symmetry between electromagnetic and gravitational fields at the microscopic level.

Due to their extreme sensitivity atomic clocks can detect the gravitational potential difference of a crystal lattice’s upper and lower surfaces, a distance of one millimetre [5]. The authors conclude, “These results suggest that there are no fundamental limitations to inter-clock comparisons reaching frequency uncertainties at the 10^-21 level, offering new opportunities for tests of fundamental physics.” The fact that there are “no fundamental limitations to inter-clock comparisons” means that interactions between gravitational fields and quantum oscillators are only limited by our ability to differentiate between clocks spatially; that is, by the granularity of matter itself. The continuity of gravitational potential suggested by atomic clock experiments indicates that gravitational exchanges of energy occur continuously.

Non-inertial coordinate systems

We have experimental proof that electron motion is affected by outside influences as it transitions continuously between energy states [5-7]. The extremely short distance the electron travels, the tiny duration of its path, and the infinitesimal changes produced by gravitational potentials mean that the curvature of space-time may be neglected. Therefore within the infinitesimally small space-time region of the atom the equivalence principle is not just an approximation it is exactly true and the motion of the electron is subject to the laws of special relativity. Because gravitational fields are free to interact with atomic electrons time can no longer be thought of as “a one-dimensional sequence of increasing numbers”. Due to the equivalence principle additional dimensions are introduced by velocity and gravitational acceleration causing variation in the ticks of a clock.

We require equations of motion for an oscillating electron that is subject to simultaneous corrections of velocity and acceleration. The same property of light that allows astronomers to measure the distance of objects at the edge of the universe (spatial linearity) and compare periods of oscillation due to red shifts (temporal linearity) can be used to probe atomic structure. Consider a well-known test for relativity theory using Caesium beam atomic clocks based on the 133Cs isotope. The clocks are flown around the world first in an eastward and then in a westward direction, and later compared to a laboratory clock fixed on the earth’s surface [8]. The experiment demonstrates a slowing of clocks Δt_k that is greatest in the eastward direction of flight due to the earth’s rotation and a speeding up of clocks Δt_g at higher altitudes due to an increased gravitational potential. They are relativistic corrections to the time of the system clock TS in the airplane which cannot be interpreted by a nonrelativistic model of clocks because they are located in a noninertial system of coordinates. When Δt_k and Δt_g are summed at the end of the flight they will equal the time on the atomic clock TL in the laboratory.

T_L = T_S − Δt_g + Δt_k …. (1)

Because the clock rate is locally determined both on the airplane and at the laboratory the frequency of the Cs atoms, 9,192,631,770 Hz, does not change during the approximately one week duration, ΔT ≈ 6×10⁵ sec, of the flights.

However, during that time period T_S speeds up relative to T_L an amount equal to approximately 2.7 x 10^-7 seconds due to the combined influence of clock velocity and gravitational potential. The corrections are due to the relative velocity and altitude of the airplane, so they occur simultaneously.

The linearity of time allows the classical interval ΔT , or time of flight of the airplane, to be subdivided into a series of identically constituted clock cycles of period τ that sum linearly.

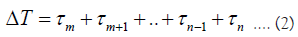
Where τ_m is the first clock cycle and τ_n is the last clock cycle. The clock periods τ correspond to single ticks of the clock, complete cycles of a transitioning electron between excited and ground states. Each of the cycles includes an infinitesimal correction with respect to the laboratory clock and their sum gives the total correction factor in equation 1. The correction for each clock cycle is calculated by dividing the total correction by the approximate number of oscillations during the measurement period ΔT . The linear correction factor that must be applied to the clock period τ due to gravitational field is,

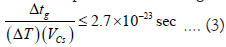
This corresponds to an uncertainty in the electron’s path length for each period of oscillation of ct = Δλ ≤ 8.1×10⁻¹⁵m . It is a distance that is much smaller than the indeterminacy of an electron relative to the nucleus due to the wavelength,

λ = 3.26×10−2m

An even lower uncertainty in the electron’s path length is obtained from the latest atomic clock experiment with fractional frequency instability, Δf / f , equal to 7.6 × 10^-21 [6].

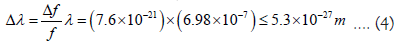
The measurement of time and wavelength in an atomic clock is not governed by the uncertainty principle because clock ticks are quantum non-demolition measurements; that is, the uncertainty of the ticks does not increase from its measured value as the system evolves. It is a determination of the maximum thickness of the electron shell and indicates the level of spatial precision necessary for periodic electron transitions. In other words, if the surfaces of the atom and its excited states were not completely uniform electron transitions would not be of constant duration and clock ticks would be irregular.

Differential equations of motion

Due to experimentally confirmed corrections applied to atomic clocks in satellites and elsewhere we conclude that the electron of an atomic clock oscillates with relativistic correction to each cycle Δt (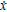) due to angular velocity relative to the centre of the earth and correction to each cycle due to an acceleration of coordinates Δt (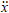) between ticks of the clock. An electron in free space accelerates under the influence of a gravitational field due to its mass by undergoing a change in velocity; however, an atomic electron cannot accelerate in the same way as a free electron because the spacing between electron shells is an invariant. To describe the influence of gravitational fields on the electron of an atom we use Minkowski space, hold the spatial coordinates constant, and let time vary. The use of Minkowski space has the advantage that the space-time distance of an electron transition is invariant, so that all local frames of reference will agree on the total distance in space-time between the ticks of a clock. The invariant properties of Minkowski space make it indispensable to a description of atomic structure. It allows a classical equation of motion for the transitioning electron to be derived as a variation of time with respect to space.

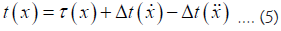
Where τ (x) is the invariant clock period of the atom, Δt (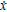) represents a correction due to kinematical time dilation, and Δt (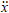) represents a speeding up of time due to increases in gravitational potential. By letting Δt go to 0 for the region of space-time between electron orbitals we obtain a differential equation of motion. That is, clock rate variation is described continuously with respect to electron motion in a gravitational field. No other equation can describe the simultaneous influence of velocity and acceleration that is routinely applied to satellite clocks.

Integral equations of the motion

Using Hamilton’s principle function S=∫Ldt and making use of the differential equation of motion (5), we wish to describe clock motion in a gravitational field as a variational problem. The Lagrangian describes the time evolution of an atomic clock (electron excitation and decay) in generalized coordinates between two specified points in time and bounded in space by the electron shells, where the path the electron follows between the initial and final stationary points is the one which minimizes the action. The integral equation describing the electron’s path in angular measure takes a function as its input L(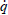(t ), q(t ),t )dt and returns a scalar (reduced Planck’s constant), where q (position) is expressed in generalized coordinates coincident with the electron shells.

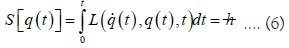
In other words, the action minimum of a clock and Hamilton’s principle are synonymous. The action S[q(t )] is a relativistic equation which treats time symmetrically with the space coordinates. The generalized coordinates describe the electron’s path in a configuration space consisting of three coordinates that define the origin, or nucleus, and three coordinates that define the manifold on which the electron is constrained to move (the electron shells). Solving for the action we obtain an equation describing the cycles of a quantum oscillator, which are the individual ticks of an ideal clock.

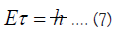
The integration limits in (6) designate a discrete time interval making a clear departure from the continuous time evolution of the wave function. It is hypothesized that the action functional (6) and the differential equation (5) are the only equations of motion that successfully describe simultaneous changes in velocity and gravitational potential that occur in GPS satellites.

Discussion

A long ignored problem of quantum mechanics is the absolute nature of space-time; or more precisely, space and time [9]. Quantum mechanical and relativistic concepts of space-time are reconciled here by formulating a fully relativistic description of an atomic clock given by equation (6). By relativistic we mean that electron oscillation occurs as a continuous evolution in real time, as opposed to the nonrelativistic Hamiltonian descriptions of 1.2 which choose a particular, or absolute time.

Conclusion

The interaction of an atomic clock with a gravitational field is analysed to determine how relativistic properties of time are manifested at the microscopic level. Hamilton’s principle is used to obtain an integral equation of motion. Time’s dual nature is evident in the emission and absorption of radiation, lifetimes of particles, and radioactivity. Theories suggesting that time is only continuous, or an emergent property of matter, fail to include the properties of time measurement as determined by clocks, which are the only objectively verifiable descriptions of time available. Evaluations of time that cannot account for satellite clock behaviour are incomplete because they are not symmetric in the coordinates, are incompatible with relativity theory, and are unsubstantiated by experiment.

References

1. Smolin L. Time reborn: From the crisis in physics to the future of the universe. HMH. 2013.

   [Google Scholar]

2. Hawking S. A brief history of time. Bantam Books. 1998.
3. Rovelli C. The order of time. Riverhead Books. 2018.
4. Carroll SM. The biggest ideas in the universe: Space, time and motion. Random House. 2022.
5. Bothwell T, Kennedy CJ, Aeppli A, Kedar D, Robinson JM, Oelker E, et al. Resolving the gravitational redshift within a millimeter atomic sample. Nature. 2022;602:420-424.

   [Crossref] [Google Scholar]

6. Itano WM. Perspectives on the quantum Zeno paradox. J Phys. 2009;196(1)012018.

   [Crossref] [Google Scholar]

7. Brown LS, Gabrielse G. Geonium theory: Physics of a single electron or ion in a Penning trap. Rev Mod Phys. 1986;58(1):233.

   [Crossref] [Google Scholar]

8. Hafele JC, Keating RE. Around-the-world atomic clocks: Observed relativistic time gains. Science. 1972;177(4044):168-170.

   [Crossref] [Google Scholar]

9. Weinstein S. Absolute quantum mechanics. Br J Philos Sci. 2001;52(1):67-73.

   [Crossref] [Google Scholar]