In clinical research and development, it is always a concern to the principal investigator that (i) the research finding does not reach statistical significance, i.e., it is purely by chance alone, and (ii) the significant research finding is not reproducible under the same experimental conditions with the same experimental units. Typical examples include (i) results from genomic studies for screening of relevant genes as predictors of clinical outcomes for building of a medical predictive model for critical and/or life-threatening diseases are often not reproducible and (ii) clinical results from two pivotal trials for demonstration of safety and efficacy of a test treatment under investigation are not consistent.

In practice, it is then of particular interest to assess the validity/ reliability and reproducibility of the research findings obtained from studies conducted in pharmaceutical and/or clinical research and development.

For genomic studies, thousands of genes are usually screened for selecting a handful of genes that are most relevant to clinical outcomes of a test treatment for treating some critical or life threatening diseases such as cancer. These identified genes which are considered risk factors or predictors will then be used for building a medical predictive model for the critical or life threatening diseases. A validated medical predictive model can definitely benefit patients with the diseases under study. In practice, it is not uncommon that different statistical methods may lead to different conclusions based on the same data set, i.e., different methods may select different group of genes that are predictive of clinical outcomes. The investigator often struggles with the situation that (i) which set of genes should be reported, and (ii) why the results are not reproducible. Some researchers attribute this to (i) the method is not validated and (ii) there is considerable variability (fluctuation) in data. Thus, it is suggested that necessary actions be taken to identify possible causes of variabilities and eliminate/control the identified variabilities whenever possible. In addition, it is suggested the method should be validated before it is applied to the clean and quality database.

For approval of a test drug product, the United States (US) Food and Drug Administration (FDA) requires two pivotal studies be conducted (with the same patient population under the same study protocol) in order to provide substantial evidence of safety and efficacy of the test drug product under investigation. The purpose for two pivotal trials is to assure that the positive results (e.g. p-value is less than the nominal level of 5%) are reproducible with the same patient population under study. Statistically, there is higher probability of observing positive results of future study provided that positive results were observed in two independent trials as compare to that of observing positive results provided that positive results were observed in one single trial. In practice, however, it is a concern whether two positive pivotal trials can guarantee whether the positive results of future studies are reproducible if the study shall be repeatedly conducted with the same patient population.

In clinical research, to increase the creditability of the research findings in terms of accuracy and reliability, it is often suggested that testing and/or statistical procedure be validated for reducing possible deviation/fluctuation in research findings. This, however, does not address the question that whether the current observed research findings are reproducible if the study shall be conducted repeatedly under same or similar experimental conditions with the same patient population. In this short commentary, we recommend the use of a Bayesian approach for assessment of the reproducibility of clinical research.

In other words, the variability (or degree of fluctuation) in research findings is first evaluated followed by the assessment of reproducibility probability based on the observed variability [1]. The suggested method provides certain assurance regarding the degree of reproducibility of the observed research findings if the study shall be conducted under the same experimental conditions and target patient population.

In practice, reliability, repeatability, and reproducibility of research findings are related to various sources of variability such as intrasubject (experimental unit) variability, inter-subject variability, and variability due to subject-by-treatment interaction and so on) during the pharmaceutical and/or clinical development process. To achieve the desired reliability, repeatability, and reproducibility of research findings, we will need to identify, eliminate, and control possible sources of variability. Chow and Liu [2] classified possible sources of variability into four categories: (i) expected and controllable (e.g. a new equipment or technician), (ii) expected but uncontrollable (e.g. a new dose or treatment duration), (iii) unexpected but controllable (e.g. compliance), and (iv) unexpected and uncontrollable (e.g. pure random error). In pharmaceutical/clinical research and development, these sources of variability are often monitored through some variability (control) charts for statistical quality assurance and control (QA/QC) [3,4]. The selection of acceptance limits, however, is critical to the success of these control charts. Following the idea of Shao and Chow [1], Salah et al. [5] proposed the concept of reproducibility based on an empirical power for evaluation of the degree of reliability, repeatability, and reproducibility which may be useful for determining the acceptance limits for monitoring reliability, repeatability, and reproducibility in variability control charts.

For marketing approval of a new drug product, the FDA requires that at least two adequate and well-controlled clinical trials be conducted to provide substantial evidence regarding the safety and effectiveness of the drug product under investigation. The purpose of conducting the second trial is to study whether the observed clinical result from the first trial is reproducible on the same target patient population. Let H0 be the null hypothesis that the mean response of the drug product is the same as the mean response of a control (for example, placebo) and Ha be the alternative hypothesis. An observed result from a clinical trial is said to be significant if it leads to the rejection of H0. It is often of interest to determine whether clinical trials that produced significant clinical results provide substantial evidence to assure that the results will be reproducible in a future clinical trial with the same study protocol. Under certain circumstances, the FDA Modernization Act (FDAMA) of 1997 includes a provision (Section 115 of FDAMA) to allow data from one adequate and well-controlled clinical trial investigation and confirmatory evidence to establish effectiveness for risk/benefit assessment of drug and biological candidates for approval. Suppose that the null hypothesis H0 is rejected if and only if |T|>C, where T is a test statistic and c is a positive critical value. In statistical theory, the probability of observing a significant clinical result when H_a is indeed true is referred to as the power of the test procedure. If the statistical model under H_a is a parametric model, then the power is

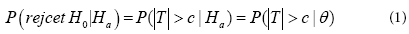
Where θ is an unknown parameter or a vector of parameters under H_a. Suppose that one clinical trial has been conducted and the result is significant. What is the probability that the second trial will produce a significant result, that is, the significant result from the first trial is reproducible? Mathematically, if the two trials are independent, the probability of observing a significant result from the second trial when Ha is true is still given by Equation (1), regardless of whether the result from the first trial is significant or not. However, information from the first clinical trial should be useful in the evaluation of the probability of observing a significant result in the second trial. This leads to the concept of reproducibility probability, which is different from the power defined by Equation (1).

Goodman [6] considered the reproducibility probability as the probability in Equation (1) with θ replaced by its estimate based on the data from the previous trial. In other words, the reproducibility probability can be defined as an estimated power of the future trial using the data from the previous trial.

Shao and Chow [1] studied how to evaluate the reproducibility probability using Equation (1) under several study designs. When the reproducibility probability is used to provide an evidence of the effectiveness of a drug product, the estimated power approach may produce a rather optimistic result. A more conservative approach is to define the reproducibility probability as a lower confidence bound of the power of the second trial. Alternatively, a more sensible definition of reproducibility probability can be obtained by using the Bayesian approach. Under the Bayesian approach, the unknown parameter θ is a random vector with a prior distribution π(θ) assumed to be known. Thus, the reproducibility probability can be defined as the conditional probability of |T|>C in the future trial, given the data set x observed from the previous trial, that is,

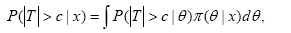
Where, T=T(y) is based on the data set y from the future trial and π(θ|x) is the posterior density of θ, given x. In practice, the reproducibility probability is useful when the clinical trials are conducted sequentially. It provides important information for regulatory agencies in deciding whether it is necessary to require the second clinical trial when the result from the first clinical trial is strongly significant.

Note that power calculation for required sample size for achieving a desired reproducibility probability at a pre-specified level of significance can be performed with appropriate selection of prior.

In practice, if a significant research finding is not reproducible, there is a reasonable doubt that the observed finding could be purely by chance alone and hence is not reliable. Statistically, a research finding is considered not creditable if does not reach statistical significance (i.e., the observed finding is purely due to chance) and it is not reproducible under similar experimental conditions. To increase the creditability of the observed research findings, it is suggested that possible sources of bias and/or variability including (i) expected/controllable, (ii) expected but uncontrollable, (iii) unexpected but controllable, and (iv) unexpected/uncontrollable be identified, eliminated/minimized, and/ or controlled whenever possible in order to increase reliability and the probability of reproducibility for an unbiased and reliable assessment of the test treatment under investigation in the pharmaceutical/clinical research and development process.

In summary, a non-reproducible research finding is not considered a valid science and hence may be biased and hence misleading in pharmaceutical/clinical research. It is then strongly suggested that given the observed research findings, the probability of reproducibility be assessed using the recommended method described in this short editorial article.