Journal of Research and Development
Open Access

Research on Calibration of Moisture Diffusion Coefficient for Wood Drying Based on Drying Simulation

Jibing Qiaoa^* and Zhaoxin Meng ^*Correspondence: Jibing Qiaoa, College of Mechanical and Electrical Engineering, Northeast Forestry University, Hei- longjiang, People's Republic of China, Email:

Author info »

Introduction

Wood drying is a crucial step in the production and manufacturing process of wooden products. Through drying, wood can effectively prevent damage such as decay, insect infestation, deformation and cracking. The drying process of wood is a complex nonlinear heat and mass transfer process. In practical drying operations, it is often controlled by personnel based on experience, making it difficult to quantify and control the parameters accurately. This leads to resource wastage and increased energy consumption [1]. Using Computational Fluid Dynamics (CFD) to simulate the wood drying process allows for obtaining characteristic parameters of wood drying and predicting real drying conditions. This provides a basis for optimizing the design of production applications and drying equipment.

The moisture diffusion coefficient is an extremely important parameter in diffusion models, and it is crucial for the analysis and research of these models [2,3]. When wood is below the fiber saturation point, moisture primarily undergoes non-steady-state diffusion. By employing Fick's second law as the model, the diffusion coefficient of moisture in birch wood was measured using the non-steady-state method at different temperature conditions. This aims to provide theoretical parameters for the numerical simulation of wood drying processes and support the effective simulation of actual drying processes with data.

The reduction of moisture content during the wood drying process has a significant impact on the quality and performance of the wood. The calibration of moisture diffusion coefficient is essential as it determines the rate of moisture migration within the wood, thereby optimizing process control and efficiency in wood drying. By calibrating the moisture diffusion coefficient, one can obtain the diffusion rate of moisture in wood under different conditions such as temperature, humidity and pressure. This information can help establish optimal parameters and strategies for the drying process, improving efficiency, stability and usability of the wood drying process.

In previous wood drying simulations, the pathways and coefficients of moisture diffusion were often based on empirical and default values. However, in this study, the drying reference of birch wood was used as a basis. By measuring the moisture content changes in the specimens and applying the diffusion coefficient formula, the moisture diffusion coefficient of birch wood was determined. Finally, the calibrated diffusion coefficient was integrated with the drying simulation to enhance the accuracy of wood drying simulation results. This approach provides a reliable method for calibrating moisture diffusion coefficients and improves the accuracy of wood drying simulation.

Materials and Methods

Materials

The wood used in this study was sourced from Harbin, China. The selected birch wood samples were free from significant defects and showed no signs of insect infestation. The samples were processed to dimensions of 200 mm in length, 100 mm in width, and 30 mm in thickness, with a smooth surface finish.

Birch wood drying reference

This study adopts the material property method to specify the drying reference for birch wood. This method is characterized by its wide sample coverage, high scientific rigor, and shorter time required establishing the drying reference [4], as shown in (Table 1).

Table 1: Experimental wood drying standard.

Table 2: Moisture diffusion co-efficient at each stage of wood moisture content.

Due to experimental equipment errors, high moisture content gradients were selected as the measurement reference to ensure the rationality of the experimental results and the accuracy of the simulation results.

Experimental method

Non-steady-state method for measuring moisture diffusion coefficient: The experimental equipment used was a DHG-9023A bench top drying oven, the dimensions of the drying chamber are 420 × 350 × 350 (mm). The MP6000 electronic balance with an accuracy of 0.01 g was used.

Considering that the dimensions of the specimens in the length and width directions are much larger than in the thickness direction, moisture primarily moves radially along the wood during the drying process. In this study, only the moisture movement in the thickness direction of the specimens was investigated. The other four directions of the specimens were sealed with epoxy resin and wrapped in aluminum foil to ensure that moisture loss only occurs in the thickness direction.

The process involves weighing the pre-determined moisture content wood samples and placing them in a thermostatic drying oven for drying. The weight of the specimens is measured every 0.5 hours using an electronic balance, and the moisture content is calculated using the moisture content formula. When the equilibrium moisture content is reached, the specimens are transferred to a drying oven until they reach bone dry condition. The corresponding dimension- less transfer potential is calculated based on the mass conversion, and then the diffusion co-efficient is determined through conversion.

Theory: Every 0.5 hours, the moisture content of the wood specimens was measured according to the GB/T1931-2009 Method for determination of moisture content of wood.

The moisture content formula: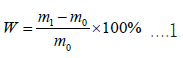

In Equation (1): W is the wood moisture content (%), m1 is the mass of the specimen during the test (g) and m0 is the mass of the specimen in the bone-dry condition (g).

Dimensionless transfer equation: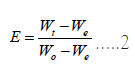

In Equation (2): Wt is the moisture content of wood at a certain moment (%), We is the equilibrium moisture content of wood (%) and W0 is the Initial moisture content of wood (%).

Under isothermal conditions, the non-steady-state diffusion of moisture in wood is governed by Fick's second law, and the mathematical equation for one-dimensional moisture movement is represented by the following partial differential equation:

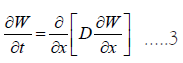
In Equation (3): t is the dimensionless time (s), x is the distance to the center layer of the wood board along the direction of moisture diffusion (cm) and D is the moisture diffusion co- efficient (cm²/s). During the drying process, the diffusion coefficient varies with changes in drying conditions and is considered an unstable value. Therefore, the diffusion coefficient calculated at E=0.5 represents the average value for the entire drying process.

This study makes the following assumptions for the Fick's diffusion equation: (1) The assumption is that the moisture content is uniformly distributed within the wood material. (2) The assumption is that the drying environment remains constant throughout the process. (3) The assumption is that the dimensions of the wood do not change during the drying process. (4) The assumption is that the instantaneous moisture on the wood surface reaches equilibrium with the drying environment during the moisture diffusion process. When the E=0.5, substituting the values of W=We and x= ±L into the Fick's diffusion equation, we can obtain:

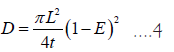
Establishment of heat and mass transfer models: Assuming that mass transfer in wood only occurs during the diffusion process, the coupled heat and mass transfer equations are solved to establish a threedimensional porous media model. The heat transfer equation and mass transfer equation during the simulation heat treatment process of wood are represented by equations (5) and (6) respectively:

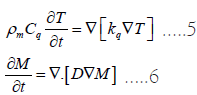
In Equation (5) and (6): ρm iAs the wood density (kg/m³), Cq is the specific heat capacity, Δ is the Nabla operator, T is the temperature (K), κ_q is the thermal conductivity (W/(m.K)), M is the moisture content (%) and D is the diffusion coefficient (cm²/s).

Geometric modeling and mesh generation

In this study, the experimental dimensions of birch wood are used for modeling and simulation. The wood has a length of 200 mm, width of 35 mm, and height of 30 mm, as shown in (Figure 1). The moisture content detection during the simulation is based on the volumetric average moisture content of the wood.

Figure 1: Space claim modeling of the shape.

The geometry is meshed using fluent meshing software. To ensure the accuracy of the simulation results, an unstructured mesh is employed in this model, with a higher mesh density on the wood surface.

Results

Experimental results

Based on the drying benchmark, birch wood samples with different initial moisture content were selected and placed under different temperature conditions. The moisture content of the wood was regularly measured and the corresponding dimensionless transfer potential was calculated, as shown in (Figure 2).

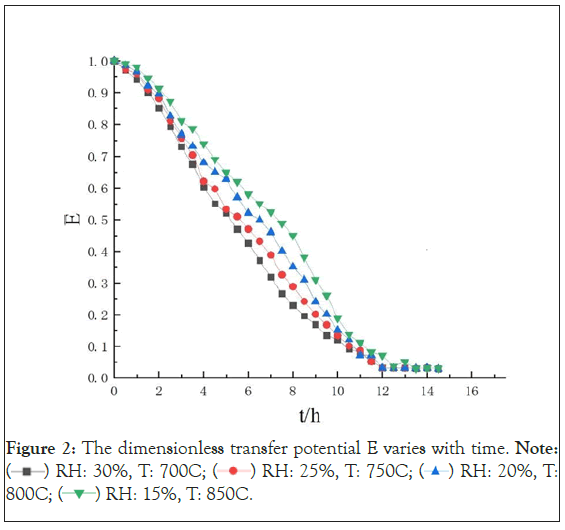
Figure 2: The dimensionless transfer potential E varies with time. Note:

Based on the experimental results, the moisture diffusion coefficients of birch wood at different stages according to the drying benchmark can be obtained. The calculated results are shown in (Table 2).

According to Table 2, the diffusion coefficient varies with changes in moisture content and temperature. Literature review indicates that the moisture diffusion coefficient of wood increases with an increase in initial moisture content. This is because higher moisture content leads to faster moisture diffusion, resulting in a larger diffusion coefficient. As the moisture content decreases, the diffusion coefficient decreases as well. When the temperature increases, it affects the diffusion of moisture in the cell walls. The elevated temperature provides energy to the water molecules, making it easier for them to overcome binding forces. In actual drying processes, combining the moisture content and temperature with the experimentally obtained diffusion coefficient reveals a relatively small range of variation in the diffusion coefficient. This provides a basis for subsequent simulations.

In wood drying simulations, the moisture content of the wood is simulated based on the wood's moisture diffusion coefficient. The variation of the moisture content of the wood over time is depicted in (Figure 3).

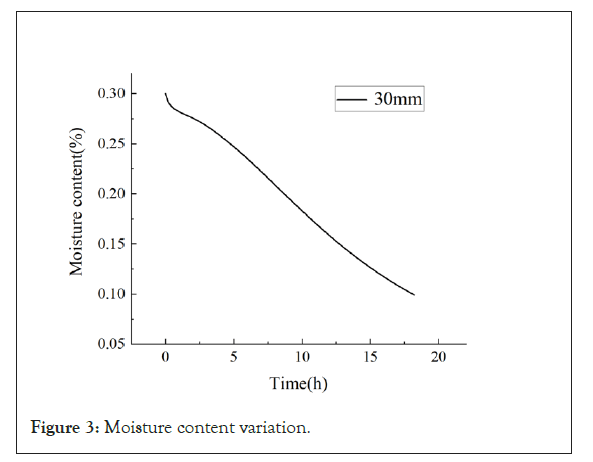
Figure 3: Moisture content variation.

Discussion

During a drying cycle, an if statement is used to modify the drying temperature and diffusion coefficient based on the moisture content in order to achieve accurate simulation. As the moisture content of the wood decreases from 30% to 10%, the duration of the four drying stages gradually increases. This is because as the moisture content decreases, the moisture diffusion coefficient in the wood decreases, leading to an increased drying time. This observation is in accordance with the experimental results. Apart from moisture content, drying temperature is also one of the factors that influence the drying rate [5]. Under the condition of a constant initial moisture content, the moisture diffusion coefficient in wood significantly increases with rising temperature. However, in practical drying processes, the moisture content and temperature mutually influence each other, thereby altering the moisture diffusion coefficient in wood. By cal ibrating the moisture diffusion coefficient and conducting drying simulations, it becomes possible to accurately simulate issues related to excessive drying and insufficient drying in wood drying, which holds significant importance for subsequent wood processing. Additionally, by combining the simulation with the drying benchmark, the optimal temperature, humidity, and airflow conditions can be determined to achieve efficient and uniform wood drying, thus providing a solid theoretical foundation for energy-efficient and environmentally friendly wood drying practices [6-8].

Conclusion

Based on the drying benchmark of birch wood, this study experimentally determined the moisture diffusion coefficients of birch wood under the combined influence of different moisture content and temperature conditions. The obtained moisture diffusion coefficients are as follows: 2.36 × 10^-5 cm²/s, 2.09 × 10^-5 cm²/s, 1.88 × 10-5 cm²/s and 1.63 × 10^-5 cm²/s. The integration of moisture diffusion coefficient calibration experiments and simulations allows for the comprehensive utilization of experimental data and mathematical models. This approach provides a reliable and credible method to calibrate the dimensionless transfer potential of birch wood at different initial moisture contents under various temperature conditions. By employing this method, researchers can gain a better understanding of and predict the behavior of moisture migration in wood, thus offering valuable guidance and references for engineering design and practical applications in related fields.

Declarations

• Both data and materials are true and available.

• The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

• Funding source declaration: The source of funding is Heilongjiang Natural Science Foundation Project (LH2022060).

• Conceived and/or designed the work that led to the submission, acquired data and played an important role in interpreting the results.

Acknowledgements

I would like to express my sincere gratitude to the following individuals and organizations for their support and assistance during the completion of this research work:

First and foremost, I would like to extend my heartfelt appreciation to my supervisor, Professor Zhaoxin Meng, for their invaluable guidance and encouragement throughout the entire research process. Their expertise and experience have had a profound impact on me and have provided significant support both academically and personally.

Furthermore, I am indebted to Heilongjiang Natural Science Foundation Project for providing access to experimental equipment and data support, enabling the smooth progress of my re- search. Their professional expertise and resources have played a crucial role in this study.

Lastly, I express my appreciation to all anonymous reviewers and editors for their valuable suggestions and feedback, which have helped to improve and refine this paper.

In conclusion, I extend my heartfelt thanks to everyone who has lent me assistance and support. Without all of you, this research would not have been possible.

References

1. Hong G, Meng Y, Gao J, Zhang S. CFD numerical simulation technology and its application to wood drying. Wrld For Res. 2017;30(4):47-51.

   [Google Scholar]

2. He X, Wang L. Experimental determination of moisture diffusivity of birch. IOP Conf Series: Earth Envir Sci. 2020;546(4): 042012.

   [Crossref] [Google Scholar]

3. Zheng Z, Liping S. A computational model of wood moisture content and temperature variation during drying process. For Engin. 2014;30(1):49-51.
4. Zhaoxin M. Study on multi-field couping modeling simulation and optimization of wood drying. 2011.
5. Gu C, Yao S, Pan D, Sun S, Guan L, Wu K, et al. Experimental research on the drying characteristics of flexible fibrous biomass fuels in the baffled-rotary cylinder. Energy Fuels. 2019;33(3):2285-2292.

   [Crossref] [Google Scholar]

6. Janjai S, Lamlert N, Intawee P, Mahayothee B, Haewsungcharern M, Bala BK, et al. Finite element simulation of drying of mango. Biosyst Engin. 2008;99(4):523-531.

   [Crossref] [Google Scholar]

7. Perkowski Z, Perkowska JS, Gajda M. Comparison of moisture diffusion coefficients for pine, oak and linden wood. J build phys. 2017;41(2):135-161.

   [Crossref] [Google Scholar]

8. Pan Y, Xian G, Li H. Numerical modeling of moisture diffusion in an unidirectional fiber‐reinforced polymer composite. Polym Compo. 2019;40(1):401-413.

   [Crossref] [Google Scholar]