Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2014) Volume 4, Issue 2
International studies of radon indoors and in workplaces have shown significant radiation dose burden of the general population due to inhalation of radon (222Rn) and its short-lived progeny (218Po,214Pb, 214Bi, 214Po). As far as atmospheric radon concerns, 222Rn, is not necessarily in equilibrium with its short-lived progeny. For this reason, radon’s equilibrium factor F was solved graphically as a function of the track density ratio R=TB/TR, namely of the ratio between the recordings of cup-type and bare CR-39 detectors. TB was computed through special Monte-Carlo codes which were implemented for the calculation of the efficiency of bare CR-39 polymers, regarding their ability in sensing the alpha particles emitted by the decay of radon and its short-lived progeny. For a realistic approach, Monte-Carlo inputs were adjusted according to actual experimental concentration measurements of radon, decay products and F of Greek apartment dwellings. Concentration measurements were further utilized for the calculation of the unattached fraction, fp, in terms of Potential Alpha Energy Concentration (PAEC, defined as the sum of the initial - per volume - energies of all alpha particles emitted due to the decay of radon and its short-lived progeny that are present within a certain amount of air). This was employed for the calculation of F in terms of ratio (A4/A0), where Ai represents the activity concentration of radon (i=0) and 214Po (i=4) respectively. Measured and calculated values of F were plotted versus R. The results were fitted and checked with model’s predictions.
<Radon (222Rn) is a naturally occurring radioactive gas generated by the decay of radium (226Ra) which is present in soil, rocks, building materials and waters [1]. Following the decay of radium, a fraction of radon emanates and migrates through diffusion and convection. After migrating, part of radon escapes to the atmosphere and waters, and, disintegrates to a series of short-lived decay products (progeny) (218Po, 214Bi, 214Pb and 214Po). Outdoor concentrations of radon and progeny are low (in the order of 10 Bq.m-3). On the other hand, indoor concentrations are accumulated, as a result of geological and meteorological parameters, ventilation, heating, water use and building materials [1]. Due to indoor accumulation, radon and progeny are recognised as the most significant natural source of human radiation exposure [1] and the most important cause of lung cancer incidence except for smoking [1].
Radon and its short-lived progeny disintegrate through a- and b-decay. In specific 222Rn undergoes a-decay with λ0=2.093x10-6 s-1, 218Po a-decay with λ1=3,788x10-3 s-1, 214Pb b-decay with λ2=4.234x103 s-1, 214Bi b-decay constant with λ3=5.864x10-4 s-1 and 214Po a-decay with λ4=4,234x103 s-1 [1,2]. In indoor environments 222Rn, is not necessarily in equilibrium with its short-lived progeny and for this reason the equilibrium factor F serves as a fare compromise for identifying the status of equilibrium between parent 222Rn and remaining short-lived progeny [1,2]. Continuous measurement of F is time-consuming and requires active instruments. Hence the time-integration of F prerequisites special apparatus and may not be easily employed in large-scale surveys. For this reason, several researchers investigated combined uses of bare and cup-enclosed Solid State Nuclear Track Detectors (SSNTDs) for long-term estimation of F [2-8]. This paper reviews the theoretical aspects of the topic and formulates an new approximation based Monte-Carlo simulation, actual measurements and related published data. The paper addresses issues of relating recordings of bare CR-39 SSNTDs with those of calibrated cup-type dosimeters
Theoretical aspects
Radon’s equilibrium factor, F, is defined as the ratio of the equilibrium equivalent concentration of radon (Ae) over the actual activity concentration of radon in air (A0), namely [1]:
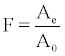 (1)
(1)
Equilibrium equivalent concentration is determined by the following equation [1,9-14]
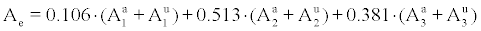 (2)
(2)
and hence
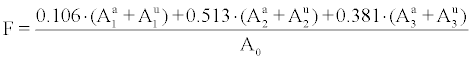 (3)
(3)
Superscripts a and u distinguish the contribution of each one of the two states of radon progeny (attached, unattached), subscripts 1,2 and 3 correspond to 218Po, 214Pb and 214Bi and A0, 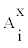 (x=a,u and i=1,2,3) (Bq.m-3) represent measured concentrations of radon and progeny respectively.
(x=a,u and i=1,2,3) (Bq.m-3) represent measured concentrations of radon and progeny respectively.
Assuming radioactive disintegration, ventilation and deposition as the sole processes of removal of radon progeny in ambient air, 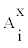 (x=a,u and i=1,2,3) can be calculated as [2,3]:
(x=a,u and i=1,2,3) can be calculated as [2,3]:
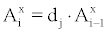 (4)
(4)
Parameter dj reported by Faj and Planninic [3] can be expressed as
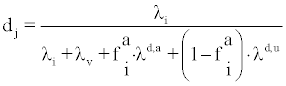 (5)
(5)
Where λv represents the ventilation rate, λid,x (x=a,u and i=1,2,3) is the deposition rate constant of attached and unattached progeny and
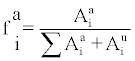 (6)
(6)
is the attached fraction of progeny i. Neglecting the attachment of 214Pb,214Bi and 214Po nuclei, F may be calculated as:
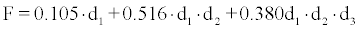 (7)
(7)
Faj and Planninic [3] calculated dj as a function of λv employing the Carnado’s formula. The solution enabled calculation of F as a function of λv, namely F = F (λv). Similar approach has been followed previously as well [3,7,12,13,16,17].
In actual conditions, however, attachment of unattached progeny to aerosol and humidity particles may differ and this affects progeny concentrations 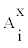 (x=a,u and i=1,2,3). According to recent publications [9,10], the deposition and attachment rate constants of attached and unattached progeny differentiate in high-humidity environments due to peaking of water droplets and for this reason, symbolisation λid,x (x=a,u and i=1,2,3) was adopted. Presuming however only typical lowhumidity ambient room environments under a Jacobian [12,13,15] steady-state with complete mixing, λid,u and λid,a
(x=a,u and i=1,2,3). According to recent publications [9,10], the deposition and attachment rate constants of attached and unattached progeny differentiate in high-humidity environments due to peaking of water droplets and for this reason, symbolisation λid,x (x=a,u and i=1,2,3) was adopted. Presuming however only typical lowhumidity ambient room environments under a Jacobian [12,13,15] steady-state with complete mixing, λid,u and λid,a
can be considered approximately constant for indoor room conditions [3,4,7-9,11]. In such conditions attachment and deposition rates are equal between unattached and attached nuclei and hence, symbolisation λd,x (x=a,u) could be employed. According to Porstendorfer et al. [13] in typical rooms no differences are usually addressed between ambient electrical charged and neutral progeny clusters in attaching to aerosols and and depositing to surfaces. Under this perspective, the deposition rates of attached and unattached progeny to surfaces are equal. Employing symbolisation of Porstendorfer et al. [13] the term 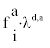 of equation (5) represents the deposition rate of attached nuclei, namely
of equation (5) represents the deposition rate of attached nuclei, namely
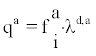 (8)
(8)
Where qa is the symbol for the deposition rate of all attached progeny. Symbolising qu the deposition rate of all unattached progeny it follows from (9) that
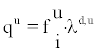 (9)
(9)
Assuming a steady-state Jacobian model and complete mixing, concentrations of attached and unattached nuclei can be calculated then as [13]
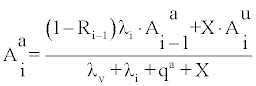 (10)
(10)
and
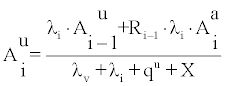 (11)
(11)
Where Ri is the recoil fraction of progeny i, X is the attachment rate to aerosols and i =1,2,3. R1 =0.8 while R2=R3=0 [1]. Employing (10) and (11) in (3), F can be calculated as a function of λv, λd,u, λda and X, namely F = F (λv, λd,u, λda, X). The latter approximation was employed by Eappen et al. [7] upper and lower bounds for F as well as average modelled values and related uncertainties.
It is very important that both approaches for the calculation of Ax (x=a,u and i=1,2,3), namely equation (4) for Faj and Planninic and equations (10),(11) for Eappen et al. [2,3,7] yield to similar final approximations for the most probable relation of modelled values of
F versus measured progeny concentrations 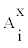 (x=a,u and i=1,2,3). This relationship can be employed for the determination of F versus the recording efficiency between bare and cup-type SSNTDs (R). According to Faj and Planninic (1991) [4] this relationship follows the exponential law
(x=a,u and i=1,2,3). This relationship can be employed for the determination of F versus the recording efficiency between bare and cup-type SSNTDs (R). According to Faj and Planninic (1991) [4] this relationship follows the exponential law
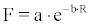 (12)
(12)
where
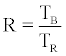 (13)
(13)
And TB , TR are the recorded track density values of bare and cupenclosed SSNTDs. Similar were also the results reported by other investigators [3,4,7,14] Figure 1 presents the best approximations of F versus R according to the model of Faj and Planninic and according to the model of Eappen et al. [7] (Jacobi’s model). Excellent coincidence is observed for all values of R.
Theoretical approach
Let’s assume a twin CR-39 detector system, namely a bare CR-39 SSNTD and another enclosed in a cup. The detector inside the cup records tracks attributable to time integrated 222Rn concentration and the detector outside records tracks due to both 222Rn and its progeny. While radon’s concentration is unequivocally estimated, it is not so direct to estimate the progeny’s equilibrium factor and PAEC from the track density of bare detectors. When the environment predominantly consists of radon and its progeny, a unique relationship as the one of equation (12) can be established between equilibrium factor values and the ratio of the cup to bare detector track densities [3-7,14,16-21].
Lets symbolise by TR and TB the track density values recorded on CR-39 by cup-type and bare detectors respectively. For calibrated CR- 39 cup-type dosimeters, TR will relate linearly to the concentration AO of 222Rn outside the cup. On the other hand, the track density TB of bare CR-39’s will be proportional to the ambient concentration of all a-emitting nuclei, namely to AO of 222Rn, A1 of 218Po and A4 of 214Po. If KR and KB are the sensitivity factors tracks.cm-2 perBq.m-3 of cup-type and bare CR-39 respectively, then
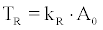 (14)
(14)
and
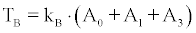 (15)
(15)
Since A3 = A4. Equation (13), according to (14) and (15) can be written as
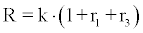 (16)
(16)
where
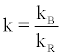 (17)
(17)
is the sensitivity factor ratio, 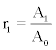 and
and 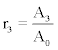 Importantly, equation (17) calculates R from the concentration ratios r1and r3. According to equations (3), (16) and (17), if the concentrations
Importantly, equation (17) calculates R from the concentration ratios r1and r3. According to equations (3), (16) and (17), if the concentrations 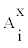 (x=a,u and i=1,2,3) are known from measurements, equilibrium factor
(x=a,u and i=1,2,3) are known from measurements, equilibrium factor 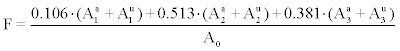 can be calculated from measurement as well as from
can be calculated from measurement as well as from 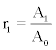 and
and 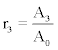 . If additionally the sensitivity factors kB and kR are known then k can be determined, and hence R. In this manner, the relationship between F and R can be established.
. If additionally the sensitivity factors kB and kR are known then k can be determined, and hence R. In this manner, the relationship between F and R can be established.
Experimental approach
In the framework of the NRSF Thalis Project of TEI of Piraeus, Greece, several active radon and progeny measurements have been conducted in Greek dwellings. Numerous measurements were performed with EQF3023 (EQF) of Sarad Instruments Gbhm. This instrument allows continuous 2-hour cycle measurement of radon and progeny nuclei, the latter discriminated for their attached or unattached mode. Radon’s concentration is measured through ionisations produced within a chamber installed inside EQF by the alpha particles emitted during the decay of a radon’s amount that is collected at the beginning of each cycle via 10-minute pumping. Progeny concentration is measured by two semi-conductor detectors at two stages. First, during the first hour of the 2-hour cycle, all alpha activity is collected by the first semiconductor either if this corresponds to unattached or attached progeny. Simultaneously, the second detector collects the unattached progeny nuclei that manage to transmit through a mesh-grid of 50 nm. Then, during the second cycle, the semiconductor detectors are interchanged, while, at this stage, the first remains in contact with a paper filter on which all plated out progeny are also measured. Through alpha-spectrographic techniques and proper mathematical analysis, as stated by the manufacturer’s manual, all activities are determined. From the active database, several actual values of A0 and 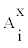 (x=a,u, i=1,2,3) were employed. From these additional value sets were calculated as averages at the 95% confidence interval, under the constraint of employing only partial values of a certain dwelling measurement-set during each calculation. From these actual
(x=a,u, i=1,2,3) were employed. From these additional value sets were calculated as averages at the 95% confidence interval, under the constraint of employing only partial values of a certain dwelling measurement-set during each calculation. From these actual 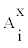 (x=a,u, i=1,2,3) measurement sets, equilibrium factor F values were calculated according to (3). Additionally, to this type of calculation, F was also derived from calculated values of the unattached fraction, fp, in terms of PAEC as
(x=a,u, i=1,2,3) measurement sets, equilibrium factor F values were calculated according to (3). Additionally, to this type of calculation, F was also derived from calculated values of the unattached fraction, fp, in terms of PAEC as 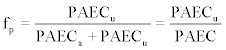 where
where 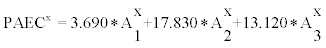 (x=a,u, i=1,2,3). This was employed for the calculation of F in terms of ratio
(x=a,u, i=1,2,3). This was employed for the calculation of F in terms of ratio 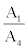 according to Doerschel and Piesch [14] where Ai represents the activity concentration of radon (i=0) and 214Po (i=4) respectively.
according to Doerschel and Piesch [14] where Ai represents the activity concentration of radon (i=0) and 214Po (i=4) respectively.
Passive radon measurements within the Thalis Project are being conducted with a cup-type CR-39 dosimeter which was calibrated previously [15]. This cup-type dosimeter has well-established linear response to radon exposure. The sensitivity factor of this dosimeter has been experimentally defined and found equal to kr = (4.62 ± 0.33) (tracks.cm-2 perBq.m-3.h). From the actual measurements of A0, TR was calculated according to (14).
Track density of bare CR-39 detectors was calculated by means of combining the real measurements of EQF with results derived via Monte-Carlo methods. More specifically, A1 and A3 were calculated from EQF measurements considering that 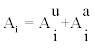 i = 1,3. From these and the corresponding A0 values, the concentration ratios were calculated as
i = 1,3. From these and the corresponding A0 values, the concentration ratios were calculated as 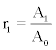 and
and 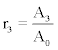 . Since kB is not easily measurable, Monte-Carlo methods were employed for its determination. The following steps were followed:
. Since kB is not easily measurable, Monte-Carlo methods were employed for its determination. The following steps were followed:
1. The distance l travelled by alpha particles prior to hitting CR-39 was calculated versus alpha energy through SRIM2013 for the whole alpha-particle energy range of radon’s decay chain. The relationship
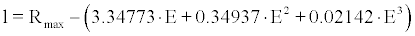 (18)
(18)
was employed where Rmax =4.09cm for alpha-particles originating from 222Rn, Rmax =4.67cm for alpha-particles originating from 218Po and Rmax =6.78cm for alpha-particles originating from 214Po.
2. Random emission points of 222Rn, 218Po and 214Po were generated around CR-39 and their travelling direction vectors were calculated.
3. From the direction vectors of (2), the hit data (l,θh,φh) were calculated.
4. For alpha-particles with l inside an effective volume, incident energy Eh was calculated from the reciprocal of (18) under the constraint θh ≤ θcr.
5. From hit data (Eh,θh,φh) the range and end points in CR-39 were calculated.
6. Steps (1)-(5) were iterated for N0 particles of 222Rn, 218Po and 214Po.
7. From steps (1)-(6) the number of recorded particles of 222Rn, N0rec , of 218Po, N1rec and and of 214Po , N4rec were calculated To estimate realistic values of N0 for 222Rn, 218Po and 214Po (denoted as N0,i) the following equation was employed
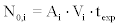 (19)
(19)
where 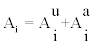 Vi is the sensitive volume’s dimensions, texp is an assumed value for the exposure time (30 days) and i=0,1,4. From (19) and the Monte-Carlo output the recorded particles Nirec, i=0,1,4 were calculated. From Nirec the track density of bare CR-39 detectors was calculated as
Vi is the sensitive volume’s dimensions, texp is an assumed value for the exposure time (30 days) and i=0,1,4. From (19) and the Monte-Carlo output the recorded particles Nirec, i=0,1,4 were calculated. From Nirec the track density of bare CR-39 detectors was calculated as
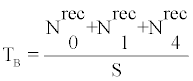 (20)
(20)
Where S is the area of the employed CR-39 detectors, namely 1 cm2.
From (20) the total sensitivity factor kB of bare CR-39 detectors was calculated as
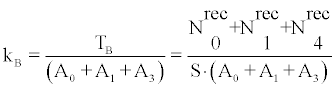 (21)
(21)
Table 1 presents characteristic sets F, R according to the methodology already described. It may be recalled that the F values were calculated from experimental EQF measurements and that the R values were calculated from measurements and calculations.
The relationship between F and R has similarities to that of Figure 2. For this reason the data of Table 1 were fitted to the exponential model (12), namely to F = a.e-b.R Fitting gave a = 0.1663, b= -0.5165 with r2=0.91. These data are in accordance to the published results of Faj and Planninic, Eappen et al. [3,4,7]. It is noted that the latter publication represents a critical review of the subject together with other results. Differences are due to differences in the sensitivity factor of the employed cup-type dosimeters of this study and those of the other studies. Indeed different geometries of cup-type dosimeters induce differentiations in detection efficiency due to alterations (a) in the field that the detectors face; (b) in the distribution of energies and incidence angles of alpha particles that hit the detector’s surface or surfaces; (c) in radon’s entrance properties e.g., diffusion, permeability etc.; (d) other reasons. The relationship between calculated values of F and R indicated non good fit to the exponential model (12) with r2=0.51. This finding strengthens the integrity of the approximation followed in this paper, namely the “semi-empirical” modelling, viz., Monte-Carlo modelling fed with experimental measurements. Accounting the criticism of the method of Doerschel and Piesch [13] from several researchers [5,7,16-21] the fit result of calculated F values verified, more or less, this criticism. No other F -calculation approaches [6,7.14,18,21] were attempted, despite that some of these could provide better estimation of F -values. Nevertheless, the approach of this paper outweighs in one fact; the actual measurements of F. In addition, the overall Monte- Carlo modelling constitutes a new approach to previous simulations [16,18-26], most importantly, by taking into account the latest version of SRIM software, namely SRIM 2013. Apart from the work of Rezaie and Rezaie, et al. [22,23] which also used SRIM, all previous modelling for use of nuclear track detectors in long term estimation of F, followed completely other approximations [17,18] or mathematical-analytical models [16,24,25]. However, despite the different approximations, the findings of this paper could be useful for alternative long-term estimation of F or Monte-Carlo modelling of cup-type, bare detectors or other detector installations. This latter view, namely long-term estimation of F, was the final outcome of this work. Accounting the findings of this work, long-term measurements with CR-39 polymers will be implemented. Further work will simulate LR-115 polymers under similar semi-empirical modelling approach, expecting to implement a multi-sensor assembly of cup-enclosed and bare CR-39 and LR-115 polymers for long-term radon progeny measurements.
| Equilibrium Factor F | Ratio R |
|---|---|
| 0.3384 | 1.5852 |
| 0.3137 | 1.1319 |
| 0.3379 | 1.1273 |
| 0.2562 | 1.0043 |
| 0.2865 | 1.0838 |
| 0.3148 | 1.5200 |
| 0.2540 | 1.0117 |
| 0.2628 | 1.1810 |
| 0.3249 | 1.0240 |
| 0.3137 | 1.0051 |
| 0.2781 | 1.0200 |
| 0.3345 | 1.2846 |
| 0.3957 | 1.4425 |
| 0.3164 | 1.1810 |
| 0.5709 | 2.3939 |
| 0.6748 | 2.7557 |
| 0.7413 | 2.7300 |
Table 1: Characteristic value sets of F, R.
From the data of Table 1, sensitivity factors of bare CR-39 SSNTDs were calculated according to (21). Average kB of this study was found equal to kB = (4.6 ± 0.6)(tracks.cm-2 perBq.m-3.h). This value does not differ significantly from the value of kR. The latter implies from equation (17) that k k ≈1. This finding is very important. Indeed, Faj and Planninic [3,4] assumed equal values for kB and kR. The present study verifies this result. Similar was also the outcomes of Eappen et al. [9]. Related publications gave also comparable results [5,6]. All these findings could be explained by the fact that CR-39 registers alpha particles from radon and progeny identical either if enclosed in a cup or bare. Observed track density differences are attributable only to the fact that cup type CR-39 dosimeters are proportional to radon concentration only, while bare CR-39 SSNTDs register proportional to the concentrations of all alpha-emitters. Future work will employ other expressions of F namely those that take into account the the unattached fraction in terms of PAEC.
This study reported a newly developed Monte-Carlo simulation tool for modelling the CR-39 SSNTDs efficiency. Simulation combined Monte-Carlo techniques, experimental data and the latest version of SRIM (SRIM2013) software program group. This “semi-empirical” simulation perspective constitutes a completely new approach in SSNTD modelling. Modelling rendered calculation of sensitivity of CR-39 detectors based on energy and angular distributions of alpha-particles emitted by the decay of radon and progeny. The relationship between equilibrium factor F and recorded track density values ratio (of bare and cup-enclosed SSNTDs respectively), R, was additionally calculated through measurements and calculations. The sensitivity of bare CR-39 detectors was calculated equal to kB = (4.6 ± 0.6)(tracks.cm-2 perBq.m- 3.h). This value is not significantly different from the corresponding sensitivity factor kR of the cup-type dosimeters employed in this work. The ratio of for kB and kR was found approximately one, namely k ≈1 . This finding is considered as very important since it is verifies the results the similar studies. In addition, it also verifies the integrity of Monte-Carlo simulation and the overall mathematical approximations.
This research has been co-financed by the European Union (European Social Fund – ESF) and Greek national funds through the Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF) - Research Funding Program: THALES Investing in knowledge society through the European Social Fund.