Forest Research: Open Access
Open Access
ISSN: 2168-9776
+44 1300 500008
ISSN: 2168-9776
+44 1300 500008
Research Article - (2014) Volume 3, Issue 4
Ash dieback, caused by the ascomycete Hymenoscyphus fraxineus, is rapidly expanding over large geographical areas in Europe. A myriad of factors influence pest invasions and long-term establishment, i.e., species’ life stage, the availability of suitable hosts and the suitability of the environment. This paper examines the principal environmental features that characterise naturally infected zones in order to forecast the potential distribution of the pathogen within the ranges of European ash species by means of Species Distribution Modelling and an ensemble forecasting technique. Furthermore, a network analysis permitted dispersal dynamics to be included in order to obtain realistic risk predictions for the natural spread. The multi-modelling procedure allowed the most endangered regions to be identified as the central and eastern Alps, Baltic States, southern Finland and the area encompassing Slovakia and southern Poland, whereas most marginal regions of the study area appeared less suitable for the natural establishment and spread of the disease. Statistical model predictions were highly correlated with abundant summer precipitation, high soil moisture and low air temperature. A novel approach to the ensemble forecasting technique in epidemiological modelling of plant pathogens is suggested as a tool to aid the survey of this infectious disease. Moreover, the final potential distribution maps may promote discussions about the control of the disease and the risks associated in the trade or movement of ash species.
<Keywords: Ash dieback; Hymenoscyphus pseudoalbidus; Chalara fraxinea; Fraxinus; Species distribution models; Epidemiology
GDD: Growing Degree Days; TSS: True Skill Statistic; AUC: Area Under The Curve; ROC: Receiver Operating Characteristic; GLM: Generalised Linear Model; LOG: Logistic Regression Model; SVM: Support Vector Machine Model; MLP: Multilayer Perceptron Artificial Neural Network; CHAID: Chi- Squared Automatic Interaction Detector Classification Tree; WA: Weighted Average
Ash trees in Europe are threatened by a major disease caused by the ascomycete Hymenoscyphus fraxineus (T. Kowalski) Baral, Queloz, Hosoya, comb. nov. (basionym Chalara fraxinea T. Kowalski, synonym Hymenoscyphus pseudoalbidus Queloz et al.) [1-4], most likely introduced from East Asia [5]. The disease was first observed on Fraxinus excelsior L. in northeastern Poland in the 1990s [6], but the pathogen was identified as the primary causal agent of ash dieback in 2006 [1]. Symptoms were also observed in both European (F. angustifolia Vahl. and, only under artificial conditions, F. ornus L.) and introduced ash species (F. nigra Marsh., F. pennsylvanica Marsh., F. americana L. and F. mandschurica Rupr.) [7-10].
Wind-dispersed ascospores, produced during the summer in apothecia on the previous year’s leaf remnants in the litter, can penetrate and infect ash leaves via appressoria [10-12]. The symptoms that subsequently develop include necrotic leaf spots: wilting of leaves and young shoots: premature shedding of leaves: crown dieback: and necrotic bark lesions extending to the phloem, paratracheal parenchyma and parenchymatic rays below the bark [13,14].
At the present time, fully effective measures to control the disease are still lacking [15-18]. Due to its rapid spread in the majority of European countries [1,11,19], H. fraxineus was added to the EPPO Alert List in 2007 but was later deleted because sufficient alert was considered to have been given [20].
Predicting the spread of emerging infectious diseases is fundamental for forecasting potential ecological consequences and designing control strategies [21-26], and mathematical models have long been widely used for agricultural and forest diseases [21,22,27-30], in particular, to predict the spread of parasites and pests [31-35] or the risk of infection in pest-free areas [36-38]. Among those extensively employed, Species Distribution Models (SDMs) can identify statistical or logical functions linking species’ occurrences to a series of predictors, and project these relationships onto a geographical space, allowing range dynamics to be estimated and suitability maps defined [39]. Infact, the SDM approach is based on the concept of Grinnellian niche as a constraint to the potential distribution of species and can easily be implemented using ecological and evolutionary assumptions (i.e., selecting the most causal environmental predictors or determining a restricted set of competing models in multi-model inference) [40,41].
Some environmental characteristics connected to a pathogen’s biology are known or hypothesised from field observations and laboratory experimental proofs. In terms of temperature requirements, H. fraxineus can be classified as a mesophile [42], considering that most isolates in pure culture show their maximal growth rate at approximately 20°C and cease to develop at approximately 30°C [43]. However, in ash tissues, the fungus exhibits less tolerance to heat [16]. On the other side, the pathogen is considered a cold-tolerant organism because of the ability of producing necroses during the winter and phialides at low temperature [43,44]. The asexual stage of the pathogen is most likely strongly associated with the pseudosclerotial plates that it produces on infected rachises [10] and that allow the fungus to overwinter [12,13]. The main hypothesis for subsequent fertilisation is proposed by Gross et al. [45] and supposes that conidiospores (spermatia), readily produced on the petiole in autumn, could be mediated by free water till the fusion with an ascogonium [13,45]. Ascospores of H. fraxineus, produced in the leaf litter by apothecia, are windborne and secure the dispersal and spread of the pathogen [45,46]. They are produced in abundance during several months in late spring and summer and are considered drought sensitive [10]. Furthermore, Husson et al. [47] found a positive correlation between soil moisture and the percentage of affected collar circumference caused by H. fraxineus in northeastern France. Additionally, Gross et al. [45] supposed that moist soil conditions could favour the survival of the pathogen on ash rachises in the litter and apothecia production. The discharge of spore has a peak in the morning [11], most likely to prevent spore desiccation and to facilitate germination [11,42]. Moreover, depending on altitude and related climatic conditions, the pathogen’s apothecia first appear at the end of May, June or early July, subsequently with a different duration of dispersal [48]: in addition, the genetic intrapopulation variability of H. fraxineus is highly dependent on elevation, and, together, on the number of days with snow cover [49].
The artificial long-distance movement of infected ash commodities is known to have contributed to the spread of the disease [3,10], so that a Plant Health Order was introduced in Great Britain to restrict imports of ash plants and seeds to those originating in pest-free areas, despite the confirmed presence of the pathogen in a number of sites in the country [50], but little is known about the natural spread potential of H. fraxineus when considering habitat suitability. According to official reports [11,20], not all the distribution ranges of F. excelsior and F. angustifolia are affected yet. By means of an ensemble forecasting technique, resulting from a combination of nine distribution models, the main objective of this study was to examine the potential natural distribution of the parasite in European and neighbouring regions according to the geographical distribution of its hosts and to the main environmental features of the sites in which the natural presence of the disease was reported. Secondly, the natural spread of the pathogen was simulated, in order to consider the role of airborne spores in dispersal. In this perspective, nurseries and recent plantations that may be associated with the movement of infected plants for planting [3,10,51,52] were intentionally excluded.
Study area
The extension of the study area was based on the natural distribution maps of the three indigenous European ash species known to be susceptible to the parasite under natural conditions [8,53]. F. excelsior and F. angustifolia distribution maps were obtained from EUFORGEN and FRAXIGEN official databases with previous authorisation [54,55], imported into Quantum GIS software (QGIS Development Team) [56], and then converted into a single georeferenced shapefile corresponding to the study area. On the contrary, F. ornus was not included in the modelling because this species can develop limited necrotic lesions after artificial inoculation but appears to be resistant under field conditions [3].
Pathogen’s presence
The greatest number of scientific reports of H. fraxineus were collected in a data-set by means of a wide bibliographic study (used keywords “Hymenoscyphus pseudoalbidus”, “Chalara fraxinea”, “ash dieback”, “dieback” or “decline of Fraxinus excelsior” or “European ash” or” common ash” or “Fraxinus angustifolia” or “ narrow-leafed ash”, and the combinations of these in all languages of the countries included in the study area: time frame for the research 01/06/2013- 30/09/2013: publications had to be scientific papers referring to records of the disease that were spatially included in the study area: 27 final papers considered) [11,47,56-78] (authors, unpublished data). As the movement of asymptomatic, infected plants for planting is responsible for the artificial spread of the disease [3,10], reports in plantations younger than 3 years (the minimum time for confirmation that the site could be suitable for the pathogen) [79] and in nurseries were excluded from processing (16 records excluded). In this way, 252 sites with symptomatic ashes within the study area were considered (Figure 1).
This type of data can show patchy spatial coverage and some regions where the detected ash dieback had a greater recorded density than others, which was most likely derived from different sampling methods [80,81]. Moreover, these types of records are often closer to roads, rivers, coasts, towns and cities or concentrated in areas that are of more interest to collectors [74] than they would be if the survey effort were completely random [82-85]. To correct for this spatial bias, the resolution of the final study area was fixed in a 0.5° x 0.5° regular grid considering the spatial accuracy and precision of species records, according to Dungan et al. [86]. Presence points were then intersected with this grid, thereby reducing the number of presences to 177 patches containing at least one infected point [87].
Environmental variables
The predictor set included 12 environmental variables. For every predictor with a temporal scale, a subset January 1992 - December 2013 [11] was considered and monthly averages were computed in Raster Map Calculator in GRASS GIS (Grass Development Team, S. Michele all’Adige, Italy) [88]. The variables were selected for their relevance to the pathogen’s biology and current main hypotheses on its life cycle, as reported in the introduction section. Precipitation, frequency of days with frost and monthly mean temperature maps were obtained from available Climatic Research Unit (CRU) time-series datasets [89-90], and the Growing Degree Days (GDD) computation was performed with a temperature threshold of -10°C [42,91]. Maximum, mean and minimum monthly temperature at a height of 2 m, surface temperature, soil moisture (0-10 cm depth) and runoff were obtained from NCEP/ NCAR Reanalysis 2 [92,93]. Snow cover and elevation maps were acquired from MODIS/Terra Snow Cover Monthly Dataset [94] and from SRTM 90 m Digital Elevation Data [95], respectively. Wind speed and direction were obtained from NCEP/NCAR Reanalysis 2 [92,93] but, after computing monthly averages in the considered temporal range, final maps showed no spatial pattern in the study area [56,96], also for the months more suitable for spores’ dispersal [11]. Therefore, these predictors were discarded from further analyses.
To avoid multi-collinearity [97] and model over-fitting [98], the 122 environmental predictors (10 monthly predictors plus digital elevation data and GDD November-March, according to Table 1) were subjected to a collinearity control, based on the Pearson correlation between predictors [99] (Table 1). In this way and according to Peers et al. [100], when the correlation between two variables was statistically significant for r>0.85 and p<0.0001 (IBM SPSS Statistics software v. 22, International Business Machines Corp., New York, USA) [101], the most adequate predictor was selected using information about the fungal biology [22,102,103]. According to Merow et al. [104], this approach eliminates correlation and allows more parsimonious and interpretable models. Finally, the resulting maps were overlaid with the grid’s study area while considering the average values in the centroids (the centre points of defined areas [105]).
| Chosen predictor | Monthly averages calculation | Variables correlated (r>0.85, p<0.0001) and discarded |
|---|---|---|
| Digital elevation data | ||
| Mean temperature | * | Maximum, minimum and mean temperature at a height of 2 m; Skin temperature |
| Frost day frequency | * | Snow cover |
| Precipitation | * | |
| GDD November-March | Maximum, minimum and mean temperature at a height of 2 m; Skin temperature | |
| Soil moisture (0-10 cm depth) | * | Runoff |
Table 1: Shows the variables used for model building and the discarded predictors after the collinearity control based on the Pearson correlation (r). Stars indicate the selected predictors for which a monthly average was computed.
Pre-processing of data
The modelling was directly trained in the whole study area as no other regions with similar environmental ranges, hosts and disease’s presence have been detected to date [20], nor could a subplot represent all the considered climatic zones [106,107]. Moreover, taking into account the unavailability of absence data for the pathogen [108], background data (also referred as “pseudoabsences”) were included in model construction [109-111]. Pseudoabsences were generated randomly, reducing the number of background points to three times the number of presences, according to Wisz and Guisan [112] and Barbet- Massin et al. [111]. The resulting data were then separated in three partitions in a split-sample approach (IBM SPSS Statistics software v. 22, International Business Machines Corp., New York, USA) [101,113]: training (65%, comprising 115 presences and 345 pseudoabsences) and validation (15%, with 27 presences and 80 pseudoabsences) sets were used in the construction and calibration of the individual models with the control of overfitting [114], respectively. The remaining data (test set, 20%, with 35 presences and 106 pseudoabsences) were used for comparing models [115].
Species distribution modelling procedures
In accordance with Elith et al. [109] and Guisan and Thuiller [41], more than one modelling algorithm, both classical and novel, was adopted. Methods were grouped on the basis of algorithm class into the following five categories: 1) Regression based models, 2) Classification Trees [116] and, within the machine learning community, 3) Artificial Neural Networks (ANN) [117], 4) Support Vector Machine (SVM) [118] and 5) Maxent [119,120]. The chosen regression-based models were backward stepwise logistic regression (with only main effect or with first order interactions: LOG) and a Generalised Linear Model (GLM), considering a binomial distribution, previously used extensively in species’ distribution studies [121-127]. CHAID (Chisquared Automatic Interaction Detector), belonging to the category “Classification tree”, was chosen in order to take advantage of multiple splitting pathways for each grid’s node [128-129] and two models were built, considering both boosting and bagging (bootstrap aggregation) procedures [130]. Boosting and bagging procedures were also performed within the Artificial Neural Networks (ANN) Multilayer Perceptron category (MLP), which is considered more powerful than multiple regression models when modelling nonlinear relationships [121,131]. The last two machine learning algorithms used were the Support Vector Machine (SVM), recently introduced in a species distribution context [132,133], and Maxent (Maximum Entropy Model), estimating the target probability distribution by finding the probability distribution of maximum entropy [119-120,129]. Among the five categories of model construction, 1 to 4 were built in IBM SPSS Statistics software (v. 22, International Business Machines Corp., New York, USA) [101], and the SVM algorithm was implemented in LibSVM library (v. 3.17) [134], while the Maxent model was produced in Maxent software (v 3.3.3k)[119-120]. For each type of model, respective statistical parameters were calibrated in order to optimise the resulting sensitivity. Multiple runs (maximum = 50) for each model gave the distribution probability in each cell, which generated a final output with a mean predictive cell value ranging from 0 to 1.
Evaluation statistics
To evaluate the performances of the nine models, the predicted values were compared with the test set by means of contingency tables (also called a confusion matrix) [135] obtained with IBM SPSS Statistics software (v. 22, International Business Machines Corp., New York, USA) and considering the conventional threshold of 0.5 [136]: predicted relative probabilities ≥ 0.5 were classified as presence, whereas relative probabilities <0.5 were classified as absence. The classical measures derived from the confusion matrix and calculated in Microsoft Excel (v. 2007, Microsoft Corporation, Redmond, USA) [137] were a) overall accuracy, b) specificity, c) sensitivity, d) Kohen’s Kappa statistic and e) the True Skill Statistic (TSS) (Table 2) [136,138]. The Area Under the Curve (AUC) of the receiver operating characteristic (ROC) [139-142] was obtained in IBM SPSS Statistics software (v. 22, International Business Machines Corp., New York, USA), using the obtained measures as the probability that one score associated to a random presence site is higher than the probability of a random pseudoabsence site [143]. The Fpb index, specifically relying on presences and pseudoabsences [135], was then calculated from the contingency tables. In this way, the regions where the pathogen’s establishment is possible but did not occur or was not yet detected, were not considered. For each category of model construction, only those that performed the highest Fpb measures were used to generate relative suitability surfaces in the study area and a qualitative comparison in Quantum GIS (QGIS Development Team) [56] was performed. A quantitative comparison was performed on the basis of the percentages of agreement among the predicted probabilities of selected models that were calculated on the whole dataset considering the conventional threshold of 0.5 between presence and pseudoabsence [136].
| Measure | Formula |
|---|---|
| Overall accuracy | 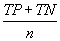 |
| Sensitivity | 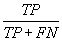 |
| Specificity | 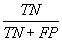 |
| Kappa statistic | 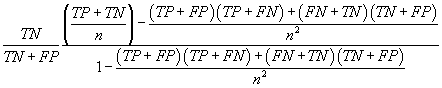 |
| TSS | 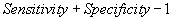 |
| Fpb | 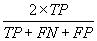 |
Table 2: Parameters used in the evaluation of individual models and the weighted average consensus model. n-Total Number of Cases; TN-True Negative; FP-False Positive; TP-True Positive; FN-False Negative [135].
The weighted average consensus model and spatially realistic probability
Considering that the nine models gave partially different probability maps but performed very well in the comparison with the test set, rather than selecting just one as definitive, their prediction outputs were combined using a consensus modelling framework procedure [144- 146]. Furthermore, this approach can enable more robust decisionmaking in the face of uncertainty, in particular in a conservation planning context [147]. Therefore, a Weighted Average (WA) was calculated on the previous evaluation of the selected modelling techniques but because pseudoabsences cannot be considered as confirmed H. fraxineus absences, instead of using conventional AUC values as weights [145,148], the new measure of Fpb was exploited:
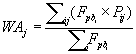
with P representing the predicted relative suitability [149] of the single model i for each grid cell j. The performance of the new WA consensus model was assessed with the same statistics and test set used for the individual models described above.
Because the natural spread of a pathogen is an intrinsically spatial process [150], the spatially explicit model for H. fraxineus in the study area was produced to identify possible suitable areas not reachable with a natural spread process, using the following procedure. According to a precautionary approach, the patches resulting as suitable for the pathogen or useful as transitional zones were selected in Quantum GIS (QGIS Development Team) [56] from the potential map obtained from the ensemble modelling technique [145,148]. This operation was made through a binary transformation and considered the threshold maximising the True Skill Statistic [111,151]. A script in R [152] was written ad hoc to generate a network [153-155] among neighbour polygons with a distance lower than 1.3° (approximately 120 km) and with a safety factor of one (two times the maximum spread distance indicated in the literature, given that the natural spread rate of H. fraxineus can reach 60 km/year [10,156]). R code for the construction of the spatially explicit model is included as part of the Supplementary Information (Appendix S1: Map S2 for execution). The spread of the pathogen from the presence points in the network was then simulated in R (100 iterations over time). In this way, the final prediction excluded the areas potentially prone to natural spread in the WA consensus model, but not the regions gradually reachable from presence areas.
The contributions of each environmental variable to the construction of the models used in the WA consensus procedure obtained from the software were merged in a single relative importance value (OI, Overall Importance) to achieve a more readable result. This arrangement was achieved by computing a weighted average (Microsoft Excel v. 2007, Microsoft Corporation, Redmond, USA) [136] using the Fpb value associated with each individual model, similarly to the construction of the WA consensus model:
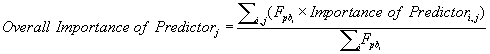
where j represents the predictor and i the individual model.
Extension of the study area
The shapefile corresponding to the study area included most of Europe plus neighbouring countries, from a northern limit in southern Scandinavia to some parts of north-western Africa and Anatolia, from Ireland and Portugal to western Russia and northern Iran (Figure 1).
Chosen predictors
The collinearity test based on the Pearson correlation allowed the number of predictors to be reduced from 122 to 50, as reported in Table 1. In particular, the maximum and minimum temperature at a height of 2 m, snow cover and runoff were discarded from further analyses. From the intersection of the maps with the grid, 4576 background samples were obtained and then reduced to 531 to allow model building.
Model fits and comparison
During model building, each type of algorithm was optimised and the best final set parameters are reported as part of the Supplementary Information in Appendix S3. The relative efficacy of the models on the test set was evaluated by comparing contingency tables (Figure 2, see Appendix S4 for a deepen explanation) and a series of parameters (Table 3). Among the models, SVM and MLP built with boosting or bagging procedures and Maxent achieved the highest measures of overall accuracy, sensitivity, Kappa statistic and TSS. In the comparison of the algorithms on the basis of the ROC curve (Figure 3), the SVM and the two MLP models were the best performing in predictive accuracy. This result was confirmed by the respective AUC values (AUC>0.9: Table 3). Considering specificity and Fpb, the values covered a greater range, indicating that LOG with first order interactions and CHAID bagging models performed significantly worse than the others in the same categories. As a result, the models selected for the WA consensus model for each category of construction on the basis of Fpb measures were GLM, SVM, CHAID built with boosting procedure, Artificial Neural Network MLP with boosting procedure, and Maxent. The WA consensus model often achieved higher performances on the basis of the evaluation parameters than the single models used for its construction.
| Model | Overall accuracy | Specificity | Sensitivity | Kappa statistic | TSS | AUC | Fpb |
|---|---|---|---|---|---|---|---|
| GLM | 0.81 | 0.83 | 0.71 | 0.49 | 0.54 | 0.87 | 0.88 |
| LOG, main effects | 0.81 | 0.88 | 0.58 | 0.45 | 0.46 | 0.88 | 0.80 |
| LOG, 1° order interactions | 0.55 | 0.52 | 0.65 | 0.11 | 0.17 | 0.56 | 0.47 |
| SVM | 0.89 | 0.91 | 0.81 | 0.69 | 0.72 | 0.92 | 1.22 |
| MLP, boosting | 0.90 | 0.94 | 0.74 | 0.69 | 0.68 | 0.92 | 1.21 |
| MLP, bagging | 0.84 | 0.88 | 0.71 | 0.56 | 0.59 | 0.92 | 0.98 |
| CHAID, boosting | 0.81 | 0.88 | 0.67 | 0.49 | 0.54 | 0.85 | 0.88 |
| CHAID, bagging | 0.81 | 0.88 | 0.55 | 0.43 | 0.43 | 0.83 | 0.76 |
| Maxent | 0.85 | 0.90 | 0.65 | 0.55 | 0.55 | 0.90 | 0.95 |
| WA consensus model | 0.90 | 0.93 | 0.77 | 0.70 | 0.70 | 0.94 | 1.23 |
Performances were computed on the test set considering overall accuracy, specificity, sensitivity, Kappa statistic, True Skill Statistic (TSS), the area under the curve (AUC) of the Receiver Operating Characteristic (ROC) and Fpb (Table 2). The best four values for each parameter are italicised; the bold values indicate the best model for each category (according to those presented in the Materials and Methods section) on the basis of Fpb measures. Abbreviations: GLM: Generalised Linear Model; LOG: Logistic Regression Model; SVM: Support Vector Machine Model; MLP: Multilayer Perceptron Artificial Neural Network; CHAID: Chi-squared Automatic Interaction Detector Classification Tree; WA: Weighted Average.
Table 3: Performances of the individual models and the weighted average consensus model.
Figure 2: Mosaic plots for every single model and weighted average (WA) consensus model. Mosaic plots were obtained from the contingency tables used to compare predicted probabilities with the test set (threshold of 0.5 [136]). In each plot, “s = 0” and “s = 1” stand for “pseudoabsence” and site with symptomatic ashes in the reference set (test set); “p = 0” and “p = 1” indicate predicted the unsuitability and suitability scenario by the single model. The size of the box obtained from the combination of every “p” with “s” is proportional to the number of cases for each contingency table case. In particular, the blue, black, green and red boxes indicate the proportion of “true negative”, “false positive”, “true positive” and “false negative”, respectively (sensu Li and Guo [135]). Abbreviations: GLM, Generalised Linear Model; LOG, Logistic Regression Model; SVM, Support Vector Machine Model; MLP, Multilayer Perceptron Artificial Neural Network; CHAID, Chi-squared Automatic Interaction Detector Model; WA, weighted average.
Figure 3: ROC curves for the individual models and for the WA consensus model. Sensitivity is plotted against the corresponding proportion of false positives (1-specificity), at various threshold settings. Abbreviations: GLM, Generalised Linear Model; LOG, Logistic Regression Model; SVM, Support Vector Machine Model; MLP, Multilayer Perceptron Artificial Neural Network; CHAID, Chi-squared Automatic Interaction Detector Classification Tree; WA, weighted average
The projections of the selected models in the QGIS software were visually different both in predicted extent and in the levels of the relative probabilities (Figure 4). In particular, the GLM forecast a wider potential area, with eastern extremes in the Moscow region (Figure 4A). In the SVM, the potential area was more restricted and had higher associated relative probabilities (Figure 4B). A similar result was obtained for the MLP, but with more irregular and fragmented areas (Figure 4C) in addition to the CHAID regression tree model (Figure 4D). The spatial pattern associated with the Maxent model was completely different and consisted of a smoother and larger potential distribution with a low relative suitability of presence, which also reached some southern zones in the study area (Figure 4E).
Figure 4: Estimated spatial distribution of H. fraxineus in Europe according to the individual models. According to the legend, different colours represent different levels of predicted relative suitability. A, Generalised Linear Model (GLM). B, Support Vector Machine (SVM). C, Artificial Neural Networks Multilayer Perceptron (MLP), with boosting building. D, Chi-squared Automatic Interaction Detector (CHAID) Classification Tree, with boosting procedure. E, Maxent.
Although the models tended to differ in the magnitude of predicted relative probabilities, agreement was reached by all the models in highlighting the central, northern and eastern Alps, Baltic States, southern Finland and the zone including Slovakia and southern Poland as more suitable areas for the pathogen as potential scenarios.
Considering the quantitative comparison among these models on the basis of predicted relative probabilities in the whole dataset after applying the 0.5 threshold, the percentage of agreement varied from 86.3% to 93.4%, whereas the accordance of the models with the WA consensus model achieved higher percentages (89.4% - 96.7%: Table 4).
| Model | GLM | SVM | MLP, boosting | CHAID, boosting | Maxent | WA consensus model |
|---|---|---|---|---|---|---|
| GLM | - | 88.4 | 88.8 | 86.3 | 87.9 | 89.4 |
| SVM | 88.4 | - | 93.4 | 91.7 | 89.9 | 96.3 |
| MLP, boosting | 88.8 | 93.4 | - | 91.6 | 90.0 | 96.7 |
| CHAID, boosting | 86.3 | 91.7 | 91.6 | - | 89.1 | 94.4 |
| Maxent | 87.9 | 89.9 | 90.0 | 89.1 | - | 91.5 |
| WA consensus model | 89.4 | 96.3 | 96.7 | 94.4 | 91.5 | - |
The table reports the agreement among relative probabilities predicted by the best models for each category chosen according to the Fpb measures reported in Table 3. Predicted relative probabilities are rounded to 0 (pseudoabsence) or 1 (presence) using the conventional threshold of 0.5 [136] before percentages’ computation and comparison.
Table 4: Percentages of agreement in relative probabilities predicted by selected individual models and the weighted average consensus model on the whole dataset.
WA consensus and spatially realistic models
The potential map of H. fraxineus drawn from the WA consensus model appeared to be an intermediate result in comparison with previous models (Figure 5A): the areas at major risk of spread (p>0.7), such as the central and eastern Alps, Austria, Switzerland, eastern France, central Ukraine, southern and northern Poland, northeastern Germany, southern Sweden and Finland, central Denmark, southeastern England and the Baltic States, were confirmed and connected by areas of low-medium relative probabilities (0.25
Figure 5: Estimated spatial distribution of H. fraxineus in Europe according to the final models. According to the legend, different colours represent different levels of predicted relative suitability. A, WA consensus model. Ensemble values were calculated using a weighted summation approach where predictions from individual models were combined on the basis of individual model valuation. B, Spatially explicit model, obtained from the network analysis.
The final map obtained from the network analysis (threshold obtained for TSS maximisation 0.25) represented the spatially explicit distribution for H. fraxineus (Figure 5B), with the predicted distribution overlapping the greater part of the WA consensus map but with some patches, such as in the Pyrenees and Caucasus, which were not considered, being not gradually reachable from the potential area in Central Europe.
Environmental variables associated with the natural spread of H. fraxineus
Important variables in creating model fits were consistent in all models except for Maxent. Of the 50 predictors, the most important ones (OI ≥ 2, OI = Overall Importance) are reported in Table 5. Precipitation in July and August were the two most important variables, with OI values of 7.2 and 12.1, respectively. Precipitation in June and soil water content in August were also relatively strong predictors correlated with the occurrence of ash dieback (OI = 5.7 and 5.6), while temperature in July and August played a moderate role (OI = 3.9 and 3.2). In general, apart from elevation (OI = 2), the other predictors represented averages during the summer months. In particular, when compared to the average values of the whole study area, the presence of H. fraxineus was associated with a low mean temperature between June and September (16.6 °C), abundant summer precipitation (> 80 mm) and higher soil moisture content (> 30%).
| Environmental predictor | Overall importance | Mean value in presence dataset |
|---|---|---|
| Elevation | 2.0 | 359.2 m |
| Mean temperature, January | 2.3 | -0.5 °C |
| Mean temperature, June | 2.3 | 16.8 °C |
| Mean temperature, July | 3.9 | 18.1 °C |
| Mean temperature, August | 3.2 | 17.9 °C |
| Mean temperature, September | 2.8 | 13.7 °C |
| Frost day frequency December | 2.6 | 21.7 °C |
| GDD November-March | 2.0 | 1743.1 °C |
| Precipitation, May | 2.5 | 77.8 mm |
| Precipitation, June | 5.7 | 91.4 mm |
| Precipitation, July | 7.2 | 100.4 mm |
| Precipitation August | 12.1 | 93.8 mm |
| Precipitation, September | 2.0 | 82.1 mm |
| Soil moisture, March | 2.2 | 0.35 |
| Soil moisture, July | 3.3 | 0.31 |
| Soil moisture, August | 5.6 | 0.30 |
Variables with OI>2 are shown; predictors with OI>6 are in bold, italicised text indicates the variables with 3
Table 5: Overall Importance (OI) of environmental predictors included in model building.
Due to the rapid spread of H. fraxineus in Europe reported in recent years [10,20], this study was performed to provide a spatial prediction of the vulnerability of indigenous ash tree species in Europe, considering the distribution of hosts and the main environmental factors associated with naturally infected sites.
Among the nine algorithms compared, the Support Vector Machine (SVM), Artificial Neural Network Multilayer Perceptron (MLP) with boosting procedure and Maxent models achieved the highest measures of specificity, Kappa statistic, Area Under the Curve (AUC) and Fpb, demonstrating that they fit the test set better than the other models, which allows projections of observed patterns into independent situations and minimises over-fitting of data [157]. Sensitivity, an essential measure in models with presences and pseudoabsences, was significantly higher in the Generalised Linear Model (GLM), SVM and MLP Artificial Neural Network models. The generally higher performance of machine-learning methods, most likely due to peculiar advantages, such as robust parameter estimates, model structure learned from data and easy fitting of complex interactions, in spite of considering the use of pseudoabsences in models evaluation [110], was therefore confirmed [158].
Among the performance measures considered, prominence was given to the Fpb statistic. This accuracy assessment was recently proposed by Li and Guo [135] for presence-only modelling, to specifically consider presences and pseudoabsences instead of true absences in the confusion matrix [159]. Given that the performance of such models with regard to Fpb were quite robust, but that their predictive maps partially differed in the extension and magnitude of relative suitability of the pathogen’s presence, in accordance with Stohlgren et al. [160], the consensus ensemble forecast was calculated as the weighted average of the best models, highlighting the areas of agreement among models as expected and thereby minimising the weakness of any given algorithm [144,147-148]. The resulting model, highlighting the areas suitable for the pathogen, generally outperformed any single algorithm based on the evaluation parameters (mainly Kappa statistic, AUC and Fpb) and suggested a potential distribution map with higher risk for the central and eastern Alps, Baltic States, southern Finland and Sweden Slovakia and southern Poland. This approach can enable more robust decision-making in the face of uncertainty [147], however, as suggested by Elith et al. [161], caution should be taken in selecting models for an ensemble forecast. An understanding of the data, single models and predictions should not be underestimated, especially in the case of a climate change context.
Species Distribution Models (SDMs) and ensemble forecasting lead to interesting conclusions on the ecological appropriateness of some areas to the potential pathogenic spread of H. fraxineus [40]. To take into account the dispersal limitation [162] and obtain a more realistic projection, a novel approach to the network analysis was implemented, which considered the potential map obtained from the ensemble modelling technique and the points where the disease presence can be considered as derived from a natural infection. In this way, most of the edging areas of the F. excelsior chorological map resulted as unsuitable for a natural spread in the final scenario (i.e., western Ireland, part of France and northern Spain, all the southern areas in central Italy, the Balkans and northern Turkey and western areas in Russia, the Caucasus and Iran). The reported consensus ensemble forecast potential distribution map may therefore indicate the areas where the trade of ash species should be under particular control. In any event, caution should be taken in transferring predicted results from a wider scale to a more local scale [163,164]. The disease in Europe most likely originated from a single introduction event of the pathogen of at least two individuals with compatible mating types and was first observed in the early 1990s in Poland [165], although there is an hypothesis of the introduction of the pathogen together with the importation of F. mandschurica to Estonia [166]. The computed network analysis based on current presence points aimed to deliver realistic predictions, so the potential distribution in the case that the disease originated in others regions was not implemented.
The expected spread to F. angustifolia largely resulted as low, except for some areas in northern Italy, Slovenia, Croatia, Bosnia- Herzegovina and Romania, confirming the hypothesis of Gross et al. [10], who reported that the epidemic rate in Europe is slowing down, the sill of a sigmoid function of spatial growth against time has been reached. Similar studies on invasive pest modelling suggest that environmental conditions may serve as a constraint limiting the spread in respect to the hosts’ distribution. For instance, Podger et al. [167] considered the establishment of Phytophthora cinnamomi in potential areas with annual mean temperature < 7.5°C and annual mean rainfall < 600 mm as unlikely. Moreover, Koch and Smith [168] estimated the potential spread of non-native Xyleborus glabratus in the southeastern U.S. and concluded that climatic conditions could prevent the spread from coastal plain to eastern interior forests.
As a result of the modelling, precipitation, soil moisture and air temperature were shown to be significantly more influential than other predictors in model building of the potential distribution of H. fraxineus. In particular, the species distribution appeared to be highly dependent on abundant rainfall and high soil moisture content in the summer months, confirming the hypothesis of more intense ash dieback near water courses or in high soil moisture sites [169,170] and supporting the hypothesis of Gross et al. [45] about the importance of free water for the fertilisation of the H. fraxineus anamorph on petioles. Summer mean temperatures were also relevant for model construction of the pathogen niche, consistent with available information on the species [16]. In an ecological and biological interpretation, the temperature ranges highlighted by the models could be necessary for apothecia production, known to occur from May to October, with a peak in July, with a minimum temperature of 1.1°C and optimum temperature of 22°C [11,171]. Considering the low January mean temperature in areas where the species was present (-0.5°C), various studies indicate that the fungus can develop within the plants over the winter, causing necrosis [19], and the mycelium tolerates freezing at -20°C for at least two months and can even survive-70°C for at least one month [10]. In addition, conidial sporulation is favoured in vitro by temperatures between 5 and 15°C [43] and was observed in nature in autumn on ash rachises in the ground litter [53].
Modelling was directly trained on the entire study area in order to cover all the environmental gradients in the distributions of F. excelsior and F. angustifolia and to avoid underestimating climatic factors in delimiting species’ distribution [106]. Moreover, attention must be paid in considering relative suitability predictions of the models, because of the possible lack of equilibrium, which is typical of an invasive pathogen not yet reaching its full potential distribution [161]. For this reason, further reports of ash dieback over time, including the probable original Asian distribution [5,172], could be easily taken into account to enlarge the boundaries of the Grinnellian niche (closer to equilibrium, according to Pulliam [173-175]). The availability of a wider time series, including data on ash dieback severity and host abundance, will allow the consideration of the spread dynamics of the disease in the context of different landscapes and in a climate change scenario [175-177]. More detailed mathematical analyses are in progress, to identify the specific high performance components in the machine learning models able to describe the biological and ecological complex interactions involved in the expression of the disease.
This work was financially supported by the Land Environment Resources and Health (L.E.R.H.) doctoral course (http://intra.tesaf.unipd.it/school/lerh. asp: University of Padova) and by the University of Padova (“ex-60% 2012”). The authors thank Dr. G. Frigimelica and D. Jurc for their kind cooperation, the FRAXIGEN project and the EUFORGEN programme for the license to use the ash distribution maps, and the members of the FPS COST Action FP1103 (Fraxback).