H: Hydrophobic Vector; D: Pseudo Electric Dipole Moment Vector.

The tendency of proteins to self-assemble is probably one of the most basic but albeit least known phenomena of the life of cells. Health, or conversely, a large spectrum of diseases depends on whether these assemblies or lack thereof take place correctly or not. Under the physico-chemical point of view, protein self-assembling processes can be considered analogous to the processes of protein folding. In the same manner in which a protein in the process of folding descends to reach its proper energy minimum, assembling proteins descend in their energy well to reach their minimum functional energy. Nevertheless self-assembling processes have their own characteristics. For example, a conformational change in a protein may result in a pathological process of self-assembling impairing the protein in the performance of its original function [1-3].

The present study considers hydrophobic and electrostatic interactions as being the most important factors for self-assembling [4-7] and it is a continuation of other previous works [8,9] where we propose some simple biophysical rules, common to all self-assembling processes. In our “biological membrane model”, we postulate that molecules possessing a hydrophobic moment tend to assemble in such a way as to align their hydrophobic moments. This is what actually takes place in a lipid bilayer, where phospholipids possessing a hydrophobic moment in the direction along the molecule, tend to align (Figure 1). However, in the same way a layer of phospholipids must be associated to another layer in the opposite direction (in polar media), a given protein assembly needs to associate to another assembly in the opposite direction so the total hydrophobic moment of the ensemble cancels out. Similarly, formation of spherical phospholipid micelles has an analogous counterpart in protein assemblies when they form spherical structures (i.e. virus capsids). In such cases the total hydrophobic moment, H_tot, is zero. In both the cases, lipid bilayers or spherical micelles, the tendency of the phospholipids is to associate trying to hide their hydrophobic elements. In this article our “biological membrane model” will be referred to simply as “membrane model”.

Figure 1: Hydrophobic moment vector.
a) Schematic representation of a single phospholipid. The hydrophobic moment 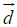(green arrow) is defined as the vector obtained from multiplying the hydrophobicity of the phospholipid times the vector 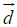(black arrow) joining the hydrophobic centroid (“+”, somewhere in the tail) and the hydrophilic centroid (“–“, in the polar head), (see Methods).
b) Schematics of a lipid bilayer showing the total hydrophobic vectors of each layer (green arrows). In a lipid bilayer the total hydrophobic moment is zero for any given area of the membrane.

Nevertheless, it is not common to find protein associations that physically resemble membranes. On the contrary, protein associations have a great variety of aspects due to various facts. They are larger molecules than phospholipids and consequently steric constraints may impose important limitations in the way they accommodate binding to each other. Besides, the fact of possessing electrostatic charges also imposes an important interaction between them. Electrostatic forces may modulate hydrophobic interactions and this relationship between them is what gives rise to such a variety of final structures when proteins self-assemble. A remarkable example is shown in those proteins that, when assembled, the particular compromise between electrostatic and hydrophobic interactions make the ensemble fold on itself, comprising a finite number of elements, as mentioned above. In a previous work [8], we showed that in those closed systems, the total hydrophobic moment and electric dipole moment are zero (or marginal), no matter how large or complex the system may become. This is not surprising, since these closed structures end up being very stable and symmetrical.

In open structures, the subject of the present study, the singular and relative interaction between hydrophobic and electrostatic forces do not allow the closure of the assembly on itself but allows unlimited growth as new elements are added to the complex. These structures do not lack symmetry, no matter how H_tot and D_tot evolve [10].

Materials

A set of 19 open self-assembly systems have been used for this study. In choosing these systems we have tried to be as comprehensive as possible but trying to avoid those described previously [8]. The PDB identifiers of these systems are: 3G37, 4APW, 2HIL, 2MJZ, 5JZC, 2NLQ, 5I55, 2M4J, 5O3L, 3J89, 5JCG, 2OM3, 3J2U, 5SYC, 3ZEE, 3NGK, 2DI4, 4CKP and 4AA7. These systems were classified in four groups according to the type of structures they show (Shown in Results). The choice of these particular systems obeys to the need of showing as much variability as possible, both in sizes of the basic components but specially in the shapes of the resulting complexes, as well as the final distributions of the vectors involved. Detailed 3D structures of these complexes with their vectors can be visualized by downloading the individual files from the server http://wallace.uab.es/Self-assembling/. These files can be opened using UCSF Chimera, version 1.12 for Windows or alpha for Macintosh users.

Methods

The characterization of the interactions involved in the processes of self- assembling, namely hydrophobic and electrostatic interactions was done by means of the calculation of their respective moment vectors [8,9].

The hydrophobic moment vector, H has been defined and used in several ways [11-15]. Here we define it by using both hydrophobic and hydrophilic (polar) centroids and the Eisenberg hydrophobicity scale for amino acids [11,12]. Since virtually no protein is "neutral" in hydrophobicity terms, that is, its total hydrophobicity differs from its total hydrophobicity, the hydrophobic moment vector of a protein is defined here as the product of its total hydrophobicity h+, times the position vector joining both hydrophobic and hydrophilic centroids (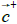and):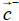

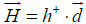
Where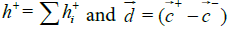

Since the Eisenberg hydrophobicity scale used in this work has arbitrary units, it has been normalized. Consequently, hydrophobic moments units are also arbitrary and are designed as ‘‘rhu’’ (relative hydrophobic units) for comparison purposes.

In an analogous way, most proteins normally are not electrically neutral, so the regular definition of electric dipole moment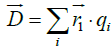cannot apply in our case. Instead, we use the definition of a pseudo electric dipole moment defined in an analogous way as the hydrophobic moment: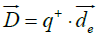

Where 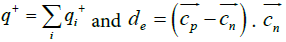and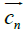 are the positive and negative electric centroids. This pseudo-electric dipole moment is referred as "dipole moment", D, in the present work. This definition of electric dipole moment coincides with the true electric dipole moment when the total charge of the protein is zero. In this paper, D will be expressed in Debyes.

In the present work a new parameter is used to characterize a given protein or assembly of proteins, H/D, that is, the ratio of the modules of hydrophobic and electric dipole moments. This parameter has no units but in relative terms it provides a means of comparing the relative strengths of both hydrophobic and electrostatic interactions among proteins and when a given protein undergoes a self-assembly process.

Following the characteristics and similarities of assemblies and affinities we have grouped these open complexes in four types: 1. Linear growth; 2. Amyloid & Stacking; 3. Helicoidal Growth & Microtubules and 4. Higher order assemblies.

Linear growth

The most frequent mode of association of this type (but not exclusive) begins with a dimer or trimer that serves as a nucleus, followed by elongation. In this nucleus, the individual H vectors tend to align parallel to each other, whereas D vectors adopt relative orientations tending to optimize their interactions, that is, either in a counter- parallel (attraction) or perpendicularly (near-zero interaction). It must be noted that in these interactions the relative values of H/D of the growing complexes are relatively small, revealing that the electrostatic interaction is important (at least compared to other types of associations). As the assembly proceeds, more elements are being added to the complex in the form of filaments, normally with a tendency to helicity. This helicity probably surges from the need to accommodate the individual D vectors to configurations of lowest energy possible and also allowing for steric constraints. Thus, in these growths, total H (H_tot) increases indefinitely, since the individual H vector are often considerably aligned. The major component of D vectors lie on the plane perpendicular to the axis of growth, with a smaller component in the direction of growth. This component also increases as the filament grows.

Conspicuous examples of this type of assembly are shown in Figure 2 for proteins with PDB identifiers: 3G37, 4APW, 2HIL, 2MJZ and 5JZC.

Figure 2: Linear growth.
a) Actin, PDBid: 3G37 [16]. The basic element of assembly is monomeric actin. As monomers get incorporated onto the filament, their individual D vectors alternate their orientations and thus optimize their electrostatic attraction. The resultant vector H_tot increases linearly in the direction of growth as monomers are added to the filament. The analysis of this complex qualitatively corroborates what was described in our previous work for actin PDBid:1M8Q [8]. H/D value of monomers is around 8. As the filament growth H/D values increase to values nearing 50 (with 9 elements). Bluish arrows: H vectors; red arrows: D vector. Green and yellow arrows: H_tot and D_tot (of the 9 elelements). For a 3D visualization using UCSD Chimera, visit http://wallace.uab.es/Self-assembling/ (see Methods).
b) Actin, PDBid: 4APW [17]. The basic element for growth is monomeric prokaryotic actin. This actin comes from Colstridium Tetani and its monomers show a significant difference with those of eukaryotic actin. Also, the vector distribution is different from the former case since filaments tend to align with each other in opposed polarities, as confirmed by the distribution of vectors. Contrary to the eukaryotic case, H and D vectors are better aligned, although their H/D indices are four times smaller (around 1.6 vs. 6.3), while H values are of about the same order of magnitude of those in the eukaryotic case, suggesting a stronger role of electrostatic interactions and favoring the direct counter alignment of filaments. Color codes for the arrows as in a).
c) Pilus, PDBid: 2HIL [18]. These growths are the constituents of pili. The basic element for growth here is a homotetramer in which the four individual H vectors are aligned in a slanted disposition along the axis of growth. Projections of the H vectors on the plane perpendicular to the growth axis cancel each other out. Components along the axis add up in its direction. It can also be seen that the D vectors are basically projected on the plane perpendicular to the growth axis with relatively small projection on this axis. The value of H/D ≈ 50 for both monomers and polymer indicates the preponderance of hydrophobic interactions over those electrostatic. It is reported [18] that there certain counter parallel interactions among these pili.
d) M13 Bacteriophage Capsid, PDBid: 2MJZ [19]. A homopentamer of α−helices is the basic element of assembly. The growth proceeds by a partial insertionof the pentamer in the next pentamer and so on. The resulting structure serves as a capsid for DNA in M13 bacteriophage. The aspect reminds that of 2HIL but does not grow slanted although pentamers in one layer are slightly rotated in respect to those of the next layer. The same considerations made above can be made here, except for the fact that D vectors are rather aligned with H vectors along the axis of growth. Consequently, both H_tot and D_tot increase linearly with the number of elements of the growth. H/D ≈ 3.2 in monomers, pentamers and whole assembly, again indicating relative importance of electrostatic interactions. In the Morag et al. report [19] no external interactions with other analogous assemblies are mentioned, but it must be kept in mind that this structure is meant to hold a DNA molecule with which it must maintain it own interactions. Same color code as in a), b) and c). H_tot and D_tot arrows have not been drawn for clarity.
e) Presynaptic RAD51 filament, PDBid: 5JZC [20]. A 331 amino acids monomer is the unit for this linear association that serves as a helical encasing for ss-DNA. The way in which the assembly proceeds is by increasing H_tot (individual H vectors lie close to the axis of growth) whereas individual D vectors run almos perpendicular to the axis, except for a small perpendicular component. The H/D values, 2 for monomers and 13 for the assembly suggest a rather hydrophobic driven association.

Amyloid & stacking assembly

This assembly modality is characteristic but not exclusive of amyloid assembly.

In its most typical cases, proteins (or peptides) orient their H vectors parallel to each other due to a very intense interaction since they are subjected to relatively small steric constraints. And as is required in our membrane model, an analogous assembly in the opposite direction compensates each association. This is the most general case that includes all amyloid complexes. There are some exceptions such as the microtubule PDBid 3J89 in which its assembly is not compensated by a similar one with its H_tot oriented in the opposite direction.

As indicated above these assemblies are mostly driven by hydrophobic interactions as indicated by H/D values above 30 or higher. It is pertinent to note here that small deviations of H_tot (and also D_tot) from the axis of growth result in helicoidal assemblies, as can be seen in many amyloid formations. In the present work three typical examples of amyloid self-assembly and two examples of microtubules are presented. Other amyloids have been described in a former paper [8]. Figure 3 analyzes typical stacking assemblies: 2LNQ, 5I55, 2M4J, 5O3L, 3J89, and 5JCG.

Figure 3: Amyloid & stacking assembly.
a. Amyloid β-peptide (Aβ), PDBid: 2LNQ, [21]. The basic assembly unit of this assembly is peptide QKLVFFAENVGSNKGAIIGLMVGGVV. This is one of the most conspicuous examples of amyloid growth. These peptides form a stack by aligning their H vectors. Each stack is counter-aligned with another in such a way that their H_tot end up in opposite directions. Note that the D vectors perpendicular to the direction of growth tend to adopt a relative orientation at roughly 90º with each other. Both H_tot and D_tot have a perpendicular increase, suggesting the possibility of forming 2D structures. Typical H/D values are in the 27 – 33 range.
b. Staphylococcus aureus PSMa3 amyloid, PDBid: 5I55, [22]. The basic unit of this growth is peptide EFVAKLFKFFKDLLGKFLGNN. Another clear example of pure “membrane model” in which the filament grows as two opposing layers. Index H/D goes from ≈ 13 for individual peptides to values <2 for the assembly, suggesting a growing role of electrostatic interactions.
c. “Iowa’’ A Fibril, PDBid: 2M4J, [23]. This peptide forms a trimer, which serves as the growing base for this assembly. The trimer itself is formed by three peptides of composition: DEAFRHDSGYEVHHQKLVFFAEDVGSNKGAIIGLMVGGVV. The H and D vectors in the trimer accommodate each other at a 120º of relative orientation and the growth takes place by stacking trimers due to the residual component of H in the direction of stacking. Whether this growth of H_tot gets compensated by another in the opposite direction is not known, but it is conceivable that the close distance between trimers favors the direct alignment of the H vectors of the stacked individual peptides.
d. Tau filaments, PDBid: 5O3L, [24]. The basic element of stacking is a protofilament of 76 amino acids. This is one of the most clear effects of stacking following the "membrane" effect. In this particular case the individual D vectors are in opposition making a net contribution to their attraction and thus suggesting this amyloid assembly must be very stable. H/D index goes from 4.25 of monomers to almost 9.0 in the assembly.
e. Helical Nanotubes PDBid: 3J89, [25]. In this case the basic element for growth is a tetramer arranged as a closed assembly by itself. The component of the total H vector in the plane of the tetramer ("horizontal" plane) is zero but leaves a component perpendicular to the plane ("vertical" component). Also the component of D in the "vertical" plane is near zero. Not surprisingly the H/D index goes from 19 monomers to 28 in the complex. The near vertical component of H is responsible for the stacking. The fact that it is not exactly vertical causes the tetramers to slightly rotate around the axis of growth. As can be seen this is a case that could also be included in the preceding section.
f. Human Peroxiredoxin 3, PDBid: 5JCG, [26]. This structure is a microtubule formed by stacked rings that serve as basic elements of growth. Its peculiarity is that each ring (a hexamer) possesses its H vector in the plane of the ring and a very small D vector (H/D ≈ 25 to 37). This fact drives the rings to stack the rings in parallel arrays. Small differences in the locations of the hydrophobic centroids of the six components of each ring provokes a small asymmetry that gives rise to this vector H within the plane of the hexamer. Authors in [26] attribute the completion of the stacking of the rings to molecular crowding, probably by rejecting polar environments.

Helicoidal growth and microtubules

This is probably the most complex and sophisticated type of self-assembly. On one hand, it involves the formation of very complex structures. On the other hand the elements for assembly are either large or complex proteins or they are small assemblies themselves. The main features of this type of assembly, mostly electrostatic interactions and exacting steric restrictions, are also shared by most closed virus capsids [8].

A common feature of self-assembling shared by these systems is determined by the fact that besides the proposed hydrophobic interaction forcing the individual H vectors to align according to the “membrane model”, the complexity of the structure and the importance of the individual D vectors, prevent a perfect alignment of the basic elements, forcing the assembly to adopt curvatures and slanted lateral stacking, ending up in a helical conformation.

The result is a variety of helical microtubules, as a consequence of the complexity of these systems, in which small and sometimes subtle variations in the basic elements of the assembly may result in very different structures. Figure 4 analyzes four helical microtubule assemblies: 2OM3, 3J2U, 5SYC, and 3ZEE.

Figure 4: Helicoidal growth and microtubules.
a. Tobacco Mosaic Virus, PDBid: 2OM3, [27]. This case may be considered as the typical microtubule construct. The basic element of assembly is a monomer. Individual H vectors tend to align following the membrane model but the mutual interactions of the D vectors prevent a perfect alignment as new elements are incorporated into the structure. Steric limitations also contribute to the adoption of a curvature by the structure. If such curvature contains a sufficient number of elements the most probable is that the circle does not close but rather form a coil. H/D index increases from 18 (monomer) to 60 (50 elements) suggesting that the building of the structure is driven mostly by hydrophobic forces. Blue arrows: H vectors; red arrows: D vectors. The relative scale of H and D vectors have been changed for better visualization.
b. Tubulin-kinesin microtubule PDBid: 3J2U, [28]. The basic elements in this structure are closed assemblies themselves: two tubulin heterodimers are linked by means of a kinesin-13 molecule. What makes this assembly one of the most singular self-assembly systems highlighting the versatility and ductility of hydrophobic interactions among amino acids is the variable interaction between H and D vectors among the amino acids that get incorporated into the microtubule. When one of these elements is added to the microtubule, a difference is observed between the H vectors in respect to the D vectors. D vectors do not change the direction in relation of the structure of the incorporated element. Consequently, as these elements get incorporated, the direction of D vectors change so their projections on the plane perpendicular to the growth show circular symmetry and the resultant D on this plane is near zero. This is in contrast with the behavior of the individual H vectors whose direction always point in the same direction regardless their position in the microtubule. When projected on the plane perpendicular to the direction of growth, they all have the same direction, resulting in a net H_tot vector oblique to the microtubule. This behavior is due to small changes taking place in each of the basic elements of growth (two tubulin dimers linked with kinesin, see Discussion). Subtle changes in the positions of hydrophobic and hydrophilic centroids may give raise to different orientations in each element. No biological function is attributed to this fact so far, although this particular orientation of H_tot of the microtubule suggests the need of a particular orientation with the structures with which it interacts.
c. Tubulin microtubule, PDBid: 5SYC, [29]. The growth of this microtubule is formed by the tubulin heterodimer as the basic element. H vectors of the dimers are accommodated in a slanted form. When projected on the meridional plane, both H and D vectors add up to zero on a whole turn of the microtubule. The components of both H and D vectors on the axis of growth increase with the number of elements in the complex. It is presumable that molecules that act as microtubule stabilizers (taxane-site binders taxol, peloruside and zampanolide) may be contributing to the increase of the hydrophobic moment of the complex since they are also hydrophobic molecules by themselves. As shown in case b), the increase in D may be related to the interaction with nucleotides associated to this structure. Values of H/D are in the 4-5 range.
d. Par-3 N-Terminal Domain, PDBid: 3ZEE, [30]. The basic element of assembling in this helical growth is a monomer. This is a good visual example of both H and D vectors opposing each other. Alignment of H vectors would also imply alignment of D vectors, which result in a repulsive interaction. The relative orientation of these vectors of two consecutive monomers is a compromise between both interactions, preventing a perfect alignment. To the contrary, it implies the appearance of slant and bend of the structure as the assembly proceeds.

Higher order assemblies

There are many instances of very complex assemblies, which could be considered as “assemblies of assemblies”. They certainly comply with the same rules set by the membrane model. Some of these assemblies have been designed artificially and constitute a source of very good examples of 2D and 3D of assembled systems. In some of the example cases described above, it has been shown that the basic element of assembly is a hexamer. In order to form higher order assemblies, hexamers seem to be very suitable elementary unit (although not exclusive). It is worth noting here that in the set of interactions holding the system together, it is frequent to see the partial vectors (both H and D) that are part of the basic element of assembly may be interacting with those of neighboring elements. In such cases, one can find alignment of the H vectors as well as counter alignment of adjacent D vectors, contributing to the stability of the whole system. Figure 5 shows PDB systems 3NGK, 2DI4, 4CKP and 4AA7 as examples of these assemblies of assemblies.

Figure 5: Higher order structures.
a), b) Shell of the Pdu Microcompartment, PDBid: 3NGK, [31].
a) This assembly is is based on a closed hexamer in which individual H vectors have components both on the plane of the hexamer and perpendicular to the hexamer. Components on the plane add up to a null vector. Components perpendicular to the hexamer plane add up to a sizable resultant H vector. This strong component of one hexamer makes it join another hexamer in the opposite direction, as expected from the membrane model.
b) In addition, each set of two opposing hexamers can interact laterally with other six hexamers electrostatically since they try to accommodate opposing dipole moments (encircled red arrows) in the maximum attractive force.
c), d). Cytosolic Region of ATP-Dependent Protease FtsH, PDBid: 2DI4, [32,33]. In this case, it is the alignment of each H_tot (purple arrows) of the hexamers what causes the 2D growth of the system. This configuration leaves the plane components of the H vectors (green, blue and orange arrows) in a 120º mesh ([33]). Red arrows are D vectors. It is not reported though that such layers are stacked in opposite directions as predicted by the membrane model.
e), f). Procentriole assembly, PDBid: 4CKP, [33,34]. According to these authors, this ring interacts with others both by stacking and by lateral association. This assembly highlights the mutual interaction of H and D vectors within a ring and with those of rings located laterally. Also with those above and below. The result is a very regular 3-dimensional network of vectors at 120º from each other as a result of attractive and repulsive interactions of all these vectors.
g), h). Acetyltransferase domain of GlmU, PDBid: 4AA7 [33,36]. Another higher-order assembly case is presented with this trimer that is able to assemble with others on a plane. It should be noted the alternation of polarities in the adjacent trimers. In this case it is very easy to counter-align both the individual H and D vectors, resulting in what should be a very stable structure. It should be noted as a common feature in these cases, in which 2D structures are formed, that the constituting elements of these networks suffer certain loss of identity since parts of their constituents interact with significative strength with parts of neighbouring elements.

One of the examples analyzed above, microtubule PDBid: 3J2U, brings up an important issue for the definition and use of hydrophobic moment vectors. The electric dipole moment has a very well defined entity, derived from the general theory of electromagnetism, in spite of being used here as a quasi- or pseudo-definition. It is easy to develop an intuition of the electric dipole moment derived from the existence of two types of electric charges. The definition of hydrophobic moment is being made here in analogy with the electric dipole moment, since it is based on the existence of a scale of hydrophobicities among amino acids. However, H vectors are much more nuanced because the 20 amino acids adopt values in a more continuous scale for their hydrophobicities (both positive and negative), whereas the electrostatic case has only two possible values (one positive, one negative). As a consequence, it should be no surprise that the H vector of a protein is more sensitive than the D vector to small spatial variations of the amino acids. This is particularly notorious in microtubule 3J2U.

Figure 6 shows the superposition of the 16 elements of a whole turn of the microtubule, each composed of two tubulin heterodimers linked with a kinesin. It shows how small differences in the locations of the hydrophobic and hydrophilic centroids give raise to a cone of possible different orientations of the corresponding H vectors. By contrast, the D vectors show virtually no changes and lie in the same direction. This raises the suggestion that this higher spatial sensitivity of H vectors over that of D vectors may have a significant biological role. This fact, on the other hand, has the disadvantage that small artificial changes in the composition or position of the hydrophobic amino acids can introduce errors in measurements and behaviors of the H vectors. This fact should be borne in mind when analysis of this kind is being carried out.

Figure 6: Superposition of the 16 elements comprising one turn of 3J2U. Front and side view of all the 16 elements (two tubulin heterodimers linked with a kinesin), comprising a turn of the microtubule. This superposition was done by using the SPDBViewer Magic Fit function (Swiss Institute of Bioinformatics). Purple arrows are H vectors. Red arrows are D vectors. Note that individual H vectors are regularly spread over a 360º arc whereas D vectors are all superposed on a thick quasi-single arrow.

There are examples where changes in the environment can affect significantly the characteristics of both H and D vectors and thus implying that alternative structures may appear in different situations. Such is the case of the Tobacco Mosaic Virus coat. TMV coat can appear as a helical tubule (as seen above in Figure 4a) or as a stacked four-layer aggregate (PDBid: 1EI7) depending on the pH of the medium [16-37] and thus, its electric characteristics. Our model shows that it is just a matter of the relative angle that the D vectors of their basic element (dimers) of assembly form: 60º in the stacking case and 27º in the helical case. The latter case constitutes a more unstable situation and thus less probability for closed symmetric circular structure, bearing in mind that the closer to 0º for two adjacent D vectors, the more repulsion among them.

This analysis shows the universal need of proteins to self-assemble into a configuration in which their hydrophobic moments are aligned. The presence of electric dipole moments in proteins modulate or modify this tendency and cause assemblies to produce a great variety of shapes and sizes in the complexes. However, the first question to be asked in this study is: since H_tot generally increases indefinitely with n (number of elements in the assembly), how does this fit in the model’s main hypothesis, according to which a given assembly should be joined by a similar one in an opposition configuration to make H_tot cancel out?

In those cases where the molecules involved are relatively simple or small, as is the case of amyloid peptides, it is clear that another given layer joins in and the total hydrophobic moment cancels out. In other cases (i.e. PDBid: 4APW), grown filaments may interact between themselves in opposite polarities (shown for example [17]). But what about those more complex protein assemblies in which the total hydrophobic moment is not canceled by a similar one opposing it? We postulate that in such cases the assemblies are meant to interact with a great variety of systems: nucleic acids, cell walls, other different self-assemblies, organelles, etc. In such cases interactions are probably driven by the need to align hydrophobic moments, as well as to accommodate electric interactions. At this point, each individual case must be studied separately.

The idea of using the both vectors, hydrophobic moment and electric dipole moment in these types of studies, highlight the advantage and simplicity of our model. The picture is that of a general physical principle that drives proteins together to the appropriate mutual orientation where local interactions of shorter range (i.e. hydrogen bonds) do the binding. The process can be viewed as similar to protein folding where a protein folds following a path towards its energy minimum. In the case of self- assembling, the process relies on physical principles and not on details of protein-protein interactions. Consequently, monomers do not have to explore the whole spectrum of binding possibilities to the assembly but just follow the physical principle to those configurations that have been brought by the combination of their H and D interactions towards their energy minimum.

Moreover, this is a pertinent question that rises when considering the comparison of similar built assemblies (of any of the four types) but with quite different vector distributions. Consider for example the cases of 5JCG and 4CKP. These structures are both rings composed in turn by several monomers and showing remarkable circular symmetry. In both cases the membrane model works in a given direction or mode but is very different in each case. Why does the membrane model not work in the same way in both systems? At the present moment we don’t have a definite answer and this fact suggests that the model is not complete; other effects may need to be taken into account. For example, different kinetic paths can drive different assemblies to end up with similar aspects but with different vector distributions. It is worth mentioning here the great versatility that configurations in the form of hexamers show along different assemblies, especially in those giving rise to 2D systems.

Also, a more specific doctrine describing the direct interaction of the H and D vectors would help to better understand the assembled configurations and it would also make predictions possible and reliable. For the moment, the only parameter we are able to use, H/D can only give a discrete idea of the relative strength (and importance) of both forces in both the single elements of assembly and in the final assembly.

This work was supported by Grants BIO2013-48704-R and BFU2013-50176- EXP from the Ministerio de Economía y Competitividad of Spain, by the Centre de Referència de R+D de Biotecnologia de la Generalitat de Catalunya and from the Comisión Coordinadora del Interior de Uruguay. We thank Mr. Ramón Mozo- Strother for revising the English text.