Sloshing describes the free surface oscillations of a fluid in a partially filled tank. For slosh, the liquid must have a free surface, thus posing a dynamic fluid structure interaction problem. This motion of fluid plays a major role in the cargo slosh in ship, spacecraft, rocket tanks, transportation of liquid and oil storage tanks, water oscillations in storage tanks due to Earthquakes and in reactors of boiling water. The behavior of excitation mainly depends on the frequency, shape and motion of the fluid inside the tank [1]. Liquid sloshing in storage containers is due to Earthquakes is of great importance which causes unavoidable problems and failure of the systems.

Fuel sloshing in drop tank or external auxiliary fuel storage tank of aircraft may adversely affect the structural integrity of the drop tank and may even lead to its complete failure. These oscillations result from lateral and longitudinal displacements or angular motions of the aircraft [2]. It is to be noted that fuel tanks should be designed to carry fuel without any sort of leakage and should possess necessary strength for combined action of different loads and stresses. The drop tank’s centre of gravity should not be altered because of motion of the fluid due adverse effects of flutter and aerodynamic characteristics of aircraft. Classical storage tanks are gasoline tankers and some of missiles rocket storage tanks of horizontal cylindrical shape, sloshing modes in these tanks generated along the axis of the cylinder [2]. In satellites and in some launch vehicles spherical storage tanks are used because of their high volume to weight ratio [3,4]. Toroidal tanks are of different types which are mainly preferred in some spacecraft and launch vehicles because they can fit around engines and some different parts, in boiling nuclear reactors these toroidal tanks act as supporting pools for condensation of steam released [5]. All the aircraft fuel tanks must last the aircraft life.

The sloshing effect in liquid propellants usually interacts with elastic vehicle structural dynamics and control system dynamics or coupled together [6]. The oscillating frequencies are always nearer to rigid body frequencies than the elastic body frequencies. The control of such dynamic behavior is accomplished either by implementation of baffle plates inside the tanks or by modifying the tank geometry itself or by introducing flexible baffle plates for damping the sloshing [7,8].

In space vehicle storage tanks (for missile under thrust), the lateral sloshing is the severe case, hence to avoid that truncated - cone type ring baffles are usually preferred [9,10]. Hence for the design of fuel tank, it is necessary to estimate sloshing loads generated on the fuel tank. Due to the complex nature of theoretical approaches used for solving such Fluid Structure Interaction (FSI) problems, the use of numerical technique becomes essential.

The sloshing method applied initially to 3D rigid rectangular tank which is 1.008 m long, 0.196 m wide, 0.300 m height and has thickness of 0.03 m [11].

Modeling of a typical aircraft drop tank is carried out based on the optimization study. To reduce the aircraft drag especially wave drag Figure 1. Finess ratio of the drop tank should be high. From the Sears-Haack equation [12,13] shape of drop tank has been evaluated by considering the cylinder circular area and is given by the equation 1.

Figure 1: Dimension and initial condition of the rectangular tank.

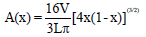
Where, A is cross-sectional area of Sears Haack body, V is volume, L is length and x is the ratio of the distance from the nose to the whole body length. From the above formulation, the maximum length and diameter of the drop tank are optimized to their maximum extent using iteration process for high subsonic flow condition. The dimensions obtained are 4.395 m length and 0.64 m diameter, and dimension also reduced the wave drag formation in the total drag [14]. The dimension of drop tank is shown in Figure 2.

Figure 2: Geometry of a typical aircraft drop tank.

In order to reduce the sloshing effects inside the drop tank, vertical, circular baffle plates are placed inside in it and have three holes. Furthermore, the drop tank is modeled with two baffle plates to observe the effects of sloshing. These two vertical baffle plates are positioned at center of the drop tank separated by 750mm. as shown in the Figure 3.

Figure 3: Different parts of drop tank.

Computational Fluid Dynamics (CFD) analysis is a numerical method based on Finite Volume (FV) technique. It solves for conservation of mass, momentum and energy using continuity, momentum and energy equations respectively [15]. The sloshing basically deals with two immiscible fluids (water and air), it is solved using multiphase Volume of Fluid (VOF) model using ANSYS FLUENTTM to capture the interface of two fluids. The standard k-ε turbulence model [16] has been used for all the computations. The transient simulation has been carried out using explicit time stepping method with a time step size of 0.01 ms up to 0.5 s to maintain numerical stability, to avoid divergence of the solution and to control global Courant number under 250.

Rectangular tank

The fine mesh is generated on rigid rectangular tank and this tank is filled with 60% of water (up to a height of 0.180 m) as shown in Figure 1. The tank is subjected to 30 g peak acceleration at 40 ms [17] in X direction and acceleration due to gravity in vertical downward direction by invoking user defined functions. The material properties for air and water are given below.

1. Air: Density = 1.225 kg/ m³; Dynamic viscosity = 1.784 × 10^-5 kg/ms.

2. Water: Density = 1000 kg/m³; Dynamic viscosity = 0.001 kg/ms.

The air and water are treated as primary and secondary phases respectively. The phase interaction between these two fluids is considered and constant surface tension between these two liquids is taken as 0.072 N/m and this tank is maintained at atmospheric pressure. The total tank is treated as rigid and is made of aluminum solid material.

A typical aircraft drop tank

From the state of art of the grid convergence, the medium grid has been chosen for all computations of different cases. The four cases namely: drop tank without baffle, drop tank with one baffle, drop tank with two baffles, and drop tank with two baffles; 1800 rotation of second baffle. In all the cases the drop is filled with 50% of kerosene by volume (up to a height of 0.32 m) as shown in Figure 3. This drop tank is excited to 7 g peak acceleration in X direction and subjected to acceleration due to gravity in vertical downward direction (-ve Y direction) by source input. The material properties for air and kerosene are as follows.

1. Air: Density = 1.225 kg/ m³; Dynamic viscosity = 1.784 × 10^-5 kg/ms.

2. Kerosene; Density =780 kg/m³; Dynamic viscosity = 0.0024 kg/ms.

The air and kerosene are treated as primary and secondary phases respectively. The surface tension between air and kerosene is taken as 0.025 N/m and the tank is pressurized.

The first section of this chapter gives the detailed description about validation of rigid rectangular tank without baffle for 30 g peak horizontal acceleration for available experimental results. The second section includes application of sloshing phenomenon to a typical aircraft drop tank. This application part has been explained in four cases; without baffle, with one baffle, with two baffles and in two baffles’ case 1800 rotation is being applied to second baffle, and the effect of sloshing on out walls and baffles of aircraft drop tank has been presented for peak 7 g acceleration input. The results obtained from the simulation are satisfactory for both validation and application.

Validation of three-dimensional rectangular tank

Kinematic profiles of water: The contours of water phase at each time instants have been captured and visualized which are shown in Figures 4 - 8. The right side of images are taken by slicing the tank the at the middle section and the lower value (zero) represents empty space, higher value(one) shows the cells which are filled with water and between zero and one shows the interface and/or free surface zone (Figures 4-8).

Figure 4: Interface at time 0 ms.

Figure 5: Interface at time 10 ms.

Figure 6: Interface at time 40 ms.

Figure 7: Interface at time 60 ms.

Figure 8: Interface at time 80 ms.

Pressure variation on tank wall: The hydrostatic pressure at bottom of the tank is initially high. As the solution progresses, the pressure further increases and reaches top, and suddenly falls off as shown in Figure 9. This instantaneous rise in the pressure value is because of acceleration input. The effect of this acceleration on tank wall has been observed. This pressure is measured at a point where the pressure sensor is located as mentioned in [12]. It is evident from the obtained numerical simulation results and experimental values that both results were showing excellent agreement. This gives an insight of sloshing phenomenon when the tank is being accelerated. The 3.30243% error is estimated which is well below the maximum limits.

Figure 9: Pressure vs. time at pressure sensor.

The hydrostatic pressure variation at each time step is shown in the Figures 10-13. These plots are taken from the front view of the tank. The small increment in pressure at the beginning of the solution is observed and when the tank is accelerated at 40 ms, there is rapid rise in the pressure is visualized.

Figure 10: Hydrostatic pressure at 10 ms and 20 ms.

Figure 11: Hydrostatic pressure at 30 ms and 40 ms.

Figure 12: Hydrostatic pressure at 50 ms and 60 ms.

Figure 13: Hydrostatic pressure at 70 ms and 80 ms.

Application of sloshing phoenomenon to a typical drop tank

The sloshing phenomenon is applied to a typical aircraft drop tank. Since fighter aircraft run on white kerosene fuel which is also known as aircraft turbine fuel (ATF), the results obtained using kerosene fuel is depicted in this analysis. The F-16 fighter aircraft can go up to 7.33 g with 80% fuel by volume [16]. The slosh effects have been observed in the form of pressure variation at aft section of drop tank because most of the fuel moves towards rear end section. When the aircraft accelerates this rear section part experiences higher pressure variations. This typical aircraft drop tank is simulated with and without baffle plates. The similar procedure employed in the validation case to simulate sloshing, is being applied for all the afore mentioned cases of drop tank. From the transient simulation the pressure variation on aft section and behavior of kerosene fluid before and after the application of 7 g acceleration input have been observed.

Kinematic profiles of kerosene: From the different cases of drop tank, it is noted that most of the fuel had moved towards the aft section thus putting more pressure in that region. To avoid this effect, a baffle plate had been introduced into the second case, which showed further decrease in the volume of kerosene impacted on the aft section. Furthermore, two baffles and two baffles; 1800 rotation applied to second plate cases had also been observed for visualizing the effect of holes. At different instances of time for different cases, kinematic profiles have been shown in Figures 14-17.

Figure 14: Interface at 300 ms (No baffle case).

Figure 15: Interface at 300 ms (One baffle case).

Figure 16: Interface at 400 ms (Two baffles case).

Figure 17: Interface at 400 ms (Two baffles case; 1800 rotation of 2^nd baffle plate case).

Pressure variation on tank wall: From the pressure vs. time graph in Figure 18, the maximum pressure observed for ‘no baffle’ case is 158.752 kPa, for ‘one baffle’ case is 142.851 kPa, and ‘two baffles’ case is 139.830 kPa. This shows pressure on the rear section is reduced or sloshing loads acting on the walls are decreased with the use of baffle plates. Since each baffle plates are comprise of three holes, in the 4^th case, the 2^nd baffle is rotated to 1800. Pressure variation in rear section is measured. It is observed that maximum pressure is 139.843 kPa which is higher than two baffle case pressure. This is because on 2^nd baffle of ‘two baffles’ case there is only one hole immersed in the kerosene, when 1800 rotation is applied to the 2^nd baffle plate, top two holes will get immersed in kerosene which allow more amount of kerosene to pass through when the tank is accelerated. Thus, the pressure on the rear cone section of drop tank increases. This Figure 18 also gives a proposal on design and development and placement of baffle plates with holes.

Figure 18: Comparison of pressure variation for different cases.

Apart from the rear section of drop tank, the baffle plates which are immersed in the fluid also experience the high pressure due to this accelerating effect of fluid. From the design point of view, it is necessary to establish proper connection between baffle plates and outer wall of the tank. The pressure contour plots for different cases are shown in Figures 19-22.

Figure 19: Pressure variation at 150 ms (No baffle case).

Figure 20: Pressure variation at 50 ms (One baffle case).

Figure 21: Pressure variation at 50 ms (Two baffle case).

Figure 22: Pressure variation at 100 ms (Two baffles; 1800 rotation of 2^nd baffle plate case).

In this research, validation of water sloshing in 3D rigid rectangular tank and an application of sloshing using kerosene to a typical aircraft drop tank or external fuel storage tank has been carried out with the help of explicit transient simulation computational fluid dynamics approach. The rectangular tank is filled with 60% of water and is subjected to 30 g peak acceleration at 40ms. The pressure variation results obtained from simulation are compared with experimental results. Numerical results are showing good agreement experimental data. It is noticed that the maximum pressure is achieved after the application of acceleration input. From the kinematic profiles, the free surfaces of water and kerosene have been clearly observed and from the pressure contours, increments in the static pressure at different time intervals have been visualized.

An optimized design of a typical aircraft drop tank has been modeled by taking drag effects into consideration. To this drop tank, sloshing phenomenon has applied and investigated for with and without baffles. It is evident from the explicit transient simulation method conducted at different time interval that pressure at the rear cone section increases significantly without baffle plates and reduces drastically with the use of baffle plates which acts as damper. The pressure variation for 1800 rotation of one baffle plate (fourth case) actually increased the pressure on rear section side, this is because of large amount of fluid is moving rearwards due to the presence of two holes which are immersed under kerosene. This variation has been visualized from volume fractions. Drop tank with one baffle reduces the peak pressure by 11.25% as compared with no baffle case, drop tank with two baffles reduces the peak pressure by 2% as compared with one baffle case, and two baffle of one baffle reversed condition the peak pressure is reduced by 2.1%. Hence drop tank with one baffle with three holes can be implemented for the design of drop tank.