Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
ISSN: 2157-7544
Research Article - (2017) Volume 8, Issue 3
Keywords: Process simulation; Anhydrous ethanol; Azeotrope; Propylene glycol
Anhydrous ethanol is of great importance in the industry, mainly in the fuel industry. According to the ANP (National Oil Agency) 20- 25% of ethanol is permitted to be added to gasoline in order to increase its octane, improve the performance and reduce the pollution rates, as it decreases the emitted CO2, reducing the emission of greenhouse gases and the energy dependence of fossil fuels. However, for the use of anhydrous alcohol with gasoline, it must be practically free of water (anhydrous), with a minimum of 99.6% alcohol content. According Gomis et al. [1], the water present in ethanol, from its production, causes the formation of two phases when mixed with gasoline in a certain proportion, resulting in engine problems.
The separation of the components of a mixture is of paramount importance in the chemical industry, distillation being the most used separation method, based on the difference in volatility of the components of a liquid mixture [2]. However, some mixtures have characteristics that prevent the total separation of their components, which makes it impossible to use the conventional distillation method.
When a boiling liquid produces a vapor of the same composition and, consequently, the liquid when it evaporates does not alter this composition and occurs the formation of azeotrope, in which the boiling point remains constant, the composition of the vapor phase becomes equal to that of the liquid phase, not allowing its components to be separated by the simple distillation process [3]. The ethanol-water system, for example, forms an azeotrope in compositions close to 0.88, on a molar basis.
It is necessary to use other methods for the dehydration of ethanol, with these systems, such as azeotropic or extractive distillation, consisting of the addition of a third substance in the distillation column, capable of altering the behavior of the liquid-vapor equilibrium in the system and obtaining total separation of its components. What differs from the azeotropic distillation to the extractive distillation is the volatility of the solvent added to the distillation column, where in azeotropic distillation there is the formation of a new azeotrope in the system, which does not occur in the extractive process, making its use more favorable.
The choice of the dehydrating agent should be made in a way that minimizes production costs, has low vapor pressure, has a greater affinity with water so as to entrain as little alcohol and as much water as possible and provide the desired separation using the minimum amount of solvent. Lee [4] reported that the addition of glycols as solvents breaks the ethanol-water azeotrope and changes the liquid-vapor equilibrium curve positively for ethanol dehydration. Ethylene glycol is the most commonly used solvent for the dehydration of ethanol by the extractive distillation method, however it is a slightly toxic compound. For this reason, the search for new solvents that are not harmful to health and the environment has increased.
An important step in the process is the prior characterization of the mixture to be separated. ProSimPlus software is engineering software that performs mass and energy balances for a wide range of industrial processing plants. ProSimPlus solutions are used in the design and operation of existing plants to optimize performance, solve unit problems or maximize the efficiency of industrial plants by providing more than 70 unit operations [5].
On this, the present work aims to study and establish the operational conditions for the extractive distillation of ethanol using propylene glycol as the solvent, through ProSimPlus software. The choice of propylene glycol was performed because it met the requirements of a good solvent and due to the absence of information from it for the breakdown of the ethanol-water azeotrope.
Process simulation
The thermodynamic model of ethanol - water - propylene glycol system was made by ProSimPlus software. Raoult's law modified with γ-Φ approach was used to represent the liquid-vapor equilibrium of the system. The activity coefficient (γ) was used in order to consider the non-ideal liquid phase. The vapor phase was considered ideal due to the process occurring at atmospheric pressure [6], then, Φ=1. Thus, the equation 1 can be written. The NRTL thermodynamic model was used to calculate the activity coefficient, since it corresponds to the results obtained by Meirelles et al. [7].
(1)
The thermodynamic model was validated by calculating the liquidvapor equilibrium in the ProsimPlus simulator. Figures 1 and 2 show the liquid-vapor equilibrium diagrams generated by the ProsimPlus simulator for the ethanol-propylene glycol and water-propylene glycol systems, proving that there is no formation of azeotropes between them, making possible the study of propylene glycol as extractive agent of the ethanol-water system.
Figure 3 shows the liquid-vapor equilibrium curve (101.3 kPa) for the ethanol-water system, generated by the simulator, using the NRTL model.
A pseudo-binary diagram was constructed on a solvent-free basis with the liquid-vapor equilibrium data of the ethanol-water-propylene glycol ternary system. According to NEVES [8], the presence of the solvent in the vapor phase indicates that it is off the mass transfer process. This means solvent do not transfer itself, influencing the process only by its effect on the phase equilibrium. Then, the ternary system can be reduced to the ethanol-water binary system, according to equations 2 and 3:
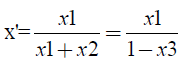 (2)
(2)
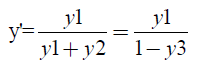 (3)
(3)
x' and y' being the solvent free basis compositions, x1, x2 and x3 the fractions in the liquid phase of ethanol, water and propylene glycol, respectively, and e y1, y2 e y3 the fractions in the vapor phase of ethanol, water and propylene glycol.
Based on the work of Furter, liquid separating agents are generally present between 50 and 90% by weight of the liquid phase. The S/F (propylene glycol/feed) ratio was varied from 0.5; 0.7 and 0.9 by weight for the simulation of the ethanol-water-propylene glycol extraction process.
The “short-cut” distillation column was considered for the process simulation, which uses the project calculation method of Fenske, Underwood and Gilliland. This method aims to obtain an initial estimate of the number of equilibrium stages (N), feeding location (NF) and operating limit conditions: minimum reflux ratio (Rmin) and minimum number of stages (Nmin) (PROSIMPLUS, 2017). Figure 4 shows an illustrative schematic of the simulated process presented by the simulator.
To calculation of the minimum number of theoretical stages, the FUG method uses the Fenske equation for the distillation of multicomponent systems, expressed in equation 4.
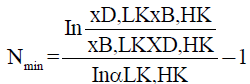 (4)
(4)
being LK the light component (more volatile compound of the system) and HK the heavy component, xB and xD the compositions of the liquid phase of the residue and distillate, respectively. The value of α is given by equation 5.
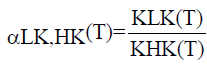 (5)
(5)
The number of ideal stages is determined by the Gilliland correlation, indicated in equation 6.
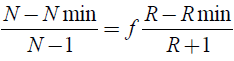 (6)
(6)
The analysis of the minimum reflux ratio is given by the Underwood equation. It is necessary to find the value of A that satisfies equation 7.
Once the value of A is obtained, the minimum reflux ratio, expressed in equation 8, can be calculated.
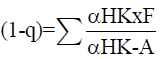 (7)
(7)
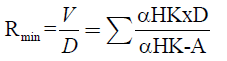 (8)
(8)
Figure 5 shows the pseudo-binary diagram for the ethanol-waterpropylene glycol system. It is possible to observe the influence of the propylene glycol solvent on the liquid-vapor equilibrium, altering the volatility of the system and allowing the breaking of the azeotrope formed in the ethanol-water system, providing a greater dehydration of the ethanol. Thus, the use of propylene glycol in extractive distillation becomes favorable for the production of anhydrous ethanol.
The operational criteria considered efficient were based on the composition of the distillate in the extraction column, which should be 99.6% volume of ethanol. From the results obtained, the fraction of the distillate can be converted in % volume, where it reaches approximately 99.9% ethanol by volume. Table 1 presents the simulation data for the different S/F ratios.
| S/F=0.5 | ||
|---|---|---|
| Components | Mass fraction (distillate) | Molar fraction (distillate) |
| Ethanol | 0.998 | 0.994 |
| Water | 0.002 | 0.006 |
| Propylene Glycol | 0 | 0 |
| S/F=0.7 | ||
| Components | Mass fraction (distillate) | Molar fraction (distillate) |
| Ethanol | 0.998 | 0.994 |
| Water | 0.002 | 0.006 |
| Propylene Glycol | 0 | 0 |
| S/F=0.9 | ||
| Components | Mass fraction (distillate) | Molar fraction (distillate) |
| Ethanol | 0.998 | 0.994 |
| Water | 0.002 | 0.006 |
| Propylene Glycol | 0 | 0 |
Table 1: Results of the simulation process of distillation of the ethanol-water-propylene glycol system.
Tables 2-4 show the effect of each S/F ratio, the minimum reflux ratio, the number of theoretical stages and the energy consumption on the molar composition of the distillate in the extraction column. The best operating condition is given by the simulator, with R/Rmin equal to 1.3. It is possible to observe that, as the S/F ratio increases, there is an increase in energy expenditure, which makes it more favorable to use S/F equal to 0.5, since for the three reasons there was efficiency in the fraction obtained in the distillate of the extraction column.
| R/Rmin | Reflux Ratio | Number of theoretical stages | Condenser Duty (Kcal/h) | Reboiler Duty (Kcal/h) |
|---|---|---|---|---|
| 1.05 | 2.021 | 47 | 242243 | 309583 |
| 1.1 | 2.117 | 42 | 251095 | 317336 |
| 1.2 | 2.310 | 36 | 266599 | 332840 |
| 1.3 | 2.502 | 32 | 282104 | 348345 |
| 1.4 | 2.695 | 30 | 297609 | 363849 |
| 1.5 | 2.887 | 29 | 313113 | 379354 |
| 1.7 | 3.272 | 26 | 344122 | 410363 |
| 2.0 | 3.850 | 24 | 390636 | 456877 |
| 3.0 | 5.775 | 21 | 545682 | 611922 |
Table 2: Operating conditions for S/F=0.5.
| R/Rmin | Reflux Ratio | Number of theoretical stages | Condenser Duty (Kcal/h) | Reboiler Duty (Kcal/h) |
|---|---|---|---|---|
| 1.05 | 2.830 | 60 | 308459 | 446052 |
| 1.1 | 2.964 | 53 | 319312 | 456905 |
| 1.2 | 3.234 | 45 | 341019 | 478612 |
| 1.3 | 3.503 | 41 | 362725 | 500318 |
| 1.4 | 3.773 | 38 | 384431 | 522024 |
| 1.5 | 4.042 | 36 | 406137 | 543730 |
| 1.7 | 4.581 | 33 | 449549 | 587142 |
| 2.0 | 5.390 | 31 | 514668 | 652261 |
| 3.0 | 8.085 | 27 | 731729 | 869322 |
Table 3: Operating conditions for S/F=0.7.
| R/Rmin | Reflux Ratio | Number of theoretical stages | Condenser Duty (Kcal/h) | Reboiler Duty (Kcal/h) |
|---|---|---|---|---|
| 1.05 | 3.808 | 82 | 387268 | 943925 |
| 1.1 | 3.989 | 72 | 401874 | 958531 |
| 1.2 | 4.352 | 61 | 431085 | 987743 |
| 1.3 | 4.715 | 55 | 460297 | 1.02E+06 |
| 1.4 | 5.077 | 52 | 489509 | 1.05E+10 |
| 1.5 | 5.440 | 49 | 518721 | 1.08E+10 |
| 1.7 | 6.166 | 45 | 577144 | 1.13E+10 |
| 2.0 | 7.254 | 42 | 664779 | 1.22E+10 |
| 3.0 | 10.88 | 37 | 956897 | 1.51E+10 |
Table 4: Operating conditions for S/F=0.9.
Due to lack of data in the library using propylene glycol as solvent breaking the azeotrope in the system of ethanol-water, Table 5 presents obtained results from this research just as presents results obtained by Silva et al. [9], this last one analyze azeotrope breaking in the system of ethanol-water using glycerol as third component to extractive distillation with distinct ratios of solvent/load. The ethanol molar fraction at vapor phase is showed like: y ethanol. Silva et al. reported that the results obtained showed that the azeotrope between ethanol and water can be broken by glycerol using the solvent/ feed ratios used in its work. The molar fraction of ethanol in the vapor phase varied in the different S / F ratios, which did not occur in the results obtained in this work. It is possible to observe that, like glycerol, propylene glycol is also effective, positively influencing the liquid-vapor equilibrium curve of the ethanol-water system, making it possible eliminate the azeotrope.
| Results obtained in this work | Results obtained by Silva et al. | |
|---|---|---|
| S/F | y ethanol | y ethanol |
| 0.5 | 0.994 | 0.9945 |
| 0.7 | 0.994 | 0.926 |
| 0.9 | 0.994 | 0.9986 |
Table 5: Comparative data of the molar fraction of ethanol in the vapor phase.
The simulation study made it possible to establish previous operational conditions for an extractive distillation process to eliminate the ethanol-water azeotrope with propylene glycol as solvent. The use of software to characterize the mixture to be separated is of paramount importance in the industry, allowing predicting and improving the process.
The use of propylene glycol as the third component of extractive distillation is technically possible, breaking the azeotrope formed in the ethanol-water mixture and allowing the greater dehydration of the ethanol.
The solvent (propylene glycol) / feed (S/F) ratio did not interfere in the results, obtaining the same fraction of ethanol in the three ratios, being more viable the use of S/F=0.5, due to lower solvent expense and for achieving the composition of the distillate with lower energy consumption.