Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
ISSN: 2157-7544
Research Article - (2015) Volume 6, Issue 2
TCadmium picrate (CdPic2) in water was extracted at 25°C by 18-crown-6 ether (18C6) into o-dichlorobenzene (oDCBz), bromobenzene (BBz), dibutylether (DBE), and nitrobenzene (NB). Their extraction constants (Kex and Kex±) were determined, where Kex and Kex± at L=18C6 were defined as (CdLPic2)o/((Cd2+)(L)o(Pic−)2) and (CdLPic+) o(Pic−)o/((Cd2+)(L)o)(Pic−)2), respectively. The subscript “o” denotes an organic phase, such as oDCBz and BBz. The same extraction constants were re-determined for a system with benzene. Also, individual distribution constants (KD,Pic=(Pic−)o/(Pic−)) of picrate ion Pic− into the above o phases were determined with the Kex determination. Properties for the CdPic2 extraction with 18C6 were discussed by using the above constants and those available from the same extraction systems with other diluents. From comparing the experimental log KD,Pic value with the log KD,Pic S one for only the high-polar NB system, an interfacial potential difference (Δφeq) at extraction equilibrium was evaluated, where the symbol, log KD,Pic S, shows the log KD,Pic value standardized at Δφeq=0 V and 25°C. In the course of this study, an extraction constant for an HPic extraction into DBE was determined spectrophotometrically at 25°C.
Keywords: Extraction constants; Individual distribution constant; Interfacial equilibrium potential; Solute-solvent interaction; At water/ nitrobenzene interface; Cadmium picrate; 18-Crown-6 ether
18-Crown-6 ether (18C6) extracts CdBr2, cadmium picrate (CdPic2), or alkaline-earth metal picrates into various diluents [1-3]. In the previous study [1], the authors clarified that the extracted ion-pair complex, Cd(18C6)Br2, very weakly interacts with water molecules and also the diluents ones and they also suggested that another complex Cd(18C6)Pic2 strongly interacts with water molecules. In addition to this, it has been suggested that the latter ion-pair complex has a more polar structure than the former does [1]. However, kinds of the diluents used for the CdPic2 extraction experiments with 18C6 were fewer, compared with kinds of the diluents for the CdBr2 extraction ones.
In the above studies, furthermore, component equilibria which constitute overall extraction equilibria have been considered to be at least 6-10 ones [1,3,4]. For example, the component equilibria are L 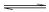 Lo, CdPic+
Lo, CdPic+ 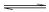 Cd2++Pic-, H++Pic-
Cd2++Pic-, H++Pic- 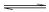 HPic, L+Cd2+
HPic, L+Cd2+ 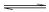 CdL2+, CdL2++Pic-
CdL2+, CdL2++Pic- 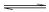 CdLPic+, CdLPic++Pic-
CdLPic+, CdLPic++Pic- 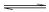 CdLPic2, CdLPic2
CdLPic2, CdLPic2 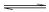 CdLPic2,o , CdLPic2,o
CdLPic2,o , CdLPic2,o 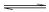 CdLPic+o+Pic−o, Pic
CdLPic+o+Pic−o, Pic 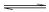 Pic−o, and CdLPic+
Pic−o, and CdLPic+ 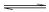 CdLPic+o at L=18C6 [1] where the subscript “o” denotes an organic phase. Unfortunately, except for several studies of the M(II) extraction with dibenzo-18C6 into nitrobenzene (NB) [5,6] the authors have not been able to find out studies based on such precise equilibrium analyses. Also, it is very difficult to criticallyevaluate equilibrium constants determined in the studies of the NB systems, because the corresponding component equilibrium-constants experimentally-obtained from other methods are few.
CdLPic+o at L=18C6 [1] where the subscript “o” denotes an organic phase. Unfortunately, except for several studies of the M(II) extraction with dibenzo-18C6 into nitrobenzene (NB) [5,6] the authors have not been able to find out studies based on such precise equilibrium analyses. Also, it is very difficult to criticallyevaluate equilibrium constants determined in the studies of the NB systems, because the corresponding component equilibrium-constants experimentally-obtained from other methods are few.
In the present paper, by employing o-dichlorobenzene (oDCBz), bromobenzene (BBz), dibutylether (DBE), and NB, we added new data in the CdPic2 extraction by 18C6 and then re-discussed extraction characteristics of 18C6 against CdPic2. Also, extraction constants (Kex and Kex±) for the same extraction into benzene (Bz) were re-determined, because the data of its Bz system abnormally deviated from the plot [1,4] of log Kex,ip versus log KD,L. Here, Kex, Kex±, Kex,ip, and KD,L were defined [MLA2]o/([M2+][L]o[A−]2),[MLA+]o[A−]o/([M2+][L]o[A−]2), [MLA2]o/[ML2+][A−]2, and [L]o/[L] [1,3,4], respectively, with M2+=Cd2+ and A−=Pic. In the above discussion, an interfacial equilibrium-potential difference (Δφeq) at the transfer of Cd2+, CdL2+, CdLPic+, and Pic− from water into the o phase, in particular NB or oDCBz, was introduced, as described previously [3]. Furthermore, an extraction constant of picric acid, HPic, into DBE was determined spectrophotometrically at 25°C, in order to precisely analyze extraction data for the Cd(II) extraction by 18C6 into DBE.
Chemicals
The preparation method of CdPic2·nH2O was essentially the same as that reported before [1]: this n value was determined by a Karl-Fischer titration to be 5.67 ± 0.23 at number (N) of run of 3. This finding was in good agreement with that (n=5.65) obtained from an EDTA titration of Cd(II) in the aqueous solution which contains CdPic2·nH2O. Also, spectrophotometric analysis of Pic (−I) in the aqueous solution at 355.0 nm showed the molar ratio of Cd(II):Pic(−I)=1:2.1 (see below). Water amount of used 18C6 (>98.0%, Wako) was determined by the Karl- Fischer titration to be 0.062 ± 0.029% at N=4. The H(I) amount of an aqueous solution prepared from a commercial HPic (>99.5%, Wako) was determined by an acid-base titration [7]. Other reagents were the same as or similar to those employed previously [1,4].
Extraction procedures
The experimental procedures for the CdPic2 extraction by 18C6 were essentially the same as those described before [1,4] although the experiments were performed with the prepared CdPic2 for the oDCBz (>99.0%, Kanto), DBE (>99.0%, Kanto), NB (>99.5%, Kanto), and Bz (>99.5%, Wako) systems and with mixtures of CdSO4{>99.0%: (3/8) hydrate, Kanto} with HPic for the oDCBz and BBz (>98.0%, Kanto) systems. Here, the mixture was prepared by mixing an aqueous CdSO4 solution with a mixture between Ba(OH)2 (>98.0%: 8 hydrate, Wako) and an excess amount of HPic and then that with the precipitate was filtered. Total amounts of Cd(II) back-extracted from the o phases into aqueous solutions of the 0.1 mol dm-3 HNO3 were determined at the wavelength of 228.8 nm by a Hitachi atomic absorption spectrophotometer (type Z-6100) equipped with a Hitachi hollow cathode lamp (Mitorika Co., under the license of Hitachi Ltd.) of Cd in an air-acetylene flame [1]. Total concentrations employed for the experiments were (0.79-1.7) × 10−2 mol dm-3 for the prepared CdPic2 and 1.1 × 10−5 -0.22 for 18C6; (0.79-1.5) × 10−2 mol dm-3 Cd(II), 0.012- 0.030 Pic(−I), and 0.0017 SO42- for the mixture and (0.051-5.1) × 10-2 for 18C6. Also, the procedures for the HPic extraction into DBE were the same as those reported before [7]. Total amounts of Pic(−I) extracted into DBE were back-extracted into aqueous solutions with 0.1 mol dm-3 NaOH from the DBE phases and then were determined at the wavelength of 355.0 nm spectrophotometrically [7]. Total concentrations of the aqueous HPic solutions employed were in the range of (0.50-3.4) × 10-2 mol dm-3.
Data analysis
Data analysis for the extraction experiments was essentially the same as that described before [1,3,4]. The extraction constant parameter, Kexmix, has been introduced, where Kexmix is defined as ([MLA2]o+[MLA+]o)/([M2+][L]o[A−]2) by assuming that [MLA2]o+[MLA+]o>> [MA+]o+[ML2+]o+[M2+]o [1,3,4]. Its numerators were determined by AAS measurements (see above) and were expressed as “Ab” here. Also, the [M2+], [L]o, and [A−] values were calculated from the following equations by a successive approximation method:
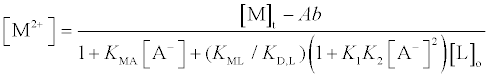 (1)
(1)
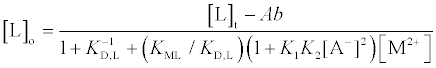 (2)
(2)
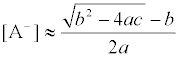 (3)
(3)
With a=2KMLK1K2 [M2+][L]o/KD,L, (3a)
b=1+2KMA[M2+](KHA+Kex,HA)[H+], (3b)
and c=2Ab− [A]t. (3c)
Here, KMA, KML, K1K2, KHA, and Kex,HA in the above equations denote an ion-pair formation constant (mol−1 dm3 unit) for MA+ in water, a complex formation one (mol-1 dm3) for ML2+ in water, overall ionpair formation one (mol−2 dm6) between ML2+ and 2A- in water, an association one(mol-1 dm3) for an acid, HA, in water, and an extraction one (mol−1 dm3) for HA into the o phase, respectively. These values were either available from a reference [8] or evaluated from those [1,9,10] reported previously. Also, [j]t shows the total concentration of species with j=M(II), L, or A(−I). In the computation, the KMA, K1K2, and KHA values were calculated taking account of the ionic strength (I ) of ionic species in water: I=(1/2)(4[M2+]+4[ML2+]+[MLA+]+[MA+]+[A−]) [1,3,4]which was changed into I=[M2+]+[ML2+]+[A−] fundamentally based on the charge balance equation, 2[M2+]+2[ML2+]+[MLA+]+[M A+]=[A−] (see below).
On the determination of fundamental extraction data
Compositions of extracted complexes were determined by plotting log (D/[Pic−]2) against log [18C6]o at o=BBz, oDCBz, DBE, NB, and Bz [1-4,11]. Here, D refers to an experimental distribution ratio of Cd(II) into the o phases and the [Pic−] and [18C6]o values were calculated from Equations (3) and (2), respectively. Regression lines of the plots were lines with slope (a)=0.81 and intercept (b)=3.90 at a correlation coefficient (R)=0.976 and N=11 for the BBz system, a=1.13 and b=4.65 at R=0.972 and N=7 for oDCBz with the mixture, a=0.76 and b=3.39 at R=0.944 and N=18 for oDCBz with the prepared CdPic2, a=1.02 and b=4.61 at R=0.712 and N=23 for DBE, a=0.55 and b=4.80 at R=0.992 and N=15 for NB, and a=0.95 and b=4.28 at R=0.995 and N=15 for Bz. These results indicate that the species composed of M:L:A=1:1:2 are extracted into oDCBz from the mixture, DBE, and Bz, where the ratios of Pic(−I)=A were speculated from the charge balance to Cd(II) (see above) [1,3,4,11]. Also, the intercepts, b of these systems approximately show their log Kex values, when a equals unity [11]. On the other hand, dissociations of the species extracted are suggested for the BBz, NB systems, and oDCBz one with the prepared salt. The difference in a between the two oDCBz systems is caused by that between the experimental log [18C6]oDCBz ranges which were -3.02 to -2.53 for the mixture and -6.73 to -3.09 for the prepared salt. That is, Cd(18C6) Pic2 in the oDCBz phase dissociates in the lower log [18C6]oDCBz range and its ion-pair formation is facilitated in the higher range: the former case causes a < 1, while the latter one does a ≥ 1. Therefore, further data analyses were performed by assuming the extraction of CdLPic2 into the three diluent-systems [3,4,11]. Next, we determined the Kex, KD,A, and Kex± values in terms of the following equations:
logKexmix≈ log {Kex+KD,A/([M2+][L]o[A−])} (4)
and ≈ log {Kex+(Kex±/[M2+][L]o[A−]2)1/2} (4a)
under the electroneutrality condition of [MLA+]o≈ [A−]o[3,4,11]: see Data Analysis. The non-linear regression analyses of plots [1,3,4,11] of log Kexmix versus −log ([M2+][L]o[A−]) {from Equation (4)} and −log {([M2+][L]o)1/2[A−]} {from Equation (4a)} yielded these values. The latter plots were analyzed here by introducing the Kex values, obtained from the former plots, in Equation (4a). As examples, Figures 1 and 2 show the plots for the extraction of the prepared CdPic2 with 18C6 into oDCBz. Lastly, the log K2,org, log KD,MLA2, and log Kex,ip were evaluated from the following thermodynamic cycles: log K2,org = log (Kex/Kex±), log KD,MLA2 = log ([MLA2]o/[MLA2])=log (KexKD,L/KMLK1K2) (see the introduction for the KD,L definition), and log Kex,ip = log (K1K2KD,MLA2)=log (KexKD,L/KML), respectively [3,4]. Table 1 summarizes the thus determined fundamental values.
| Diluenta | log Kex | log Kex± | log KD,A | log K2,org (Iorg)b |
|---|---|---|---|---|
| oDCBz | 4.31 ± 0.07 4.21 ± 0.07e |
-3.03 ± 0.24 -3.26 ± 0.10e | -5.49 ± 0.13 -4.24 ± 0.34e |
7.34 ± 0.25 (2.6 ´ 10-8) 7.46 ± 0.12e (1.6 ´ 10-7) |
| BBze | 4.38 ± 0.08 | -2.67 ± 0.37 | -4.64 ± 0.20 | 7.05 ± 0.37 (7.7 ´ 10-8) |
| DBE | 4.25 ± 0.36 | -3.26 ± 0.31 | -5.07 ± 0.45 | 7.51 ± 0.47 (3.2 ´ 10-8) |
| NB | 6.14 ± 0.06 | 2.25 ± 0.14 | -2.35 ± 0.05 | 1.89 ± 0.15 3.3 ´ 10-5) |
| Diluenta | log KD,MLA2 | log Kex,ip | log K1K2c (I )b | log KD,Ld |
| oDCBz | -3.73, -3.74e | 3.23, 3.13e | 6.96 (0.012), 6.86e (0.025) |
-1.13 |
| BBze | -3.55 | 3.31 | 6.86 (0.026) | -1.12 |
| DBE | -5.51 | 1.53 | 7.04 (0.0058) | -2.77 |
| NB | -1.79 | 5.19 | 6.98 (0.011) | -1.00 |
aAbbreviations of the diluents are as follows: o-dichlorobenzene (oDCBz); bromobenzene (BBz); di butyl ether (DBE); nitrobenzene (NB). bAverage ionic strength values for the o and w phases: mol dm-3 unit. The Iorg values were calculated from Iorg≈ (1/2) ([MLA+]o+[A−]o)=[A−]o=[MLA+]o{>>(1/2)(4[M2+]o+4[ML2+]o+[MA+]o)}. c K1K2 is defined as [CdLPic2]/[CdL2+][Pic−]2 and was calculated from the K1K2 value at I→ 0 reported before [10]. d[14]. eValues obtained from extraction experiments which were performed by using mixtures of Cd2+ with an excess amount of HPic in the presence of SO4 2 in the w phase at pH=2.00-2.90.
Table 1: Fundamental data for the CdPic2 extraction by 18C6 into oDCBz, BBz, DBE, and NB at 25°C.
In Table 1, there were no large differences in log K values between the 18C6 extraction from the prepared salt, CdPic2·5.7H2O, and that from the mixture into oDCBz, except for logKD,Pic. These facts fundamentally show that the BBz system is comparable with the oDCBz, DBE, and NB systems. The difference in log KD,Pic can come from that in IoDCBz, because its value is proportional to the log (Iorg/I ) one in some cases [4]; see below for another detailed explanation.
The log Kex values were in the order DBE ≤ oDCBz ≤ BBz
Plot of log Kex,ip versus log KD,L
Figure 3 shows the re-plot of log Kex,ip versus log KD,L for the various diluent systems [1,4,14] at L=18C6. A point of the NB extraction system seemed to largely deviate from other points. Its regression line in Figure 3 was log Kex,ip=(0.80 ± 0.13)log KD,L+(4.13 ± 0.18) at R=0.894 and N=12 except for the NB system, where the two sets of data were employed for the oDCBz system in the calculation. In CdLX2 crystals at L=18C6 with X=Cl, Br, and I [15,16] and at B18C6 with Cl and Br [17] the two X(−I) bind directly to the central Cd(II) and their positions are perpendicular to the mean plane composed of the donor oxygen atoms in L. These complexes have the hexagonal bi pyramidal geometry. One can easily suppose its structure is kept in o phases with less polarities, except for the NB phase; see the caption in Figure 1 about the o phases. From comparing the log Kex,ip versus log KD,L plot of the Cd(18C6)Pic2 system with that of Cd(18C6)Br2 one (log Kex,ip=1.16log KD,L+5.27 at R=0.993 and N=11 [1,4]), we can immediately see that the plots of the both systems largely differ from each other at the R and slope values. The R value of the Pic− system suggests that the extracted ion-pair complex Cd(18C6)Pic2 has the higher polar structure, compared with Cd(18C6)Br2, and also its slope (=VMLA2/VL) suggests that the complex with Pic(−I) has relatively a compact shape [1,4]. Here, V denotes a molar volume (cm3 mol-1) of the species corresponding to the subscript, MLA2 or L. The VCdLPic2 value was estimated to be 1.7 102 cm3 mol-1from V18C6=214 cm3 mol-1 [14]. This value is in accord with that (=about 200) reported before [1].
Figure 3: Plot of log Kex,ip versus log KD,L at L=18C6. The circles show points of the oDCBz, BBz, DBE, Bz, 1-chlorobutane [1], chloroform [1], 1,2-dichloroethane [1], dichloromethane [1], chlorobenzene [1], toluene [1], and m-xylene [1] extraction systems andthedotted line shows a regression one based on log Kex,ip=(VMLA2/VL)log KD,L+log K1K2+[the constant term] (see text). The triangle shows the point of the NB extraction system.
Since the intercept is expressed as log K1K2+[a term based on interactions between solutes and solvent molecules] [1,14], we can immediately evaluate this latter term from the average log K1K2 value among the extraction systems. This interaction term was calculated to be -2.7, when log K1K2=6.86 was used. This negative sign suggests a strong interaction between water molecules and the ion-pair complex Cd(18C6)Pic2 and/or a weak one between diluent molecules and the complex (see below), compared with the interaction of 18C6 with both the solvent molecules. This suggestion is in agreement with the finding speculated from the R value [1]. The same discussion can be satisfied for the plot of log KD,Cd(18C6)Pic2 versus log KD,18C6 [1].
For the CdPic2 extraction by 18C6 into Bz, we easily obtained from the analysis described in the above section log Kex=4.39 ± 0.04 {or 4.2± 0.1 from Equation (4a)}, log KD,Pic=-5.18 ± 0.11, and log Kex±=-2.97 ± 0.18 {or -2.32 ± 0.20 from Equation (4a) without the fixed Kex}. These values also gave log K2,Bz (=log Kex−log Kex±) =7.4 ± 0.2 at IBz=8.4 × 10−8 mol dm−3 and log KD,CdLPic2=−3.75{= log Kex-log KCdL-log K1K2(average)+log KD,L=4.39 +0.05 − 6.92 (at I=0.019 mol dm−3)-1.27, see above} [1,10,14] at L=18C6. The thus determined log Kex value was used for a recalculation of log Kex,ip: log Kex,ip becomes 3.17 (= log Kex+log KD,L-log KCdL). In this study, the authors correct the log Kex value from 1.98 reported in ref.1 to 4.39 and also do the logarithmic separation factor [4], log (Kex,Pb/Kex,Cd), from 9.73 in ref. 4 to 7.32; the revised log (Kex±,Pb/ Kex±,Cd) value became 7.1. By the re-determination of Kex, the authors will eliminate a problem on the large deviation [1] of the Bz system from the plot of log Kex,ip versus log KD,18C6.
Determination of equilibrium constants for the HPic extraction into DBE
Figure 4 shows a plot of log DA versus pH for the HPic extraction into DBE. A non-linear regression analysis of this plot gave the log Kex,HPic value from its intercept: Kex,HA=[HA]o/[H+][A−]. Here, the relation of
logDA=log Kex,HA-pH-log (1+KHA10-pH) (5) in which the KHA value averaged in the experimental I range (=0.00043-0.022 mol dm−3 at HA=HPic) was introduced, was employed for the analysis [7]. The symbol DA refers to the distribution ratio of species with A−. The line seems to be somewhat higher than the plots in the lower range of pH. This deviation may be due to that of the averaged KHPic. The thus obtained value was log Kex,HPic=1.06 ± 0.01 at 25°C with the regression line at R=0.997. This value was used for the Kex calculation {see Equations (3) and (3b)}. Also, using the average log KHPic value (=0.55 ± 0.03) [8], we evaluated log KD,HPic to be 0.51 ± 0.03. This log KD,HPic value was the smallest of those (=0.89-1.97) [7] reported previously by the authors on the HPic extraction into various diluents.
On the interfacial equilibrium-potential difference at extraction
According to our previous papers [3,18], a difference between log KD,Pic S and log KD,Pic for the NB system shows the presence of an interfacial potential difference,Δφeq, at extraction equilibrium. From the relation [1,3,18]
Δφeq=ΔφA 0′−(2.303RT/F)log KD,A (6)
for the univalent anion A-, we can easily calculate the Δφeq value. Here, the symbol, ΔφA 0′, refers to the formal potential standardized at Δφeq=0 V based on the Ph4As+BPh4− assumption [19] and is expressed as the function log KD,A(= FΔφA 0′/2.303RT)=ΔφA 0′/0.05916 (defined as log KD,AS) at 25°C [1,3,18,20]. Also, F, R, and T show usual meanings. From ΔφPic0′=0.030 V [21] and the log KD,Pic value of the NB extraction system in Table 1, the Δφeq value was calculated to be 0.14 V. At the same time, this value indicates that log KD,Cd, log KD,CdL, and log KD,CdLPic values are expressed as 2(ΔφeqΔφCd0′)/0.05916, 2(Δφeq−ΔφCdL0′)/0.05916,and (Δφeq−ΔφCdLPic 0′)/0.05916 at Δφeq=0.14 V, respectively [3,18]:“+2”of the former two terms refer to the formal charges of Cd2+ and CdL2+ {see Equation (7a)}. The same is essentially true of the other extraction systems, although their ΔφPic 0′ values have not been determined in many cases. For the 1,2-dichloroethane and dichloromethane systems, ΔÏ?Pic 0′ available from references [21,22]. The difference between log KD,Pic values (see Table 1) in the oDCBz extraction system can be explained in terms of those between their charge balance equations, namely the difference between the Δφeq values and is also relevant to the difference between the IoDCBz values (see above). The experimental condition with the extraction of the prepared CdPic2 by L yields the charge balance equation of
2[Cd2+]o+2[CdL2+]o+[CdLPic+]o=[Pic−]o (7)
(or actually [CdLPic+]o≈ [Pic−]o, see above) in the o phase, while the other condition with the extraction of the mixture can yield the equation of 2[Cd2+]o+2[CdL2+]o+[CdLPic+]o+[H+]o+[HL+]o=[Pic−]o (8)
(or similarly [CdLPic+]o+[H+]o+[HL+]o≈ [Pic−]o). Probably, the [H+]o+[HL+]o term in Equation (8) corresponds to an increase in Io for the extraction of the mixture with L (see Table 1).
Applying Equiation (6) to Equation (7) and the term in Equation (8), we can rewrite them as
2[Cd2+]exp{2F(Δφeq−ΔφCd 0′)/RT}+2[CdL2+]exp{2F(Δφeq−φCdL 0′)/ RT}
+[CdLPic+]o=[Pic−]exp{−F(Δφeq − ΔPic 0′)/RT} (7a)
and [H+]exp{F(Δφeq−ΔφH 0′)/RT}+[HL+]exp{F(Δφeq−ΔφHL 0′)/ RT},(8b)
respectively [18,23]. The symbol Δφj 0′ denotes the standard formal potential for the species j {= Cd(II), CdL(II), CdLPic(I), Pic(−I), H(I), and HL(I)}. Defining x=exp(FΔφeq/RT) in Equation (7a) or Equation (8a) that Equation (8b) was added to the left-hand side of Equation (7a), then we can easily obtain the cubic equations, ax3+bx+c=0, solve them for x, and also for Δφeq [18,23]. For example, a=2[Cd2+]exp(- 2FφCd 0′/RT)+ 2[CdL2+]exp(-2FφCdL 0′/RT), b=[CdLPic+]o(see below for the NB system), and c=-[Pic−]exp(FΔφPic 0′/RT) in the case of Equation (7a).
One can easily see that this Δφeq value is common to all processes of Cd2+  Cd2+ o, CdL2+
Cd2+ o, CdL2+  CdL2+o, CdLPic+
CdL2+o, CdLPic+  CdLPic+ o, and Pic−
CdLPic+ o, and Pic− 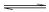 Pic−o or to those of Cd2+
Pic−o or to those of Cd2+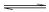 Cd2+ o,CdL2+
Cd2+ o,CdL2+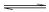 CdL2+o,CdLPic+
CdL2+o,CdLPic+ 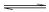 CdLPic+o, H+
CdLPic+o, H+ 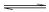 H+ o, HL+
H+ o, HL+ 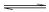 HL+ o, and Pic
HL+ o, and Pic 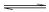 Pic−o[18] at o=oDCBz. Thus, these Δφeq values solved by the above charge-balance equations are equivalent to those determined from log KD,Pic [18] and accordingly both the Δeq values can reflect materials employed in extraction experiments. Therefore, the upper log KD,Pic value (= -5.49) in Table 1 is different from the lower value (=-4.24) and the increase in the lower value from Equation (7) can be caused by Equation (8b). Unfortunately, we were not able to find out the basic Δj 0′ data {j=Cd(II), Pic(−I), or H(I)} in references with respect to the oDCBz system.
Pic−o[18] at o=oDCBz. Thus, these Δφeq values solved by the above charge-balance equations are equivalent to those determined from log KD,Pic [18] and accordingly both the Δeq values can reflect materials employed in extraction experiments. Therefore, the upper log KD,Pic value (= -5.49) in Table 1 is different from the lower value (=-4.24) and the increase in the lower value from Equation (7) can be caused by Equation (8b). Unfortunately, we were not able to find out the basic Δj 0′ data {j=Cd(II), Pic(−I), or H(I)} in references with respect to the oDCBz system.
Estimate of ion-transfer formal potential of CdLPic+ at the water/NB interface
On the basis of the above discussion, the ΔφCdLPic 0′ value at the water/ NB interface was evaluated at L=18C6. The [CdLPic+]NB values were evaluated from the relation [MLA+]o=(Kex mix−Kex)[M2+][L]o[A−]2 (>0) and then the [CdLPic+] ones were calculated from [MLA+]=K1[ML2+] [A−]=(K1KML/KD,L)[M2+][L]o[A−]. Here, K1 was evaluated from the relation log K1{= log K10-log (yII+y−/yI+)}≈ log K10-log yII+ with y−≈yI+. The symbols, K10,yII+, y−, and yI+, denote K1 at I 0, an activity coefficient of ML2+, that of A−, and that of MLA+ in water at 25°C, respectively [10,24]; K1 0=3.4 × 104 mol−1 dm3. From the above calculation, −0.43(± 0.15 at N=8) was obtained as the average log KD,CdLPic value. Hence, using the equation (Δφeq-ΔφCdLPic 0′)/0.05916=log KD,CdLPic and Δφeq=0.14 V (see above), we immediately was able to calculate ΔφCdLPic 0′ to be 0.17 V at 25°C. This value is much larger than that (ΔφPic 0′=0.003 V) [21] of Pic− in the ion transfer at the water/NB interface. This fact suggests the stronger interaction of CdLPic+ than Pic− with water molecules, as described above.
By adding the log Kex,ip values for the three diluent systems except for the NB one, the plot of log Kex,ip versus log KD,L for the present CdPic2-18C6 extraction system was re-analyzed in the number of data comparable with the plot of the CdBr2-18C6 extraction one. Although the extraction data for the Bz system were revised, the result for the interaction between Cd(18C6)2+(Pic-)2 and water molecules, obtained from the former plot, was in agreement with the previously-reported result [1]. Also, the presence of Δφeq in the Cd(II) extraction system was shown from the KD,Pic determination, as well as that in the M(I) extraction ones with L. Moreover, the authors were able to estimate the ion-transfer formal potential of Cd(18C6)Pic+ at the water/NB interface.