Journal of Theoretical & Computational Science
Open Access
ISSN: 2376-130X
ISSN: 2376-130X
Research Article - (2015) Volume 2, Issue 4
Extensive vibrational spectroscopic investigations along with theoretical quantum chemical studies on 2-methoxy-1,3-dioxolane (MDOL) have been consummated. The experimentally observed spectral data (FT-IR and FT-Raman) of the title compound were compared with the spectral data obtained by DFT/B3LYP method. The 1H and 13C nuclear magnetic resonance (NMR) spectra were simulated by using the gauge independent atomic orbital (GIAO) method and the absolute chemical shifts related to TMS were compared with experimental spectra. The theoretical UV-Visible spectrum of the title compound was measured in different solvent and the electronic properties, such as excitation energies, oscillator strength and wavelengths were performed by time-dependent density functional theory (TD-DFT) approach. The kinetic stability of the molecule has been determined from the frontier molecular orbital (FMO) energy gap. Total density of state (TDOS) and partial density of state (PDOS) of the MDOL in terms of Mulliken population analysis Topological parameters at bond critical point have been analyzed in MDOL by Bader’s were calculated and analyzed. Reduced density gradient (RDG) of the MDOL was given to investigate interactions of the molecule. ‘Atoms in molecules’ (AIM) theory in detail. In addition, the temperature dependence thermodynamic properties and magnetic susceptibility of MDOL were calculated with the help of DFT/ B3LYP method using 6-311++G(d,p) basis set.
<Keywords: 2-methoxy-1,3-dioxolane; FMO; DOS; RDG; AIM
Dioxolane and its derivatives are widely used in natural product syntheses as protecting groups for aldehydes, ketones and 1,2-diols. 1,3-Dioxolane derivatives, which have been used in commercial purposes and industrial including important intermediates, pharmaceutical manufacturing, fragnance and polymer industries have been studied extensively [1-3]. Aryl, alkyl, imidazole, triazole, pyrazole, benzimidazole, benzotriazole, oxypurine, pyrimidinyl and naphtyl groups are linked to 1,3-dioxolane ring at different positions like 2, 4 or 5. Depending on the position of the substituents, these compounds exhibit a broad spectrum of biological activities such as antifungal [4], antibacterial [5,6], antineoplastic [7], antiviral [8,9], anesthetic [10,11] and anticonvulstant ones [12]. According to the literature survey, several 1,3-dioxolanes are used co-monomer for manufacture of polyacetals and other polymers, solvent for chemical reactions (including inorganic salts), stabilizer for halogenated organic solvents and as a starting material or reagent for organic synthesis [13]. Among the major biological activities, 1,3-dioxolane is a powerful aprotic solvent for use in formulations, in production processes and good toxicity profile. In recent years, among the computational methods calculating the electronic structure of molecular systems, DFT has been favourite one due to its great accuracy in reproducing the experimental values in molecular geometry, vibrational frequencies, atomic charges, dipole moment, thermodynamic properties, etc. [14-16]. Literature survey reveals that to the best of our knowledge, no experimental and computational spectroscopic study on 2-methoxy- 1,3-dioxolane (MDOL) has been published in the literature yet. This inadequacy is observed in the literature encouraged us to make this theoretical and experimental vibrational spectroscopic study to give a correct assignment of the fundamental bands in the experimental FT-IR and FT-Raman spectra. The isotropic chemical shifts and electronic transitions were analyzed by NMR and UV spectroscopic techniques. The work also encompasses calculation of thermodynamic and magnetic properties, frontier molecular orbital, density of states (DOS), reduced density gradient (RDG), natural bond orbital (NBO) analysis and topological parameters. Related to this phenomenon, with the hope the results of present study may be helpful in the prediction of its mechanism of biological activity.
The compound 2-methoxy-1,3-dioxolane (MDOL) in liquid state is purchased from Sigma Aldrich Chemical Suppliers with the stated purity of 98%. Then the compound is used as such for spectral measurements without further purification. In the present study, the Fourier transform infrared spectrum (FT-IR) of the title compound is recorded in the wavenumber region 4000-400 cm-1 on a NEXUS 670 spectrophotometer equipped with an MCT detector in a KBr pellet technique. The FT-Raman spectrum is recorded in the wavenumber region 3500-100 cm-1 on a NEXUS 670 spectrophotometer equipped with Raman module accessory operating at 1.5 W power with Nd:YAG laser of wavelength 1064 nm is used as an excitation source. The 1H (400 MHz; CDCl3) and 13C (100 MHz; CDCl3) nuclear magnetic resonance (NMR) spectra were recorded on a BRUKER HC400 instrument using CDCl3 solvent. Chemical shifts for protons are reported in parts per million (ppm) scales (δ scale) downfield from tetramethylsilane.
The combination of vibrational spectroscopy along with quantum chemical calculations is effective for understanding the fundamental mode of vibrations of the title compound. The quantum chemical calculations have been performed with GAUSSIAN-09W [17] program, invoking gradient geometry optimization [18]. The density functional theory (DFT) [19] with the three parameter hybrid functional (B3) [20,21] for the exchange part and the Lee-Yang-Parr (LYP) correlation functional [15] have been utilised for the computation of molecular structure optimization, vibrational frequencies, thermodynamic properties and energies of the optimized structure. All the computations have been done by adding‘d’ polarization functions on heavy atoms and ‘p’ polarization functions on hydrogen atoms as well as diffuse functions for both hydrogen and heavy atoms [22-25]. The absolute Raman and IR absorption intensities were calculated in the harmonic approximation at the same level of theory as used for the optimized geometries associated with each normal mode, respectively. The normal coordinate analysis was performed and the potential energy distribution (PED) was calculated along the internal coordinates using localized symmetry.
The vibrational modes were assigned by means of visual inspection using Gauss View 5.0 program [26]. The vibrational mode analysis of MDOL is presented in some detail inorder to better describe the basis for the assignments, from the basic theory of Raman scattering. A comparison is made between the theoretically calculated frequencies and the experimentally measured frequencies. In this investigation it was observed that the calculated frequencies were slightly greater than the fundamental frequencies. To improve the agreement between the predicted and observed frequencies, the computed harmonic frequencies are usually scaled for comparison. In this work, the force field was scaled according to the SQM procedure [27] and the Cartesian representation of the force constants were transferred to a nonredundant set of local symmetry coordinates, chosen in accordance to the recommendations of Pulay et al. [28]. Calculation of the potential energy distribution (PED) and the prediction of IR intensities and Raman activities were done on a PC with the MOLVIB Program (Version V7.0-G77) written by Sundius [29,30].
The prediction of Raman intensities were carried out by the following procedure outlined below. The Raman activities (Si) calculated by GAUSSIAN-09W and adjusted during scaling procedure with MOLVIB were converted to relative Raman intensity (Ii) using the following relation from the basic theory of Raman scattering [31,32].

Where v0 is the laser exciting wavenumber in cm-1 (in this work, we have used the excitation wavenumber v0=9398.5 cm-1, which corresponds to the wavelength of 1064 nm of a Nd:YAG laser), vi is the vibrational wavenumber of the ith normal mode (in cm-1) and Si is the Raman scattering activity of the normal mode vi, f (is a constant equal to 10-12) is a suitably chosen common normalization factor for all the peak intensities. h, k, c and T are Planck constant, Boltzmann constant, speed of light and temperature in Kelvin, respectively.
Molecular geometry
The geometry of a molecule can be characterised by analysing the bond length and bond angle. Bond length and bond angle are the two important parameters which determine the shape and size of a molecule. Bond length is the distance between the nuclei of two bonded atoms whereas bond angle is the angle formed between two adjacent atoms in a molecule. They always range from 100 to 180 degrees. A dihedral angle or torsion angle is the angle between two planes. It defines the conformations around rotatable bonds. The dihedral angle changes only with the distance between the first and fourth atoms; the other inter atomic distances are controlled by the chemical bond lengths and bond angles. Its value ranges from -180° to +180°. The torsion angle is considered to be positive if a clockwise rotation is performed with the molecule and it will be negative when an anticlockwise rotation is performed with the molecule in its plane. The molecular structure and the numbering of the atoms of MDOL are shown in Figure 1. The values of important geometrical parameters like bond lengths, bond angles and dihedral angles of the optimized MDOL molecule are determined by B3LYP level with 6-311++G(d,p) as basis set and found in close agreement with experimental parameters obtained from the X-Ray diffraction studies [33] as shown in Table 1. The observed C2-O1, C2-O3, C4-O3 and C5-O1 bond length values were found to be 1.358, 1.358, 1.428 and 1.428 Å and the calculated bond length values were 1.386, 1.413, 1.438 and 1.435 Å by B3LYP method using 6-311++G(d,p) basis set. Furthermore, O3-C2-O1 and C4-O3-C2 bond angles in the structure were observed at 111.67 and 108.71°, corresponding angle value were calculated at 107.19 and 107.89° by B3LYP with 6-311++G (d,p) basis set, respectively. For visual depiction of optimized geometrical parameters of MDOL under B3LYP/6-311++G(d,p) level, has been shown in Figures 2-4, respectively. From the theoretical results of the title molecule, one could find that the optimized bond lengths and angles are slightly smaller as well as longer than the experimental value, this is due to the fact that the theoretical calculations belongs to isolated molecule in gaseous phase and the experimental results belongs to molecule in liquid state. The internal coordinates and local symmetry coordinates of MDOL were shown in Supplementary document, Tables S1 and S2 respectively.
| Tag | Symbol | NA | NB | NC | Bond length (Å) | Bond angle (°) | Dihedral angle (°) | ||
|---|---|---|---|---|---|---|---|---|---|
| Theorya | Expt.b | Theorya | Expt.b | Theorya | |||||
| 1 | O | ||||||||
| 2 | C | 1 | 1.386 | 1.358 | |||||
| 3 | O | 2 | 1 | 1.413 | 1.358 | 107.188 | 111.67 | ||
| 4 | C | 3 | 2 | 1 | 1.438 | 1.428 | 107.889 | 108.71 | 22.430 |
| 5 | C | 1 | 2 | 3 | 1.435 | 1.428 | 105.716 | -35.481 | |
| 6 | H | 2 | 1 | 5 | 1.095 | 110.071 | -153.414 | ||
| 7 | O | 2 | 1 | 5 | 1.402 | 108.494 | 85.191 | ||
| 8 | C | 7 | 2 | 1 | 1.424 | 113.835 | 175.654 | ||
| 9 | H | 8 | 7 | 2 | 1.094 | 111.338 | 64.260 | ||
| 10 | H | 8 | 7 | 2 | 1.089 | 106.540 | -176.137 | ||
| 11 | H | 8 | 7 | 2 | 1.098 | 111.004 | -57.558 | ||
| 12 | H | 4 | 3 | 2 | 1.093 | 108.102 | -121.099 | ||
| 13 | H | 4 | 3 | 2 | 1.092 | 109.928 | 119.540 | ||
| 14 | H | 5 | 1 | 2 | 1.089 | 107.788 | 153.743 | ||
| 15 | H | 5 | 1 | 2 | 1.093 | 110.061 | -86.440 | ||
For numbering of atom refer Figure 1.
aTheoretical values are calculated by DFT/B3LYP/6-311++G(d,p) method.
bExperimental values are taken from Ref. [33].
Table 1: Geometrical parameters such as bond lengths, bond angles and dihedral angles of 2-methoxy-1,3-dioxolane molecule calculated at DFT/B3LYP/6- 311++G(d,p) method.
Vibrational assignments
Inorder to obtain the spectroscopic signature of the MDOL, the computational calculations are performed for frequency analysis. The title molecule contains 15 atoms and hence it has 39 normal modes (3N-6) of vibrations. The harmonic vibrational frequencies calculated at B3LYP level with 6-311++G(d,p) basis set and observed FT-IR and FT-Raman frequencies for various modes of vibrations have been presented in Table 2. The vibrational assignments are made on the basis of the spectral regions of the respective modes and with the help of Gauss View 5.0 visualisation program. The calculated vibrational frequencies were in good agreement with the experimental results. The observed and theoretical FT-IR and FT-Raman spectra of the title compound are shown in Figures 5 and 6, respectively.
| S No | Observed frequency (cm-1) | Calculated frequency (cm-1) | IR Intensity | RamanIntensity | Assignmentsalong with PED (%) | ||
|---|---|---|---|---|---|---|---|
| FT-IR | FT-Raman | Unscaled | Scaled | ||||
| 1 | 3139 | - | 3169 | 3142 | 20.74 | 8.74 | CH3ips(100) |
| 2 | - | 2960 | 3122 | 2971 | 29.92 | 10.65 | CH2ass(100) |
| 3 | 2946 | - | 3087 | 2972 | 27.80 | 8.52 | CH2ass(100) |
| 4 | - | 2909 | 3064 | 2913 | 31.58 | 6.59 | CH3ss(100) |
| 5 | 2905 | - | 3056 | 2909 | 39.60 | 19.42 | CH(99) |
| 6 | - | 2841 | 3047 | 2847 | 47.02 | 12.17 | CH2 ss(99) |
| 7 | 2839 | - | 3044 | 2846 | 56.24 | 9.46 | CH2 ss(99) |
| 8 | 2813 | - | 2994 | 2821 | 57.90 | 16.12 | CH3ops(96) |
| 9 | - | 1534 | 1588 | 1542 | 0.93 | 2.45 | CH2sciss(87) |
| 10 | - | 1527 | 1534 | 1531 | 5.71 | 2.40 | CH2 sciss(88) |
| 11 | 1521 | - | 1511 | 1526 | 6.89 | 6.35 | CH3ipb(84) |
| 12 | 1494 | 1499 | 1487 | 1498 | 6.39 | 5.86 | CH3sb(86) |
| 13 | 1445 | - | 1473 | 1449 | 5.03 | 0.68 | CH3opb(88) |
| 14 | 1373 | - | 1398 | 1378 | 31.25 | 1.24 | CH2 wag(80) |
| 15 | - | 1362 | 1379 | 1367 | 14.45 | 3.45 | bCH(77), Rbend2(21) |
| 16 | - | 1329 | 1371 | 1331 | 1.09 | 1.67 | CH2wag(81) |
| 17 | 1304 | - | 1321 | 1309 | 7.51 | 3.56 | ωCH(69), tR torsion(23) |
| 18 | - | 1226 | 1246 | 1231 | 4.23 | 4.13 | CH2twist(79) |
| 19 | - | 1211 | 1222 | 1216 | 21.68 | 1.88 | CH2 twist(80) |
| 20 | 1204 | - | 1221 | 1209 | 3.89 | 5.42 | CH3opr(77) |
| 21 | 1139 | - | 1174 | 1142 | 2.85 | 2.07 | CH3ipr(73) |
| 22 | 1124 | - | 1157 | 1127 | 36.85 | 0.23 | Rbend1(71), bCC(23) |
| 23 | 1076 | - | 1143 | 1079 | 202.97 | 1.04 | CO(74), Rbend1(21) |
| 24 | 1037 | - | 1099 | 1041 | 250.33 | 3.30 | CO(76), bCH(19) |
| 25 | 1019 | - | 1041 | 1022 | 69.14 | 0.55 | CO(75), CH(23) |
| 26 | 987 | - | 992 | 993 | 94.42 | 4.56 | CO(88), Rbend(10) |
| 27 | 973 | - | 981 | 979 | 122.71 | 6.62 | CO(77), bCO(21) |
| 28 | - | 947 | 955 | 951 | 46.43 | 8.30 | CC(73), bOCH3(19) |
| 29 | - | 920 | 940 | 927 | 67.55 | 7.62 | CO(81) |
| 30 | 847 | - | 867 | 851 | 6.42 | 2.13 | CH2rock(70) |
| 31 | - | 800 | 811 | 804 | 5.09 | 6.06 | Rbend1(69), CH(17) |
| 32 | 663 | - | 696 | 667 | 5.22 | 2.73 | CH2rock(67) |
| 33 | 616 | - | 543 | 621 | 5.16 | 3.44 | bCO(60), CC(21) |
| 34 | 561 | - | 508 | 566 | 2.13 | 7.09 | Rbend2(59), Rbend1(27) |
| 35 | 498 | - | 302 | 501 | 1.71 | 5.45 | bOCH3(69), Rbend2(19) |
| 36 | - | - | 191 | 201 | 6.60 | 2.14 | CH3 twist(58) |
| 37 | - | - | 157 | 168 | 6.67 | 3.42 | tR torsion 1(56), ωCH(21) |
| 38 | - | - | 110 | 116 | 4.00 | 9.70 | ωOCH3(57) |
| 39 | - | - | 46 | 53 | 3.88 | 100 | tR torsion 2(57) |
For numbering of atom refer Figure 1.
aTheoretical values are calculated by DFT/B3LYP/6-311++G(d,p) method.
bExperimental values are taken from Ref. [33].
Table 2: The observed (FTIR and FT-Raman) and calculated (Unscaled and Scaled) frequencies (cm-1) using B3LYP /6-311++G (d, p) along with their probable assignments and potential energy distribution (PED) of 2-methoxy-1,3-dioxolane.
C-O vibrations: The C-O stretching vibration [34-36] is expected in the region 1300-1000 cm-1 , and is very intense in the infrared and only moderately active in Raman. However, in the present study the C-O stretching vibration is observed in the region between 1076 - 920 cm-1 in FT-IR and FT-Raman spectra, for MDOL. The C-O in-plane and the out-of-plane bending vibrations are expected in the regions 725 ± 70 cm-1 and 540 ± 80 cm-1, respectively [37,38]. In the title compound, the in-plane bending vibration is identified at 616 cm-1 in FT-IR spectrum.
C-H vibrations: C-H stretching vibrations [39,40] of heterocyclic structure were observed within the region 3100-3000 cm-1. In MDOL, the C-H stretching vibration is found at 2905 cm-1 in FT-IR spectrum. The C-H in-plane and out-of-plane bending vibrations [41] were generally lie in the region 1300 - 1000 cm-1 and 1000 - 675 cm-1, respectively. In accordance with literature, in the present study, the bands observed at 1362 cm-1 in FT-Raman spectrum and 1304 cm-1 in FT-IR spectrum were assigned to C-H in-plane and out-of-plane bending vibrations, respectively.
CH2 vibrations: For the assignments of CH2 group frequencies, basically six fundamentals can be associated to each CH2 group namely, CH2 ss - symmetric stretch; CH2 ass - asymmetric stretch; CH2 sciss - scissoring and CH2 rock - rocking which belong to in-plane vibrations and two out-of-plane vibrations, viz., CH2 wag - wagging and CH2 twist - twisting modes, which are expected to be depolarized [42]. The asymmetric CH2 stretching vibrations are generally observed above 3000 cm-1, while the symmetric stretch [43] will appear in the region 3000 and 2900 cm-1. In this study, the asymmetric and symmetric stretching vibrations are observed at 2960, 2946 and 2841, 2839 cm-1 in FT-Raman and FT-IR spectra, respectively. The CH2 scissoring vibrations [44] appear normally in the region 1490 - 1435 cm-1. For MDOL, The CH2 scissoring modes are assigned at 1534 and 1527 cm-1 in FT-Raman spectrum, respectively. Similarly, the CH2 rocking, wagging and twisting vibrations are also established within the characteristic region and are attributed in Table 2.
CH3 vibrations: For the assignment of CH3 group frequencies, nine fundamental vibrations can be associated with each CH3 groups. Three stretching, three bending, two rocking modes and single torsional mode describe the motion of the methyl group [45]. The C-H methyl group stretching vibrations [46,47] are generally observed in the range 3000 - 2800 cm-1. Hence in the present investigation, the FT-Raman band observed at 2909 cm-1 has been assigned to CH3 symmetric stretching vibration. The FT-IR bands found at 3139 and 2813 cm-1 have been assigned to CH3 in-plane and out-of-plane stretching vibrations for MDOL. The methyl deformation modes mainly coupled with the inplane bending vibrations and are also well established. The in-plane methyl deformation mode of MDOL is found at 1521 cm-1 in FT-IR spectrum. The bands at 1445 and 1204 cm-1 in FT-IR is attributed to CH3 out-of-plane deformation modes of MDOL. The methyl rocking modes of vibration [48-50] usually appears within the region 1070 - 1010 cm-1. With reference to literature data, the observed band at 1139 cm-1 is assigned to in-plane CH3 rocking vibration for MDOL. The twisting vibrations are not observed in the FT-IR and FT-Raman spectrum because these appear at very low frequency.
NMR spectral studies
NMR spectroscopy is currently used for structure and functional determination of biological macromolecules. Recent advances in experimental and computational techniques have made it possible to exploit NMR chemical shifts to obtain structures of proteins and macromolecules [51]. The optimized molecular structure of the title compound was used to simulate 1H and 13C NMR spectra of the molecule at DFT/B3LYP/6-311++G(d,p) level using the Gauge- Including Atomic Orbital(GIAO) method in which an exponential term containing the vector potential is including with each atomic orbital. The calculated 1H and 13C NMR chemical shifts of the title molecule in gas phase, taking trimethylsilane (TMS) as a reference, is given in Table 3 along with the experimentally observed values. The atom positions are listed according to Figure 1. The recorded 1H and 13C NMR spectra in CDCl3 solution are as shown in Figures 7 and 8, respectively. Normally, the range of 13C NMR chemical shifts is greater than 100 ppm [52] and the accuracy ensure that the reliable interpretation of spectroscopic parameters. In the case of MDOL, the calculated chemical shift of C2, C4, C5 and C8 are 134.91, 64.73, 63.89 and 51.68 ppm, respectively as shown in Table 3. The shift is less in C8 (expt. 51.45 ppm) than rest of others. This is mainly due to the breaking of paramagnetic shield of proton by the substitutions of oxygen and methyl group. The C2 in the ring has more shifted than other due to the delocalization of σ and π electrons.
| Atoms | Isotropic chemical shifts (ppm) | |
|---|---|---|
| B3LYP | Experimental | |
| 13C | ||
| C2 | 134.91 | 115.96 |
| C4 | 64.73 | 64.09 |
| C5 | 63.89 | 64.09 |
| C8 | 51.68 | 51.45 |
| 1H | ||
| H6 | 5.06 | 5.74 |
| H9 | 3.05 | 3.32 |
| H10 | 2.94 | 3.32 |
| H11 | 2.48 | 3.32 |
| H12 | 2.85 | 3.96 |
| H13 | 3.23 | 4.08 |
| H14 | 3.11 | 4.08 |
| H15 | 3.02 | 3.96 |
Table 3: Theoretical and experimental 1H and 13C NMR Isotropic chemical shifts (with respect to TMS, all values in ppm) of 2-methoxy-1,3-dioxolane.
Generally, the proton chemical shift of organic molecules varies greatly with the electronic environment of the proton. Hydrogen attached or nearby electron-withdrawing atom or group can decrease the shielding and move the resonance of attached proton towards to a higher frequency, whereas electron-donating atom or group increases the shielding and moves the resonance towards to a lower frequency [53]. There are eight hydrogen atoms (ring and CH3 group) in the title molecule. The chemical shifts of aromatic protons of organic molecules are usually observed in the region 6.15 - 6.17 ppm [54]. The calculated and observed proton chemical shifts are attributed in Table 3. The chemical shifts of aromatic protons of organic molecules are higher than the other protons. Therefore, the electronic charge density around of these atoms can be affected the influence of rapid proton exchange, hydrogen bond, solvent effect, etc. in the molecular system.
UV-Vis spectral analysis
The analysis of the wave function indicates that the electron absorption corresponds to the transition from the ground to the first excited state and is mainly described by one-electron excitation from the highest occupied molecular orbital (HOMO) to lowest unoccupied molecular orbital(LUMO). In order to understand electronic transitions of compound, time dependent DFT(TD-DFT) calculations on electronic absorption spectrum were performed for MDOL by B3LYP/6- 311++G(d,p). The calculated absorption wavelengths (λ), oscillator strengths (f) and excitation energies (E) of molecule in gas phase as well as water, ethanol and methanol solvent medium were given in Table 4. The electronic transition predicted by TD-DFT/B3LYP/6- 311++G(d,p) method as shown in Figure 9. According to Frank- Condon principle, the maximum absorption peaks (λmax) correspond in a UV-Vis spectrum to vertical excitation. Life spans of first excited state for solvents were calculated applying the definition τ=1.499/f(E2) in which E (in cm-1) is the energy gap between ground state and a given excited state; f is the oscillator strength of excited state [55]. It is seen from Table 4, calculations performed at water, ethanol and methanol were close to each other when compared with gas phase and also the absorption maxima values of gas phase are larger than that of the organic solvents.
| Solvent | Excitation | Wave length (nm) | Oscillator strength (f) | Energy(eV) | Life span (τ) |
|---|---|---|---|---|---|
| Gas | HOMO→LUMO | 189.62 | 0.0104 | 6.5386 | 0.05 |
| HOMO-1→LUMO | 181.26 | 0.0053 | 6.8401 | 0.09 | |
| HOMO-1→LUMO | 176.82 | 0.0043 | 7.0118 | 0.10 | |
| Water | HOMO→LUMO | 178.93 | 0.0075 | 6.9294 | 0.06 |
| HOMO-1→LUMO | 172.00 | 0.0019 | 7.2085 | 0.23 | |
| HOMO-1→LUMO | 169.05 | 0.0024 | 7.3341 | 0.17 | |
| Ethanol | HOMO→LUMO | 179.31 | 0.0081 | 6.9145 | 0.05 |
| HOMO-1→LUMO | 172.38 | 0.0020 | 7.1923 | 0.22 | |
| HOMO-1→LUMO | 169.31 | 0.0022 | 7.3229 | 0.19 | |
| Methanol | HOMO→LUMO | 179.17 | 0.0078 | 6.9201 | 0.06 |
| HOMO-1→LUMO | 172.24 | 0.0019 | 7.1985 | 0.23 | |
| HOMO-1→LUMO | 169.21 | 0.0023 | 7.3271 | 0.18 |
Table 4: Calculated electronic absorption spectral data of 2-methoxy-1,3-dioxolane
Thermodynamic properties
The calculation of thermodynamic properties of MDOL includes total internal energy (E or U), entropy (S) and heat capacity at constant volume (Cv). These thermodynamic attributes has been calculated by DFT/B3LYP/6-311++G(d,p) method. The E, S, and Cv are contributed from the translational, rotational and vibrational motions along with the partition function of corresponding components [56]. The entropy (S) can be calculated from the partition function of any motion [57] by the given relation,

The E is derived from the given partition function,

But the Cv can be derived from E which as follows,

The participation of S, E, and Cv with respect to translational, rotational and vibrational molecular motion at different temperatures ranging from 100 K to 1000 K is tabulated and shown in Table 5. The translational partition function (qt) is implemented to calculate entropy contributed from translational motion (St). The mathematical relationship for St can be given by,
| Temperature (K) | Translational motion | Rotational motion | Vibrational motion | ||||||
|---|---|---|---|---|---|---|---|---|---|
| St | Et | Ct | Sr | Er | Cr | Sv | Ev | Cv | |
| 100 | 34.409 | 0.298 | 2.981 | 23.666 | 0.298 | 2.981 | 3.434 | 79.799 | 2.978 |
| 150 | 36.423 | 0.447 | 2.981 | 25.035 | 0.447 | 2.981 | 8.641 | 79.237 | 8.925 |
| 200 | 37.853 | 0.596 | 2.981 | 25.893 | 0.596 | 2.981 | 11.545 | 79.744 | 11.465 |
| 250 | 38.961 | 0.745 | 2.981 | 25.558 | 0.745 | 2.981 | 14.429 | 80.393 | 14.607 |
| 298.15 | 39.836 | 0.889 | 2.981 | 27.083 | 0.889 | 2.981 | 17.297 | 81.180 | 18.129 |
| 300 | 39.867 | 0.894 | 2.981 | 27.102 | 0.894 | 2.981 | 17.410 | 81.214 | 18.271 |
| 350 | 40.633 | 1.043 | 2.981 | 27.561 | 1.043 | 2.981 | 20.519 | 82.225 | 22.181 |
| 400 | 41.296 | 1.192 | 2.981 | 27.959 | 1.192 | 2.981 | 23.736 | 83.432 | 26.077 |
| 450 | 41.881 | 1.341 | 2.981 | 28.310 | 1.341 | 2.981 | 27.024 | 84.829 | 29.791 |
| 500 | 42.405 | 1.490 | 2.981 | 28.624 | 1.490 | 2.981 | 30.344 | 86.406 | 33.239 |
| 550 | 42.878 | 1.639 | 2.981 | 28.908 | 1.639 | 2.981 | 33.662 | 88.148 | 36.397 |
| 600 | 43.311 | 1.788 | 2.981 | 29.168 | 1.788 | 2.981 | 36.955 | 90.041 | 39.272 |
| 650 | 43.708 | 1.938 | 2.981 | 29.406 | 1.938 | 2.981 | 40.203 | 92.071 | 41.888 |
| 700 | 44.076 | 2.087 | 2.981 | 29.627 | 2.087 | 2.981 | 43.396 | 94.226 | 44.272 |
| 750 | 44.419 | 2.236 | 2.981 | 29.833 | 2.236 | 2.981 | 46.526 | 96.495 | 46.449 |
| 800 | 44.740 | 2.385 | 2.981 | 30.025 | 2.385 | 2.981 | 49.588 | 98.868 | 48.442 |
| 850 | 45.041 | 2.534 | 2.981 | 30.206 | 2.534 | 2.981 | 52.580 | 101.336 | 50.272 |
| 900 | 45.325 | 2.683 | 2.981 | 30.376 | 2.683 | 2.981 | 55.502 | 103.893 | 51.956 |
| 950 | 45.594 | 2.832 | 2.981 | 30.537 | 2.832 | 2.981 | 58.354 | 106.530 | 53.508 |
| 1000 | 45.848 | 2.981 | 2.981 | 30.690 | 2.981 | 2.981 | 61.135 | 109.242 | 54.941 |
Unit for St , Sr, Sv , Ct , Cr and Cv is Cal/Mol-Kelvin; Unit for Et , Er and Ev is KCal/Mol
Table 5: Participation of S, E and Cv for the various motions at different temperature

The rotational component that will take part in entropy (Sr) through the respective partition function (qr) can be comprehend from the following equation,

Similarly, the entropy by vibrational motion (Sv) includes the definition as,

The comparative plot of St, Sr and Sv against different temperature reports the interesting trend of behavior which is shown in Figure 10. When temperature is about 100 K then the entropy follows St>Sr>Sv order. But while the temperature gradually increases from 100 K to 1000 K, Sv>St>Sr trend is noticed which indicates significant change or increase in entropy contributed by vibrational motion. These results concluded that though the initial entropy of MDOL is supported by translational and rotational motion but at the higher temperature (above 750 K) the entropy is largely enhanced by vibrational motion.
The E, due to translational (Et) and rotational (Er) contribution can be described as,


The Et and Er values for various temperature demonstrate to be gradual equal increase. It is evident the same from Table 5 and illustrated in Figure 11, respectively.
And the internal energy favour by vibration (Ev) motions is high even for 100 K and increases till 1000 K. This denotes that the internal energy of MDOL is largely sustained by vibrational motion. The Ev can be expressed by,

Unlike the S and E, the Cv must be derived from the E of respective motion rather than partition functions. The Cv on the ground of translational, rotational and vibrational motion can be presented as,


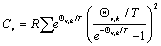
From Figure 12 and Table 5 the Ct and Cr values for MDOL is same for 100 - 1000 K of temperature. Since the value is about 2.981 Kcal/ Mol, there is no any significant trend is observed. But as like E and S the Cv is amplified by vibrational motion. Since the Cv is derived from E, the trend of E against various temperature is reflected in the behaviour of Cv as well.
Magnetic susceptibility
Atoms, molecules and free radicals or ions which contain one or more unpaired electron will possess permanent magnetic dipole moment that arises from the residual spin and angular momentum of the unpaired electrons. All substances having permanent magnetic moment display paramagnetic behaviour in nature. When a paramagnetic substance is placed in a magnetic field, they will align themselves in the direction of the field and thus produces positive magnetic susceptibility, which depends on the temperature; since thermal agitation will oppose the alignment of the magnetic dipoles. The effectiveness of the field diminishes with increase in temperature. The magnetic susceptibility (χm) of the molecules for various temperatures are predicted with knowledge of unpaired electron [58] and presented in Table 6. The corresponding fitting equation and the correlation graph between magnetic susceptibility (χm) and Temperature-1 (1/T) is shown in Figure 13. The effective magnetic moment is found to be a constant, which is 1.7864 × 10-5 (BM) and the Curie constant is obtained from the magnetic moment (μm) and is found to be 3 × 10-4.
| Temperature | 1/ Temperature | Magnetic susceptibility |
|---|---|---|
| 100 | 0.010 | 2.642E-06 |
| 150 | 0.007 | 1.761E-06 |
| 200 | 0.005 | 1.321E-06 |
| 250 | 0.004 | 1.057E-06 |
| 298.5 | 0.003 | 8.850E-07 |
| 300 | 0.003 | 8.806E-07 |
| 350 | 0.003 | 7.548E-07 |
| 400 | 0.003 | 6.605E-07 |
| 450 | 0.002 | 5.871E-07 |
| 500 | 0.002 | 5.284E-07 |
| 550 | 0.002 | 4.803E-07 |
| 600 | 0.002 | 4.403E-07 |
| 650 | 0.002 | 4.064E-07 |
| 700 | 0.001 | 3.774E-07 |
Table 6: Magnetic susceptibility of 2-methoxy-1,3-dioxolane by B3LYP/6-311+ +G(d,p).
Frontier molecular orbitals
To explain several types of reactions and for predicting the most reactive position in conjugated systems, molecular orbital and their properties such as energy are used [59]. The highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are the most important orbital in a molecule. The eigen values of HOMO and LUMO and their energy gap reflect the biological activity of the molecule. A molecule having a small frontier orbital gap is more polarizable and is generally associated with a high chemical reactivity and low kinetic stability [60,61]. HOMO, which can be thought of the outer orbital containing electrons, tends to give these electrons as an electron donor and hence the ionization potential is directly related to the energy of the HOMO. On the other hand, LUMO can accept electrons and the LUMO energy is directly related to electron affinity [62]. The energies of HOMO and LUMO and their orbital energy gap are calculated by B3LYP/6-311++G(d,p) method and the pictorial illustration of their HOMO-LUMO distribution and their respective positive and negative region are shown in Figure 14. The positive and negative phase is represented in red and green colour, respectively. For understanding various aspects of pharmacological sciences including drug design and the possible eco-toxicological characteristics of the drug molecules, several new chemical reactivity descriptors have been proposed. Conceptual DFT based descriptors have helped in many ways to understand the structure of molecules and their reactivity by calculating the chemical potential, global hardness and electrophilicity. Using HOMO and LUMO orbital energies, the ionization energy and electron affinity can be expressed as: I=-EHOMO, A=-ELUMO, ɳ=(-EHOMO + ELUMO) / 2 and μ=1/2 (EHOMO + ELUMO) [63]. Parr et al. [64] proposed the global electrophilicity power of a ligand as ω=μ2/2ɳ. This index measures the stabilization in energy when the system acquires an additional electronic charge from the environment. Electrophilicity encompasses both the ability of an electrophile to acquire additional electronic charge and the resistance of the system to exchange electronic charge with the environment. It contains information about both electron transfer (chemical potential) and stability (hardness) and is a better descriptor of global chemical reactivity. The hardness ɳ=(I-A)/2 and μ=- (I+A)/2, where I and A are the first ionization potential and electron affinity of the chemical species [65]. For the title compound, EHOMO=-7.1961 eV, ELUMO=-1.2588 eV, energy gap=HOMO-LUMO=5.9373 eV, ionization potential I=7.1961 eV, electron affinity A=1.2588 eV, global hardness ɳ=2.9686 eV, chemical potential μ=-4.2274 eV, global electrophilicity ω=3.01 eV. It is seen that the chemical potential of the title compound is negative and it means that the compound is stable. They do not decompose spontaneously into the elements they are made up of. The hardness signifies the resistance towards the deformation of electron cloud of chemical systems under small perturbation encountered during chemical process. The principle of hardness works in Chemistry and Physics but it is not physical observable. Soft systems are large and highly polarizable, while hard systems are relatively small and much less polarizable.
Total, partial, and overlap population density-of-states
In the boundary region, neighbouring orbitals may show quasi degenerate energy levels. In such cases, consideration of only the HOMO and LUMO may not yield a realistic description of the frontier orbitals. For this reason, the total density of states (TDOS), partial density of states (PDOS), and overlap population density of states (OPDOS) or crystal orbital overlap population (COOP) density of states [66-68], in terms of Mulliken population analysis were calculated and created by convoluting the molecular orbital information with Gaussian curves of unit height and full width at half maximum (FWHM) of 0.3 eV by using the GaussSum2.2 program [69]. The TDOS, PDOS and OPDOS of MDOL are plotted in Figures 15-17, respectively. They provide a pictorial representation of molecular orbital (MO) compositions and their contributions to chemical bonding. The most important application of the DOS plots is to demonstrate MO compositions and their contributions to the chemical bonding through the OPDOS plots which are also referred in the literature as COOP diagrams. The bonding, anti-bonding and nonbonding nature’s of the interaction of the two orbitals, atoms or groups are shown by OPDOS diagram. A positive value of the OPDOS indicates a bonding interaction (because of the positive overlap population), whereas negative value indicates that there is an anti-bonding interaction (due to negative overlap population) and zero value indicates nonbonding interactions [70]. Additionally, the OPDOS diagrams allow us to determine and compare the donor-acceptor properties of the ligands and ascertain the bonding and non-bonding. The PDOS plot mainly presents the composition of the fragment orbitals contributing to the molecular orbitals which are seen from Figure 16. As seen Figure 16, HOMO orbitals are localized on the ring (C3H5O2) and methoxy (OCH3) group, their contributions about 59% and 41%, respectively. Similarly, the LUMO orbitals are localized on the ring (C3H5O2) (78%) and methoxy (OCH3) group (22%) of the compound. However to have information about bonding and anti-bonding properties is very hard according to percentage sharing of atomic orbitals or molecular fragments in the molecule. Therefore OPDOS diagram (some of its orbitals of energy values of interaction between selected groups) is shown on the figure easily, ring ↔ methoxy group (blue line) system is positive and negative (bonding and antibonding interaction). As can be seen from the OPDOS plot, the MDOL have bonding and anti-bonding character both HOMO and LUMO.
Reduced density gradient (RDG)
Johnson et al. [71] published an approach to investigate a weak interactions in real space based on the electron density and its derivatives called Reduced density gradient (RDG) is dimensionless quantity defined as, following:

The region with low electron density and low RDG value obtained density and its first derivative, indicate weak interactions. To learn about the interaction in more detail, the sign of λ2 is used to distinguish the bonded (λ2<0) from non-bonded (λ2>0) interactions. The sign of λ2 multiplied electron density ρ obtained the plots of RDG versus permit to investigate and visualize of a wide range of interactions types. The RDG calculations are performed by Multiwfn program [72] and plotted by VMD program [73], respectively. The RDG versus sign (λ2)ρ (electron density value) peaks provide information about the strength of interaction. There is one spike in the low-density, low gradient region as seen Figure 18, indicative of strong repulsion positive values of sign (λ2)ρ.
Large, positive values of sign (λ2)ρ are indicated that strong repulsion interactions and negative ones indicates stronger attractive interactions. The strength of weak interactions have positive correlations with electron density ρ in corresponding region, Van der Waals (VdW) interaction regions always have very small ρ, while the regions correspond to strong steric effect and hydrogen bond always have relative large ρ. The regions are identified by color as different type seen from Figure 19. The color from blue to red means from stronger attraction to repulsion, respectively. The center of ring for MDOL molecule shows that strong steric effect, filled by red color. And VdW interactions identified by green or light brown color, between ring and methoxy group for MDOL.
Natural bond orbital (NBO) analysis
The natural bond orbital analysis (NBO) unlock the secrets about stability, bonding, intramolecular charge transfer (ICT) and donoracceptor relationship which are all collectively contribute to determine the electronic structure property of the title compound MDOL. The question on MDOL molecular stabilization can be answered by second order perturbation theory analysis. The stabilization interaction energy [74] can be mathematically expressed as below.

The donor, acceptor stabilisation interaction is often influenced by numerator and denominator terms involved in the given equation. The amplification of stabilisation energy is reciprocally related with ΔE. The ΔE can be expressed as ΔE=E(j)-E(i) where E(j) and E(i) denotes orbital energies of non-Lewis and Lewis orbitals [75]. The |Fij| represents cooperating element. As the NBO algorithm calculates all possible donor acceptor combinations [76], several significant interactions have been given in Table 7. The pictorial projections of selected thirteen donors, acceptors and their stabilizing interactions have been shown in Figure 20 based on descending interaction stabilization energy. Though several types of electronic interactions available between bonding, non-bonding and anti-bonding orbitals, the prominent stabilization includes lone pair (LP) to π* and π to π* transition in MDOL. The highest stabilization about 56.02 kJ mol-1 is observed at the interaction between LP(2) O3 → π* (C2-O7). The π → π* type of transition was observed in twelfth and thirteenth interaction. The twelfth interaction holds 12.43 kJ mol-1 of stabilization energy whereas the thirteenth interaction bear 11.55 kJ mol-1. The stabilization energy difference between these two interactions was 0.88 kJ mol-1.
| Donor (i) | Orbital energy E(i) a.u | Acceptor (j) | Orbital energy E(j) a.u | E(2)a(kJ mol-1) | E(j)-E(i)b(a.u) | F(i,j)c(a.u) |
|---|---|---|---|---|---|---|
| LP(2) O3 | 1.90851 | π* (C2-O7) | 0.08655 | 56.02 | 0.61 | 0.081 |
| LP(2) O7 | 1.89887 | π* (C2-O7) | 0.08655 | 55.73 | 0.61 | 0.081 |
| LP(2) O7 | 1.90462 | π* (C2-O3) | 0.07773 | 54.68 | 0.59 | 0.079 |
| LP(2) O1 | 1.89887 | π* (C5-H15) | 0.02459 | 29.83 | 0.7 | 0.064 |
| LP(2) O7 | 1.90462 | π* (C8-H9) | 0.01916 | 26.90 | 0.7 | 0.061 |
| LP(2) O3 | 1.90851 | π* (C4-H13) | 0.01960 | 22.22 | 0.7 | 0.055 |
| LP(2) O7 | 1.90462 | π* (C2-H6) | 0.04614 | 21.38 | 0.68 | 0.053 |
| LP(2) O7 | 1.90462 | π* (C8-H11) | 0.01963 | 21.30 | 0.68 | 0.054 |
| LP(2) O1 | 1.89887 | π* (C2-O3) | 0.07773 | 20.42 | 0.6 | 0.048 |
| LP(2) O3 | 1.90851 | π* (C4-H12) | 0.02186 | 19.96 | 0.7 | 0.052 |
| LP(1) O7 | 1.95665 | π* (O1-C2) | 0.04828 | 17.61 | 0.88 | 0.054 |
| π (C2-H6) | 1.98000 | π* (O1-C5) | 0.01903 | 12.43 | 0.82 | 0.044 |
| π (C8-H10) | 1.99214 | π* (C2-O7) | 0.08655 | 11.55 | 0.82 | 0.043 |
aStabilisation (delocalisation) energy.
bEnergy difference between i (donor) and j (acceptor) NBO orbitals.
cF(i,j) means the Fock matrix element between i and j orbitals.
Table 7: Second order perturbation theory analysis of Fock matrix in NBO basis for 2-methoxy-1,3-dioxolane by B3LYP/6-311++G(d,p).
Topological parameters
The charge density distribution of the molecules can be determined from the wave function using Bader’s Quantum Theory of Atoms in Molecules (QTAIM) [77], which are very useful to understand the nature of chemical bonds, reactivity and stability of molecular systems. Also, it provides the essential bond topological properties of the electron density ρbcp(r) at the bond critical point, where ∇ρ (r ) = 0 . The critical point of molecule can be classified according to its rank(ω) and signature(σ) [78]. The rank, ω of critical point is equal to the number of non-zero Eigen values of the Hessian matrix of ρbcp(r) and the signature, σ is the algebraic sum of the signs of the Eigen values. If the Eigen values are positive, its associated Eigen vector or gradient path originates at, and is directed away from the critical point. For negative Eigen value the gradient path terminates at, and is directed towards the critical point. Among the four type of non-degenerate critical points; (3,-3) nucleus critical point, (3,+3) cage critical point, (3,+1) ring critical point, and (3,-1) bond critical point, only the (3,-1) type of bond critical points (bcp’s) were considered in this study. The wave function obtained from the optimization is used to calculate the bond topological properties at the bcp’s using the Bader’s theory of AIM implemented in AIMPAC software [79]. The topological parameters; electron density, Laplacian of electron density, ellipticity, Eigen values and energy density values for all the (3,-1) critical points have been investigated and presented in Table 8.
| Bonds | ρbcp(r)a | ∇2ρbcp(r)b | εc | λ1d | λ2d | λ3d | d1e | d2e | Df | G(r)g | V(r)g | H(r)g |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O1 - C2 | 1.956 | -17.053 | 0.033 | -15.050 | -14.565 | 12.562 | 0.496 | 0.891 | 1.387 | 1.505 | -4.204 | -2.699 |
| C2 - O3 | 1.841 | -15.811 | 0.041 | -13.638 | -13.106 | 10.933 | 0.896 | 0.519 | 1.414 | 1.273 | -3.653 | -2.380 |
| O3 - C4 | 1.657 | -10.949 | 0.015 | -10.497 | -10.344 | 9.891 | 0.924 | 0.515 | 1.439 | 1.317 | -3.400 | -2.083 |
| O1 - C5 | 1.672 | -10.826 | 0.021 | -10.606 | -10.383 | 10.164 | 0.925 | 0.511 | 1.436 | 1.368 | -3.494 | -2.126 |
| C4 - C5 | 1.666 | -13.696 | 0.042 | -11.644 | -11.177 | 9.124 | 0.770 | 0.767 | 1.537 | 0.371 | -1.702 | -1.330 |
| C2 - H6 | 1.971 | -25.067 | 0.003 | -19.746 | -19.695 | 14.373 | 0.718 | 0.362 | 1.080 | 0.197 | -2.149 | -1.952 |
| C2 - O7 | 1.876 | -16.089 | 0.124 | -14.676 | -13.061 | 11.647 | 0.894 | 0.509 | 1.403 | 1.357 | -3.840 | -2.483 |
| O7 - C8 | 1.679 | -9.729 | 0.011 | -10.584 | -10.473 | 11.328 | 0.499 | 0.927 | 1.425 | 1.498 | -3.676 | -2.179 |
| C8 - H9 | 1.897 | -23.065 | 0.040 | -18.414 | -17.713 | 13.062 | 0.375 | 0.705 | 1.080 | 0.251 | -2.116 | -1.866 |
| C8 - H10 | 1.912 | -23.589 | 0.040 | -18.671 | -17.954 | 13.036 | 0.374 | 0.701 | 1.075 | 0.246 | -2.144 | -1.898 |
| C8 - H11 | 1.868 | -22.392 | 0.041 | -17.866 | -17.157 | 12.631 | 0.703 | 0.381 | 1.084 | 0.260 | -2.087 | -1.827 |
| C4 - H12 | 1.913 | -23.480 | 0.036 | -18.601 | -17.963 | 13.084 | 0.703 | 0.376 | 1.079 | 0.247 | -2.137 | -1.890 |
| C4 - H13 | 1.910 | -23.439 | 0.033 | -18.549 | -17.955 | 13.065 | 0.375 | 0.703 | 1.078 | 0.247 | -2.134 | -1.888 |
| C5 - H14 | 1.921 | -23.806 | 0.031 | -18.759 | -18.190 | 13.143 | 0.702 | 0.373 | 1.075 | 0.241 | -2.148 | -1.907 |
| C5 - H15 | 1.915 | -23.491 | 0.033 | -18.653 | -18.058 | 13.219 | 0.374 | 0.705 | 1.079 | 0.245 | -2.135 | -1.890 |
aElectron density (eÅ-3);bLaplacian of Electron density (eÅ-5);cBond ellipticity; dHessian eigen values (eÅ-5); eDistance between the critical point and respective bonded atomic nucleus (Å); fTotal bond path length (Å);gEnergy density (HÅ-3)
Table 8: Bond topological properties of 2-methoxy-1,3-dioxolane molecule.
The Laplacian of electron density bear the chemical significance. If  the charges are locally concentrated, the interaction is a open-shell type interaction and if
the charges are locally concentrated, the interaction is a open-shell type interaction and if  the charges are locally depleted and the atomic interaction is a closed-shell type interaction. It is much more valid when the Laplacian of electron density is correlated with local total energy density H(r) [80], which facilitates for the identification of strong and weak bonds in the molecule. The local total energy density is defined as
the charges are locally depleted and the atomic interaction is a closed-shell type interaction. It is much more valid when the Laplacian of electron density is correlated with local total energy density H(r) [80], which facilitates for the identification of strong and weak bonds in the molecule. The local total energy density is defined as
H(r)=G(r)+V(r)
where G(r) and V(r) are the local kinetic and potential energy density. V(r) is always negative and G(r) is positive; the sign of H(r) indicates the dominant one in the bonding regions.
From the Laplacian of electron density values it is clear that the O7-C8 bond is depleted in nature, since it Laplacian of electron density gives a lesser negative value (-9.729). Whereas the highly concentrated bonds are found to be C-H bonds. Apart from these bonds, the Laplacian of electron density corresponds to C4-C5 bond in the molecule is found to be -13.696 eÅ-5, revealing that the C4-C5 bond is lesser concentrated compared to the C-H bonds. The total energy density H(r) for the C4-C5 bond is -1.330 HÅ-3, this value is found to be very small on compared with all other bonds in the molecule, indicates, the weakness of C4-C5 bond in MDOL molecule.
The bond ellipticity [81], ε=[(λ1/λ2) -1] is defined as the measure of anisotropy of electron distribution at BCP, where λ1 and λ2 are the negative Eigen values of Hessian matrix. The high ellipticity value indicates the large anisotropy of bonding density ρbcp(r) and hence a strong deviation from σ-type bond character. The ellipticity of C2-H6 bond is found to be small; it indicates that the bond density is highly isotropic. The large ellipticity value is occurred in C2-O7 bond, it shows that the C2-O7 bond density is highly anisotropic.
The complete molecular structural parameters, fundamental vibrational frequencies and thermodynamic properties of the optimized geometry of MDOL have been reported for the first time using DFT calculations. The computed geometrical parameters are compared with the observed X-Ray diffraction data of similar compound. Theoretical 1H and 13C NMR chemical shift values (with respect to TMS) are reported and compared with experimental data, showing a very good agreement both 1H and 13C NMR. Theoretical UV-Visible spectrum for various solvents is discussed. In the case of solvents, the peaks are somewhat shifted slightly to the lower wavelengths resulting the influence of solvent effect on the title molecule. The frontier molecular orbital have been visualized and the HOMO-LUMO energy gap has been calculated. The lesser value of HOMO-LUMO energy gap has substantial influence on the bioactivity of the molecule. The electronic stabilization of MDOL was understood by NBO analysis by means of Donor and Acceptor orbital interactions producing hierarchy of stabilization energy. The topological analysis based on the AIM theory shows the difference of charge distribution in all bonds. The proceedings on thermodynamic analysis draw the attention by its trend fastidiously the behavior between temperature and entropy (S), internal energy (E) and heat capacity (Cv) with constant volume. The overall computational spectral analysis, electronic structure calculations, thermodynamic and magnetic properties on MDOL leaves the legacy and open up the way to extend its application in the field of pharmaceutical discipline and molecular drug designing.