Journal of Theoretical & Computational Science
Open Access
ISSN: 2376-130X
ISSN: 2376-130X
Research Article - (2014) Volume 1, Issue 2
In the present methodical study, FT-IR and FT-Raman of the 2,4,6-Nitrophenol (TNP) called as picric acid are recorded and the observed vibrational frequencies are assigned. The hybrid computational calculations are carried out by HF and DFT (B3LYP and B3PW91) methods with 6-31+G(d,p) and 6-311++G(d,p) basis sets and the corresponding results are tabulated. The alternation of structure of nitro phenol due to the subsequent substitutions of NO2 is investigated. The vibrational sequence pattern of the molecule related to the substitutions is analyzed. Moreover, 13C NMR and 1H NMR are calculated by using the gauge independent atomic orbital (GIAO) method with B3LYP methods and the 6-311++G(d,p) basis set and their spectra are simulated and the chemical shifts related to TMS are compared. A study on the electronic properties; absorption wavelengths, excitation energy, dipole moment and frontier molecular orbital energies, are performed by HF and DFT methods. The calculated HOMO and LUMO energies and the kubo gap analysis show that the occurring of charge transformation within the molecule. Besides frontier molecular orbitals (FMO), molecular electrostatic potential (MEP) was performed. NLO properties related to Polarizability and hyperpolarizability are also discussed. The thermodynamic properties (thermal energy, heat capacity and entropy) of the title compound are calculated in gas phase and are interpreted with different types of phenols.
<Keywords: 2,4,6-Nitrophenol, Picric acid, First order hyperpolarizability, Vibrational sequence pattern, Chemical shifts, Frontier molecular orbital energies
The aromatic systems in conjugated with nitro group leading to charge transfer systems, have been intensely studied and their crystals are highly recognized as the materials of the future because their molecular nature combined with versatility of synthetic chemistry can be used to alter their structure in order to maximize the non-linear properties [1-4]. The nitro substituted phenols with high optical nonlinearities are very promising materials for future optoelectronic and non-linear optical applications. The optical transparency of this crystal is quite good and hence it can be a potential material for frequency replication in electro-optic modulation, frequency conversion and THz wave generation of non-linear optics [5,6].
Phenol derivatives are interesting molecules for theoretical studies due to their relatively small size and similarity to biological species. The phenols are organic compounds that contain a hydroxyl group (OH) bound directly to a carbon atom in the benzene ring. The phenol materials with very large second-order nonlinear optical (NLO) susceptibilities have attracted a lot of attention because of their potential applications in electro-optic modulation. The material of phenols with more nitro groups having the properties of large secondorder optical nonlinearities, short transparency cut-off wavelength and stable physiochemical performance which are needed in the realization of most of the recent electronic applications. The 2,4,6-Trinitrophenol (TNP), generally known as picric acid, is a nonlinear optical crystal and a well-known organic NLO crystal by its shorter cutoff wavelength, optical quality, sufficiently large nonlinear coefficient, transparency in UV region and high damage threshold [7,8].
The compound 2,4,6-Trinitrophenol (Picric acid) is purchased from Sigma–Aldrich Chemicals, USA, which is of spectroscopic grade and hence used for recording the spectra as such without any further purification. The FT-IR spectrum of the compound is recorded in Bruker IFS 66V spectrometer in the range of 4000–400 cm−1. The spectral resolution is ± 2 cm−1. The FT-Raman spectrum of same compound is also recorded in the same instrument with FRA 106 Raman module equipped with Nd: YAG laser source operating at 1.064 μm line widths with 200 mW power. The spectra are recorded in the range of 4000-100 cm−1 with scanning speed of 30 cm−1 min−1 of spectral width 2 cm−1. The frequencies of all sharp bands are accurate to ± 1 cm−1.
In the present work, HF and some of the hybrid methods; B3LYP and B3PW91 are carried out using the basis sets 6-31+G(d,p) and 6-311+G(d,p). All these calculations have been carried out using GAUSSIAN 09W [9] program package on Pentium IV processor in personal computer. In DFT methods; Becke’s three parameter hybrids function combined with the Lee-Yang-Parr correlation function (B3LYP) [10,11], Becke’s three parameter exact exchange-function (B3) [12] combined with gradient-corrected correlational functional of Lee, Yang and Parr (LYP) [13,14] and Perdew and Wang (PW91) [15,16] predict the best results for molecular geometry and vibrational frequencies for moderately larger molecules. The calculated frequencies are scaled down to yield the coherent with the observed frequencies. The scaling factors are 0.88 and 0.903 for HF/6-31+G/6-311++G(d,p) method. For B3LYP/6-311++G (d,p) basis set, the scaling factors are 0.980, 0.907, 0.955 and 1.02/0.920, 0.975 and 1.02. For B3PW91/6- 31+G/6-311+G (d,p) basis set, the scaling factors are 0.930,0.906, 0.955 and 1.02/0.910, 0.955, 0.982 and 1.02. The optimized molecular structure of the molecule is obtained from Gaussian 09 and Gauss view program and is shown in Figure 1. The comparative optimized structural parameters such as bond length, bond angle and dihedral angle are presented in Table 1. The observed (FT-IR and FT-Raman) and calculated vibrational frequencies and vibrational assignments are submitted in Table 2. Experimental and simulated spectra of IR and Raman are presented in the Figures 2 and 3, respectively.
| Geometrical Parameters | Methods | Experimental Value | ||||
|---|---|---|---|---|---|---|
| HF | B3LYP | B3PW91 | ||||
| 6-311G (d, p) | 6-31G (d, p) | 6-311G (d, p) | 6-31G (d, p) | 6-311G (d, p) | ||
| Bond length (Å) | ||||||
| C1-C2 | 1.408 | 1.420 | 1.416 | 1.418 | 1.414 | 1.392 |
| C1-C6 | 1.410 | 1.426 | 1.423 | 1.424 | 1.420 | 1.406 |
| C1-O18 | 1.299 | 1.315 | 1.315 | 1.310 | 1.310 | 1.357 |
| C2-C3 | 1.371 | 1.382 | 1.379 | 1.380 | 1.377 | 1.402 |
| C2-N9 | 1.458 | 1.475 | 1.482 | 1.470 | 1.475 | 1.451 |
| C3-C4 | 1.385 | 1.394 | 1.391 | 1.392 | 1.389 | 1.384 |
| C3-H7 | 1.071 | 1.082 | 1.081 | 1.083 | 1.082 | 1.080 |
| C4-C5 | 1.371 | 1.383 | 1.380 | 1.381 | 1.378 | 1.387 |
| C4-N12 | 1.451 | 1.469 | 1.477 | 1.464 | 1.471 | 1.451 |
| C5-C6 | 1.384 | 1.391 | 1.389 | 1.389 | 1.386 | 1.383 |
| C5-H8 | 1.070 | 1.082 | 1.080 | 1.083 | 1.082 | 1.080 |
| C6-N15 | 1.449 | 1.457 | 1.465 | 1.451 | 1.458 | 1.451` |
| N9-O10 | 1.194 | 1.229 | 1.222 | 1.224 | 1.216 | 1.225 |
| N9-O11 | 1.186 | 1.224 | 1.216 | 1.218 | 1.211 | 1.217 |
| N12-O13 | 1.192 | 1.228 | 1.221 | 1.223 | 1.215 | 1.225 |
| N12-O14 | 1.191 | 1.228 | 1.221 | 1.222 | 1.215 | 1.217 |
| N15-O16 | 1.183 | 1.219 | 1.212 | 1.214 | 1.206 | 1.225 |
| N15-O17 | 1.206 | 1.251 | 1.243 | 1.245 | 1.238 | 1.217 |
| O17-H19 | 1.782 | 1.646 | 1.676 | 1.625 | 1.649 | - |
| O18-H19 | 0.953 | 0.994 | 0.987 | 0.995 | 0.989 | 0.820 |
| Bond angle (°) | ||||||
| C2-C1-C6 | 115.84 | 115.83 | 115.72 | 115.77 | 115.64 | - |
| C2-C1-O18 | 119.31 | 120.82 | 120.34 | 120.97 | 120.55 | - |
| C6-C1-O18 | 124.80 | 123.31 | 123.91 | 123.22 | 123.77 | - |
| C1-C2-C3 | 122.49 | 122.08 | 122.34 | 122.09 | 122.35 | - |
| C1-C2-N9 | 120.81 | 121.03 | 120.66 | 121.01 | 120.65 | - |
| C3-C2-N9 | 116.69 | 116.87 | 116.99 | 116.88 | 116.98 | - |
| C2-C3-C4 | 119.18 | 119.41 | 119.25 | 119.44 | 119.28 | - |
| C2-C3-H7 | 120.03 | 119.92 | 120.12 | 119.90 | 120.09 | - |
| C4-C3-H7 | 120.77 | 120.66 | 120.62 | 120.65 | 120.61 | - |
| C3-C4-C5 | 121.13 | 121.47 | 121.41 | 121.45 | 121.38 | - |
| C3-C4-N12 | 119.43 | 119.29 | 119.31 | 119.29 | 119.32 | - |
| C5-C4-N12 | 119.43 | 119.22 | 119.26 | 119.25 | 119.28 | - |
| C4-C5-C6 | 119.10 | 118.67 | 118.77 | 118.63 | 118.73 | - |
| C4-C5-H8 | 120.82 | 120.97 | 120.95 | 120.98 | 120.97 | - |
| C6-C5-H8 | 120.06 | 120.35 | 120.26 | 120.37 | 120.28 | - |
| C1-C6-C5 | 122.20 | 122.50 | 122.46 | 122.58 | 122.55 | - |
| C1-C6-N15 | 120.85 | 120.19 | 120.28 | 120.08 | 120.15 | - |
| C5-C6-N15 | 116.94 | 117.30 | 117.25 | 117.32 | 117.28 | - |
| C2-N9-O10 | 116.22 | 116.35 | 116.29 | 116.31 | 116.26 | - |
| C2-N9-O11 | 117.98 | 117.81 | 117.52 | 117.67 | 117.41 | - |
| O10-N9-O11 | 125.75 | 125.80 | 126.15 | 125.98 | 126.30 | - |
| C4-N12-O13 | 117.29 | 117.24 | 117.18 | 117.17 | 117.12 | - |
| C4-N12-O14 | 117.16 | 117.17 | 117.07 | 117.08 | 117.00 | - |
| O13-N12-O14 | 125.53 | 125.58 | 125.74 | 125.73 | 125.87 | - |
| C6-N15-O16 | 118.16 | 118.95 | 118.84 | 118.99 | 118.91 | - |
| C6-N15-O17 | 117.89 | 117.87 | 117.54 | 117.72 | 117.41 | - |
| O16-N15-O17 | 123.93 | 123.17 | 123.60 | 123.28 | 123.66 | - |
| C1-O18-H19 | 110.76 | 106.52 | 107.05 | 106.08 | 106.42 | - |
| Dihedral angles (°) | ||||||
| C6-C1-C2-C3 | 1.466 | 1.3076 | 1.149 | 0.8878 | 1.151 | - |
| C6-C1-C2-N9 | -178.32 | -178.85 | -178.77 | -178.8 | -178.7 | - |
| O18-C1-C2-C3 | -176.45 | -177.36 | -177.18 | -177.3 | -177.1 | - |
| O18-C1-C2-N9 | 3.7576 | 2.9185 | 2.8913 | 2.9281 | 2.925 | - |
| C2-C1-C6-C5 | -0.0635 | 0.3338 | 0.1648 | 0.3803 | 0.219 | - |
| C2-C1-C6-N15 | -179.74 | -179.53 | -179.55 | -179.4 | -179.5 | - |
| O18-C1-C6-C5 | 177.72 | 178.516 | 178.428 | 178.54 | 178.46 | - |
| O18-C1-C6-N15 | -1.955 | -1.3538 | -1.2911 | -1.331 | -1.27 | - |
| C2-C1-O18-H19 | 178.52 | 178.269 | 178.052 | 178.21 | 178.04 | - |
| C6-C1-O18-H19 | 0.8105 | 0.1744 | -0.1351 | 0.1478 | -0.117 | - |
| C1-C2-C3-C4 | -2.032 | -1.5772 | -1.8541 | -1.662 | -1.923 | - |
| C1-C2-C3-H7 | 178.18 | 178.319 | 177.900 | 178.24 | 177.89 | - |
| N9-C2-C3-C4 | 177.76 | 178.152 | 178.075 | 178.10 | 178.00 | - |
| N9-C2-C3-H7 | -2.014 | -1.9507 | -2.1694 | -1.990 | -2.181 | - |
| C1-C2-N9-O10 | -145.8 | -152.28 | -146.70 | -151.8 | -146. | - |
| C1-C2-N9-O11 | 36.250 | 29.2751 | 35.0592 | 29.729 | 35.55 | - |
| C3-C2-N9-O10 | 34.382 | 27.9808 | 33.3687 | 28.386 | 33.86 | - |
| C3-C2-N9-O11 | -143.5 | -150.45 | -144.87 | -150.0 | -144.3 | - |
| C2-C3-C4-C5 | 1.1688 | 1.0898 | 1.2392 | 1.178 | 1.3193 | - |
| C2-C3-C4-N12 | -178.9 | -179.13 | -179.09 | -179.0 | -179.0 | - |
| H7-C3-C4-C5 | -179.0 | -178.80 | -178.51 | -178.7 | -178.4 | - |
| H7-C3-C4-N12 | 0.8001 | 0.9706 | 1.1482 | 1.0071 | 1.1373 | - |
| C3-C4-C5-C6 | 0.1782 | 0.0726 | 0.026 | 0.0477 | 0.0006 | - |
| C3-C4-C5-H8 | 179.71 | 179.675 | 179.622 | 179.63 | 179.58 | - |
| N12-C4-C5-C6 | -179.6 | -179.70 | -179.63 | -179.6 | -179.6 | - |
| N12-C4-C5-H8 | -0.132 | -0.1012 | -0.0404 | -0.105 | -0.052 | - |
| C3-C4-N12-O13 | -179.4 | -179.51 | -179.32 | -179.4 | -179.2 | - |
| C3-C4-N12-O14 | 0.5989 | 0.4985 | 0.6989 | 0.527 | 0.747 | - |
| C5-C4-N12-O13 | 0.4134 | 0.266 | 0.3458 | 0.256 | 0.364 | - |
| C5-C4-N12-O14 | -179.5 | -179.71 | -179.63 | -179.7 | -179.6 | - |
| C4-C5-C6-C1 | -0.729 | -0.7932 | -0.7334 | -0.837 | -0.777 | - |
| C4-C5-C6-N15 | 178.96 | 179.080 | 178.994 | 179.03 | 178.96 | - |
| H8-C5-C6-C1 | 179.72 | 179.601 | 179.667 | 179.57 | 179.63 | - |
| H8-C5-C6-N15 | -0.582 | -0.5251 | -0.6049 | -0.547 | -0.615 | - |
| C1-C6-N15-O16 | -178.4 | -178.65 | -178.31 | -178.64 | -178.3 | - |
| C1-C6-N15-O17 | 1.6025 | 1.4008 | 1.7265 | 1.415 | 1.743 | - |
| C5-C6-N15-O16 | 1.8929 | 1.4677 | 1.9512 | 1.477 | 1.946 | |
| C5-C6-N15-O17 | -178.0 | -178.47 | -178.00 | -178.46 | -178.0 | |
Table 1: Optimized geometrical parameters for 2,4,6-Nitrophenol computed at HF/DFT(B3LYP&B3PW91) with 6-31& 6-311G(d, p) basis sets.
| S.No | Symmetry Species CS | Observed Frequency (cm-1) FTIR FTRaman | Methods | Vibrational Assignments | |||||
|---|---|---|---|---|---|---|---|---|---|
| HF | B3LYP | B3PW91 | |||||||
| 6-31+G (d, p) | 6-311+G (d, p) | 6-31+G (d, p) | 6-311+G (d, p) | ||||||
| 1 | A’ | 3300w | - | 3295 | 3255 | 3327 | 3336 | 3292 | (O-H) υ |
| 2 | A’ | 2960vs | - | 2995 | 2959 | 2979 | 2957 | 2950 | (C-H) υ |
| 3 | A’ | 2950vs | - | 2988 | 2955 | 2975 | 2954 | 2946 | (C-H) υ |
| 4 | A’ | - | 1640vs | 1649 | 1665 | 1648 | 1648 | 1633 | (C=C) υ |
| 5 | A’ | - | 1630vs | 1634 | 1638 | 1619 | 1629 | 1610 | (C=C) υ |
| 6 | A’ | 1620vs | - | 1616 | 1622 | 1632 | 1617 | 1597 | (C=C) υ |
| 7 | A’ | 1550vs | - | 1552 | 1555 | 1548 | 1575 | 1564 | (N-O) υ as |
| 8 | A’ | 1540vs | - | 1540 | 1539 | 1531 | 1561 | 1551 | (N-O) υ as |
| 9 | A’ | - | 1475s | 1460 | 1455 | 1468 | 1474 | 1459 | (N-O) υ as |
| 10 | A’ | 1450vs | - | 1449 | 1452 | 1432 | 1426 | 1455 | (C-C) υ |
| 11 | A’ | - | 1445vs | 1447 | 1435 | 1448 | 1452 | 1440 | (C-C) υ |
| 12 | A’ | - | 1440vs | 1441 | 1427 | 1411 | 1455 | 1440 | (C-C) υ |
| 13 | A’ | 1420vs | - | 1420 | 1416 | 1398 | 1443 | 1429 | (N-O) υs |
| 14 | A’ | 1340w | 1340vs | 1324 | 1336 | 1351 | 1317 | 1344 | (N-O) υs |
| 15 | A’ | 1310vs | - | 1311 | 1309 | 1319 | 1292 | 1314 | (N-O) υs |
| 16 | A’ | 1250vs | - | 1206 | 1258 | 1250 | 1266 | 1290 | (O-H) δ |
| 17 | A’ | 1180m | - | 1185 | 1175 | 1187 | 1157 | 1180 | (C-H) δ |
| 18 | A’ | - | 1150vs | 1168 | 1154 | 1145 | 1119 | 1150 | (C-H) δ |
| 19 | A’ | 1090vs | 1094 | 1994 | 1091 | 1091 | 1090 | (C-N) υ | |
| 20 | A’ | 1085vs | 1085vs | 1048 | 997 | 995 | 993 | 991 | (C-N) υ |
| 21 | A’ | 950m | - | 991 | 947 | 960 | 923 | 945 | (C-N) υ |
| 22 | A’ | - | 940m | 959 | 937 | 950 | 919 | 938 | (C-O) υ |
| 23 | A" | - | 920vs | 941 | 914 | 931 | 903 | 928 | (C-H) γ |
| 24 | A" | 835m | - | 851 | 840 | 849 | 816 | 845 | (C-H) γ |
| 25 | A" | 830m | 830m | 828 | 837 | 840 | 809 | 830 | (O-H) γ |
| 26 | A’ | - | 800vs | 806 | 793 | 809 | 803 | 818 | (NO2) δ |
| 27 | A’ | - | 795s | 785 | 798 | 797 | 807 | 791 | (NO2) δ |
| 28 | A’ | 780vs | - | 768 | 160 | 760 | 782 | 770 | (NO2) δ |
| 29 | A’ | 740vs | 740s | 735 | 757 | 744 | 766 | 737 | (CCC) δ |
| 30 | A’ | 730vs | 730vs | 725 | 756 | 728 | 761 | 726 | (CCC) δ |
| 31 | A’ | 700vs | 700vs | 704 | 733 | 703 | 738 | 714 | (CCC) δ |
| 32 | A’ | - | 660w | 661 | 719 | 688 | 723 | 646 | (C-N) δ |
| 33 | A’ | 650w | - | 647 | 670 | 647 | 673 | 650 | (C-N) δ |
| 34 | A’ | 550w | 550w | 541 | 560 | 548 | 561 | 550 | (C-N) δ |
| 35 | A" | - | 530w | 525 | 858 | 533 | 516 | 533 | (NO2) γ |
| 36 | A" | 510w | - | 506 | 515 | 511 | 508 | 514 | (NO2) γ |
| 37 | A" | 420m | - | 435 | 461 | 410 | 433 | 408 | (NO2) γ |
| 38 | A" | 400m | 400m | 396 | 412 | 402 | 388 | 403 | (CCC) γ |
| 39 | A" | 360w | - | 372 | 390 | 349 | 365 | 363 | (CCC) γ |
| 40 | A" | 340m | 340w | 344 | 355 | 338 | 333 | 342 | (CCC) γ |
| 41 | A’ | 330w | - | 336 | 351 | 332 | 329 | 336 | (C-O) δ |
| 42 | A" | 320m | - | 322 | 333 | 321 | 312 | 323 | (C-N) γ |
| 43 | A" | 310m | 310w | 310 | 324 | 310 | 303 | 311 | (C-N) γ |
| 44 | A" | 200m | 200m | 198 | 207 | 198 | 195 | 199 | (C-N) γ |
| 45 | A" | 190w | - | 183 | 192 | 188 | 192 | 188 | (C-O) γ |
| 46 | A" | 150w | 150m | 154 | 158 | 150 | 148 | 153 | (C-N) γ |
| 47 | A" | 120w | - | 124 | 131 | 121 | 131 | 125 | (C-N) γ |
| 48 | A" | 110w | - | 88 | 101 | 97 | 102 | 96 | (C-OH) τ |
| 49 | A" | 105w | - | 53 | 62 | 60 | 62 | 60 | (NO2) τ |
| 50 | A" | 100w | 100w | 52 | 57 | 53 | 57 | 52 | (NO2) τ |
| 51 | A" | 90w | - | 49 | 46 | 51 | 46 | 51 | (NO2)τ |
VS – Very –Strong; S – Strong; m- Medium; w – weak; as- Asymmetric; s – symmetric; υ – stretching; δ- In plane bending; γ– out plane bending; τ – Twisting:
Table 2: Observed and HF/DFT (LSDA & B3LYP) with 6-31& 6-311G (d, p) level calculated vibrational frequencies of 2,4,6-Nitrophenol.
The 1H and 13C NMR isotropic shielding are calculated with the GIAO method [17] using the optimized parameters obtained from B3LYP/6-311++G(d,p) method. 13C isotropic magnetic shielding (IMS) of any X carbon atoms is made according to value 13C IMS of TMS, CSX=IMSTMS-IMSx. The 1H and 13C isotropic chemical shifts of TMS at B3LYP methods with 6-311++G(d,p) level using the IEFPCM method are calculated for 4-,2,4- and 2,4,6-Nitrophenols. The absolute chemical shift is found between isotropic peaks and the peaks of TMS [18].
The electronic properties, HOMO-LUMO energies, absorption wavelengths and oscillator strengths are calculated using B3LYP method of the time-dependent DFT (TD-DFT) [19,20], basing on the optimized structure in gas phase. Thermodynamic properties of three phenols at 298.15ºC have been calculated in gas phase using B3LYP/6- 311++G (d,p) method. Moreover, the dipole moment, nonlinear optical (NLO) properties, linear polarizabilities and first hyperpolarizabilities and chemical hardness have also been studied.
Molecular geometry
The molecular structure of TNP belongs to CS point group symmetry is studied. The optimized two conformers of the molecule is obtained from Gaussian 09 and Gauss view program [12] and is shown in Figure 1 with calculated energies for CS point group symmetry. The molecule; TNP contains three NO2 groups along with OH. There is no energy difference between two conformers of title molecule, determined by B3LYP level 6-311++G(d,p). Possible conformers depend on the rotation of O13–H14 bond, linked to C atom. From DFT calculations with 6-311+G(d,p) basis set, the conformer 1 and 2, both are stable.
The structure optimization and zero point vibrational energy of the compound in HF and DFT(B3LYP/B3PW91) with 6-31+/6-311+G(d,p) are 77.77, 70.54, 70.09, 71.09 and 70.69 Kcal/Mol, respectively. The entire calculated values of B3LYP method are greater than the HF method. The breaking of TNP structure belongs to multiple planes which are due to the couple of three NO2 symmetrically placed about 120° in phenyl ring. The bond length between C-C of the phenyl ring is getting fractured variably. It is also evident from the bond length order as C2-C3
Vibrational assignments
In order to obtain the spectroscopic signature of the TNP compound, the computational calculations are performed for frequency analysis. The molecule, has CS point group symmetry, consists of 19 atoms, so it has 51 normal vibrational modes. On the basis of Cs symmetry, the 51 fundamental vibrations of the molecule can be distributed as 32 in-plane vibrations of A′ species and 19 out of plane vibrations of A″ species, i.e., Γvib=33 A′ + 19 A″. In the CS group symmetry of molecule is non-planar structure and has the 51 vibrational modes span in the irreducible representations.
The harmonic vibrational frequencies (unscaled and scaled) calculated at HF, B3LYP and B3PW91 levels using the triple split valence basis set along with the diffuse and polarization functions, 6-31+/6-311++G(d,p) and observed FT-IR and FT-Raman frequencies for various modes of vibrations have been presented in Tables 2 and 3. Comparison of frequencies calculated at HF and B3LYP/B3PW91 with the experimental values reveal the over estimation of the calculated vibrational modes due to the neglect of a harmonicity in real system. Inclusion of electron correlation in the density functional theory to certain extends makes the frequency values smaller in comparison with the HF frequency data. Reduction in the computed harmonic vibrations, although basis set sensitive is only marginal as observed in the DFT values using 6-311+G(d,p).
| S. No. | Observed frequency | Calculated frequency | |||||
|---|---|---|---|---|---|---|---|
| HF | B3LYP | B3PW91 | |||||
| 6-311G (d,p) | 6-31G (d,p) | 6-311G (d,p) | 6-31G (d,p) | 6-311G (d,p) | |||
| 1 | 3300 | 3972 | 3289 | 3360 | 3271 | 3325 | |
| 2 | 2960 | 3442 | 3262 | 3238 | 3264 | 3242 | |
| 3 | 2950 | 3435 | 3258 | 3234 | 3261 | 3237 | |
| 4 | 1640 | 1895 | 1699 | 1682 | 1726 | 1710 | |
| 5 | 1630 | 1878 | 1671 | 1652 | 1706 | 1686 | |
| 6 | 1620 | 1858 | 1655 | 1632 | 1693 | 1672 | |
| 7 | 1550 | 1784 | 1628 | 1613 | 1649 | 1638 | |
| 8 | 1540 | 1770 | 1611 | 1595 | 1635 | 1624 | |
| 9 | 1475 | 1678 | 1524 | 1506 | 1543 | 1528 | |
| 10 | 1450 | 1647 | 1482 | 1469 | 1493 | 1482 | |
| 11 | 1445 | 1633 | 1435 | 1420 | 1452 | 1440 | |
| 12 | 1440 | 1596 | 1399 | 1383 | 1426 | 1412 | |
| 13 | 1420 | 1572 | 1388 | 1371 | 1415 | 1401 | |
| 14 | 1340 | 1466 | 1363 | 1351 | 1379 | 1369 | |
| 15 | 1310 | 1452 | 1336 | 1319 | 1353 | 1338 | |
| 16 | 1250 | 1336 | 1317 | 1302 | 1326 | 1314 | |
| 17 | 1180 | 1312 | 1199 | 1187 | 1212 | 1202 | |
| 18 | 1150 | 1293 | 1178 | 1174 | 1172 | 1171 | |
| 19 | 1090 | 1212 | 1094 | 1091 | 1092 | 1090 | |
| 20 | 1085 | 1116 | 977 | 975 | 974 | 972 | |
| 21 | 950 | 1097 | 966 | 960 | 966 | 962 | |
| 22 | 940 | 1062 | 956 | 950 | 962 | 955 | |
| 23 | 920 | 1042 | 933 | 931 | 946 | 945 | |
| 24 | 835 | 942 | 840 | 849 | 854 | 860 | |
| 25 | 830 | 917 | 837 | 840 | 847 | 845 | |
| 26 | 800 | 893 | 830 | 809 | 841 | 833 | |
| 27 | 795 | 869 | 782 | 781 | 791 | 791 | |
| 28 | 780 | 851 | 157 | 745 | 767 | 755 | |
| 29 | 740 | 814 | 742 | 744 | 751 | 750 | |
| 30 | 730 | 803 | 741 | 728 | 746 | 739 | |
| 31 | 700 | 780 | 719 | 721 | 724 | 727 | |
| 32 | 660 | 732 | 705 | 706 | 709 | 710 | |
| 33 | 650 | 717 | 657 | 647 | 660 | 650 | |
| 34 | 550 | 599 | 549 | 548 | 550 | 550 | |
| 35 | 530 | 581 | 841 | 533 | 540 | 533 | |
| 36 | 510 | 560 | 505 | 511 | 508 | 514 | |
| 37 | 420 | 482 | 452 | 446 | 453 | 448 | |
| 38 | 400 | 439 | 404 | 402 | 406 | 403 | |
| 39 | 360 | 412 | 382 | 379 | 382 | 380 | |
| 40 | 340 | 381 | 348 | 347 | 349 | 348 | |
| 41 | 330 | 372 | 344 | 340 | 345 | 342 | |
| 42 | 320 | 357 | 326 | 321 | 327 | 323 | |
| 43 | 310 | 343 | 318 | 310 | 317 | 311 | |
| 44 | 200 | 219 | 203 | 198 | 204 | 199 | |
| 45 | 190 | 203 | 188 | 184 | 188 | 184 | |
| 46 | 150 | 171 | 155 | 1542 | 155 | 153 | |
| 47 | 120 | 137 | 128 | 124 | 128 | 125 | |
| 48 | 110 | 97 | 99 | 95 | 100 | 96 | |
| 49 | 105 | 59 | 61 | 59 | 61 | 59 | |
| 50 | 100 | 58 | 56 | 52 | 56 | 51 | |
| 51 | 90 | 54 | 45 | 50 | 45 | 50 | |
Table 3: Calculated unscaled frequencies by HF/DFT (B3LYP&B3PW91) with 6-31(d,p) and 6-311G(d,p)basis sets.
C-H vibrations: For simplicity, modes of vibrations of aromatic compounds are considered as separate ring C-H or C-C vibrations. However, as with any complex molecules, vibrational interactions occur and these labels only indicate the predominant vibration. Substituted benzenes have large number of sensitive bands, that is, bands whose position is significantly affected by the mass and electronic properties, mesomeric or inductive, of the substituents. According to the literature [21,22], in infrared spectra, most mono nuclear and poly nuclear aromatic compounds have three or four peaks in the region 3000 -3100 cm-1 [23], these are due to the stretching vibrations of the ring C-H bonds. Accordingly, in the present study, three C-H stretching vibrations are observed at 2960 and 2950 cm-1. These assigned frequencies are shifted down to the observed region which is strongly indicates that the ring vibrations affected much by the substitutions. The C-H in-plane and out-of-plane bending vibrations generally lies in the range 1000-1300 cm-1 and 950 - 800 cm-1 [24-26] respectively. Three C-H in-plane bending vibrations are identified at 1180 and 1150 cm-1and three C-H out-of-plane bending vibrations are observed at 835 and 830 cm-1. According to the literature, the in-plane and out-ofplane bending vibrational frequencies are found to be well within their characteristic regions.
CC vibrations: Generally, the C=C stretching vibrations in aromatic compounds are seen in the region of 1430-1650 cm-1 [27-29]. The C=C stretching vibrations of TNP are observed with very strong intensity at 1640, 1630 and 1620 cm-1. The stretching vibrational bands for C-C bond are observed at 1450, 1445 and 1440 cm-1. All bands lie in the lower end of the expected range when compared to the literature values. The CCC in-plane bending vibrations are observed at 740, 730 and 700 cm-1 and the out-of-plane bending vibrations are appeared at 400, 360 and 340 cm-1. These assignments are in good agreement with the literature [30,31].
NO2 vibrations: Aromatic nitro compounds have strong absorptions due to asymmetric and symmetric stretching vibrations of the NO2 group at 1570 -1485 and 1370-1320 cm-1, respectively, Hydrogen bonding has a little effect on the NO2 asymmetric stretching vibrations [32,33]. In the present case, very strong bands at 1550, 1540 and 1475 cm-1 and 1420, 1340 and 1310 cm-1 have been assigned to asymmetric and symmetric stretching modes of NO2. Each one of the stretching vibrations is moved down from the expected region. This realignment of the vibrations is purely due to the inductive effect of O of NO2 and H of Phenol. Aromatic nitro compounds have a band of weak to medium intensity in the region 590 – 500 cm-1 [34] due to the out of plane bending deformations mode of NO2 group. This is observed with strong intensity at 530, 510 and 420 cm-1 for the title compound. The in plane NO2 deformation vibrations have a week to medium absorption in the region 775-660 cm-1 [35,36]. In the present case, the NO2 deformation is found at 800, 795 and 780 cm-1. The NO2 twisting vibrations are observed at 105, 100 and 90 cm-1. One band of in plane bending pushed up and one band of out of plane bending pulled down. This is mainly due to OH.
C-N vibrations: The C-N stretching signal is raised in the region of 1350-1000 cm-1 [37]. In the present compound, the C-N stretching vibrations are observed at 1090, 1085 and950 cm-1. The C-N bending vibrations of a nitro group take place around 870 and 610 cm-1, respectively [38]. The C-N in-plane bending of a nitro group for the title compound assigned at 660, 650 and 550 cm-1, respectively. The C-N out-of-plane bending vibrations are found at 320, 310 and 200 cm-1. Some of the assigned values of C-N stretching and bending vibrations are observed at out of the expected region. The repulsion between the NO2 reduce the wavenumber of normal mode of vibrations.
C-O and O-H vibrations: The TNP compound contain a carbonyl group, the absorption caused by the C-O stretching is generally very strong [39]. Consideration of these factors lead to assign a band observed at 940 cm-1 to C-O stretching vibration. The in-plane bending and out-of-plane bending vibrations appear at 330 cm-1 and 190 cm-1 respectively. Also a weak band is observed at 110 cm-1 for C-OH twisting vibration. From the above observation, it is clear that the assigned band is in the expected region [40] and in good agreement with computed values at B3LYP/6-311+G(d,p).
The OH group gives rise to three vibrations, stretching, in-plane bending and out of plane bending vibrations. The OH group vibrations are likely to be the most sensitive to the environment, so they show pronounced shifts in the spectra of the hydrogen-bonded species. The O-H stretching vibrations are sensitive to hydrogen bonding. The O-H stretching vibration is normally observed around 3300 cm-1 [41]. Accordingly, in TNP, the O-H stretching is found at 3300 cm-1. The O-H in-plane and out-of-plane bending vibrations are usually observed in the regions 1350-1200 cm-1 and 720-590 cm-1 [42,43], respectively. The O-H in-plane and out-of-plane bending vibrations are found at 1250 cm-1 and 830 cm-1, respectively. Except one, the assignment is in line with the literature. The out of plane bending vibration is shifted up to the higher region which is may be favor of NO2.
NMR examination
NMR spectroscopy is currently used for structure elucidation of organic molecules. The combined use of experimental and computational methods offers a powerful tool to interpret and predict the structure of bulky molecules. The optimized structure of TNP is used to calculate the NMR spectra at B3LYP method with 6-311++G(d,p) level using the GIAO method and the chemical shifts of the compound are reported in ppm relative to TMS for 1H and 13C NMR spectra which are presented in Tables 4 and 5. The corresponding spectra are shown in Figure 4.
| Atom position | Solvent-DMSO | Shift (ppm) | |
|---|---|---|---|
| B3LYP/6-311+G(d,p) (ppm) | B3LYP/6-311+G(2d,p) GIAO (ppm) | ||
| C1 | 11.04 | 188.94 | 177.9 |
| C2 | 40.02 | 159.95 | 119.93 |
| C3 | 44.60 | 155.38 | 110.78 |
| C4 | 35.61 | 164.36 | 128.75 |
| C5 | 45.30 | 154.68 | 109.38 |
| C6 | 38.84 | 161.13 | 122.29 |
| N9 | 142.52 | 400.92 | 258.4 |
| N12 | 143.74 | 402.14 | 258.4 |
| N15 | 144.99 | 403.39 | 258.4 |
| O10 | 358.20 | 678.20 | 320 |
| O11 | 419.78 | 739.78 | 320 |
| O13 | 354.19 | 674.19 | 320 |
| O14 | 354.47 | 674.47 | 320 |
| O16 | 385.78 | 695.88 | 310.1 |
| O17 | 331.81 | 651.81 | 320 |
| O18 | 171.58 | 148.42 | 23.16 |
| H7 | 22.59 | 9.29 | 13.3 |
| H8 | 22.70 | 9.18 | 13.52 |
| H19 | 22.03 | 8.84 | 13.19 |
Table 4: Experimental and calculated 1H and 13C NMR chemical shift (ppm) of 2,4,6,-Nitrophenol.
| Atom position | B3LYP/6-311+G(d,p) (ppm) | TMS B3LYP/6-311+G(2d,p) GIAO (ppm) | Shift (ppm) | B3LYP/6-311+G(d,p) (ppm) | TMS B3LYP/6-311+G(2d,p) GIAO (ppm) | Shift (ppm) | B3LYP/6-311+G(d,p) (ppm) | TMS B3LYP/6-311+G(2d,p) GIAO (ppm) | Shift (ppm) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 4-Nitrophenol | 2,6-Nitrophenol | 2,4,6-Nitrophenol | ||||||||
| C1 | 8.61 | 173.84 | 165.23 | 16.23 | 166.22 | 149.99 | 8.838 | 173.62 | 164.78 | |
| C2 | 61.28 | 121.17 | 59.89 | 39.87 | 142.58 | 102.71 | 40.77 | 141.68 | 100.91 | |
| C3 | 49.78 | 132.67 | 82.89 | 43.39 | 139.06 | 95.67 | 46.62 | 135.84 | 89.22 | |
| C4 | 32.70 | 149.75 | 117.05 | 57.09 | 125.37 | 68.28 | 38.32 | 144.13 | 105.81 | |
| C5 | 50.59 | 131.87 | 81.28 | 45.32 | 137.14 | 91.82 | 47.57 | 134.89 | 87.32 | |
| C6 | 60.71 | 121.75 | 61.04 | 38.75 | 143.71 | 104.96 | 39.53 | 142.92 | 103.39 | |
| N9 | 144.60 | 403.00 | 258.4 | 140.59 | 398.99 | 258.4 | 135.74 | 394.14 | 258.40 | |
| N12 | - | - | - | 144.66 | 403.06 | 258.4 | 138.40 | 396.80 | 258.40 | |
| N15 | - | - | - | - | - | - | 141.99 | 400.39 | 258.40 | |
| O10 | 351.77 | 671.77 | 320 | 367.36 | 687.36 | 320 | 370.92 | 690.92 | 320.0 | |
| O11 | 353.39 | 673.39 | 320 | 452.81 | 772.81 | 320 | 448.08 | 768.08 | 320.0 | |
| O13 | - | - | - | 384.59 | 704.59 | 320 | 371.00 | 693.00 | 322.0 | |
| O14 | - | - | - | 336.58 | 656.58 | 320 | 374.94 | 694.93 | 319.0 | |
| O16 | - | - | - | - | - | - | 400.21 | 720.21 | 320.0 | |
| O17 | - | - | - | - | - | - | 315.40 | 635.40 | 320.0 | |
| O18(12)(15) | 196.50 | 123.49 | 73.01 | 183.18 | 136.81 | 46.37 | 156.37 | 163.62 | 7.25 | |
| H7 | 23.73 | 8.14 | 15.59 | 23.42 | 8.46 | 14.96 | 22.46 | 9.41 | 13.05 | |
| H8 | 23.87 | 8.01 | 15.86 | 23.60 | 8.28 | 15.32 | 22.85 | 9.02 | 13.83 | |
| H13 | 28.10 | 3.77 | 24.33 | - | - | - | - | - | - | |
| H14 | 25.22 | 6.65 | 18.57 | - | - | - | - | - | - | |
| H15 | 24.90 | 6.98 | 17.92 | - | - | - | - | - | - | |
| H16 | - | - | - | 23.63 | 8.25 | 15.38 | - | - | - | |
| H17 | - | - | - | 24.77 | 7.10 | 16.67 | - | - | - | |
| H19 | - | - | - | - | - | 21.12 | 10.75 | 10.37 | ||
Table 5: Experimental and calculated 1H and 13C NMR chemical shift (ppm) of 2,4,6,-Nitrophenol.
In view of the range of 13C NMR chemical shifts for similar organic molecules usually is >100 ppm [44,45], the accuracy ensures reliable interpretation of spectroscopic parameters. In the present work, 13C NMR chemical shifts in the ring are >100 ppm, as they would be expected (Table 5).
In the case of 4-Nitrophenol, the chemical shift of C1 and C4 are 165 and 117 ppm respectively. The shift is more in C1 and C4 than rest of others. This is mainly due to the substitutions of OH and NO2. The shift of H13 is 24.33 ppm which is greater than other which is purely due to O. In the case of 2,6-Nitrophenol, the chemical shift of C1, C2 and C6 are 149, 102 and 104 ppm respectively. The shift is more in C1, C2 and C6 than rest of others. This is mainly by OH and NO2.
In the case of 2,4,6-Nitrophenol, three nitro groups are added to the phenyl ring. The N atom has the most electronegative property which polarizes the electron distribution in its bond to adjacent carbon atom and thus increases the chemical shift of C1, C2, C4 and C6 (164, 100, 105 and 103 ppm respectively). The shift is more in C1, C2 and C6 than rest of others in the ring. This is also mainly due to the substitutions of OH and NO2 on C1, C2 and C6. Thus, the chemical shift of C1, C2 and C6 in the ring is increased by breaking of proton shield due to the substitutions of NO2. The shift of other C in the ring is fluctuated depending upon the positions of the NO2. The chemical shifts of all C are decreased in going from nitro to tri-nitro phenol. The chemical shift of O of phenol is decreased (73.01, 46.37 and 7.25 ppm) abruptly from nitro to tri-nitro since the isolation of O-H. This effect of isolation is the main cause to change the chemical property from nitro phenol to trinitro phenol. There is no change of chemical shift in N and O between three phenols. This view shows that the rigidity of the diamagnetic shielding of the atom. From the observation, it is clear that the change of chemical property of phenols is only in favor of NO2 groups. In addition to that, due to the accessibility of nitro groups, the phenyl ring itself is disrupted. This view is also evident that the entire property of the phenol is deflected towards nitro group.
Electronic properties-HOMO-LUMO analysis
The frontier molecular orbitals are very much useful for studying the electric and optical properties of the organic molecules. The stabilization of the bonding molecular orbital and destabilization of the antibonding can increase when the overlap of two orbitals increases. In the molecular interaction, there are the two important orbitals that interact with each other. One is the highest energy occupied molecular orbital is called HOMO represents the ability to donate an electron. The other one is the lowest energy unoccupied molecular orbital is called LUMO as an electron acceptor. These orbitals are sometimes called the frontier orbitals. The interaction between them is much stable and is called filled empty interaction.
The 3D plots of the frontier orbitals, HOMO and LUMO for TNP molecule are in gas, shown in Figures 5 and 6. According to Figure 5, the HOMO is mainly localized over three carbons of phenyl ring which connects two NO2 groups. The SP orbital lobe of O-H overlapped with SP of O of nearby NO2 group. However, LUMO is characterized by a charge distribution on carbons of phenyl ring and nitrogen of NO2 groups. When the two same sign orbitals overlap to form a molecular orbital, the electron density will occupy at the region between two nuclei. The molecular orbital resulting from in-phase interaction is defined as the bonding orbital which has lower energy than the original atomic orbital. The out of phase interaction forms the anti bonding molecular orbital with the higher energy than the initial atomic orbital. From this observation it is clear that the in and out of phase interaction are present in HOMO and LUMO respectively. The HOMO→LUMO transition implies an electron density transfer from NO2 groups. The HOMO and LUMO energy are 8.408 eV and 4.053 eV in gas phase (Figure 5). Energy difference between HOMO and LUMO orbital is called as energy gap (kubo gap) that is an important stability for structures. The DFT level calculated energy gap is 4.355 eV, show the lowering of energy gap and reflect the moderate electrical activity of the molecule.
Optical properties (HOMO-LUMO analysis)
The UV and visible spectroscopy is used to detect the presence of chromophores in the molecule and whether the compound has NLO properties or not. The calculations of the electronic structure of TNP are optimized in singlet state. The low energy electronic excited states of the molecule are calculated at the B3LYP/6-311++G (d,p) level using the TD-DFT approach on the previously optimized ground-state geometry of the molecule. The calculations are performed for 2-, 2,6-, 2,4,6-Nitrophenols with gas phase. The calculated excitation energies, oscillator strength (f) and wavelength (λ) and spectral assignments are given in Table 6. The major contributions of the transitions are designated with the aid of SWizard program [46]. TD-DFT calculations predict three transitions in the near Visible and quartz ultraviolet region for TNP molecule. In the case of 2-Nitrophenol, the strong transition is at 279.57 nm with an oscillator strength f=0.247. In the case of 2,6-Nitrophenol, strong transition is at 330.87 nm with an oscillator strength f=0.057, In the case of 2,4,6-Nitrophenol strong transition is at 418.51 nm with an oscillator strength f=0.001 assigned to an n → π* transition. This shows that, the transitions moved from quartz ultraviolet to visible region. This view indicates that, the TNP molecule colored and it is capable of having rich NLO properties. In view of calculated absorption spectra, the maximum absorption wavelength corresponds to the electronic transition from the HOMO to LUMO with maximum contribution. In this present compound, the chromophores is NO2 group, the properties are changed and enhanced from nitro phenol to tri-nitro phenol by adding NO2 group further.
| TD-DFT/B3LYP/ 6-311G++(d,p) | 2-Nitrophenol | 2,6-Nitrophenol | 2,4,6-Nitrophenol |
|---|---|---|---|
| Etotal (Hartree) | 512.10 | 534.23 | 568.59 |
| EHOMO (eV) | 7.447 | 7.809 | 8.363 |
| ELUMO (eV) | 2.683 | 3.680 | 4.296 |
| ΔEHOMO-LUMO gap (eV) | 4.763 | 4.129 | 4.067 |
| EHOMO-1 (eV) | 7.856 | 8.133 | 8.865 |
| ELUMO+1 (eV) | 1.329 | 3.001 | 3.910 |
| DEHOMO-1-LUMO+1 gap (eV) | 6.527 | 5.132 | 4.955 |
| Chemical hardness (h) | 2.381 | 2.064 | 2.033 |
| Electronegativity (c) | 2.632 | 2.985 | 3.315 |
| Chemical potential (µ) | -5.065 | -5.744 | -6.329 |
| Chemical softness(S) | 0.419 | 0.484 | 0.491 |
| Electrophilicity index (ω) | 5.387 | 7.476 | 9.851 |
| Dipole moment | 5.065 | 4.896 | 1.837 |
Table 6: Calculated energy values, chemical hardness, electro negativity, Chemical potential and Electrophilicity index of 2,4,6-Nitrophenol in Gas phase from UV-Visible.
The chemical hardness and potential, electronegativity and Electrophilicity index are calculated and their values are shown in Table 7. The chemical hardness is a good indicator of the chemical stability. The chemical hardness is decreased slightly (2.381-2.033) in going from nitro to tri nitro phenols. Hence, the present compound has much chemical stability. Similarly, the electronegativity is increased from 2.63 up to 3.315, if the value is greater than 1.7; the property of bond is changed from covalent to ionic. Accordingly, the bonds in the compound converted from covalent to ionic. Electrophilicity index is a measure of energy lowering due to maximal electron flow between donor [HOMO] and acceptor [LUMO]. From the Table 6, it is found that the Electrophilicity index of TNP is 9.851, which is too high when compared with other two molecules and this value ensure that the strong energy transformation between HOMO and LUMO. The dipole moment in a molecule is another important electronic property. Whenever the molecule has larger the dipole moment, the intermolecular interactions are very strong. The calculated dipole moment value for the title compound is 1.837 Debye. It is very low when compared to other two nitro phenols. Therefore, it is concluded that, the TNP has weak intermolecular interactions.
| 2-Nitrophenol | Gas | Assignment | Region | ||
|---|---|---|---|---|---|
| λ(nm) | E (eV) | ( f ) | Major contribution | ||
| 279.57 | 4.434 | 0.247 | L→H+1 (90%) | n→π* | Quartz UV |
| 274.66 | 4.514 | 0.012 | L→H+1 (88%) | n→π* | Quartz UV |
| 224.92 | 5.512 | 0.033 | H→L-1 (92%) | n→π* | Quartz UV |
| 2,6-Nitrophenol | |||||
| 330.87 | 3.747 | 0.057 | H→L (94%) | π→π* | Quartz UV |
| 319.78 | 3.877 | 0.016 | H→L (93%) | π→π* | Quartz UV |
| 305.49 | 4.058 | 0.007 | H→L (86%) | n→π* | Quartz UV |
| 291.39 | 4.255 | 0.004 | H→L (86%) | n→π* | Quartz UV |
| 2,4,6-Nitrophenol | |||||
| 418.51 | 2.962 | 0.001 | H→L (86%) | - | Visible |
| 374.54 | 3.310 | 0.001 | H→L (86%) | n→π* | Quartz UV |
| 370.89 | 3.342 | 0.00 | H→L (86%) | n→π* | Quartz UV |
H: HOMO; L: LUMO
Table 7: Electronic absorption spectra of 2,4,6-Nitrophenol (absorption wavelength λ(nm), excitation energies E (eV) and oscillator strengths (f)) using TD-DFT/ B3LYP/6-311++G(d,p) method gas phase.
Molecular electrostatic potential (MEP) map
The molecular electrical potential surfaces illustrate the charge distributions of molecules three dimensionally. This map allows us to visualize variably charged regions of a molecule. Knowledge of the charge distributions can be used to determine how molecules interact with one another and it is also be used to determine the nature of the chemical bond. Molecular electrostatic potential is calculated at the B3LYP/6-311+G (d,p) optimized geometry. There is a great deal of intermediary potential energy, the non red or blue regions indicate that the electro negativity difference is not very great. In a molecule with a great electro negativity difference, charge is very polarized, and there are significant differences in electron density in different regions of the molecule. This great electro negativity difference leads to regions that are almost entirely red and almost entirely blue. Greater regions of intermediary potential, yellow and green, and smaller or no regions of extreme potential, red and blue, are key indicators of a smaller electronegativity.
The color code of these maps is in the range between -0.0472 a.u. (deepest red) to 0.0472 a.u. (deepest blue) in compound. The positive (blue) regions of MEP are related to electrophilic reactivity and the negative (green) regions to nucleophilic reactivity shown in Figure 7. As can be seen from the MEP map of the title molecule, the negative regions are mainly localized on the oxygen atoms. A maximum positive region is localized on the carbon and nitrogen atoms indicating a possible site for nucleophilic attack. The MEP map shows that the negative potential sites are on electronegative atoms (O atom) as well as the positive potential sites are around the carbon and nitrogen atoms. From these results, it is clear that the carbon and nitrogen atoms indicate the strongest attraction and O atom indicates the strongest repulsion.
Polarizability and first order hyperpolarizability calculations
In order to investigate the relationships among molecular structures and non-linear optic properties (NLO), the polarizabilities and first order hyperpolarizabilities of the TNP compound was calculated using DFT-B3LYP method and 6-311+G (d,p) basis set, based on the finitefield approach.
The polarizability and hyperpolarizability tensors (αxx, αxy, αyy, αxz, αyz, αzz and βxxx, βxxy, βxyy, βyyy, βxxz, βxyz, βyyz, βxzz, βyzz, βzzz) can be obtained by a frequency job output file of Gaussian. However, α and β values of Gaussian output are in atomic units (a.u.) so they have been converted into electronic units (esu) (α1 a.u.=0.1482×10−24 esu, β; 1 a.u.=8.6393×10−33 esu). The mean polarizability (α), anisotropy of polarizability (Δα) and the average value of the first hyperpolarizability <β> can be calculated using the equations.
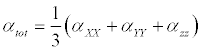 (1)
(1)
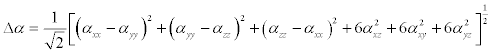 (2)
(2)
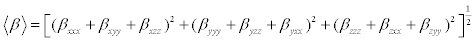 (3)
(3)
In Table 8, the calculated parameters described above and electronic dipole moment {μi (i=x, y, z) and total dipole moment } for title compound are listed. The total dipole moment is be calculated using the following equation
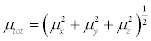 (4)
(4)
| Parameter | a.u. | Parameter | a.u. |
|---|---|---|---|
| αxx | 104.40 | βxxx | -62.31 |
| αxy | 3.88 | βxxy | -6.533 |
| αyy | 105.65 | βxyy | 22.382 |
| αxz | 1.304 | βyyy | -4.513 |
| αyz | 0.627 | βxxz | -5.928 |
| αzz | 13.88 | βxyz | 4.527 |
| αtot | 149.96 | βyyz | 5.120 |
| Δα | 288.01 | βxzz | -0.109 |
| μx | -0.903 | βyzz | -3.914 |
| µy | 1.540 | βzzz | 0.0087 |
| µz | 0.0491 | βtot | 129.66 |
| µ | 1.786 |
Table 8: The dipole moments μ (D), the Polarizability α(a.u.), the average Polarizability αo (esu), the anisotropy of the Polarizability Δα (esu), and the first hyperpolarizability β (esu) of 2,4,6-Nitrophenol.
It is well known that, molecule with high values of dipole moment, molecular polarizability, and first hyperpolarizability having more active NLO properties. The first hyperpolarizability (β) and the component of hyperpolarizability βx, βy and βz of TNP along with related properties (μ0, αtotal, and Δα) are reported in Table 8. The calculated value of dipole moment is found to be 1.837 Debye. The highest value of dipole moment is observed for component μY. In this direction, this value is equal to 1.54 D. The lowest value of the dipole moment of the TNP compound is μZ component (0.049 D). The calculated average Polarizability and anisotropy of the Polarizability is 149.96×10-24 esu and 288.01×10−24 esu, respectively. The magnitude of the molecular hyperpolarizability β, is one of important key factors in a NLO system. The B3LYP/6-311+G (d,p) calculated first hyperpolarizability value (β) is 129.66×10−30 esu. From the above results, it is observed that, the molecular Polarizability and hyperpolarizability of the title compound in all coordinates are active. So that, the TNP can be used to prepare NLO crystals and those crystal is able to produce second order harmonic waves.
Thermodynamic properties
The values of some thermodynamic parameters; thermal energy, specific heat capacity, rotational constants and entropy calculated by B3LYP with 6-311+G(d,p) method at 298.15 K and 1.00 Atm pressure are listed in the Table 9. The variation of thermo dynamical parameters seems to be important because the entire chemical, electrical and thermal properties of the compound depend upon these factors. The specific heat capacity of the TNP is 85.18 cal/mol/K, which is greater than other two phenols. When the number of NO2 is added, the specific heat capacity of the phenols is increased. Therefore, TNP in crystal form has electrical property and can be used for many industrial applications. Similarly, the values of thermal energy and entropy of TNP is higher than rest of other. From this observation, it is inferred that, the TNP has good chemical reactivity according to the second law of thermodynamics in thermo chemical field.
| Compound | 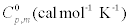 |
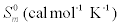 |
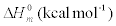 |
|---|---|---|---|
| 2-Nitrophenol | 27.86 | 83.32 | 4.712 |
| 2,4-Nitrophenol | 35.65 | 78.73 | 5.236 |
| 2,4,6-Nitrophenol | 43.25 | 85.18 | 5.549 |
Table 9: Thermodynamic properties at different temperatures on the B3LYP/6- 311+G(d,p) level for Nitrophenols.
In the present investigation, FT-IR and FT-Raman spectra of the 2,4,6-Nitrphenol were recorded and the observed vibrational frequencies were assigned depending upon their expected region. The hybrid computational calculations were carried out by HF and DFT (B3LYP and B3PW91) methods with 6-31+G(d,p) and 6-311++G(d,p) basis sets and the corresponding results were tabulated. The alternation of structure and some of the parameters of nitro phenol due to the subsequent substitutions of NO2 was investigated. The vibrational sequence pattern of the molecule related to the substitutions was analyzed. Moreover, 13C NMR and 1H NMR were calculated by using the gauge independent atomic orbital (GIAO) method with B3LYP methods and the 6-311++G(d,p) basis set and their spectra were simulated and the chemical shifts related to TMS were compared. A study on the electronic properties; absorption wavelengths, excitation energy, dipole moment and frontier molecular orbital energies, were performed by HF and DFT methods. The calculated HOMO and LUMO energies and the kubo gap analysis show that the occurring of charge transformation within the molecule. Besides frontier molecular orbitals (FMO), molecular electrostatic potential (MEP) was performed. NLO properties related to Polarizability and hyperpolarizability was also discussed. The thermodynamic properties (thermal energy, heat capacity and entropy) of the title compound are calculated in gas phase and were interpreted with different types of phenols.