Journal of Thermodynamics & Catalysis
Open Access
ISSN: 2157-7544
ISSN: 2157-7544
Research Article - (2016) Volume 7, Issue 2
In the present paper, in situ ring opening anionic polymerization of laurolactam towards polyamide 12 (PA12) was investigated, during reactive melt blending. The reaction was taken place in an internal mixer, in the presence of sodium caprolactam (catalyst), and toluene diisocyanate (activator). The effect of catalyst and activator contents on initiation time of the reaction and the residual monomer was carried out in this study. Solvent extraction method was used in order to remove the residual monomer. The experimentation is further undergone to statistical analysis to extract the absolute optimal values of activator- catalyst content in synthesized polyamide 12. Two-factor design in Response Surface Method (RMS) is suitably applied for validation analysis of experimental data. The optimum content of catalyst and activator was obtained 2.53% and 1.15%, which offers the polyamide 12 with minimum residual monomer equal to 1.26%.
Keywords: Ring opening anionic polymerization; Polyamide12; Laurolactam; Sodium caprolactam; Toluene diisocyanate
Polyamides are well-known engineering thermoplastic materials which have high mechanical strength, high melting point, low density and high potential of forming complicated structures from molding injection [1]. They widely used in industrial applications for their remarkable mechanical and thermal properties [2-5].
Polyamides are prepared by applying three technique [6], Hydrolytic [7], Solid-phase [6] and Anionic polymerization. PA12 can be obtained through anionic polymerization of laurolactam. This method must be carried out strictly in the absence of water [8].
The presence of an anionically activated monomer and an activator is essential for starting the anionic polymerization. Only the correct ratios of monomer, activator, and catalyst will complete the reaction so that it will give the least residual monomer [8,9]. The initiators of anionic lactam polymerization are the lactamate anions being formed by the reaction of a lactam with a strong base [10]. Schwartz and Paul proposed the use of the alkaline and earth alkaline metals, especially sodium and potassium, and their oxides, hydroxides, hydrides, carbonates, and other reactive compounds of these metals, including organometallic reagents as catalyst [10].
Luisierv et al. worked on improving impregnation prior to in-situ polymerization of Polyamide 12 by exploiting a very low monomer viscosity. The polymerization kinetics of anionic PA12 was studied and the viscosity changes during polymerization were measured to determine how the processing temperature influences the impregnation time [11]. Also there are some researches on investigation the effect of catalyst- activator content in the formulation.
Ahmadi et al. investigated the effect of catalyst and activator on the residual monomer and other characteristics of PA6. The experimental results showed that the addition of 3% catalyst and 3% activator to the formulation gave the best properties. These conditions led to the lowest residual monomer and better mechanical properties as well [12].
Experimental Design and Response Surface Methodology (RSM) has been used for a long time to develop descriptive–predictive models to fulfill optimization purposes in different areas of dosage form design [13-15]. Its popularity stems from its ability to locate the combination of formulation and/or manufacturing parameter values that are most likely to produce the desired release profile.
In this study anionic polymerization of Laurolactam was studied to produce polyamide 12, and then analytical tests were applied to investigate the effect of sodium caprolactam (NaCL), as catalyst and toluene diisocyanate (TDI) as an activator, on reaction time and the residual monomer, in different concentrations. Moreover an optimization study and statistical analysis of these properties was also carried out using Design Expert Software. The optimization study was evaluated in order to validate the experimental results and to identify the best-fit values.
Materials and methods
The monomer used in this project was laurolactam supplied by Evonik Co., Germany. Toluene diisocyanate (TDI), used as an activator, was obtained from Karoon Co., Iran. The catalyst, sodium Caprolactam was obtained from Karangin Co.
Polymerization of laurolactam was carried out in a 50 mL chamber of a Haake type internal mixer model Sys 9000 for the sample preparation and the subsequent evaluations. The rotor speed was fixed at 60 rpm. The temperature was set at 180°C under the nitrogen atmosphere. By changing the catalyst and activator concentration at three levels (1, 2 and 3%), nine different formulations where synthesized which were named as I1C1, I1C2, I1C3, I2C1, I2C2, I2C3, I3C1, I3C2 and I3C3 respectively. in these formulations “I” refers to initiators (activator) and “C” refers to catalyst. also subscripts 1, 2 and 3 refers to the concentration percentage of each material.
Residual monomer characterization
Different methods have been proposed to determine the conversion of monomers to polymer. Among these methods the gravimetric method was applied here. This was based on the mass ratio of polymerized products of which the residual monomers were removed by solvent extraction. Toluene was used as a solvent for Soxhlet extraction of un-reacted laurolactam. Monomer extraction was continued for 40 h at 120°C. Then, the samples were dried in a vacuum oven for 30 h at 70°C.
In order to confirm the monomer extraction results, TGA was performed for detecting and also determining the residual monomer content of the PA12 samples. TGA tests were conducted under nitrogen flow from 25°C up to 600°C and then continued up to 1000°C under oxygen. The heating rate was 10°C/min.
Statistical analysis
The Statistically designed experiments play an important role in Science, Engineering, and Industry. The experimentation is a part of scientific method, which requires observing and gathering the information about how the process and system works. In an experiment, some inputs transform into an output that have one or more observable response variables. Therefore, useful results and conclusions can be drawn by experiment. Experimenter needs to plan and design the experiment, and analyze the results, in order to obtain an objective conclusion. There are many types of experiments used in real-world situations and problems. Statistical analysis (regression and ANOVA analysis) of the responses are carried out to estimate the coefficients of the polynomial equation of the response by regression and to check the significance of the regression coefficients of independent variables and interaction variables by ANOVA. Analysis of Variance (ANOVA) table is used to determine the significance of the different degrees, and cross-product terms of the polynomial.
The present study is conducted to find the optimum catalyst and activator contents validate the obtained experiment results; Response Surface Methodology (RSM) is adopted to determine the functional relationships between the process variables and initiation reaction time and also residual monomer. In this case, non-linear trends in the response are likely and hence a second order polynomial model could be considered to fit adequately the experimental results. Here there were only two factors (catalyst and activator %) to be analyzed.
Synthesis of polymer
The Figure 1 shows the torque versus mixing time for different formulations. In all cases, the torque started to increase at a time, which is called reaction time. Duration time differed, depending on the formulation. Due to the lower activation energy required for the nucleophilic attack of the anionic caprolactam to its activated lactam group, after the addition of only 1% of TDI, the polymerization took place. For all samples except samples I1C3 and I3C1, the torque curves increased very rapidly after about 50-70 seconds of mixing, indicating the starting point of the polymerization. Diagrams reached to its maximum after about 120 seconds and then decreased, which indicated the end of polymerization [16].
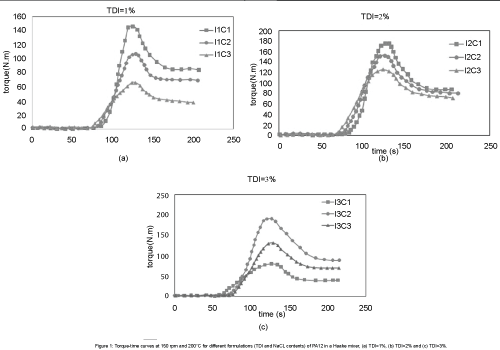
Figure 1: Torque-time curves at 150 rpm and 200°C for different formulations (TDI and NaCL contents) of PA12 in a Haake mixer, (a) TDI=1%, (b) TDI=2% and (c) TDI=3%.
Catalyst and activator content had a considerable effect on polymerization. Catalyst led the reaction to be occurred faster and activator increased the anionic attack speed. The outcome of these two factors together is shown in Figure 2. It is obvious from Figure 2, polymerization reaction time decreased, by increasing the amount of catalyst (NaCL) and the activator (TDI), but the effect of NaCL is more significant. Although lower reaction time seemed to be better but it may limit the polymerization and reduce the molecular weight too.
Characterization of the synthesized polymers
Residual monomer determination: Monomer conversion is an important parameter, because a little content of monomer sometimes can remarkably influence the properties of specimen. Generally, the loss weight of sample from 200°C up to 320°C was corresponding to Laurolactam content [17]. The Figure 3 shows the effect of catalyst and activator concentration on the residual monomer content of the samples. This figure clearly shows that in all of the concentrations of the activator, by increasing the amount of catalyst, residual monomer percentage decreased, while activator had an inverse effect.
The maximum conversion of Laurolactam was reported to be around 97.3% and 96% (2.7%-4%residual monomer) by Libo Du et al. and Ha and White respectively [18]. However, the residual monomer content (Figure 3) in this work was reduced to 1.86% for PA12 containing 1% catalyst and 1% activator; which was lower than the cited references. The improvement in the polymerization efficiency is believed to be caused by the use of a double functional cyanate (TDI). Because in this case the reaction proceeded from two sides of the activator, and the monomers were consumed more rapidly. The results of TGA confirmed the Soxhlet results and both of them showed the same procedure as it is shown in Table 1.
| Sample | TDI | NaCl | T(peak1) | T(peak2) | T(10%wt) | T(30%wt) | T(50%wt) | Residual monomer (TGA)% | Residual monomer (Soxhlet)% |
|---|---|---|---|---|---|---|---|---|---|
| I1C1 | 1 | 1 | 467.25 | 357.27 | 373.562 | 449.776 | 459.946 | 3.6 | 3.6 |
| I1C2 | 1 | 2 | 458.8 | 359.27 | 377.128 | 446.616 | 457.883 | 1.9 | 1.8 |
| I1C3 | 1 | 3 | 462.55 | 359.3 | 384.768 | 449.402 | 453.926 | 1.8 | 1.8 |
| I2C1 | 2 | 1 | 464.026 | 238.96 | 241.585 | 429.848 | 452.685 | 12.2 | 11.9 |
| I2C2 | 2 | 2 | 465.092 | 348.3 | 360.211 | 443.515 | 455.865 | 2.7 | 2.7 |
| I2C3 | 2 | 3 | 463.12 | 348.31 | 355.331 | 441.107 | 455.865 | 2.2 | 2.3 |
| I3C1 | 3 | 1 | 460.94 | 244.56 | 213.101 | 251.874 | 426.57 | 33.5 | 33.5 |
| I3C2 | 3 | 2 | 464.29 | 338.34 | 343.933 | 441.083 | 454.782 | 3.8 | 3.7 |
| I3C3 | 3 | 3 | 464.27 | 343.404 | 342.708 | 438.934 | 453.792 | 3.4 | 3.5 |
Table 1: TGA and Soxhlet results of residual monomer for different formulations.
Statistical analysis of experimental results: Second-order polynomial equation was developed using RSM including quadratic terms and two-factor interactions that explained the nonlinear nature of the response [19]. The second-order polynomial equations are expressed generally in the following form:
γ=a0+a1X1+a2X2+a3X1X2+a4X12+a5X22+E (1)
Where a1–a5 are the coefficients of the respective variables and their interaction terms, and E is an error term. Results of analysis are usually considered significantly if their corresponding P values are less than 0.05. A two-factor, multiple-level full factorial design was used to construct the response surface and the polynomial model for the polyamide12 polymerization, optimization. The catalyst (NaCL) (X1) and also the activator percentage (X2) were studied at three levels: 1, 2 and 3%.
In this study, the effect of catalyst and activator on the residual monomer and reaction time of the synthesized polyamide 12 was investigated using two-factor design which is one of the response surface methodology designs. The results were analyzed by using Design Expert Software Version 8 to establish the mathematical functional relations as well as a number of statistics to confirm the variables of the models.
Analysis of the reaction time
The results of the ANOVA, two-factor design experiments on the effect of the process variable over the reaction time are tabulated in Tables 2 and 3. A suitable model was selected from these results. Through the estimation of all regression coefficients, the experimental response could be modeled as a polynomial equation that showed the effect of process variable (activator and catalyst content) on the reaction time of the synthesized polyamide 12. The quadratic function obtained is given in Equation (2). This equation was used to generate the predicted values using the software as shown in Table 4. A graph is plotted between the predicted and experimental (actual) values as shown in Figure 4. Here the transform function was chosen as (y’=(y+k)3).
| Source | Sum of squares | df | MeanSquare | F - value | P- value Prob>F |
|---|---|---|---|---|---|
| Model | 6.063E+010 | 4 | 1.516E+010 | 10.81 | 0.0026 |
| A-catalyst | 1.057E+010 | 1 | 1.057E+010 | 7.54 | 0.0252 |
| B-activator | 3.084E+010 | 1 | 3.084E+010 | 21.99 | 0.0016 |
| AB | 1.396E+010 | 1 | 1.396E+010 | 9.96 | 0.0135 |
| B2 | 5.262E+009 | 1 | 5.262E+009 | 3.75 | 0.0887 |
| Residual | 1.122E+010 | 8 | 1.402E+009 | ||
| Total | 7.185E+010 | 12 |
Table 2: Analysis of variance (ANOVA) results for reaction time of PA12 polymerization.
| Std.Dev | 37446.20 | R-Squared | 0.8439 |
| Mean | 3.623E+005 | Adj R-Squared | 0.7658 |
| C.V.% | 10.34 | Pred R-Squared | -0.0553 |
| PRESS | 7.582E+010 | Adeq R-Squared | 11.262 |
Table 3: Modeling parameters for raction time of PA12 polymerization.
| Sample | Reaction time(ACTUAL), (s) | (Reaction time)^3 (ACTUAL), (s) | (Reaction time)^3 (PREDICTED), (s) |
|---|---|---|---|
| I1C1 | 78.839 | 490030.7361 | 513300 |
| I1C2 | 74.754 | 417737.3512 | 412300 |
| I1C3 | 69.0359 | 329022.0265 | 311200 |
| I2C1 | 77.149 | 459188.3947 | 422900 |
| I2C2 | 72.612 | 382846.9547 | 380900 |
| I2C3 | 66.424 | 293072.5039 | 339000 |
| I3C1 | 58.43 | 199483.8121 | 251800 |
| I3C2 | 69.268 | 332351.7308 | 268900 |
| I3C3 | 65.014 | 274802.4882 | 286000 |
Table 4: Predicted Vs Actual values of reaction time.
The Model F-value of 10.81 implied the significancy of model. There was only a 0.26% chance that a "Model F-Value" this large could occur due to noise.
Values of "Prob>F" less than 0.0500 indicate model terms are significant. In this case A, B, AB were significant model terms. Values greater than 0.1000 indicate the model terms are not significant. If there are many insignificant model terms (not counting those required to support hierarchy), model reduction may improve the model. Thus the effect of activator, catalyst and the cross product of activator and catalyst were more prominent (Figures 5 and 6).
A negative "Pred R-Squared" implied that the overall mean was a better predictor of present response than the current model. "Adeq Precision" measured the signal to noise ratio. A ratio greater than 4 is desirable. Here the ratio of 11.262 indicated an adequate signal. This model can be used to navigate the design space.
Final equation in terms of coded factors: (reaction time)3=+3.809E+005-41967.65 × A-71692.01 × B+59081.85 × A × B-40356.60 × B2 (2)
An interaction occurs when the response is different depending on the settings of two factors. Plots in Figure 7 make it easy to interpret two factor interactions. They will appear with two non-parallel lines, indicating that the effect of one factor depends on the level of the other.
Analysis of the residual monomer
The results of the ANOVA, two-factor design experiments on the effect of the process variable over residual monomer are tabulated in Table 5, part (a). Through the estimation of all regression coefficients, the experimental response was modeled as a polynomial equation which showed the effect of process variable on the residual monomer of synthesized polyamide 12. The quadratic function obtained is given in Equation (4). This equation was used to generate the predicted values using the software as shown in Table 6. A graph is plotted between the predicted and experimental (actual) values as shown in Figures 8-11.
| (a). Linear trasnform function | |||||
|---|---|---|---|---|---|
| Source | Sum of squares | Df | Mean Square | F - value | P- value Prob>F |
| Model | 830.82 | 5 | 166.16 | 14.05 | 0.0016 |
| A-catalyst | 290.50 | 1 | 290.50 | 24.56 | 0.0016 |
| B-activator | 185.72 | 1 | 185.72 | 15.70 | 0.0054 |
| AB | 200.34 | 1 | 200.34 | 16.94 | 0.0045 |
| A2 | 102.20 | 1 | 102.20 | 8.64 | 0.0217 |
| B2 | 7.95 | 1 | 7.95 | 0.67 | 0.4393 |
| Residual | 82.79 | 7 | 11.83 | ||
| Total | 913.62 | 12 | |||
| (b) Transform function=(y+k)-1 | |||||
| Source | Sum of Squares | df | Mean Square | F - value | P- value Prob>F |
| Model | 0.26 | 5 | 0.051 | 106.35 | <0.0001 |
| A-catalyst | 0.13 | 1 | 0.13 | 266.99 | <0.0001 |
| B-activator | 0.095 | 1 | 0.095 | 196.45 | <0.0001 |
| AB | 6.92×10-9 | 1 | 6.92×10-9 | 1.43×10-5 | 0.9971 |
| A2 | 0.032 | 1 | 0.032 | 66.01 | <0.0001 |
| B2 | 1.378×10-3 | 1 | 1.378×10-3 | 2.66 | 0.1347 |
| Residual | 3.374×10-3 | 7 | 4.820×10-4 | ||
| total | 0.26 | 12 | |||
Table 5: Analysis of variance (ANOVA) results for the residual monomer, (a) Linear trasnform function and (b) Transform function=(y+k)-1.
The Model F-value of 14.05 implied the significancy of the model. There was only a 0.16% chance that a "Model F-Value" this large could occur due to noise. Due to "Prob>F" values which were less than 0.0500 model terms were significant. In this case A, B, AB, A2 were significant model terms.
The "Pred R-Squared" of 0.1033 is not as close to the "Adj R-Squared" of 0.8447 as is normally expected. This may indicate a large block effect or a possible problem with the model and/or data. Here the ratio of 13.373 for "Adeq Precision" indicated an adequate signal.
Final equation in terms of coded factors: The residual monomer=+2.27-6.96 × A+5.56 × B-7.08 × A × B+6.08 × A2+1.70 × B2 (4)
Final equation in terms of actual factors: The residual monomer=+ 7.87140-17.13644 × catalyst+12.93044 × activator-7.07703 × catalyst × activator+6.08306 × catalyst2+1.69681 × activator2 (5)
As it is clear from Table 6, this model did not present appropriate prediction for the residual monomer, therfore the transform function was chosen to be (y+k)-1 and again the quadradic model was applied. The results of the new model is presented in Table 5 (part b). In this case A, B, A2 were significant model terms.
| Sample | Residual monomer(actual), (%) | Residual monomer(predicted by Linear trasnform function), (%) | Residual monomer(predicted by (y+k)-1 trasnform function), (%) |
|---|---|---|---|
| I1C1 | 3.6 | 4.3 | 3.8 |
| I1C2 | 1.9 | -1.5 | 1.9 |
| I1C3 | 1.9 | 4.6 | 1.8 |
| I2C1 | 12.2 | 15.1 | 8.7 |
| I2C2 | 2.7 | 2.2 | 2.7 |
| I2C3 | 2.2 | 1.4 | 2.4 |
| I3C1 | 33.5 | 29.6 | 83.3 |
| I3C2 | 3.8 | 9.5 | 3.6 |
| I3C3 | 3.4 | 1.6 | 3.3 |
Table 6: Predicted residual monomer vs the actual values.
Final equation in terms of coded factors: (residual monomer)-1=+0.37+0.15 × A-0.13 × B+4.160E-005 × A × B-0.11× A2+0.022 × B2 (6)
Final equation in terms of actual factors: (residual monomer)-1=-0.012639+0.57570 × catalyst-0.21507 × activator+4.16047E-005 × catalyst × activator-0.10733 × catalyst2+0.022340 × activator2 (7)
Since the variation in catalyst and activator content between the experimental value and predicted value was not that large, and the desirability factor was 82%, the data obtained from the experiment can be considered as the best-fit value, as it is shown in Tables 6-8. The validation checks using response surface method (two-factor design), gave 1.15% activator and 2.53% catalyst as the optimum values for the minimum residual monomer. This formulation led to the monomer content equal to 1.26%. Therefore by investigating a set of random formulations and applying statistical analysis, a prediction of optimum condition was simply done. According to this prediction, a large number of possible formulations, which should be synthesized in order to determine the best catalyst and activator content, would be omitted.
| Name | Goal | Lower Limit | Higher Limit |
|---|---|---|---|
| catalyst | is in range | 1 | 3 |
| activator | is in range | 1 | 3 |
| (reaction time)^3 | is in range | 199484 | 490031 |
| (residual monomer)^-1 | maximize | 0.0298531 | 0.537634 |
Table 7: Objectives of combined effect – reaction time and residual monomer.
| Catalyst% | Activator % | (reaction time)^3 | (residual monomer)^-1 | Desirability |
|---|---|---|---|---|
| 2.53 | 1.15 | 374738.106 | 0.79 | 1.000 |
Table 8: Final Result for combined effect - reaction time and residual monomer.
In this study, the effect of catalyst and activator on reaction time and residual monomer during the ring opening polymerization of polyamide 12 was investigated. The experimental results are validated using Response Surface Method (RMS). The following facts are concluded from the present research:
• The response surface method along with ANOVA technique is found to be an effective approach for optimization of decreasing the residual monomer of synthesized PA12.
• Evidently, activator and the cross product of activator and catalyst are detected to be the significant factors which effects on reaction time.
• According to the above results, it can be concluded that the catalyst (2.53%) and activator (1.15%) is the optimal combination for achieving the required objectives (the least residual monomer content).