This century has been told to be the century of complexity [1]. Nowadays the question “what is complexity?” is circulating over the scientific crossroads of physics, biology, mathematics and computer science, although under the present understanding of the world could be no urgent to answer this question. However, many different points of view have been developed to this respect and hence a lot of different answers can be found in the literature. Here we explain in detail one of these options. On the most basic grounds, an object, a procedure, or system is said to be “complex” when it does not match patterns regarded as simple. This sounds rather like an oxymoron but common knowledge tells us what is simple and complex: simplified systems or idealizations are always a starting point to solve scientific problems. The notion of “complexity” in physics [2,3] starts by considering the perfect crystal and the isolated ideal gas as examples of simple models and therefore as systems with zero “complexity”. Let us briefly recall their main characteristics with “order”, “information” and “equilibrium”. A perfect crystal is completely ordered and the atoms are arranged following stringent rules of symmetry. The probability distribution for the states accessible to the perfect crystal is centered on a prevailing state of perfect symmetry. A small piece of “information” is enough to describe the perfect crystal: the distances and the symmetries that define the elementary cell. The “information” stored in this system can be considered minimal. On the other hand, the isolated ideal gas is completely disordered. The system can be found in any of its accessible states with the same probability. All of them contribute in equal measure to the “information” stored in the ideal gas. It has therefore maximum “information”. These two simple systems are extrema in the scale of “order” and “information”. It follows that the definition of “complexity” must not be made in terms of just “order” or “information”. It might seem reasonable to propose a measure of “complexity” by adopting some kind of distance from the equiprobable distribution of the accessible states of the system. Defined in this way, “disequilibrium” would give an idea of the probabilistic hierarchy of the system. “Disequilibrium” would be different from zero if there are privileged, or more probable, states among those accessible. But this would not work. Going back to the two examples we began with, it is readily seen that a perfect crystal is far from an equidistribution among the accessible states because one of them is totally prevailing, and so “disequilibrium” would be maximum. For the ideal gas, “disequilibrium” would be zero by construction. Therefore such a distance or “disequilibrium” (a measure of a probabilistic hierarchy) cannot be directly associated with “complexity”. In Figure 1.1 we sketch an intuitive qualitative behavior for “information” H and “disequilibrium” D for systems ranging from the perfect crystal to the ideal gas. This graph suggests that the product of these two quantities could be used as a measure of “complexity”: C=H · D. The function C has indeed the features and asymptotical properties that one would expect intuitively: it vanishes for the perfect crystal and for the isolated ideal gas, and it is different from zero for the rest of the systems of particles. We will follow these guidelines to establish a quantitative measure of “complexity”. Before attempting any further progress, however, we must recall that “complexity” cannot be measured univocally, because it depends on the nature of the description (which always involves a reductionist process) and on the scale of observation. Let us take an example to illustrate this point. A computer chip can look very different at different scales. It is an entangled array of electronic elements at microscopic scale but only an ordered set of pins attached to a black box at a macroscopic scale. We shall now discuss a measure of “complexity” based on the statistical description of systems. Let us assume that the system has N accessible states {x1, x2,..., xN } when observed at a given scale. We will call this an N-system. Our understanding of the behavior of this system determines the corresponding probabilities {p1, p2 , ..., pN } (With the condition 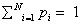) of each state (pi>0 for all i). Then the knowledge of the underlying physical laws at this scale is incorporated into a probability distribution for the accessible states. It is possible to find a quantity measuring the amount of “information”. Under to the most elementary conditions of consistency, Shannon [4] determined the unique function H ( p1 , p2 , ..., pN ) that accounts for the “information” stored in a system:

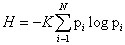(1.1)

Figure 1.1: Sketch of the intuitive notion of the magnitudes of “information” (H) and “disequilibrium” (D) for the physical systems and the behavior intuitively required for the magnitude “complexity”. The quantity C = H · D is proposed to measure such a magnitude.

Where K is a positive constant. The quantity H is called information. The redefinition of information H as some type of monotone function of the Shannon entropy can be also useful in many contexts as we shall show in the next sections. In the case of a crystal, a state xc would be the most probable pc∼1, and all others xi would be very improbable, pi~0 i ≠ c. Then Hc∼0. On the other side, equiprobability characterizes an isolated ideal gas, pi~1/N so Hg~K log N, i.e., the maximum of information for a N-system. (Notice that if one assumes equiprobability and K=κ ≡ Boltzmann constant , H is identified with the thermodynamic entropy, S=κ log N). Any other N-system will have an amount of information between those two extrema. Let us propose a definition of disequilibrium D in a N-system [5]. The intuitive notion suggests that some kind of distance from an equiprobable distribution should be adopted. Two requirements are imposed on the magnitude of D: D>0 in order to have a positive measure of “complexity” and D=0 on the limit of equiprobability. The straightforward solution is to add the quadratic distances of each state to the equiprobability as follows:

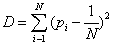(1.2)

According to this definition, a crystal has maximum disequilibrium (for the dominant state, pc~1, and Dc → 1 for N → ∞) while the disequilibrium for an ideal gas vanishes (Dg~0) by construction. For any other system D will have a value between these two extrema. We now introduce the definition of complexity C of a N-system [6,7]. This is simply the interplay between the information stored in the system and its disequilibrium:

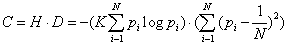(1.3)

This definition fits the intuitive arguments. For a crystal, disequilibrium is large but the information stored is vanishingly small, so C~0. On the other hand, H is large for an ideal gas, but D is small, so C~0 as well. Any other system will have an intermediate behavior and therefore C>0. As was intuitively suggested, the definition of complexity (Equation: 1.3) also depends on the scale. At each scale of observation a new set of accessible states appears with its corresponding probability distribution so that complexity changes. Physical laws at each level of observation allow us to infer the probability distribution of the new set of accessible states, and therefore different values for H, D and C will be obtained. The straight forward passage to the case of a continuum number of states, x, can be easily inferred. Thus we must treat with probability distributions with a continuum support, p(x), and normalization condition 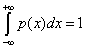Disequilibrium has the limit 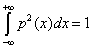and the complexity could be defined by:

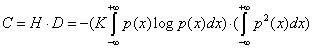(1.4)

As we shall see, other possibilities for the continuous extension of C are also possible. Direct simulations of the definition give the values of C for general N-systems. The set of all the possible distributions { p1, p2 , ..., pN } where an N-system could be found is sampled. For the sake of simplicity H is normalized to the interval [0, 1]. Thus 1 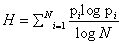For each distribution {pi} the normalized information H ({pi}), and the disequilibrium D ({pi}) Equation: 1.2 are calculated. In each case the normalized complexity C=H · D is obtained and the pair (H, C) stored. These two magnitudes are plotted on a diagram (H,C(H )) in order to verify the qualitative behavior predicted in Figure 1.1. The relationship between H and C is not univocal. Many different distributions {pi} store the same information H but have different complexity C. Figure 1.2 displays such a behavior for N=3. If we take the maximum complexity Cmax (H ) associated with each H a convex curve with a maximum is found. Every 3-system will have a complexity below this line and upper the line of Cmin (H ) and also upper the minimum envelope complexity Cminenv . In Figure 1.3 curves Cmax (H ) for the cases N=3, . . . , 10 are also shown. Let us observe the shift of the complexity curve peak to smaller values of entropy for rising N. This fact agrees with the intuition telling us that the biggest complexity (number of possibilities of ‘complexification’) be reached for lesser entropies for the systems with bigger number of states. Let us return to the point at which we started this discussion. Any notion of complexity in physics [2, 3] should only be made on the basis of a well-defined or operational magnitude [6, 7]. But two additional requirements are needed in order to obtain a good definition of complexity in physics: (1) the new magnitude must be measurable in many different physical systems and (2) a comparative relationship and a physical interpretation between any two measurements should be possible. Many different definitions of complexity have been proposed to date, mainly in the realm of physical and computational sciences. Among these, several can be cited: algorithmic complexity (Kolmogorov-Chaitin) [8,9], the Lempel-Ziv complexity [10], the logical depth of Bennett [11], the effective measure complexity of Grassberger [12], the complexity of a system based in its diversity [13], the thermodynamical depth [14], the ε-machine complexity [15] , the physical complexity of genomes [16], complexities of formal grammars, etc. The discussion on what can be learned or what prediction can be checked in an experiment or what new physics can be derived from the study of this type of measures has always been a controverted discussion [17-20]. This forms part of the evolution of ideas and nobody knows what can be found at the end of the path if it is not walked. This is just the object of science and, for this concrete case, Hawking claimed at the end of the past twentieth century: “I think the next century will be the century of complexity” [1]. The definition of complexity Equation:1.3 proposed in this section offers a point of view based on a statistical description of systems at a given scale. In this scheme, the knowledge of the physical laws governing the dynamic evolution in that scale is used to find its accessible states and its probability distribution. This process would immediately indicate the value of complexity. In essence this is nothing but interplay between the information stored by the system and the distance from equipartition (measure of a probabilistic hierarchy between the observed parts) of the probability distribution of its accessible states. Besides giving the main features of an “intuitive” notion of complexity, we will show in this chapter that we can go one step further and to compute this quantity in other relevant physical situations and in continuum systems. The most important point is that the new definition successfully enables us to discern situations regarded as complex. For example, we have performed different applications in complex systems with some type of discretization: one of them was the study of this magnitude in a phase transition in a coupled map lattice [21] and the other one was its calculation for the time evolution of a discrete gas out of equilibrium [22]. Other applications to more realistic systems can also be found in the literature, see for instance this major reference which is the only monograph published on the topic of statistical complexity applied to electronic systems [23]. In this monograph, different information measures applied to the description of electronic properties are addressed. One of them, the Fisher-Shannon information [24], presents a parallelism with the statistical complexity here presented. Both of them are based on the product of two information measures that give complementary descriptions of the concentration and uncertainty of the probability density. Thus, Shannon and Fisher information’s can be seen as global and local measures of the spreading or delocalization of the electronic cloud, respectively, and they can also be useful to show the electron correlation phenomenon [25]. In the next section, we are concerned with showing some applications of this type of statistical indicators in many electron systems such as atoms, molecules and clusters. Before that, we present the formulas that will be used in all our calculations.

Figure 1.2: In general, dependence of complexity (C) on normalized information (H) is not univocal: many distributions {p_i} can present the same value of H but different C. This is shown in the case N = 3.

Figure 1.3: Complexity (C = H ·D) as a function of the normalized information (H) for a system with two accessible states (N = 2). Also curves of maximum complexity (C_max) are shown for the cases: N = 3;:::; 10.

A similar statistical indicator to the statistical complexity C that has also been applied in several contexts is the Fisher-Shannon entropy, P. This entropic product measure [24] is also defined as the product of two magnitudes, in this case the exponential Shannon entropy, J, and the Fisher information, I. Now, we summarize the formulas and the nomenclature that we will use in all the next section for both indicators, C and P.

The measure of complexity C has been defined as

C=H · D (1.5)

Where H represents the information content of the system and D gives an idea of how much concentrated is its spatial distribution. We will use the simple exponential Shannon entropy [26-28], in the position and momentum spaces, as a measure of H. It takes the form, respectively,

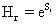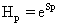, (1.6)

Where Sr and Sp are the Shannon information entropies [29],

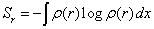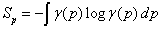, (1.7)

and ρ(r) and γ(p) are the densities normalized to 1 of the quantum system in position and momentum spaces, respectively.

The disequilibrium is:

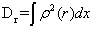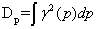, (1.8)

In this manner, the final expressions for C in position and momentum spaces are:

C_r = H_r ·D_r ,C_p = H_p ·D_p (1.9)

Let us remark at this point the coincidence of the indicator logCr with the quantity structural entropy, Sstr, introduced by Varga and Pipek as a meaningful parameter to characterize the shape of a distribution [30-32].

Second, the Fisher-Shannon information [24], P, in the position and momentum spaces, is given respectively by

P_r= J_r · I_r ,P_p = J_p ·I_p (1.10)

Where the first factor

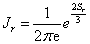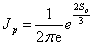, (1.11)

is a version of the exponential Shannon entropy, and the second factor

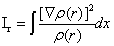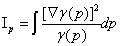, (1.12)

is the Fisher information measure [33], that quantifies the narrowness of the probability density.

Different applications of both magnitudes, the statistical complexity and the Fisher- Shannon entropy, in electronic systems are collected in this section.

The H -atom

The atom can be considered a complex system. Its structure is determined through the well-established equations of Quantum Mechanics [34,35]. Depending on the set of quantum numbers defining the state of the atom, different conformations are available to it. As a consequence, if the wave function of the atomic state is known, the probability densities in the position and the momentum spaces are obtained, and from them, the different statistical magnitudes such as Shannon and Fisher informations, different indicators of complexity, etc., can be calculated. These quantities enlighten new details of the hierarchical organization of the atomic states. In fact, states with the same energy can display, for instance, different values of complexity. This is the behavior shown by the simplest atomic system, that is, the hydrogen atom (H -atom). Now, we present the calculations for this system [36]. Other works concerning with the complexity of hydrogen atoms were also made by Dehesa et al. [37]. The non-relativistic wave functions of the H-atom in position space (r=(r, Ω ), With r the radial distance and Ω the solid angle) are:

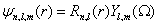(1.13)

Where Rn,l (r) is the radial part and Yl,m (Ω ) is the spherical harmonic of the atomic state determined by the quantum numbers (n, l, m). The radial part is expressed as [35]

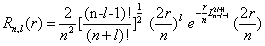(1.14)

being L^β_α(t) the associated Laguerre polynomials. Atomic units are used here.

The same functions in momentum space (p=(p, ˆΩ), with p the momentum modulus and ˆΩ the solid angle) are:

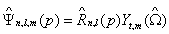(1.15)

Where the radial part ˆR n,l ( p) is now given by the expression [38]

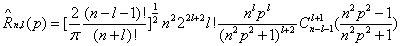(1.16)

With C^β _α(t ) the Gegenbauer polynomials.

Taking the former expressions, the probability density in position and momentum spaces,

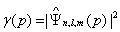, (1.17)

Can be explicitly calculated. From these densities, the statistical complexity and the Fisher-Shannon information are computed. Cr and Cp (Equation: 1.9) are plotted in Figure 1.4 as function of the modulus of the third component m of the orbital angular momentum l for different pairs of (n, l) values. The range of the quantum numbers is: n ≥ 1, 0 ≤ l ≤ n-1, and -l ≤ m ≤ l. Figure 1.4(a) shows Cr for n=15 and Figure 1.4(b) shows Cr for n=30. In both figures, it can be observed that Cr splits in different sets of discrete points. Each one of these sets is associated to a different l value. It is worth to note that the set with the minimum values of Cr corresponds just to the highest l, that is, l=n-1. The same behavior can be observed in Figures 1.4(c) and 1.4(d) for Cp. Figure 1.5 shows the calculation of Pr and Pp (see expression (1.10)) as function of the modulus of the third component m for different pairs of (n, l) values. The second factor, Ir or Ip, of this indicator can be analytically obtained in both spaces (position and momentum). The results are [39]:

Figure 1.4: Statistical complexity in position space, C_r , and momentum space, C_p, vs. |m| for different (n; l) values in the hydrogen atom. C_r for (a) n = 15 and (b) n = 30. C _p for (c) n = 15 and (d) n = 30. All values are in atomic units.

Figure 1.5: Fisher-Shannon information in position space, P_r , and momentum space, P_p, vs. |m| for different (n; l) values in the hydrogen atom. P_r for (a) n = 15 and (b) n = 30. P_p for (c) n = 15 and (d) n = 30. All values are in atomic units.

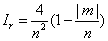(1.18)

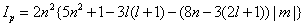(1.19)

In Figure 1.5(a), Pr is plotted for n=15, and Pr is plotted for n=30 in Figure 1.5(b). Here Pr also splits in different sets of discrete points, showing a behavior parallel to the above signaled for C (Figure 1.4). Each one of these sets is also related with a different l value. It must be remarked again that the set with the minimum values of Pr corresponds just to the highest l. In Figures 1.5(c) and 1.5(d), the same behavior can be observed for Pp . Then, it is put in evidence that, for a fixed level of energy n, these statistical magnitudes take their minimum values for the highest allowed orbital angular momentum, l=n-1. It is worth to remember at this point that the mean radius of an (n, l=n- 1) orbital,n, l , is given by [40]

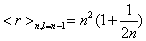(1.20)

that tends, when n is very large, to the radius of the nth energy level, r_Bohr=n² , of the Bohr atom. The radial part of this particular wave function, that describes the electron in the (n, l=n -1) orbital, has no nodes. In fact, if we take the standard deviation, 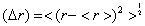, of this wave function, 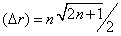, the ratio (Δ r)/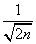becomes for large n. This means that the spatial configuration of this atomic state is like a spherical shell that converges to a semi classical Bohr-like orbit when n tends to infinity. These highly excited H-atoms are referred as Rydberg atoms, that have been intensively studied [41] for its importance in areas as astrophysics, plasma physics, quantum optics, etc., and also in studies of the classical limit of quantum mechanics [42]. We conclude this section by remarking that the minimum values of these statistical measures calculated from the quantum wave functions of the H-atom enhance our intuition by selecting just those orbitals that for a large principal quantum number converge to the Bohr-like orbits in the pre-quantum image. Therefore, these results show that insights on the structural conformation of quantum systems can be inferred from these magnitudes, as it can also be seen in the next sections.

The periodic table

The use of these statistical magnitudes to study the electronic structure of atoms is another interesting application [43-50,20]. The basic ingredient to calculate these statistical indicators is the electron probability density, ρ(r), that can be obtained from the numerically derived Hartree-Fock atomic wave function in the non-relativistic case [45,46], and from the Dirac-Fock atomic wave function in the relativistic case [47]. The behavior of these statistical quantifiers with the atomic number Z has revealed a connection with physical measures, such as the ionization potential and the static dipole polarizability [44]. All of them, theoretical and physical magnitudes, are capable of unveiling the shell structure of atoms, specifically the closure of shells in the noble gases. Also, it has been observed that statistical complexity fluctuates around an average value that is non-decreasing as the atomic number Z increases in the non-relativistic case [46,47]. This average value becomes increasing in the relativistic case [47]. This trend has also been confirmed when the atomic electron density is obtained with a different approach [51]. In another context where the main interactions have a gravitational origin, as it is the case of a white dwarf, it has also been observed that complexity grows as a function of the star mass, from the low-mass non-relativistic case to the extreme relativistic limit. In particular, complexity for the white dwarf reaches a maximum finite value in the Chandrasekhar limit as it was calculated by Sañudo and López-Ruiz [52]. An alternative method to calculate the statistical magnitudes can be used when the atom is seen as a discrete hierarchical organization. The atomic shell structure can also be captured by the fractional occupation probabilities of electrons in the different atomic orbitals. This set of probabilities is here employed to evaluate all these quantifiers for the non-relativistic (NR) and relativistic (R) cases. In the NR case, a non-decreasing trend in complexity as Z increases is obtained and also the closure of shells for some noble gases is observed [53, 54]. For the NR case, each electron shell of the atom is given by (nl) w [55], where n denotes the principal quantum number, l the orbital angular momentum (0 ≤ l ≤ n- 1) and w is the number of electrons in the shell (0 ≤ w ≤ 2(2l + 1)). For the R case, due to the spin-orbit interaction, each shell is split, in general, in two shells [56]: (nl j_)^w−, (nl j+)^w+ ,where j_±=l ± 1/2 (for l=0 only one value of j is possible, j=j+=1/2) and 0 ≤ w± ≤ 2 j± + 1. As an example, we explicitly give the electron configuration of Ar(Z=18) in both cases,

Ar(NR) : (1s)2 (2s)2 (2 p)6 (3s)2 (3 p)6, (1.21)

Ar(R) : (1s1/2)2 (2s1/2)2 (2 p1/2)2 (2 p3/2)4 (3s1/2)2 (3 p1/2)2 (3 p3/2)4.(1.22)

For each atom, a fractional occupation probability distribution of electrons in atomic orbitals {pk}, k=1, 2, . . . , Π, being Π the number of shells of the atom, can be defined. This normalized probability distribution {pk} (1) k Σ p = is easily calculated by dividing the superscripts w± (number of electrons in each shell) by Z, the total number of electrons in neutral atoms, which is the case we are considering here. The order of shell filling dictated by nature [55] has been chosen. Then, from this probability distribution, the different statistical magnitudes (Shannon entropy, disequilibrium, statistical complexity and Fisher-Shannon entropy) are calculated. In order to calculate the statistical complexity C=H·D, with H=e^S, we use the discrete versions of the Shannon entropy S and disequilibrium D:

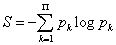(1.23)

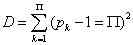(1.24)

To compute the Fisher-Shannon information, P=J · I, with, the discrete 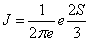version of I is defined as [53,54]

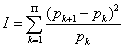(1.25)

where p^Π+1=0 is taken.

The statistical complexity, C, as a function of the atomic number, Z, for the NR and R cases for neutral atoms is given in Figures 1.6 and 1.7, respectively. It is observed in both figures that this magnitude fluctuates around an increasing average value with Z. This increasing trend recovers the behavior obtained by using the continuous quantum-mechanical wave functions [46,47]. A shell-like structure is also unveiled in this approach by looking at the minimum values of C taken on the noble gases positions (the dashed lines in the figures) with the exception of Ne(Z=10) and Ar(Z=18). This behavior can be interpreted as special arrangements in the atomic configuration for the noble gas cases out of the general increasing trend of C with Z. The Fisher-Shannon entropy, P, as a function of Z, for the NR and R cases in neutral atoms is given in Figures 1.8 and 1.9, respectively. The shell structure is again displayed in the special atomic arrangements, particularly in the R case (Figure 1.9) where P takes local maxima for all the noble gases (see the dashed lines on Z=2, 10, 18, 36, 54, 86). The irregular filling (i.f.) of s and d shells [55] is also detected by peaks in the magnitude P, mainly in the R case. In particular, see the elements Cr and Cu (i.f. of 4s and 3d shells); Nb, Mo, Ru, Rh, and Ag (i.f. of 5s and 4d shells); and finally Pt and Au (i.f. of 6s and 5d shells). Pd also has an irregular filling, but P does not display a peak on it because the shell filling in this case does not follow the same procedure as the before elements (the 5s shell is empty and the 5d is full). Finally, the increasing trend of P with Z is clearly observed. Then, it is found that P, the Fisher- Shannon entropy, in the relativistic case Figure1.9 reflects in a clearer way the increasing trend with Z, the shell structure in noble gases, and the irregular shell filling of some specific elements. The same method that uses the fractional occupation probability distribution is applied in the next section to other many particle systems, the metallic clusters that have also been described by a shell model.

Figure 1.6: Statistical complexity, C, vs. Z in the non-relativistic case (C^NR). The dashed lines indicate the position of noble gases. For details, see the text.

Figure 1.7: Statistical complexity, C, vs. Z in the relativistic case (CR). The comments given in Figure 1.6 are also valid here.

Figure 1.8: Fisher-Shannon entropy, P, vs. Z, in the non relativistic case (P^NR). The dashed lines indicate the position of noble gases. For details, see the text.

Figure 1.9: Fisher-Shannon entropy, P, vs. Z, in the relativistic case (P^R). The comments given in Figure 1.8 are also valid here.

The metallic clusters

The calculation of information theory measures of complexity on quantum systems [45,51,57,58] deserves a special attention such as reveals its application to atoms or nuclei unveiling some properties of the hierarchical organization of these many-body systems [52,54]. In particular, entropic products such as Fisher-Shannon in-formation and statistical complexity present two main characteristics when applied to the former systems. On one hand, they display an increasing trend with the number of particles, electrons or nucleons. On the other hand, they take external values on the closure of shells. Moreover, in the case of nuclei, the trace of magic numbers is displayed by these statistical magnitudes [59]. The basic ingredient to calculate these statistical magnitudes is the particle probability density that can be obtained from the numerically derived Hartree Fock wave function or a density functional-theory (Kohn-Sham equations) for molecules [60]. An alternative method to calculate these indicators can be used when the multi-particle system is seen as a discrete hierarchical organization. In this case, the shell structure of the multi-component system can also be captured by the fractional occupation probabilities of the particles in the different orbitals. In atomic physics, these statistical quantifiers have revealed a connection with physical measures, such as the ionization potential and the static dipole polarizability [44]. All of them, theoretical and physical magnitudes, are capable of unveiling the shell structure of atoms, specifically the closure of shells in the noble gases.

Following this line of work, metal clusters are other multiparticle systems that merit our attention. These are useful quantum systems to understand how the physical properties evolve in the transition from atom to molecule to small particle to bulk solid [61,62]. They also present a shell structure where the statistical indicators before mentioned can be applied. As in the case of atoms and nuclei, the fractional occupation probabilities of valence electrons in the different orbitals can capture the shell structure. This set of probabilities can be used to evaluate the statistical quantifiers for metallic clusters as a function of the number of valence electrons. Similar calculations have been reported in the previous section for the electronic atomic structure [52,54] and for nuclei [59]. From this perspective, the multiparticle character of the system is not taken into account since the cluster is treated in a strict single particle picture where at each step the probability of a given electron to occupy one of the partially filled shells is calculated. By following this method, we undertake here the calculation of statistical complexity and Fisher-Shannon information for metal clusters. The jellium model provides an accurate description of some simple metal clusters. In this model, a valence electron is assumed to interact with the average potential generated by the other electrons and the ions [61,62]. The confinement potential in the Schrodinger equation leading to shell structure is taken as a potential intermediate between the three-dimensional harmonic oscillator and the three dimensional square well. This yields a filling of shells with a number N of valence electrons given by the series: 2, 8, 18, 20, 34, 40, 58, 68, 70, 92, 106, 112, 138, 156, 166, 168, 198, 220 and so on. Each shell is given by (nl)w, where l denotes the orbital angular momentum (l=0, 1, 2, . . .), n counts the number of levels with that l value, and w is the number of valence electrons in the shell, 0 ≤ w ≤ 2(2l+1). As an example, we explicitly give the shell configuration of a metal cluster formed by N=58 valence electrons. It is obtained:

(N=58) : (1s)² (1 p)⁶ (1d)¹⁰ (2s)² (1 f )¹⁴ (2 p)⁶ (1g)¹⁸. (1.26)

The fractional occupation probability distribution of electron orbitals {pk}, k=1, 2, . . . , Π, being Π the number of shells, is easily found by dividing the superscripts w by the total number N of electrons. This normalized probability distribution {pk} 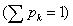is here defined in the same way as it has been done in other cases (in the former section) applied to calculate these magnitudes in atoms and nuclei [52,54,59]. Then, from this probability distribution, the different statistical magnitudes, Shannon entropy, disequilibrium, Fisher information, statistical complexity and Fisher-Shannon entropy, can be obtained. Other generalized magnitudes that have recently appeared in the literature could also be tested in this type of systems [63,64]. Here, we undertake the calculation of entropic products, a statistical measure of complexity C and the similar indicator [24,65,66] the Fisher-Shannon entropy P, that result from the product of two statistical quantities, C=H · D and P=J · I, where H=e^S and 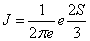. The expressions for S, D and I are the same that we have used in the former section in the Equations 1.23, 1.24 and 1.25, respectively. The statistical complexity, C, of metal clusters as a function of the number of valence electrons, N, is given in Figure 1.10. We can observe in this figure that this magnitude fluctuates around a slightly increasing average value N. This trend is also found for the electronic structure of atoms [52] and for the shell structure of nuclei [59], reinforcing the idea that in general complexity increases with the number of units forming a system. However, the shell model supposes that the system encounters certain ordered rearrangements for some specific number of units (electrons or nucleons) that coincide with closed shells. In the present case, this fact is reflected by the notable increase of C in the metal clusters with one valence electron more than those with closed shells, which are indicated in Figure 1.10, just as happens for atoms when one electron is added to noble gases or when one nucleon is added to a closed shell in nuclei. Observe that some major shells do not show local minima at their closing. This effect is due to the number of valence electrons belonging to each shell: a shell with a few valence electrons displays a local minimum of C when it is closed, but this is not the case when the number of valence electrons in a shell increases. A similar decreasing behavior with N can be observed for D (Figure 1.11). The Fisher-Shannon entropy, P, of metal clusters as a function of N is given in Figure 1.12. It presents an increasing trend with N. The spiky behavior of C provoked by the shell structure is still present for P but becomes smoother in this case. P displays notable peaks only at a few N related with the filling of some major shells, concretely at the numbers 2, 8, 18, 34, 58, 92, 138, 198. It must be remarked that, similarly as happens with C, the maximum values of P are taken on the nuclei with one unit more than the former series, although now the difference is slightly appreciable. Only peaks at 20 and 40 disagree with the sequence of magic numbers {2, 8, 18, 20, 34, 40, 58, 92, 138, 198} obtained from experimental data, for instance, for Na clusters [67] and for Cs clusters [68,69]. Let us observe that the magic numbers are basically marked as extreme by the Fisher information such as can be seen in Figure 1.13. This is an alternative way to predict the magic numbers respective to other methods, such as the 3-dimensional q-deformed harmonic oscillator model [70]. In summary, the behavior of the statistical complexity C and the Fisher-Shannon information P with the number of valence electrons in metal clusters here reported shows the increasing trend of these magnitudes with the number of valence electrons, N. The method that uses the fractional occupation probabilities has been applied to calculate these statistical indicators. As in the case of atoms and nuclei, the shell structure is well displayed by the spiky behavior of C. On the other hand, P shows a smoother behavior but with relevant peaks just on the major shells that coincide with the series of magic numbers in metal clusters. Therefore, the qualitative study of metal clusters by means of statistical indicators unveils certain physical properties of them. In fact, we can again conclude that this type of statistical measures is able to enlighten some conformational aspects of quantum many-body systems.

Figure 1.10: Statistical complexity, C, vs. number of valence electrons, N. The arrows indicate the positions of closed shells.

Figure 1.11: Disequilibrium, D, vs. number of valence electrons, N. The arrows indicate the positions of closed shells.

Figure 1.12: Fisher-Shannon entropy, P, vs. the number of valence electrons, N. The arrows indicate prominent closed shells that are magic numbers. For details, see the text.

Figure 1.13: Fisher information, I, vs. the number of valence electrons, N. The arrows indicate promi-nent closed shells that are magic numbers.

The crystalline bands

The application of information theory measures to quantum systems is a subject of great interest [45,51,58,71,72]. Some relevant properties of the hierarchical organization of atoms [52,54] and nuclei [59] are revealed when these indicators are calculated on these many-body systems. Also these statistical quantifiers have revealed a connection with physical measures, such as the ionization potential and the static dipole polarizability [44] in atomic physics. All of them, theoretical and physical magnitudes, are capable of unveiling the shell structure of atoms, specifically the closure of shells in the noble gases. A strategy to calculate these indicators is to quantify the discrete hierarchical organization of these multiparticle systems through the fractional occupation probabilities. These probabilities capture the filling of the shell structure of these systems. From them, the different statistical magnitudes are derived. The metallic clusters are another system that has also been studied with this method [73]. As in the case of atoms and nuclei, the shell structure of the valence electrons is well displayed by the spiky behavior of the statistical complexity and the magic numbers are unveiled by relevant peaks of the Fisher-Shannon information. A different strategy to compute these entropic magnitudes is to use the probability density of the quantum system as the basic ingredient. This can be analytically obtained in some cases such as the H-atom [51] or numerically derived in other cases from a Hartree-Fock scheme [46,47] or a density functional-theory for atoms and molecules [60]. Here we address the problem to calculate these statistical indicators in a solid by this last strategy [74]. For this purpose, the band structure of the solid has to be determined. The Kronig-Penney (KP) model [75] is a one-dimensional model of crystalline solids that presents a band structure sharing many properties with band structures of more sophisticated models. Moreover, it also has the advantage that allows to analytically finding such electronic band structure. The KP model considers that electrons move in an infinite one-dimensional crystal where the positive ions are located at positions x=na/2 with n=±1, ±2, . . ., generating a periodic potential of period a. A simplified version of the KP model is obtained when this periodic potential is taken with the form of the Dirac comb [76]:

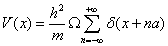(1.27)

Where h¯ is the Planck constant, m is the electronic mass and Ω is the intensity of the potential. In this case, the spatial part Ψ (x) of the electronic wave function is determined from the time independent Schrodinger equation:

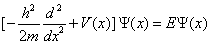(1.28)

Where the eigenvalue E is the energy of the Eigen state Ψ (x).

For a periodic potential, the Bloch’s theorem [77] establishes the form of the general solution of the Eq. (1.28). This is a plane wave, with wave number K, modulated by a periodic function, u_K (x):

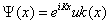(1.29)

Where uK (x) has the periodicity of the crystal lattice: uK (x)=uK (x + a). It implies the following translation property,

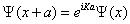(1.30)

Let us observe that we have the case of free electrons when V (x)=0 and the solutions of type (Equation: 1.29) recover the plane wave form with a total wave number k=K, with uK (x)=constant . It suggests that the solution of Equation: 1.28 in the region 0

Ψ(x) = Asin kx + Bcos kx (1.31)

and, by the translation property (1.30), this solution in the region a

Ψ(x) = e^ika[Asin k(x - a) + Bcos k(x - a)] (1.32)

with A, B complex constants and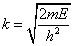

Two boundary conditions must be fulfilled by Ψ at the point: on the one hand, the continuity of the wave function and, on the other hand, the jump in the derivative provoked by the Delta function (Equation: 1.27). This gives the relations: x=a

Ψ(a + 0) = Ψ(a - 0) (1.33)

Ψ' (a + 0) = Ψ' (a - 0) + 2ΩΨ(a) (1.34)

From these boundary conditions applied to the wave functions (Equation: 1.31-1.32), the following homogeneous linear system is obtained for the unknowns A and B:

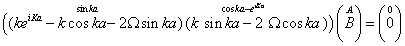(1.35)

To have a non-trivial solution, the determinant of this 2×2 matrix has to be zero. Then, the following quantization relation for k is obtained [76]:

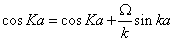(1.36)

The electronic band structure of the one-dimensional crystal is contained in this equation. When K varies its value in the different Brillouin zones, given by (m-1)π ≤ Ka ≤ mπ , with m=1 for the first Brillouin zone, m=2 for the second Brillouin zone, etc., only certain intervals of k are allowed. These intervals for k are the energy bands of the electronic system. The positive and negative parts of these intervals correspond with the positive and negative parts of the Brillouin zones, respectively. In the limit Ω a=0, the free electron problem is recovered, then the solutions are the plane waves with k=K. In the limit Ω a=∞, we have the square well problem, then the wave number of the eigenstates verify sin ka=0. For an intermediate case, 0<Ω a<∞, Eq. (1.36) has to be solved. Concretely, for the particular value Ω a=4, that has also been used in [76], the lower energy bands obtained in this system for k>0 are:

2.154 ≤ ka ≤ π (1st band);

4.578 ≤ ka ≤ 2π (2nd band); (1.37)

7.287 ≤ ka ≤ 3π (3rd band);

10.174 ≤ ka ≤ 4π (4th band):

The bands are symmetrically found for k<0. Observe that, to finally get the wave function of the electronic states, we additionally need the normalization condition to completely determine Ψ (x), except a global phase factor. For our calculations, by taking Ω a=4, we will perform this normalization in the unit cell [0, a]. The basic ingredient to calculate the statistical entropic measures in which we are interested is the probability density of the electronic states. This is given byρ (x) =|Ψ(x) |² . From this density, we proceed to compute the statistical complexity C and the Fisher-Shannon information P. Notice that the wave function Ψ (x) for a given k is transformed in −Ψ (x) for −k, therefore all the magnitudes depending on the density are the same in both cases, and then we reduce our study to the positive part (k>0) of the electronic bands. The entropy, S, and the statistical complexity, C, for the lower electronic bands of the present one-dimensional crystalline solid are given in Figure 1.14 and Figure 1.15, respectively. When this hypothetical solid is in a situation of high conductivity, i.e. when it contains a band that is partially filled and partially empty, it can be observed in the figures that the more energetic electrons attain the highest entropy and the lowest complexity in the vicinity of the halffilled band. This is the point where in general the highest conductivity is also attained. Take, for instance, the real case of the monovalent metals, that include the alkali metals (Li, Na, K, Rb, Cs) and the noble metals (Cu, Ag, Au). These metals present all the bands completely filled or empty, except an only half-filled conduction band [78]. Compared with other solids, these metals display a very high conductivity, that in the cases of Ag and Cu it is the highest in nature. Then, it is remarkable this coincidence at the point of half-filled band where, on the one hand, the entropy and the statistical complexity are extrema for this model of solids and, on the other hand, the conductivity reaches its upper values for the real cases of monovalent metals.

Figure 1.14: Shannon entropy, S, vs. the adimensional wave number, ka, for k > 0. Only the four lower electronic bands given in expression (1.37) are shown.

Figure 1.15: Statistical complexity, C, vs. the adimensional wave number, ka, for k > 0. Only the four lower electronic bands given in expression (1.37) are shown.

Now, we check that other statistical entropic measures also display this behavior when the solid has half-filled bands. Let us take, for instance, the Fisher-Shannon information, P, that has been applied in different contexts [24,79] for atomic systems. Observe in Figure 1.16 the confirmation of the previous results obtained in Figures 1.14 and 1.15 for S and C, in the sense that the external values of P for this model of solids are also reached at the half-filling band points. The former calculations are done orbital by orbital, i.e. thinking that the solid is a set of individual and independent orbitals, each one identified by its own wave number k. We can change the point of view of the problem and to think that the solid stands in some kind of collective state whose probability density ρt(x) is the normalized sum of all the allowed electronic densities obtained from the orbitals with wave numbers in the interval [kmin, kmax ]; kmin will be the minimal electronic wave number of the solid, i.e. the lowest k obtained in the first band, and kmax will be the upper k corresponding to the most energetic electron of the solid. The expression for ρ_t(x) is

Figure 1.16: Fisher-Shannon entropy, P, vs. the adimensional wave number, ka, for k > 0. Only the four lower electronic bands given in expression (1.37) are shown.

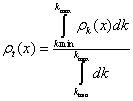(1.38)

Observe that ρt(x) is normalized in the interval [0,a], 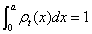and that in the present model of solid k_min=2.154 as given in formulas (1.37). The calculation of the statistical complexity C_t for this ρt(x) is presented in Figure1.17. In this case, the minimal values of C_t are also located in the vicinity of the half-filled electronic bands such as the behavior of C for the individual orbitals shown in Figure 1.15. In the hypothetical limit case of a solid where kmax a » 1, let us remark that the density ρ_t (x) will tend to the uniform density and then the lowest value of complexity, C_t=1, can be reached, as it can be seen in Figure 1.17. In summary, this calculation once again puts in evidence that certain conformational properties of many-body systems are reflected by the behavior of the statistical complexity C and the Fisher-Shannon information P. In the present study, the electronic band structure of a model of solids has been unfolded and the measurement of these magnitudes for such a model has been achieved. It is remarkable the fact that the external values of C and P are attained on the configurations with half-filled bands, which is also the electronic band configuration displayed by the solids with the highest conductivity, let us say the monovalent metals. Therefore, the calculation of these statistical indicators for a model of solids unveil certain physical properties of these systems, in the same way that these entropic measures also reveal some conformational aspects of other quantum many-body systems, such as it has been shown in the previous sections.

Figure 1.17: Accumulated statistical complexity, Ct , vs. the adimensional wave number, ka, for k > 0. Only the four lower electronic bands given in expression (1.37) are shown.

The traveling densities

The behavior of the statistical complexity in time-dependent systems has not been broadly investigated. A work in this direction was done in [22] where a gas decaying toward the asymptotic equilibrium state is studied. It was found that this system goes towards equilibrium by approaching the maximum complexity path, which is the trajectory in distribution space formed by the distributions with the maximal complexity. Then, from a physical point of view, it has some interest to study the external behavior of statistical magnitudes in time dependent systems. In this section, we start by studying the statistical complexity C in a simplified time-dependent system ρ(x,t) composed of two onedimensional (variable x) identical densities that travel in opposite directions with the same velocity v, one of them, ρ₊(x, t), going to the right and the other one, ρ_-(x, t) going to the left. That is

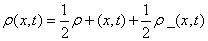(1.39)

with the normalization condition 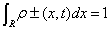that implies the normalization of ρ(x,t), and the initial condition ρ₊(x,0)=ρ_-(x,0). Then, we calculate the statistical complexity C for two Gaussian, two rectangular and two triangular traveling densities in [80-82]. Specifically, the shape of ρ(x,t) presenting the maximum and minimum C is explicitly shown for all these cases.

Gaussian traveling densities: Here, the two one-dimensional traveling densities that compose system (Equation: 1.39) take the form:

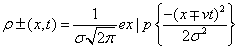(1.40)

where σ is the variance of the density distribution.

The behavior of complexity, C_G , as a function of the adimensional quantity 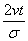is given in Figure 1.18. Let us observe that C_G presents a minimum. The shape of system (Equation: 1.39) for this minimum complexity case is plotted in a dimensional scale in Figure 1.19.

Figure 1.18: Statistical complexity, C_G, vs. the adimensional separation, 2vt=σ, between the two traveling Gaussian densities defined in Equation. (1.40). The minimum of C_G is reached when 2vt=σ = 2.91. The dashed line indicates the value of complexity for the normalized Gaussian distribution.

Figure 1.19: Shape of the density (1.39) in adimensional units that presents the minimum statistical complexity when the two traveling Gaussian densities defined in (1.40) are crossing. Notice that the value of the dimensional separation between the centers of both Gaussian distributions must be 2.91.

Rectangular traveling densities: Now, the two one-dimensional traveling densities that compose system (Equation: 1.39) take the form:

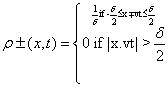(1.41)

where δ is the width of each distribution. For this case, the complexity, C_R, can be analytically obtained. Its expression is:

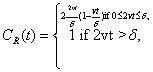(1.42)

The behavior of C_R as a function of the adimensional quantity 2vt/δ is given in Figure 1.20. Let us observe that C_R presents a maximum. The shape of system (Equation: 1.39) for this maximum complexity case is plotted in a dimensional scale in Figure 1.21.

Figure 1.20: Statistical complexity, C_R, vs. the adimensional separation, 2vt=δ, between the two traveling rectangular densities defined in Equation (1.41). The maximum of C_R is reached when 2vt=δ = 0.557. Observe that the normalized rectangular distribution has C_R = 1.

Figure 1.21: Shape of the density (1.39) in a dimensional units that presents the maximum statistical complexity when the two traveling rectangular densities defined in (1.41) are crossing. Notice that the value of the a dimensional separation between the centers of both rectangular distributions must be 0.557. Then, the width of the overlapping between both distributions is 0.443.

Triangular traveling densities: The two one-dimensional traveling densities that compose system (Equation: 1.39) take the form in this case:

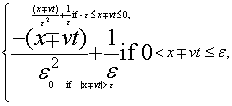(1.43)

The behavior of complexity, C_T , as a function of the a dimensional quantity 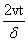is given in Figure 1.22. Let us observe that CT presents a maximum and a minimum. The shape of system (Equation: 1.39) for both cases, with maximum and minimum complexity, are plotted in an a dimensional scale in Figures 1.23 and 1.24, respectively. Then, in this section, we have studied the behavior of the statistical complexity as a function of time when two traveling identical densities are crossing each other. Three cases have been analyzed: Gaussian, rectangular and triangular densities. The Gaussian case presents a particular configuration with minimum complexity. The rectangular case displays a particular configuration with maximum complexity.

Figure 1.22: Statistical complexity, C_T , vs. the adimensional separation, 2vt=ε, between the two trav-eling triangular densities given in Equation (1.43). The maximum and minimum of C_T are reached when 2vt=ε takes the values 0.44 and 1.27, respectively. The dashed line indicates the value of complexity for the normalized triangular distribution.

Figure 1.23: Shape of the density (1.39) in a dimensional units that presents the maximum statistical complexity when the two traveling triangular densities defined in (1.43) are crossing. Notice that the value of the a dimensional separation between the centers of both triangular distributions must be 0.44.

Figure 1.24: Shape of the density (1.39) in a dimensional units that presents the minimum statistical complexity when the two traveling triangular densities defined in (1.43) are crossing. Notice that the value of the a dimensional separation between the centers of both triangular distributions must be 1.27.

The triangular case shows an intermediate behavior between the two former cases with two particular configurations, one of them with maximum complexity and the other one with minimum complexity. In general, all these configurations with external complexity cannot be analytically obtained and a careful computational study is required in order to determine them.

Different definitions of complexity have been proposed in the context of computational and social sciences. In this review, we focus our attention in one of them, the statistical LMC complexity C, that has been applied in many different problems due to its generality and its operability to be computed without requiring a big amount of calculations. Several applications in quantum systems are recorded here. It is put in evidence that certain conformational properties of the quantum systems are reflected by the behavior of this statistical magnitude C. In the first application, we have concluded by remarking that the minimum values of C calculated from the quantum wave functions of the H-atom can select just those orbitals that for a large principal quantum number converge to the Bohr-like orbits in the pre-quantum image. In the second application, we have found that if the fractional occupation probabilities of electrons in atomic orbitals, instead of the continuous electronic wave functions, are used to calculate the complexity, the shell structure in noble gases and the irregular shell filling of some specific elements is also reflected in the behavior of C. In the next application, a similar behavior is displayed by the metal clusters. The increasing trend of C with the number of valence electrons and the shell structure of the clusters is found in the spiky behavior of C. In the case of the band structure of a model of solids, it has been remarked the fact that the external values of C is attained on the configurations with half-filled bands, which are also the electronic band configurations displayed by the solids with the highest conductivity, that is, the monovalent metals. A last example is presented where the behavior of C as a function of time when two traveling identical densities are crossing each other is computed. Different cases were analyzed: Gaussian, exponential, rectangular, triangular and gamma densities. The configurations with external complexity were found for all these cases. This is a calculation that in general cannot be analytically obtained and that needs a careful computational study in order to determine the configurations with maximum or minimum C. In summary, the results here reported show that the statistical entropy-based magnitudes provide a complementary and useful way of thinking ready to be applied at a quantum level and able to enlighten conformational aspects of quantum many body systems.