In recent years, the development of bio-techniques allows researchers to collect different types of data from an experiment, such as gene expression data, SNP data, and copy number variations (CNVs) data. A better result could be generated based on combining multiple types of data than using any individual data. Combined analysis with different data typesof genome-wide measurements is not a new concept, but how to combine them efficiently for biological discovery is always challenging. A web based platform, called Magellan, was developed for the integrated analysis of DNA copy number and expression data in ovarian cancer [1]. The significant correlation between gene expression and patient survival has been found by Magellan. Troyanskayaet al. [2] developed a Bayesian framework to combine heterogeneous data sources for predicting gene function. Improved accuracy of the gene groupings has been achieved compared with microarray analysis alone. Kernel-based statistical learning algorithms were also used in the combine analysis of multiple genome-wide datasets [3]. Some combined analysis methodsneed the datasets to have the same distribution [4]; one has to transform the datasets to be the same distribution before the analysis. Recently, an integrative approach combining linkage, gene expression, and association has been reported to identify candidate genes regulating BMD [5]. The combined analysis approach proposed in this work has no specific requirement for the data types or data distributions. In order to test the effectiveness of our approach, we applied it to the subtyping of gilomas.

Gliomas are tumors that start in the brain or spine and arise from glial cells [6]. Gliomas are the most common type of primary brain tumors in adults [7]. The classification of gliomas can be based on cell type, grade and location. For instance, gliomas can be classified into low-grade and high-grade determined by pathologic evaluation of the tumor. In this study, we define the subtypes based on genetic and molecular signatures according tothe reference [7].

The classification of glioma subtypes has attracted a lot of attentions and has been investigated by many research groups. Most of the works have been based on gene expression data. It was reported that four subtypes of gliomas, oligodendroglioma, anaplastic oligodendroglioma, anaplastic astrocytoma and glioblastomamultiforme, can be distinguished by only two-gene or three-gene combinations [8]. Nutt et al. [9] built a k-nearest model with 20 features to classify 28 glioblastomas and 22 anaplastic oligodendrogliomas.It was claimed that class distinctions according to the model were significantly associated with survival outcome (P=0.05). Chakrabortyet al. [10] considered several Bayesian classification methods to classify gliomas with gene expression data. A Bayesian variable selection scheme was also proposed for gene selection.Noushmehret al. [12] found a distinct subset of samples in The Cancer Genome Atlas (TCGA) glioma samples displaying concerted hypermethylation at a large number of loci. They took it as evidence that a glioma-CpG island methylator phenotype exists. Verhaaket al. [12]classified glioma into four subtypes: Proneural, Neural, Classical, and Messenchymal, based on gene expression data. MRI data have also been used in the classification of gliomas [13,14]. However, to the authors’ best knowledge, few researchers have combined two or more than two types of data to improve thegliomasclassification.

Therefore, a novel approach that can combine multiple data sets is needed for improved classification. Compressed sensing (CS), also called compressive sampling, has been developed recently in statistics and signal processing, and becomes a powerful tool for data analysis. We recently used CS method to classify chromosomes from multicolor fluorescence in-situ hybridization (M-FISH) images[15], as well as integrated analysis of copy number data and gene expression data for identifying gene groups susceptible to cancers[16]. In these studies, we demonstrated the advantages of the CS methods in compact representation of combined genomic data, resulting in higher classification accuracy.

The work described in this work is to develop a CS based integration and classification methods and apply them to identify the subtyping of gliomas. The resultsdemonstrate that the proposed methodscan significantly improve the classification accuracy of gliomascompared to individual gene expression orCNVs data analysis.

Data Collection

The data in this study is publicly available from the website of National Cancer Institute (https://caintegrator.nci.nih.gov/ rembrandt/home.do). Two unsupervised methods had been used to analyze the six glioma subtypes based on the gene expression data of the patients[7]. In our study, we classify the six Glioma subtypes by integrated analysis of both gene expression and CNVs data. The overview of the six hierarchically nested subtypes of gliomas is shown in Figure 1.

Figure 1: The hierarchical structure of the six subtypes of gliomas.

We collected a dataset that has 56 samples (patients) with both gene expression data (54675 genes for each sample) and CNV data (758 probes for each sample). Eight samples belong to theOligodendroglioma-rich(O) main type that has 4 OAs and 4 OBs. For the rest 48 samples,Glioblastoma-rich (G), we have 27 GAs (10 GA1s and 17 GA2s) and 21 GBs (13 GB1s and 8 GB2s).

According to the structure of the six subtypes described in Figure 1, we used divisive(TOP-DOWN) algorithm to subtype each of the 6 classes.At the top level, the data are classified into two main types O and G; then those two subtypes are further classified, until6 subtypes are obtained at the bottom level.Sparse representation clustering (SRC) method proposed by usis applied to select informative variables (IVs) (genes or probes) for the subtyping of gliomasin the analysis. SRC algorithm was obtained from compressed sensing (CS) theory, which aims to approximate a sparse solution of y = Ax in a given underdetermined matrixA.

Feature selection

To distinguish the two groups (e.g., O and G), it is helpful to extract significant features from the overall gene expression and CNVs data, respectively. For each gene or probe, we extracted 4 features: the standard deviation of each group (Std₁ and Std₂), the absolute value of the mean difference of the two groups (MD), and the Pearson’s linear correlation coefficient (Corr). Thus for i-th variable, we have a 4 dimensional feature vector as follows:

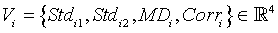                                                              (1)

Where i=1,2,...N, and N is the number of genes/CNVs. Each feature is normalized by its overall maximum value so that eachentry of . Vi ∈[0,1] A number of MIVscan beselected accordingly, yielding M << N. The detail of the feature selection can be found in reference [17]. After the normalization, we get the feature dataset as the input of SRC algorithm for the selection of significant genes with small Std₁ and Std₂, high MD and Corr.

SRC algorithm

In CS theory, if a signal 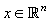is sparse, it could be recovered stably by its measurements Ax = y . This can be formulated as solving the following optimization problem:

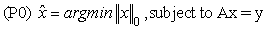                                                                  (2)

Where 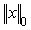is l-0 norm, 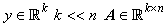. This is an NP hard problem bytraversing all possible entries for x. The l-1 normis used instead by minimizing the nonzero numbers, which can be considered as a linear programming problem:

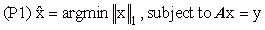                                                                  (3)

Where 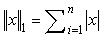The solution path of this problem has a piecewise-linear-property [18], and can be solved with k-steps when x is sparse enough, and A is under certain condition [19,20].

The basic problem in SRC is to use labelled training samples (included in A) from distinct classes to correctly determine the class to which a new test sample belongs. If we design 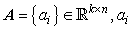, a_i is a positive unite vector with 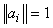, a new unclassified sample 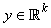will result in an estimate of sparsesolution 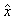, whose non-zero entries correspond to a particular cluster.

Sparse Representation-based clustering (SRC):

1. Input characteristic matrix A with vectors of sdifferent clusters and a test sample y∈R^k×1.

2. Normalize the columns ofAto have unit l-2 norm.

3. Solve the l-1 norm minimization problem (P1) defined by Equation (3).

4. Calculate the vector angle θ_i ( y, Aδ_i (x)) , i∈{1,2,..., s} , where δ_i (x) is a mask function that maps x to a sparse vector, with non-zero entries in the i-th group.

5. Identity (y) = arg min_i (θ_i ).

The details of the SRC algorithm can be found in reference[16].

Transformation matrix design

Todesign a transformation matrix A, several methods have been proposed [19], such as incoherent matrices, random projection matrices, etc. In this study, we propose a method of designing Aby considering all possible classes in a subtyping work.

If m number of features is used for clustering, there will be c = 2^m −1 possible groups, with characteristic matrix A = {A_k }, and k = 1,...,c. We label each group with a column vector V_k ∈ R^{m ×1} being given a binary value, designating different combinations of 1 and 0. Then we design characteristicmatrix of the k-th group 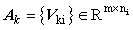, where i = 1,..., n_i , and n_i > m ; V_ki =V_k +V₀ , and V₀ is a random vector with small amplitude; V_ki and have the relation of 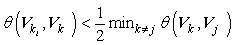, which guarantees that each column vectoris corresponding to itsgroups only.

represented by characteristic matrix A_k = {V_ki} , it requires that rank (A_k ) = m, where k = 1,...,c .In addition to the requirements mentioned above, a valid for the SRC based classifiershould have a sparse solution whose nonzero entries concentrate mostly on one group, while that of an invalid vector with nonzero entries spread evenly over all groups. To quantify this observation, the Sparsity Concentration Index (SCI) [21] shown in Eq. (4) is introduced to validate A to measure how concentrated the feature vectors are on a particular class in the dataset.

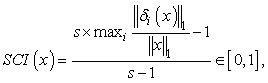                                                                 (4)

Wheres is the number of classes, δ_k (x) is a mask function that that maps x to a sparse vector, with non-zero entries in the i-th group. For a solution found by the SRC algorithm, if SCI () = 1 , the feature vector y is represented using vectors only from a single class; if SCI (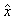) = 0 , the sparse coefficients are spread evenly over all classes. We choose a threshold and accept a vector as valid if SCI (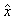) >τ ; otherwise, reject it as invalid.

Compressed sensing based classifier

The training of transformation matrix can be formulated as a sparse representation problem as shown in Eq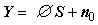. (5),

                                  (5)

Where 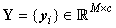are the gene expressions of selected genes for the total samples/patients; 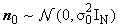is i.i.d. Gaussian noise; 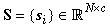are the gene expressions of all the genes for the total samples/patients, and M << N. The matrix 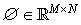is a sparse transformation matrix. The linear system given by (5) is an underdetermined sparse system, which can be solved by using L-1 norm minimization algorithm.

A CS based classifier is developed to classify the glioma subtypes. To testify whether a given vector 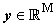belongs to a known signal 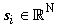or not, we set the hypothesis as follows[22]:

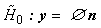
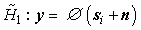                       (6)

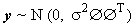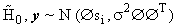From (6), we have under under 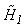, which gives:

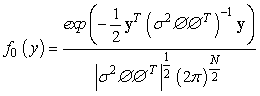     (7)

and

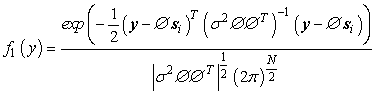              (8)

Thus, the likelihood ratio test is: if 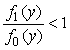, y is under 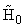; otherwise, y is under 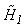. The likelihood ratio test can be simplified by taking a logarithmand the compressive classification 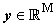of can be derived as follows.

Define compressive detector 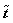as:

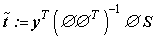(9)

Where 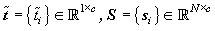, i=1,2, …, c.

It has been proven by reference [18] that under the condition of :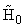

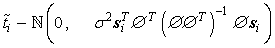                                                               (10)

While under the condition of :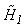

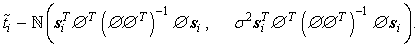                            (11)

We then calculate the differences of the standard score of 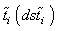under the two conditions:

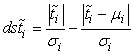                         (12)

Where

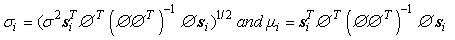
We assign a class ID label to the vector y:

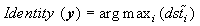          (13)

If Identity (y) is within the range of 1to c1 , y belongs to class1; otherwise, y belongs to class 2. Obviously, our proposed approach can be extended to the classification of multiple classes.

It can be seen that by introducing the sparse transformationmatrix 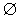, we projected the original signal 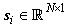to a very smallerdimensionalsignal 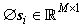. In the following process, instead of dealing with the original signal, we only use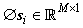d and 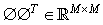in the construction of the compressive detector 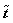and calculation of σ_i and μ_i , leading to a fastclassification.

Cross validationand experimentdesign

A cross validation method, Leave One Out (LOO) [23], is widely used in evaluating the detection accuracy of different classes of subjects. It was employed here to evaluate the efficiency of feature selection and the performances of compressive detector. To find the best LOO accuracy for each subtyping, we calculated the classification accuracy by LOO, based on from 5 to 200 IVs, in three cases:subtyping based on gene expression data, CNVs data and their combinations.

The SRC approach was used to select different numbers of IVs, while the CS based classifier was employed to classify the subtypes of gliomas. Finally, the classification accuracy was calculated by the LOO method. Figure 2 plots the classification accuracies of O and G on the top level of the hierarchical structure for suptyping gliomas. Three results are compared in the Figure 2: classification accuracies calculated by CNVs data, by gene expression data and by the combination of the two types of data.The combined result wascalculated by fixing the number of IVs from CNVs data as the one that achieves the highest accuracy and iterating the number of IVs from gene expression data from 5 to 200 genes. In this specific case, combined analysis doesn’t show any significant advantages compared to the gene expression analysis only.

Figure 2: The classification accuracies of O and G subtypes by using gene expression data only (circle) and the combined data (square), corresponding to different numbers of IVs from 5 to 200. For the CNVs data (star), the maximum number of IVs that can be reached is 30 due to the limitation of sample size. In this specific case, combined analysis doesn’t show any significant advantages compared to the gene expression analysis only.

On the second level of the subtyping, the results shown in Figure 3 are for the classificationof GA and GB. The performance of the combined analysis is obviously much better than either individual analysis. The highest classification accuracy of the combined analysis achieves 77.1%, which is higher than 70.8% from the gene expression. In Figure 4, the combined classification rate can beas high as 100% for the subtyping of OA and OB compared to the highest classification rate of 87.5% from the gene expression data, individully.

Figure 3: The classification accuracies of GA and GB subtypes by using CNVs data (star), gene expression data (circle) and the combined data of the two (square), corresponding to different numbers of IVs from 5 to 200. Note that the combined analysis can reach higher accuracies than either individual analysis.

Figure 4: The classification accuracies of OA and OB subtypes by using gene expression data (circle) and the combined data of the two (square), corresponding to different numbers of IVs from 5 to 200. For the CNVs data (star), the maximum number of IVs that can be reached is 60 due to the limitation of the sample size. Note that the combined analysis can reach higher accuracies (the highest 100%) than either individual analysis.

On the bottom level, in Figure 5, it can be seenthat the combined data analysis for clasifying GA1 and GA2 has the same highest classification rate, 85.2%, as the individual analysis of gene expression data, but with less IVs. The combined analysis used only 15 IVs to achieve the highest classification accuracy, 50 IVs less compared to the individual gene expression analysis. Figure 6 shows the comparison of the combined analysis and individual analysis for the classification of GB1 and GB2 subtypes. It is shown that the combined analysis yields higher classification accuracy (90.5%) than either individual analysis, 81.0% for gene expression and 76.2% for CNVs.

Figure 5: The classification accuracies of GA1 and GA2 subtypes by using CNVs data (star), gene expression data (circle) and the combined data of the two (square), corresponding to different numbers of IVs from 5 to 200. Note that the combined analysis can have the same highest accuracy as individual gene expression analysis but with less IVs.

Figure 6: The classification accuracies of GB1 and GB2 subtypes by using CNVs data (star), gene expression data (circle) and the combined data of the two (square), corresponding to different numbers of IVs from 5 to 200. Note that the combined analysis can reach higher accuracies than either individual analysis.

It can befoundthat combined analysis performs better than either individual analysis in the classification of OA and OB, GA and GB, GB1 and GB2 in Figure 7. For the other two classification, O and G, GA1 and GA2, the combined method has comparable classification rate with the gene expression data analysis. The classification rate based on the CNVs data is the lowest.

Figure 7: The maximum classification accuracies for the five binary classifications. Note that the classification accuracy of using the CNVs data individual analysis is the worst; the accuracy using gene expression data individual analysis is better and the accuracy of using combined analysis is the best among the three cases.

This paper proposed a CS based method to subtype gliomas by combining gene expression data and CNVs data from the same subject of patients. Experiments have been performed to compare the results of combined analysiswith individual analysis. The calculation results show that the combined analysis achieves a significant improvement of the classification accuracythan using the individual analysis except for the subtyping of O and G types of gliomas.

The different types of genomic data used in this study, e.g., gene expression data and CNVs data have different resolutions and provide different information. Gene expression reveals how the functions of genes change, while CNVs indicate where these functional changes occur in the genome, Thus, the information from different sources could be complementary , which can be used to improve the accuracy of classifying diseases. In the human genome, about half of the detected CNVs overlap with regions which code proteins [24]. Therefore, CNV loci encompassing genes may potentially affect gene expression and subsequently relevant phenotypes [25,26]. They exert their influence by modifying the expression of genes mapping within and close to the rearranged region [27]. The information both from CNV and gene expression shed light on the pathogenesis underlying the complex diseases.The proposed integrated data analysis approach provided an appealing solution to subtype gliomas.

The sample size of the Oligodendroglioma-rich (O) is relatively small (4 OAs and 4 OBs). That could influence the reliability of the result. That is probably the reason why we cannot obtain improved accuracy classification of O and G, even with combined data analysis. It could also explain why the classification results in Figure 4 oscillate, with the accuracies up and down. Those problems could be avoided by increasing the sample size of O subtype.

In summary, the combined analysis method proposed in this work provides an improved way of subtyping gliomas than using an individual data. It has the potential to improve the diagnostic accuracy in the clinical practice.

This work has been supported by the NIH grant R21 LM010042 and NSF grant. The authors thank Dr. Aiguo Li and Dr. Howard A. Fine from National Cancer Institute for their great help.