
Journal of Fundamentals of Renewable Energy and Applications
Open Access
ISSN: 2090-4541

ISSN: 2090-4541
Short Communication - (2020)Volume 10, Issue 5
Solar energy is one of the important types of renewable energy sources that have attracted many researchers around the world to work on. Currently, the conversion and utilization of solar energy are mainly done in two ways. The first is the conversion of solar energy through semiconductor photovoltaic (PV) devices, and the second is the conversion of solar energy into heat by thermal collectors.
As it is known, in solar photovoltaic systems most of the energy (approximately 80%) is not converted into electric energy but is converted into thermal energy, which increases the operating temperature of silicon semiconductor solar cells. With heating, the efficiency of solar cells decreases (by 0.5% with each 10C increase in temperature), which is an inherent characteristic of solar cells [1]. On bright sunny days, the temperature of solar cells can reach 1000C. In this case, the efficiency of the cells is reduced by 40%. That is to say if in the standard test conditions (250C), carried out by the manufacturer, the solar module has an efficiency of 17%, in the case of a bright summer sun, it can decrease and accept the value only of about 10%. It is obvious that due to the effect of this phenomenon the power of the solar module and the amount of electricity generated are decreased. Thus, the solar module with a rated power of 300 Watts due to the heating can have power only of 180 W.
To address this problem, different solar PV modules cooling systems are investigated, developed, and employed. These systems are cooling the PV modules by different methods and techniques. Unfortunately, there is no universal approach to assess the effectiveness of applied cooling techniques. In this paper, a method and criterion for the PV modules’ cooling system effectivity assessment are proposed.
Literature survey
Advances in cooling techniques and temperature control of PV panels in general are analyzed and discussed in [2]. In this work different cooling techniques as the passive cooling techniques, active cooling methods, as well as other cooling techniques including the Nano fluids cooling, phase-change material cooling and thermoelectric cooling are discussed.
The other review paper focuses on the improvement of the performance of the small domestic use PV systems by keeping the temperature of the cells as low as possible [3]. The advantages and disadvantages of different cooling systems are analyzed in this work.
There are a big number of publications concerning PV modules cooling by application of hybrid solar PV and Thermal (PVT) systems, which combine two well established renewable energy technologies, solar PV modules and solar thermal collectors, into one integrated component. As a result of this integration, the thermal collector removes generated heat from the solar PV module thereby improving electrical efficiencies [4-7]. In solar PVT systems, the electrical efficiencies have been improved by 4-12% when compared to a solar PV only scenario [8].
The cooling technologies are widely used in solar concentrating PV (CPV) systems whit increased efficiency of electricity generation due to the use of high-efficiency solar cells with one p-n junction or mostly multi-junction cells. In these systems also the operating temperature is one of the main concerns that affect the CPV system [9, 10].
The comprehensive review of architectural, commercial, and industrial usage of CPV system, the recent research developments of different cooling techniques of CPV systems during last few years, including the spectral beam splitting technology, cogeneration power technology, commonly used and promising cooling techniques, active and passive cooling methods is presented in [11].
With a large number of different solar PV modules cooling techniques employed, there is a lack of criteria for the effectivity assessment of the cooling systems. In some publications, the gained power is considered without taking into consideration the surface area of the PV cells. In publication [12] a new approach for photovoltaic module cooling technique evaluation using the temperature-dependent photovoltaic power and the reference power ratio measured at standard test conditions is suggested. In other publications, the total increase in efficiency is measured [13, 14]. This makes it impossible to compare the cooling methods and to assess the application reasonability of the cooling systems and the gained benefit of each employed system. Thus there is a need for a universal value or criterion to assess the effectivity of the given cooling method and technique.
The thermal dependence of the mono/poly-crystalline Si solar cells is defined as [15]:
η=η_(0 ) [1 -β(T-T_0 )], (1)
Where η0 is the reference efficiency of solar cell, which is measured under standard test conditions (STC), β is the temperature coefficient, T is the operating temperature of solar cell (°C), T0 is the reference temperature of the solar cell. Typically the solar cells are rated at T_0=25 °C under illumination of 1 kW/m2 (STC).
The values of η_(0 )and β generally are given by the PV manufacturer. However, they can be obtained from flash tests in which the electrical output of the PV module is measured at two different temperatures for a given solar radiation flux. The temperature coefficient β is different for different types of solar cells. For the most common mono-crystalline and polycrystalline silicon solar cells β = 0.005 / 0C and β = 0.0045 / 0C respectively [15].
The efficiency of a solar cell is determined as the fraction of maximum power which is converted to electricity and incident power of solar radiation and is defined as:
η=P/P_in =P/(AP_sun ), (2)
Where P is the maximum power which is converted into electricity (W), Pin is the incident power of solar radiation (W), A is the surface area of PV modules (m2) and Psun is the solar radiant power per unit area (W/m2).
The temperature dependence of PV power will be: P=P_in η_o [1-β(T-T_0 )]=AP_sun η_0 [1- β(T-T_0 )]. (3)
In accordance with this formula, the power converted to electricity linearly depends on the operating temperature T of the PV module. By application of the cooling system, this temperature is reducing and the PV power is increasing linearly. The power of the cooled PV module can be written as: P_c=P_in η_0 [1-β(T_c-T_0 )], (4)
Where the T_c is the temperature of the cooled PV module. Thus, the following gain in power will be obtained due to the cooling:
ΔP=P_c-P=P_in η_0 β (T-T_c )=P_in η_0 βΔT=AP_sun η_0 β(T-T_c ). (5)
Note that in formula (4) the operation temperature T of PV modules without cooling strongly depends on ambient temperature and solar radiation. An approximate expression for calculating the open back side-mounted module temperature with a wind velocity of 1 m/s, is given by [16]:
T=T_air+S(NOCT-20)/80 , (6)
Where Tair is the ambient temperature, S is the solar radiation (mW/cm2). Module temperature will be lower than this when wind velocity is high, but higher under still conditions.
As follows from this formula the operation temperature of solar cells increases with ambient temperature and solar insulation.
For example, during the hot summer period, for the T_air= 30 0C, Nominal Operating Cell Temperature (NOCT) = 48 0C and S = 100 mW/cm2 as in the bright sunny day, the operation temperature T = 65 0C and at T_air = 40 0C, T = 75 0C. Under these temperatures the PV power will reduce significantly.
The temperature of the cooled PV module T_c in formula (5) also depends on T and consequently to ambient temperature and solar radiation. But it strongly depends also on the inherent properties of the cooling system, and its ability to cool.
Thus, in accordance with expression (5), as it could be expected, the power gain due to the cooling is increasing with the temperature difference ΔT=T-T_c and the ΔT is the main technical parameter characterizing the “quality” of the cooling system.
To assess the effectivity of the applied cooling method it is important also to analyze the economic aspect of the applied method. The expenses that were spent to cool the module are as follows:
C_c=C_cooler+C_instal+N(Cm+Cen), (7)
Where C_cooler is the cost of the cooler applied, Cinstal is the installation cost of cooling system, N is the operation period of cooler (years), Cm is the maintenance cost per year, Cen is the cost per year of energy consumed for cooling. Note that for many cooling technologies the maintenance cost and possible consumed energy cost for cooling can be neglected. In some cooling systems, as in the case of the systems having the autonomous PV module, the cost for consumed energy for cooling is included in the cost of the applied cooler.
The price per gained Watt due to the cooling is:
C_(c⁄w)=C_c/ΔP=C_c/(P_in η_0 βΔT)= C_c/(AP_sun η_0 β(T-T_c ) ) (8)
The efficiency of the employed cooling system can be assessed by comparison of the gained power price C_(c⁄w) with the existing in market price C_(pv⁄w) of the solar PV modules per Watt power, including the installation costs. If the price of gained power is smaller than the market price of PV modules, the application of the cooling system can be considered as effective, and it will be reasonable to implement it. Otherwise, instead of application of the cooling system the additional PV modules can be installed, if the area for these additional modules is available.
Thus the criterion for cooling system effectivity assessment is:
C_(c⁄w)≤C_(pv⁄w) , or C_c/(P_(in ) η_0 βΔT)≤C_(pv⁄w) , or (9)
C_c/(AP_sun η_0 βΔT)≤C_(pv⁄w) .
If the inequality (9) takes place, it will be reasonable to apply the given cooling system. Otherwise, it will not be reasonable to use the cooling system.
The PV module power is included in price C_(pv⁄w)and typically is rated by the producer at T_0=25 °C under the irradiation of 1000 W/m2 (STC). It follows that the cooling system must be tested under the solar radiation of Psun = 1000 W/m2. Thus, for mono-crystalline silicon solar cells with β = 0.005 / 0C and solar radiation Psun = 1000 W/m2, expression (9) can be presented as:
C_c/(5(W/m2x0C )A(m^2 ) η_0 ΔT(°C))≤C_(pv⁄w), (10)
And for poly-crystalline silicon solar cells with β = 0.0045 / 0C: C_c/(4,5(W/m2x0C )A(m^2 ) η_0 ΔT(°C))≤C_(pv⁄w), (11)
where ΔT=T-Tc .
Note that the operating temperature of solar cells T (°C) can be calculated with the use of formula (6) substituting the ambient temperature〖 T〗_air, or it can be measured by using a reference PV module. Thus, by measuring the temperature of the cooled PV module T_c the ΔT will be defined and the efficiency of the cooling system will be assessed using the expressions (9), (10), or (11).
In some cases, when the cooling system does not makes big changes in thermal properties of PV module connected with air convection, as in the case of water cooling by tubing from the rare side of PV modules without application of thermal insulation layer, the temperature T of PV module can be measured without the operation of the cooling system, under the solar radiation of Psun = 1000 W/m2, and the temperature of module Tc can be measured after switching on the cooling system and the ΔT will be defined.
The criterion for cooling system effectivity (10) graphically is presented in Fig. 1. It can be seen from the figure that as much as the difference between market price C_(pv⁄w)of solar PV modules and the price of gained power C_(pv⁄w) as more effective is the cooling system.
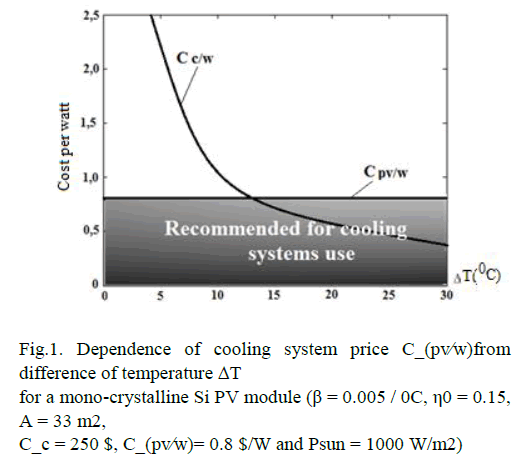
Thus, the formula (9) can be used as the criteria for the given cooling system effectivity assessment. In expression (9) in the case of
C_c/(AP_sun η_0 βΔT)=C_(pv⁄w) , (12)
the cooling system can be applied also, taking into consideration the other advantage of the cooling systems, which is increasing the lifespan of solar PV modules due to the reduction of the operating temperature of PV modules.
For practical use, the criterion (9), (10), (11) for cooling system effectivity assessment can be presented as:
C_c≤〖BC〗_(pv⁄w ), (13)
Where B(W)=5 A(m2) η_o ΔT(0C) (14)
For PV modules with mono-crystalline silicon solar cells, and B(W)=4.5 A(m2)η_o ΔT(0C) (15)
For PV modules with poly-crystalline silicon solar cells. Thus, criterion (9) allows us to define either to apply the cooling system or not. If different cooling systems are compared the more effective system can be defined by the price per gained Watt due to the cooling, using the expression (8). In the case when the increase of lifespan of solar PV modules due to the reduction of operating temperature is needed to take into account, the Levelized Cost of Electricity (LCOE) can be considered as well, where the total lifetime is included.
The criterion for solar PV modules cooling system assessment is proposed. It is based on the determination of the ratio of the price of the cooling system and gained power due to the cooling (the price of the cooling system per Watt of gained power) and comparison of this ratio with the current market price of PV modules per Watt power. This criterion allows us to assess the reasonability of the application of a given cooling method and technology. The suggested criterion allows also to compare the different cooling techniques and to define the more effective one. The proposed criterion can be used by new solar PV modules cooling systems developers and designers.
, DOI: 10.35248/2090-4541.20.10.286
Copyright: This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.