Journal of Physical Chemistry & Biophysics
Open Access

The Distortion and Quantization of the Earth’s Orbit

Author info »

Introduction

The earth revolves around the sun in a stable elliptical orbit. The earth’s orbit will be disturbed by other celestial bodies, and if the disturbance is large enough, it will lead to disastrous consequences for the earth. Certainly, human beings care about related issues, such as: How does the disturbance affect the earth’s orbit? What is the geometrical feature of disturbed orbits? How much energy does it take to cause a devastating disaster? The perturbation theory of classical mechanics cannot provide satisfactory solutions to the problems.

A novel idea to solve the above problems comes from a theory of real particles [1-9]. The real particle theory treats the earth/ solar system as a two-body cluster with a similar structure to hydrogen atoms. Clusters (real particles) are cross-level entities that possess three modes of motion: Translation, rotation, and vibration. The planar motion of the earth can be expressed as a combined mode of rotation and vibration, and described by an orbital state function. After establishing a state equation and solving the planar case, probabilistic predictions can be made on the conditions that cause the orbit distortion and earth disaster.

Literature Review

Motion of the earth/solar system

Motion of clusters: In classical mechanics, particles are mass points with only mass but no volume. In real particle theory, clusters are sets of spatially correlated particles characterized by their mass, volume, and shape. Clusters are independent of their spatial size, e.g., galaxies, stellar systems, molecules, and atoms are all clusters. Clusters are independent of the number of internal particles, e.g., the solar system is a multi-body cluster and the earth/solar system is a two-body cluster.

The curvilinear motion of a mass point includes three modes: Real translation, pseudo rotation, and pseudo vibration. The motion of a cluster includes three modes: Real translation, real rotation, and real vibration. The real translation of a mass point is the spatial displacement of the point, the pseudo rotation is the rotation of the point around the center of curvature, and the pseudo vibration is the change in curvature radius during the rotation process. The real translation of a cluster is the displacement of its barycenter, the real rotation is the sum of pseudo rotations of the particles inside the cluster, and the real vibration is the superposition of pseudo vibrations of the particles inside the cluster. The prototype of a cluster is an elastic object in the real world. The real rotation of an elastic object is called a self-rotation (spin), and the real vibration is called a self-vibration.

Elliptical orbit: The earth’s orbit around the sun is an ellipse. The ellipse equation can be expressed in polar coordinates (ρ, θ) as [8]

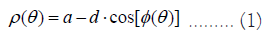
Where a is the ellipse semi-major axis, d = ae is the focal length, e is the eccentricity, and φ is the eccentrical angle. The relationship between φ and θ is

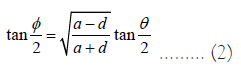
The instantaneous angular speeds of φ and θ are not equal 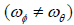. If the rotation period T is taken as the time unit, then their average angular speeds are equal 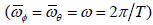. In the ellipse equation (1), the first term represents an ideal rotor with a radius a , and the second term represents a vibrator with an amplitude d .

For the earth/sun system, the earth and the sun rotate around their common barycenter in their own elliptical orbits. If the earth has rotation energy K₁ and vibration energy H₁, and the sun has rotation energy K₀ and vibration energy H₀ , then, the two-body cluster has a self-rotation energy K = K₁ + K₀ and a selfvibration energy H = H₁ + H₀ .

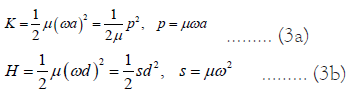
Where 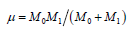is the reduced mass of the earth/sun system, p is the self-rotation momentum, and s is the stiffness. In this case, the system has a potential energy V = H − K , hence, the self-vibration energy H = K +V is the Hamiltonian of the system.

Distorted orbits: The earth’s orbit will be distorted by the approach of other celestial bodies including the moon, planets, and invasive bodies. Nearby bodies mainly affect the vibration mode of the earth. By introducing the distortion factor m and setting φ = mθ = mωt , the relationship between the polar radius ρ and the time t can be expressed by a distorted orbit equation as

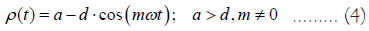
This equation excludes the circular orbit with m = 0 , but includes the elliptical orbit with m =1. Let a/d = 5 , Figure 1 shows six examples of orbits with m being an integer, in which the elliptical orbit with m =1 is called the ground state and the distorted orbits with m >1 is called excited states.

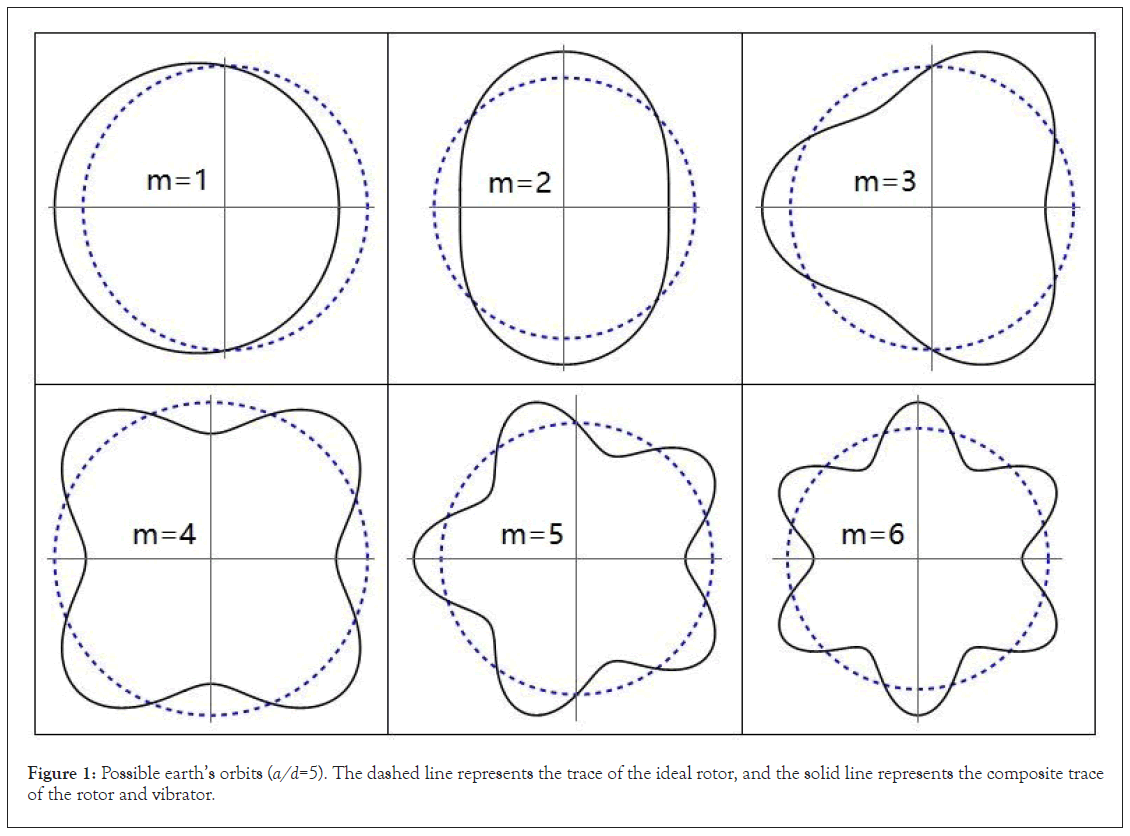
Figure 1: Possible earth’s orbits (a/d=5). The dashed line represents the trace of the ideal rotor, and the solid line represents the composite trace of the rotor and vibrator.

Mathematically, m may be any rational number, however, we want to know which values of m are allowed in physics. As the angle relationship (2) is valid only for the ground state, the instantaneous speed of the earth at excited states cannot be determined theoretically. Then, how to find more information from the distorted orbit equation?

Quantization of the Earth’s orbit

Orbital state function: The shapes of distorted orbits remind people of the hypothesis of electronic standing waves in atoms [10]. According to their similarity, the real particle theory reveals a relationship between the classical orbit equation and the quantum state function.

In real particle theory, any physical quantity q is expressed in a real quantity form is called a digit (i.e., value) and q_s is called a scale (i.e., unit). Taking the space scale r_s , the time scale t_s , and the angular momentum scale h_s , there are derived scales The related physical quantities can be expressed by

Therefore, the distorted orbit equation can be rewritten in a scale-free form

Mapping the left side of the scale-free equation to the complex plane and expressing it with a complex function Ψ , we have

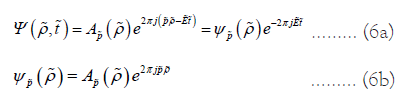
Where Ψ is called an orbital state function, ψ is called a stationary state function, and A is called a probability amplitude. The mapping relation from the distorted orbit equation (5) to the orbital state function (6) is

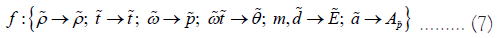
This non-one-to-one mapping cannot be expressed as a functional relation.

Because 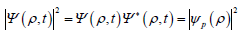does not depend on time, so it expresses an effect of temporal average. If 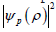is integrable in the whole space, then there is a distribution function

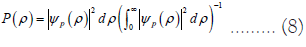
P(ρ ) represents a probability that the earth appears between ρ →ρ + dρ . This is the statistical significance of the orbital state function.

Orbital state equation: The orbital state function represented by real quantities is

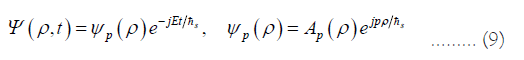
Where 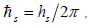The orbital state function and the quantum state function have the same form. According to the operator method of quantum mechanics, the differential equation satisfied by the stationary function can be obtained as [9,10].

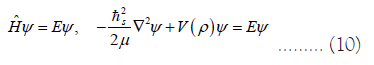
The scale h_s in the state equation is a system constant, rather than a universal constant. The atomic systems adopt the Planck constant 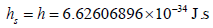. For ease of calculation, the solar system can use the earth’s angular momentum as the unit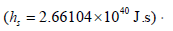

Quantized orbits: Both hydrogen atom and the earth/solar system are clusters with one particle outside the core, and their energy eigenequation is

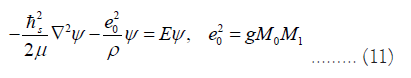
According to the general theory of quantum mechanics, the eigenfunctions of binary clusters are [10]

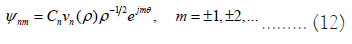
Where n is the principal quantum number and m is the distortion factor. The energy eigenvalues are

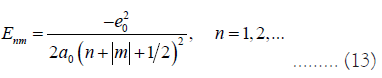
Where 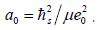Because n and m can only be integers, the energy of earth’s orbit is quantized with discontinuous levels. If the orbit jumps between the ground state and an excited state, it will result in serious earth disasters.

Discussion

Essence of matter waves

In 1924, de Broglie proposed the matter wave hypothesis to explain the quantization condition of Bohr’s atomic orbits. Shortly thereafter, Schrödinger proposed the famous quantum wave equation based on the concept of matter waves. For one hundred years, quantum mechanics has made tremendous achievements, but the explanation of matter waves has been trapped in the binary paradox of wave-particle duality. This study tells people that the essence of matter waves is the mass vibration of clusters. Because the polar angle θ is not equal to the eccentrical angle φ , the cluster’s vibration makes it impossible theoretically to determine the instantaneous speed of object when the orbital period T is taken as the time unit. Therefore, using state function for probabilistic description is a supplement and transcendence to classical orbital mechanics. The real-particle field theory proves that the medium for transmitting mass vibrations is an electronic gas ubiquitously in the universe with an average density as high as 10²⁴ per cubic meter [3].

Similarity of physical laws: Real particle theory strictly distinguishes physical quantities from mathematical quantities. Physical quantity is measurable, so it can be expressed in the form of real quantity 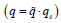. The scale q_s is a measurement unit defined as a finite variable 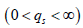. The variability of scales brings great convenience to physical operation. If there is a functional relation z = f (x, y) for any physical quantities{x, y, z}, then, there must be the following equivalence formula

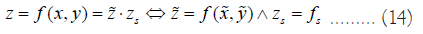
The above formula reflects the similarity of physical laws, in which 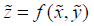is called a relation invariance and 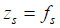is called a scale covariance. The scale-free equation (5) is an application of the similarity principle, which shows that the orbital motion satisfies a unified physical law, regardless of the spatial size and temporal cycle.

The state function is not a physical quantity and cannot be expressed by a real quantity. However, its normalized modular square can be interpreted as probability, which is a time-average effect within the orbital period.

Nature of quantum: The finiteness of scales indicate that any physical quantity contains a non-zero factor as the smallest unit. The scales vary with clusters in different levels, and satisfy the covariance condition. The covariance limits the number of independent scales to three, from which all other scales can be derived. As the unit of measurement, the concept of scale encompasses the semantics of quantum. The real particle theory shows that the actual entity represented by scale or quantum is the cluster, rather than individual particles. The particle-like behavior of quantum comes from cluster’s translation mode, the wave-like behavior comes from the vibration mode, and the spin property comes from the rotation mode. Quantum mechanics is essentially a statistical theory of cluster kinematics.

Conclusion

The planar orbital motion of the earth/solar cluster includes rotational and vibrational modes, and the changes in vibration mode result in orbital distortion. The distorted orbit equation can be mapped onto the complex plane to form an orbital state function which satisfies the quantum wave equation. The quantization of distorted orbits shows that the extra-terrestrial disturbances may cause the earth’s orbital jump and biological extinction. The relationship between orbital state function and quantum state function provides a realistic interpretation of quantum mechanics and paves the way for the unification of physics theories.

Acknowledgement

The authors thanks Professor Xie LH for his useful discussion.

Conflicts of Interest

The authors declare no conflicts of interest.

References

1. Liang ZC. Outline of real physics. Glob J Sci Front Res A. 2020;20(3):9-27.

   [Crossref] [Google Scholar]

2. Liang ZC. Modeling of real particles. J Phys Conf Ser. 2019;1391:012026(1-18).

   [Crossref] [Google Scholar]

3. Liang ZC. Dark matter and real-particle field theory. Glob J Sci Front Res A. 2021;21(6):27-39.

   [Crossref] [Google Scholar]

4. Liang ZC. The origin of gravitation and electromagnetism. Theor Phys. 2019;4(2):85-102.

   [Crossref] [Google Scholar]

5. Liang ZC. Motion, energy and state of body particle system. Theor Phys. 2019;4(2):66-84.

   [Crossref] [Google Scholar]

6. Liang ZC. Motion of elastic particles and spectrum of hydrogen atoms. Glob J Sci Front Res F. 2019;19(4):19-28.

   [Crossref] [Google Scholar]

7. Liang ZC. Cluster ensemble statistics of body particle system. New Horiz Math Phys. 2019;3:53-73.

   [Crossref] [Google Scholar]

8. Liang ZC, Xie LH. Wave or Particle? Quantum behavior of solar system. Res Square Preprint. 2023.

   [Crossref] [Google Scholar]

9. Liang ZC. The paradigm shifts of particle theories: Exemplars of solar and atomic systems. Res Gate Preprint.

   [Crossref] [Google Scholar]

10. Qian BC. Quantum Mechanics. Beijing: Higher Education Press. 2016;1:22(5):189-191.