G12

The use of diffusion based asset pricing theories in pricing real world financial assets presents a major challenge for economists and financial experts. Calibrating diffusions to real price data and in particular derivatives’ prices, even if we allow for stochastic volatility, has proven a particularly difficult task. One of the reasons of such difficulty in fitting real stock return and option price data to most models is that real prices seem to exhibit exposure to extreme moves (excess kurtosis) and asymmetry (skew) in ways that do not seem easy to comprehend. In such an environment an investor who exhibits skew preference can improve the mean-variance profile of an asset by “selling” its return skew either through dynamic trading or using option based strategies. Leland [1] argues that the classical beta does not account for skew and should be replaced by 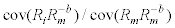with b the “market price of risk” for a power utility investor.

Evidence of jumps that help better explain the higher moments of asset returns, namely excess kurtosis and skew, is now widely recognized. Merton [2] recognized that theories developed for continuous path dynamics such as Black and Scholes option pricing will have to be modified in order to explain how risk averse agents demand to be compensated for their exposure to jump risks¹. Early theories that incorporated discontinuity and fat tails in price dynamics mainly focused on the implications of exposure to significant events (so called “peso” moments); that is large but infrequent jumps that are clearly identified breaks in the price process. Even though such jump diffusion models can correctly incorporate extreme events at a macroeconomic level, their assumed low jump activity cannot suitably capture discontinuity of a more frequent and continuously present nature. To counter this, the asset pricing literature has shifted its attention to the implications of a different type of jump risk exposure; small jumps that arrive intraday at a potentially very high arrival frequency are now commonly used.

Related to the approach of jointly incorporating jumps and diffusive volatility (in an effort to better explain true stock dynamics) is the acceptance of the fact that not all price volatility is due to changing fundamentals but also due to trading alone. Even though everybody agrees that stock prices encapsulate publicly available information about the state of the company, some of the volatility in stock prices seems to be due to noise trades rather than due to new information [3]. Since the real life econometrician is only endowed with discrete observations, recognizing jumps that occur in continuous-time becomes more difficult if the jump sizes are of a potentially small size, because they could be in principle attributed to a mixed jump-diffusion process that also includes micro-structure noise. Knowledge of a stock’s jump loadings (i.e. its sensitivity to jumps) can enhance financial risk management. The problem is that assuming that we can observe the market jump component processes separately is unrealistic; in most cases we observe only the total market return in discrete times. Below, I review two methodologies of estimating jump betas a) the more widely used high frequency procedures, and b) a simple skew-based methodology.

In recent years, due to advances in information technology, we have witnessed the move away from a manned trading floor towards completely electronic trading largely devoid of human intervention (Straight-through processing). This move has generated the availability of databases consisting of observations sampled at ultra-high frequency up to every second, and thus facilitated an extensive research program² that takes advantage of high frequency data. When the econometrician is endowed with ultra-high frequency data, it is tempting to try to isolate the jumps as moves greater than a specific value (say 1%). In a significant contribution to the literature Barndorff-Nielsen and Shephard [4,5] study two natural measures of the realized within-day price variance, the well known day (t) Realized Variance that measures the summed quadratic log-returns 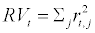and the novel realized Bipower Variation that measures summed neighboring log return cross-products 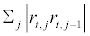. Time is measured in daily units for integer t, and for an N partition of the t^th day, we denote the within-day logreturns r_t,j=p_t–1+j/N– p_{t–1+(j–1)/N}. The significant and intuitive finding is that, under reasonable assumptions about the stock price dynamics, when the fineness of the partition tends to infinity, the two measures have different limits, with lim_N→∞ RV_t and lim_N→∞ BVt respectively including and not including jump activity. This allows us to quantify jump activity through the difference between the two measures.

The High and Ultra-High Frequency methods are promising and are quite attractive among researchers and practitioners. Yet, and despite their attractiveness, there are many practical issues related to their implementation that limit our ability to calibrate them to real data and challenge their true practicality and robustness: a) The most important problem is that usually High Frequency methods don’t retain power when applied to the noisy high frequency data. B) When applying High and Ultra-High Frequency methods, one has to determine the rejection regions for claiming jump arrivals; i.e. determine the cut-off value that constitutes a jump move. For example, will this value be 1% or 1.2%? This is a difficult question to answer without first imposing some restrictive (and potentially unjustified) assumption about the underlying distributions for the noise variance, the underlying return process volatility, the jump arrival intensity, and the distribution of jump sizes. Even when jumps are detected in a particular period (say 15 min) one cannot reasonably assume that the entire price move is due to the jump. That means that even when we are relatively confident a jump has occurred, we still need to decide what part of the return constitutes the jump and what part is due to the ever present diffusive noise. One faces the dilemma of how fast to sample the TAQ database. One can seemingly increase the power of tests by increasing the frequency of observations over a fixed time interval. Faster sampling (say at 5 min intervals) allows for easier jump detection but at the same time increases the noise due to market microstructure and in particular the so called bid-ask bounce. Slower sampling (at say 30 min intervals) takes care of a large part of the market microstructure noise but increases the need to make unjustified parametric assumptions about the underlying jump sizes’ distribution, intensity of arrival and so on.

In this section we present some ideas behind the method developed in Polimenis [6] that does not rely on high frequency data and is thus immune to market microstructure effects. According to that paper the cumulative effects of same-sign market wide jump activity during the investing period should be understood as unobservable information factors (i-factors) for the market. The loadings of individual stocks to these factors quantify exposure to significant market risks and constitute a set of new risk measures that aim at filtering away trading noise from information arrival. According to this concept, noise evolution occurs in continuous time along a continuous price path, while new information arrival that fundamentally alters the state of the market is recorded via price jumps. So unlike most literature, this framework has the following 3 basic tenants:

• Noise is the diffusive part of stock returns and not necessarily their idiosyncratic component,

• All information, systematic and stock specific, “travels” via jumps,

• Systematic information travels via market wide jumps,

• stock specific information is recorded at idiosyncratic jump times,

• Individual stocks have a varying degree of (possibly) asymmetric exposure to new information.

Under such a model, we may think of the market move during a period dt as decomposed into a continuous Brownian systematic noise component w(dt), with variance 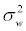, and a discontinuous informational jump component j(dt)

Δm(dt) = a_mdt + j(dt) + w(dt)

Even though formal details are left out of this paper, mathematically, we are always allowed to think in such terms due to the famous Ito decomposition of a Levy process [7]. Furthermore, as shown in the 3^rd hypothesis above, it is natural to allow stock log-returns Δp to have differential loadings on the (diffuse) noise versus the information (jump) market moves, and further recognize that stocks usually tend to exhibit asymmetric loadings on negative versus positive news with the total market jump being decomposed into its positive and negative components

j(dt) = y(dt) – z(dt)

The model for the ith stock return then becomes

Δp_i(dt) = a_idt + β_iw(dt) + γ_iy(dt) – δ_iz(dt) + e_i(dt)

with β the individual stock loading on the diffuse market noise, and the idiosyncratic stock specific noise

e_i(dt) = q_iw_i(dt)

In this setup, total stock variance (energy) 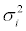is decomposed into the diffuse systematic variance (noise) 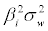, the systematic jump variance (signal) 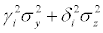and the idiosyncratic (again noise) variance .

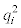The problem in identifying the jump loadings is that assuming that we can observe the Y and Z processes separately is unrealistic; in most cases we observe only the full market return in discrete times. The main idea in Polimenis [6] is the development of a set of universal coskew conditions that can be used to quantify the degree of exposure of individual stocks to the latent jump risk factors. Skew and co-skew are high order cumulants and “blind” to Gaussian noise, whereas covariance based statistics are not. For example, the classical beta 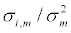of running a regression of Δp against market returns Δm wrongly assumes a single factor risk, and depends only on the breakdown of the total quadratic variation into its individual components and thus does not carry path specific jump information

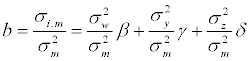
On the other hand the noise parameters do not participate in the co-skew of Δp to Δm

σ_imm = γ_iς_y – δ_iς_z

Consequently, skew-based methods improve the “signal-to-noise” ratio of our estimates. The paper uses this idea to develop a nonparametric set of skew conditions that can be used to help identify the magnitude of the latent jump components, and furthermore, the degree of exposure of individual stocks (the loadings) to such risks. According to Polimenis (2012), once we view the Gaussian part of the price path as noise, we need to shift our attention to skew rather than variance as the most significant moment.

Skew and co-skew estimates are quite sensitive to extreme realized values, and the robustness of the technique is further investigated in Theodosiadou, et al. [8]. More recently Polimenis and Papantonis [9] extend the methodology and propose to make it more robust through the estimation of the jump betas for two stocks jointly. They observe that the requirement that the individual stock skew is exactly matched is placing a burden on the estimation system, and argue that when this restrictive requirement is relaxed in a joint framework the system calibrates to more robust solution revealing information about the level of idiosyncratic skews. Under this system the idiosyncratic component becomes

e_i(dt) = u_i(dt) + q_iw_i(dt)

where u_i(dt) ~ (0, dt) is the pure jump idiosyncratic info. Allowing for stock jumps that are not simple transmission of market jumps but directly related to the underlying stock is a realistic assumption.

Measuring a stock’s exposure to jumps is important for financial risk management and portfolio construction. This is a fascinating and technically challenging area of ongoing research. The purpose of this short review paper is to stimulate a debate as to the potential merits of the high frequency methods on one hand and the skew based frequency neutral methods on the other hand. Due to the limited space, only a few papers focused on jump and jump-beta estimation are discussed, so the paper does not in any way claim to be a thorough review paper.

¹See for example Pan [10], Eraker [11] and references therein.

²Huang and Tauchen [12], Jiang and Oomen [13], Lee and Mykland [14], Todorov and Bollerslev [15], Lee and Hannig [16], Lee [17].