76.80.+y; 33.40.-e; 71.38.+1; 03.40.kf

Biological experiments show that there are a great number of electrons or charges transfer in the biological tissues and processes, such as the mitochondria, chloroplasts and chromatophores, the conduction of the nerve impulse, etc. [1,2]. As known, within the mitochondria a series of chemical transformations, called the citric acid (or Krebs) cycle, breaks down the carbon chain of glucose to carbon dioxide and produces nicotamide adenine dinucleotide (NAD⁺) plus a proton (H⁺) and two electrons (2e^-). These two electrons make three trips across a region off intrinsic membrane protein, carrying two protons inside the mitochondrion to outside on each pass. The dynamics of the two electrons (2e^-) through the region of intrinsic membrane protein is of primary interest. This phenomenon shows that there is really an electron or proton transfer chains in the mitochondria, which are combined in a highly organized complex of protein molecules, the latter form the part of membrane of mitochondria. As a matter of fact, the process of the electron transfer occurs along the respiratory chain in its inner membranes of the mitochondria. The electron transfer can be carried out through different mechanisms and forms, such as the tunneling transfer of electrons and the electron transport over large distances in virtue of protein molecules [3-5]. However, there are always the donors and acceptors of the electrons and their carriers in the transfer process of large distances in virtue of protein molecules. In this model the electrons are transferred by the exciton or soliton in protein molecules, i.e., when the exciton is formed as soliton through deformation of chain, then electrons in donors are also attached on the soliton through the interaction between the donor and soliton and move further following the motion of the soliton along the molecular chains. Once the soliton meets and acts with the acceptors, the electrons are transferred to the acceptors from the soliton and attached on the surface of the acceptor. This process can be represented by

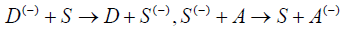(1)

Therefore, the electron transfer is, in essence, a process of oxidation-reduction reaction. In this process the protein molecules play the bridge role of transferring the electrons in the life bodies.

Many scientists studied the electron transfer in different systems using different methods [6-9], for example, Davydov et al studied the electron and excitons in nonlinear molecular chains by a soliton theory [6], Sataric and Zakula; Sataric et al. [7,8] studied the electron transfer along the quasi-one-dimensional molecular structure by Davydov soliton model, Goldman [9] studied the long-range electron transfer in protein by a renormalized-perturbation-expansion approach. In this paper we will study the properties of the electron transfer in the protein molecules by Pang’s soliton model [10-33], in which we think the electron transfer in protein molecules is carried out in virtue of the following mechanism. When the soliton is formed in the protein molecules with finite temperature under action of energy released in ATP hydrolysis, the deformation of the protein molecules occurs, then the electrons can be adhered on the soliton through an attracted interaction between them and moves towards the acceptor to accompany the motion of the soliton along the protein molecular chains. When they approach the acceptors, the electrons are transported to the acceptors due to the interaction between the electrons and acceptors. Thus the electrons are transferred to the acceptors from the donors in virtue of the soliton. Our studies are described as follows.

The Hamiltonian and wave function of the system and its soliton solution of dynamical equation

Based on the above mechanism of the electron transfer in protein molecules proposed by us we can give the Hamiltonian of the great system, which is composed of protein molecules, donor, acceptor and electron, in Pang’s model [9-33], which is as follows:

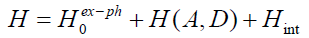(2)

Where

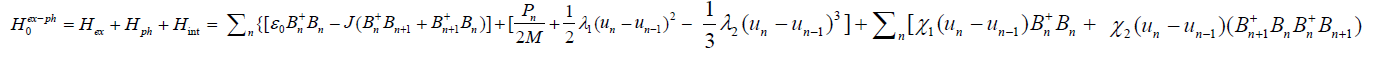(3)

It describes the motions of the exciton and phonon and their interaction in Pang’s model. The Hamiltonian of the donor and acceptor is denoted as:

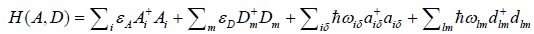(4)

Where 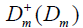and 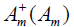are the creative and annihilation operator of the electron in the donor with the energy ε_A and the electron in the acceptor with the energy of ε_A, respectively. 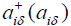and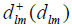 the creative and annihilation operator of the Boson in the donor with the energy 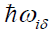and the electron in the acceptor with the energy of 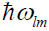arising from the excitation of vibration, respectively.

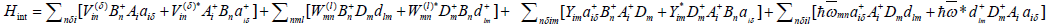(5)

Where 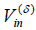is the matrix element of interaction between the exciton and vibrational excitation (l) of the acceptor at site i, l is the matrix element of interaction between the exciton and vibrational excitation (l) of the donor at site m, they have a maximum when,

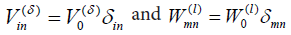(6)

Y_im is the matrix element of interaction between the exciton and electron in the electron migration from the donor to acceptor.

As it is known, there are still the coherent features of collective excitations of the exciton and phonon arising from the energy released in ATP hydrolysis in the protein molecules, although the donors and acceptors exist in this system, which are very small. Thus the wave function of the system containing small donors, acceptors and electrons can still be represented by:

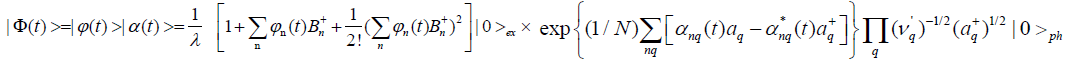(7)

Where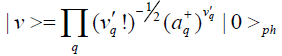

Is the phononic complete set which represents the elementary excitation state of single phonon due to the finite temperature T ≠ 0. In this meanwhile, we here used the following relations:

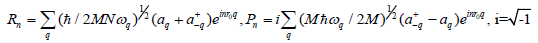(8)

where ωq=2(W/M) ^1/2 sin(r₀q/2) is the frequency of a phonon with wave vector q, N is the number of amino acid in the molecular chain, r₀ is the distance between two amino acids, 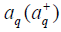is the annihilation (creation) operators of phonon.

From equations (2)-(6) and 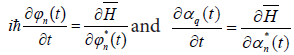(here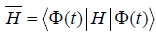 ). In continuity approximation and in one dimensional case [6-12] we can obtain:

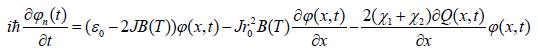(9)

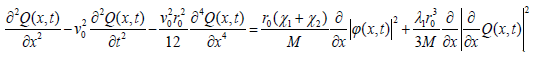(10)

Where ,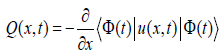

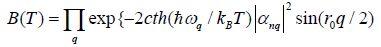
Using an approximate method we can obtain the solutions of equations (8 and 9) as follows:

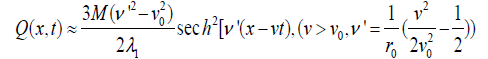(11)

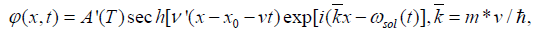(12)

Where 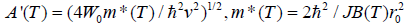. We can find out the solutions of Eqs. (8 and 9) in the case of in initial condition of 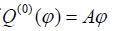using the iterative method [6-12], which can be represented by:

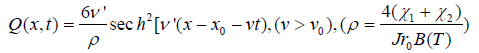(13)

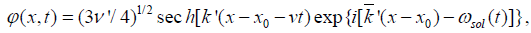(14)

Where 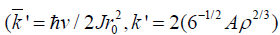. Clearly, the above soliton solutions in equations (12) and (14) are the supersound solitons and stable, which thus can serve as the carrier of the electron transfer in living systems.

The dynamical coefficient of electron transfer and its properties

We now calculate ratio of the electron transfer from the donor to acceptor by virtue of the above supersound solitons. In the system of electron transfer the number operators of the soliton, donor and acceptor are denoted by:

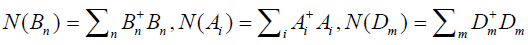respectively. Obviously, whole particle number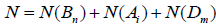, which is related to Hamiltonian of the system in Eq. (2), is conservative, i.e.,

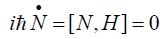
These number operators satisfy the following Haisenberg equations.

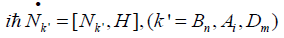(15)

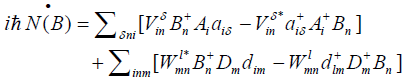
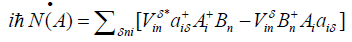
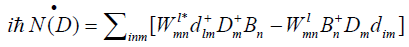(16)

In this system of electron transfer the number currents formed are in equilibrium state and satisfy the following relationship.

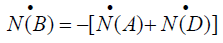(17)

Based on this feature we can use the statistic theory of quasi-equilibrium state established by Zubarev [34] to study the electron transfer. Corresponding statistic operator of the quasi-equilibrium state can be represented by:

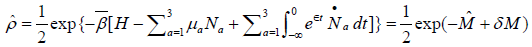(18)

Where

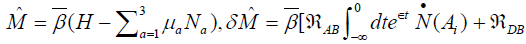
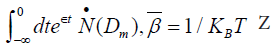is statistic sum of the system, μ_a is the chemical potential of ath component. ε is a small parameter, 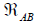and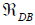 denote the chemical affinity in the chemical reaction in Eq.(1), their relationship with chemical potential are as follows:

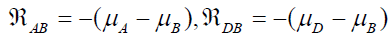(19)

Since 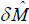is small and the request of normalization, i.e.,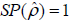, then Eq. (10) can express as:

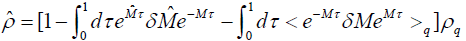(20)

where 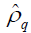is a localized equilibrium density matrix, which can be denoted by:

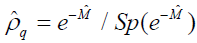(21)

Then the number current of acceptor can be expressed by 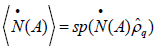, thus we yield.

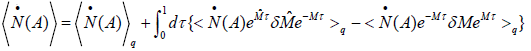(22)

There is the relation of 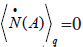in the localized equilibrium state without dissipation, then the number current of acceptor can be expressed by:

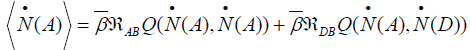(23)

Where the dynamic coefficients in this process are of the forms:

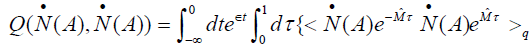(24)

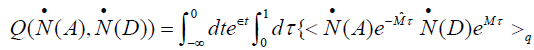(25)

These coefficients characterize the sizes of change of particles and features of particle current formed, respectively. They represent the number of particles of transformation in unit time in the process of electron transfer. If the quadric terms in Eq.(2) are only considered, the operator 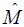can represent as

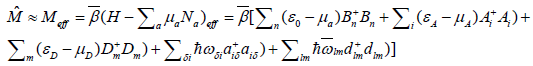(26)

Utilizing Eq. (26) and separating the functions related to τ and completing these integrations in it then we denote Eq. (24) as:

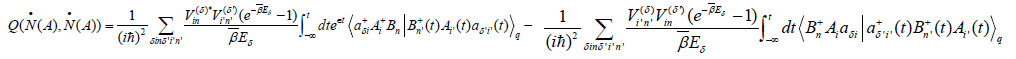(27)

Where we used the following relationships:

,

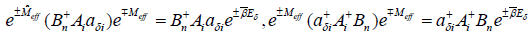
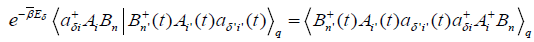
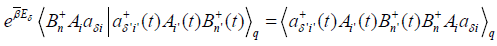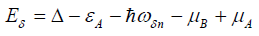
These dynamical coefficients can become the following Onsager representations in virtue of Boson postponed Green function [6-7,34].

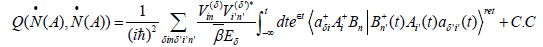(28)

where

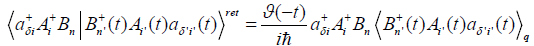
where the step function .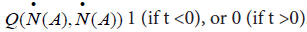

Because the dynamical coefficient 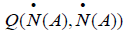contains odd Fermi operators, thus its average is zero.

In order to find out the explicit representation of 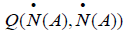we must calculate the Green function of three particles as above mentioned. We here denote approximately it by Green function of signal particle. Since H(A,D) is only related to squares of A_i and a_δi, then the following equations hold.

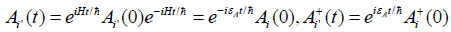
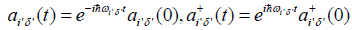
Utilizing these relationships, then Equation (28) can be expressed by the Green function of signal particle for the Boson operator B_n of the exciton, which is as follows:

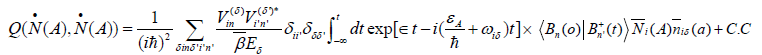(29)

Where .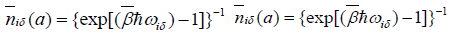

We now study the roles of the above supersound soliton in the process of electron transfer. In this case, let the above Green function denotes as:

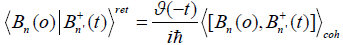
For the coherent wave function in Eq.(7) the Boson operator B_n(t) has the feature.

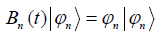
Applying these features and Wojtezak’s method [35] and further considering the influence of temperature of the system, then the Green function of signal particle can be found out, which is:

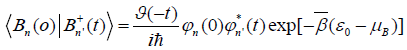
Thus, Eq. (29) can represent as:

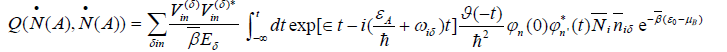
Where 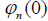amd 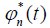are the amplitudes of the supersound soliton in Eqs. (12 and 14). Inserting Eq. (12) into Eq. (30) we can obtain.

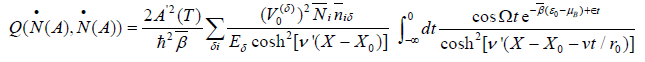
Where .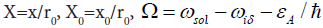

We now find out the integration of t in Eq. (31), which is:

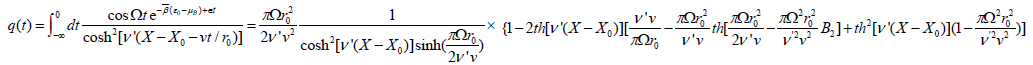
Where B₂ is Bernoolli number. Then the above dynamic coefficient can finally denote as:

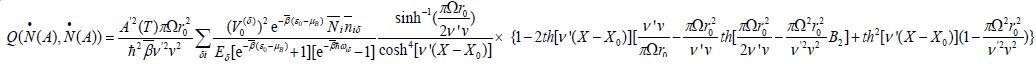(32)

Equation (32) is just the dynamical coefficient of electron transfer along the protein molecules by the supersound soliton in Eq. (10). Obviously, the speed of the electron transfer is related to the amplitude and velocity of the soliton, the electron’s distribution in the donor and acceptor as well as the interaction among the soliton, donor and acceptor. In general, the stronger the coupling between them, then the larger the speed of electron transfer because the latter is directly proportional to the square of the interaction potential 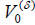. This is corresponded with practical case and reasonable. Therefore, the above result is correct. In order to exhibit clearly the features of the electron transfer we now study some special situations.

1. The features of the electron transfer in the case of higher concentration of donor and acceptor. In this case 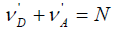. This means that 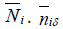and δ are not related to i, δ =1 and the sum, 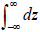, can be replaced by the integration 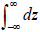. Thus we can obtain from Eq. (32)

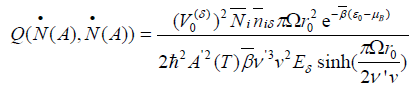(33)

This shows clearly that the dynamic coefficient is also directly proportional to the square of the interaction potential 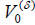and decreased with increasing the velocity and amplitude of the soliton. This means that the speed of electron transfer by larger and fast soliton is small than that by small and slow soliton in this case.

If we further take account of this case of 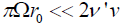, thean Eq. (32) becomes as:

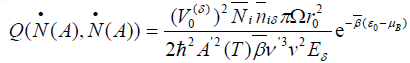(34)

Thus we know that the dynamical coefficient will increase intensely in the case 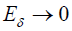and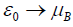

2. In the case of v = 0. This means that the supersound soliton is in static state. From Eq. (31) we can obtain:

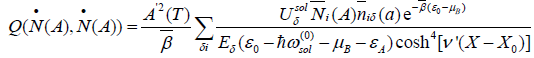(35)

Where

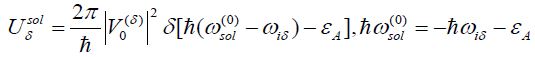
If the features of dynamic coefficients among Eqs. (31, 32 and 35) are compared we can find that the dynamic coefficient in the case of v=0 is larger than those in other cases. This resemble the electron transfer by the bell-type magnetic-soliton and the result of transfer speed of energy of ferromagnetic resonant in the ferromagnet obtained by Wojtezak and Sukiennicki [35].

Otherwise, we can also obtain the dynamic coefficient of donor, 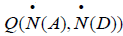, if only the parameters of the acceptor in Eqs. (31- 35) are replaced by corresponding parameters of the donor. However, to find representation of 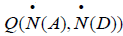is difficulty. We must again add the interaction between the acceptor and donor, which is 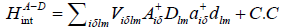, into the above Hamiltonian. Then its calculation is complicated, which is studied in other paper.

The relaxation time of the electron transfer, which denotes the size of speed of electron transfer from the donor to the acceptor, is an inverse measure of the dynamical coefficient. Thus it can be represented by 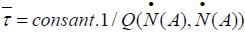. Using Eq. (35) we can obtain.

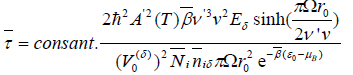(36)

Then the electric current formed in the electron transfer process in the protein molecule can be represented by:

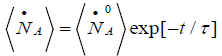(37)

This representation is very useful in molecular and chemical biology.

In this paper we studied the mechanism and properties of electron transfer along protein molecules with finite temperature T ≠ 0 in the life systems using nonlinear theory of bio-energy transport and Green function method. The mechanism of the electron transfer can be described as follows. When the supersound soliton is formed under action of energy released in ATP hydrolysis, in which deformation of protein molecules occurs, the electrons are adhered on the soliton through an attracted interaction between them and moves towards the acceptor to follow the motion of the soliton along the protein molecular chains. When they approach the acceptors, the electrons are transported to the acceptors due to the interaction between the electrons and acceptors. Thus the electrons are transferred from donors to acceptors in virtue of the supersound soliton. Therefore the mechanism of the electron transfer is, in essence, just a process of oxidation -reduction reaction. Based on this mechanism we first give the Hamiltonian and wave function of the system and find out the soliton solution of the dynamical equation in the protein molecules with finite temperature, and obtain finally the dynamical coefficient of the electron transfer and its features of transfer. The results obtained show that the speed of the electron transfer is related to the amplitude and velocity of the soliton, the electron’s distribution in the donor and acceptor as well as the interaction among the soliton, donor and acceptor. In general, the stronger the coupling between them, then the larger the speed of electron transfer because the latter is directly proportional to the square of the interaction potential 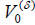. Meanwhile, we finally get the changed rule of electric current arising from the electron transfer with varying time. These results are useful in molecular and chemical biology.

The authors would like to acknowledge the National “973” project of China for financial support (Grant No: 212011CB503701).